连续波脉冲器压力波发生与优化研究

薛 亮，刘 敏，韩 虎，刘献博，王智明，张 峥，邵天宇

(1.中国石油大学(北京) 石油工程学院，北京 102249； 2.中海油田服务股份有限公司，天津 300452)

引 言

目前，随钻测量系统(MWD)被广泛应用在油田上来保证钻井质量，提高钻井效率[1-4]。连续波泥浆脉冲发生器(简称连续波脉冲器)是随钻测量系统的重要部件，主要有负脉冲发生器、正脉冲发生器和连续波脉冲发生器3种[5]，其中连续波脉冲器具有传输速率高的优点，因此得到国内学者的广泛关注。李军等[6]研究了连续波脉冲器发生原理与自适应控制；房军等[7]对连续波脉冲器结构参数影响与设计进行了大量研究；王智明等[8-11]研究了连续波脉冲器结构、工作模式并进行了循环管路试验；苏义脑[12-15]等研究了泥浆脉冲发生器信号传输速度及传输特性。以上研究对连续波脉冲器的结构优化、信号传输等具有重要价值，有效推动了连续波脉冲器的发展，但对压力波的波形特征研究则不够深入。进一步的研究发现，连续波脉冲器压力波正弦性较差，导致压力波在传播过程中衰减较快，不利于信号传输，因此有必要对压力波特征进行优化[16]。然而现有的压力波优化方法均是改善脉冲器结构，这种优化方法操作很复杂。

本文基于连续波脉冲器流场模型，利用fluent软件进行数值仿真，提出了改变转子相位角的简单优化方法，优化压力波波形与幅值特征，为连续波脉冲器理论研究与现场应用提供指导。

1 脉冲器流场数值仿真方法

物理实验过程中，连续波脉冲器流场受到柱塞泵、边界反射、软管弹性等诸多因素的叠加干扰，增加了对实验结果分析的难度。本文基于计算流体力学相关理论与方法，建立脉冲器流场数值仿真模型，可以排除实验条件的干扰，有利于深入研究压力波发生过程与特征。

1.1 连续波脉冲器结构与原理

连续波脉冲器结构复杂，主要由本体、电机、流道转换接头、接头、定子、转子、伸缩杆等结构组成(图1)。压力波发生的关键部位是定、转子，以及定转子间隙，本文研究条件下定转子间隙设定为1.23 mm。

连续波脉冲器工作原理：转子往复摆动过程中过流面积不断变化产生压力波动。转子关阀时过流面积减小，压力增大；转子开阀时过流面积增大，压力减小。控制转子连续开关阀运动，就会产生连续压力波[15]。

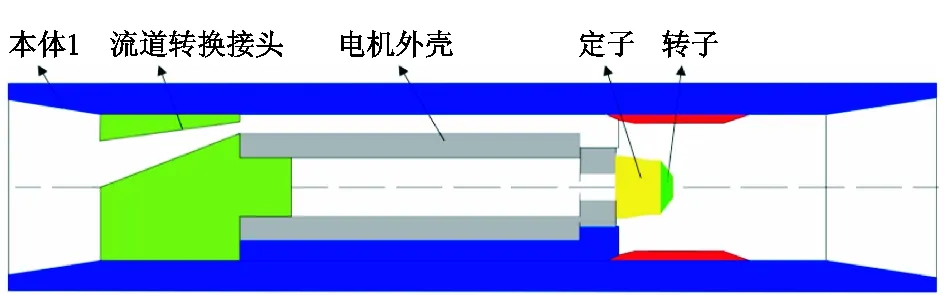
图1 连续波脉冲器剖面Fig.1 Profile of continuous wave pulser

1.2 连续波脉冲器流场与网格模型

根据连续波脉冲器机械结构模型，在机械制图软件中通过布尔运算抽取本体流道、电机流道、定子流道、转子流道以及定转子间隙流道。图2为定子流道、定转子间隙流道、转子流道等主要流道的剖面图。由于脉冲器模型各部分结构尺寸相差较大，采用统一尺寸划分网格时造成网格数量过多，因此采用网格分区技术生成结构化网格。脉冲器核心是定子流场、转子流场以及定转子间隙流场，采用加密技术生成网格，从定转子域向脉冲器模型两端划分网格时逐渐稀疏，从而降低整体网格数量，如图3所示。

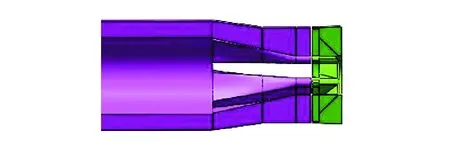
图2 定、转子及其间隙几何模型Fig.2 Geometric model of stator, rotor and gap between them

图3 定、转子域网格模型Fig.3 Grid model of stator and rotor

定子域网格57万、转子域网格30万、定转子间隙网格8万，这3部分网格合计95万。

为排除入口边界、出口边界反射影响，分别在定子上游与转子下游设置加长段，长度为1 200 m。脉冲器流场几何模型分为5段：入口加长段、定子段、间隙段、转子段、出口加长段(图4)。为了比较过流面积对压力波幅值的影响，入口加长段横截面直径设定126 mm，出口加长段横截面直径设定89 mm，两者面积比约为2。上、下游加长段网格数各50万，加在一起，网格总数为195万。在确定该网格特征时，曾对比多种网格分布对流场计算精度的影响，最后发现当网格达到上述的分布特征时，流场物理量基本不再变化，故采用本文的网格模型，可以满足计算精度对网格的要求。

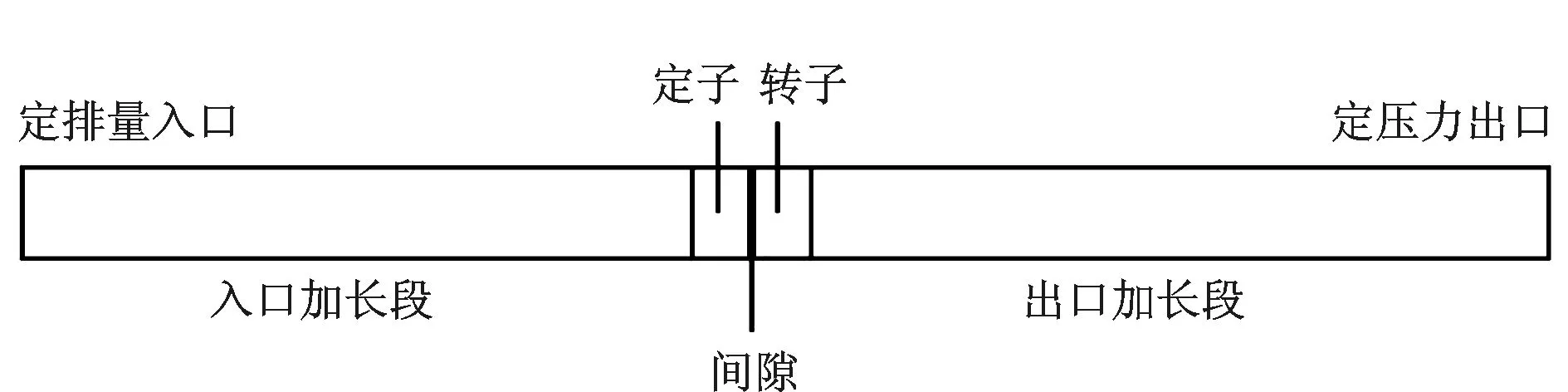
图4 流场几何示意图Fig.4 Geometric diagram of flow field

1.3 流体力学方程与边界条件

连续波脉冲器以清水为介质，转子角速度随时间以正弦形式往复摆动，可以通过三维、非定常、可压缩、湍流流体力学方程组进行描述，具体包括：质量守恒方程、动量方程、能量方程、湍动能方程、湍流耗散率方程、液体状态方程，详见参考文献[17]。

边界条件包括入口边界条件、出口边界条件、壁面边界条件、转子运动边界条件。入口边界采用无穷远定质量入口，可以排除柱塞泵产生的流量波动。出口边界条件采用无穷远定压力出口，出口表压设为0。壁面边界条件中除了转子壁面外，其他固体壁面采用无滑移壁面边界条件。转子运动边界条件采用运动壁面边界条件，编写转子运动角速度方程的UDF子程序，从而实现转子按设计方式往复运动。

2 压力波发生原理与波形特征

2.1 转子正弦转动相位角分析

连续波脉冲器定、转子结构截面示意图如图5所示。定、转子叶片均为37°扇面，开口均为23°。初始相位角是转子开始摆动时的相位角，初始相位角为0°时相当于定、转子之间的流道处于全打开状态。终止相位角为转子单向摆动设定的最大相位角，终止相位角设置为23°时，定、转子之间的流道刚好处于全关闭状态。转子终止相位角大于23°时，定、转子之间的流道处于过关闭状态。终止相位角为30°时，转子叶片中心线与定子开口中心线重合，定、转子位置完全对称。一般来说， 连续波脉冲器定、转子之间必然存在间隙，本文研究条件下定、转子间隙设置1.23 mm，由于间隙过流的存在，即使转子处于所谓的全关状态，还是有流体经过定、转子结构。定、转子间隙对压力波幅值大小有重要影响，具体影响可以参考文献[18]。

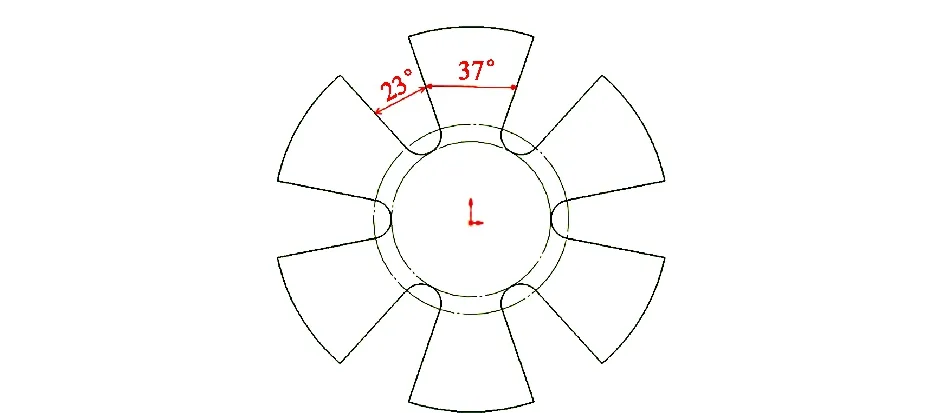
图5 定转子截面示意图Fig.5 Sectional diagram of stator and rotor

基于连续波脉冲器数值仿真模型，转子采用正弦运动方式，控制方程为

(1)

式中：ω为转子摆动速度，rad/s；f为转子摆动频率，Hz；φs、φe为初始、终止相位角，(°)；t为转子摆动时间，s。

一般来说，比较常见的转子初始相位角φs=0°，终止相位角φe=23°。以转子频率f=6 Hz为例分析角速度、转子相位角、定转子间流道过流面积的变化规律。在正弦运动方式下，转子角速度随时间变化的曲线如图6所示。由图6可知，转子角速度曲线是标准的正弦曲线，转子在初始相位角、终止相位角处的角速度均为0°，在中间相位角处角速度最大。

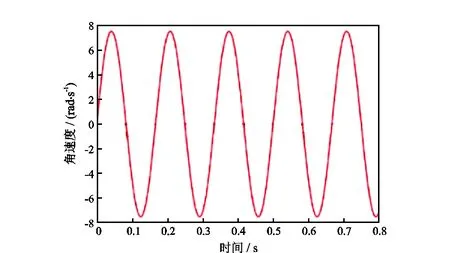
图6 转子角速度随时间的变化Fig.6 Variation of rotor angular velocity with time

在正弦角速度控制下， 得到的转子相位角随时间变化曲线和定转子过流面积随时间变化曲线也均为正弦曲线， 如图7、图8所示。由此可知， 转子在正弦运动方式下， 转子角速度曲线、相位角曲线、定转子过流面积曲线都是正弦曲线。但是， 转子在该运动方式下得到的压力波却不是标准的正弦曲线。

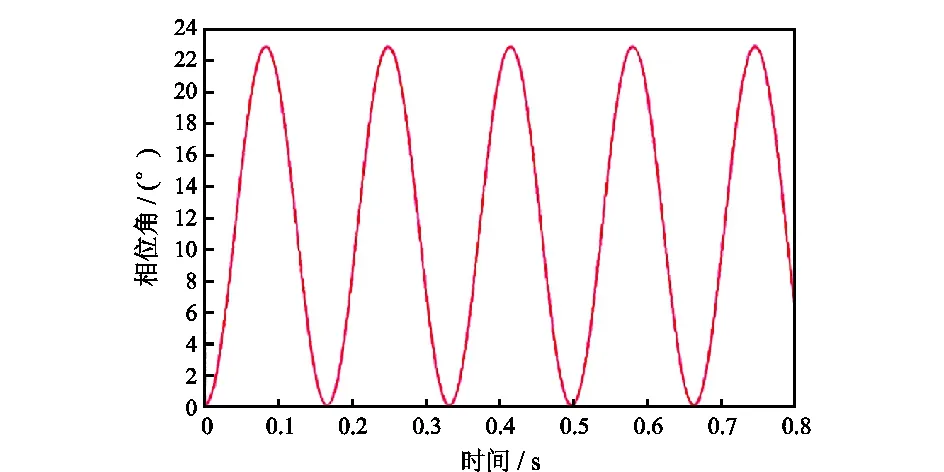
图7 转子相位角随时间的变化Fig.7 Variation of rotor phase angle with time

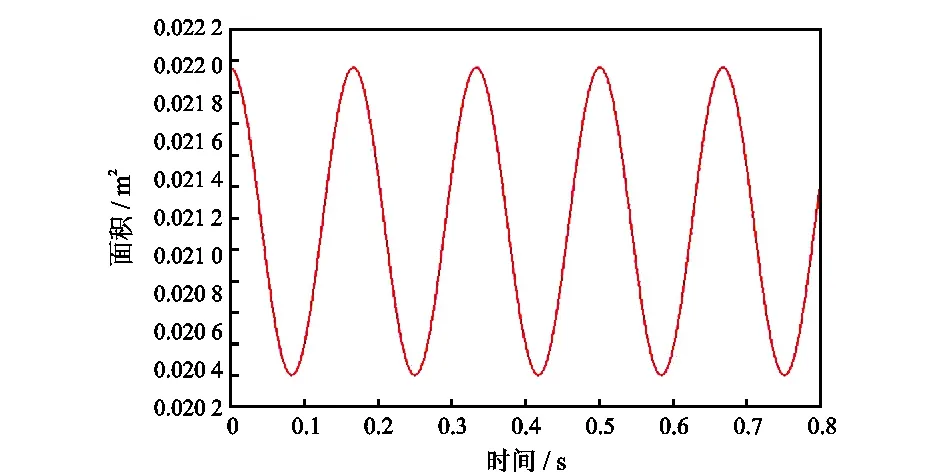
图8 过流面积随时间的变化Fig.8 Variation of discharge area with time

2.2 压力波发生原理与特征

连续波脉冲器室内实验一般采用清水介质，因此在数值仿真计算中也用清水介质，转子采用上述正弦运动形式，以及0°初始相位角和23°终止相位角，基于脉冲器流场仿真模型进行数值仿真，数值仿真参数见表1。

表1 计算参数Tab.1 Calculation parameters

脉冲器初场建立后，启动脉冲器转子往复摆动，对压力波发生过程进行数值仿真。在脉冲器上、下游各1 m位置布置监测点，监测流量、压力随时间变化数据，绘制流量随时间变化曲线(图9)，压力随时间变化曲线(图10)。从图9可以看出，在连续波脉冲器关阀过程中，转子开度逐渐减小，上、下游流量同时下降；在开阀过程中，转子开度逐渐增大，上、下游流量同时上升，随时间变化曲线完全重合。

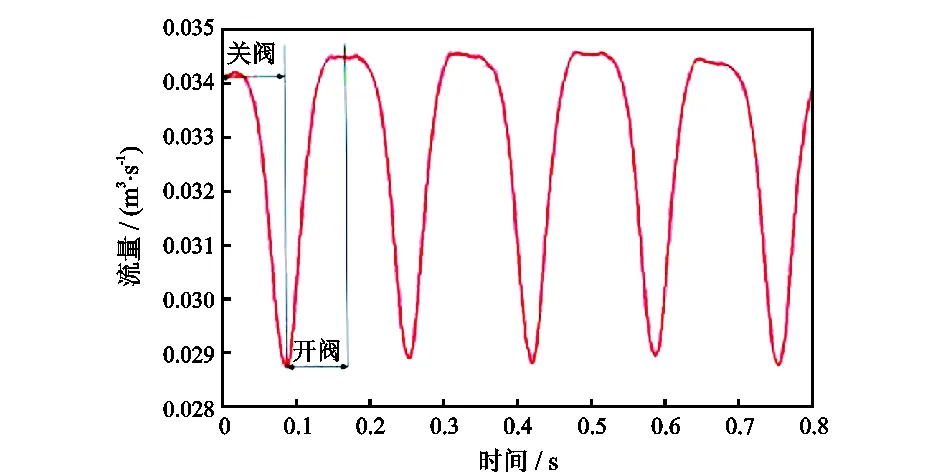
图9 上、下游流量波曲线图Fig.9 Upstream and downstream flow-rate curves

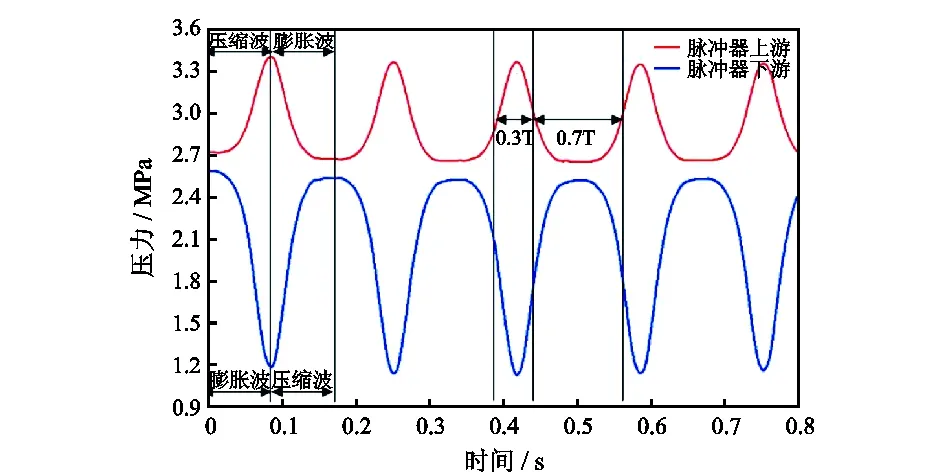
图10 转子正弦运动压力波曲线Fig.10 Sinusoidal pressure curves of rotor

关阀过程中，脉冲器位置上、下游流量下降，但是前方远场来流与后方远场流量不变，上游流体压缩产生压缩波，下游流体膨胀产生膨胀波，上、下游压力波相位相反。当转子到达全关状态时，上游压力达到最大，处于波峰位置，下游压力达到最小，处于波谷位置，如图10所示。转子摆动完成1/2周期之后，转子回摆，进入开阀过程，脉冲器位置上、下游流量上升，但是前方远场来流与后方远场流量不变，上游流体膨胀产生膨胀波，下游流体压缩产生压缩波，上、下游压力波相位相反。当转子到达全开状态时，上游压力达到最小，处于波谷位置，下游压力达到最大，处于波峰位置。

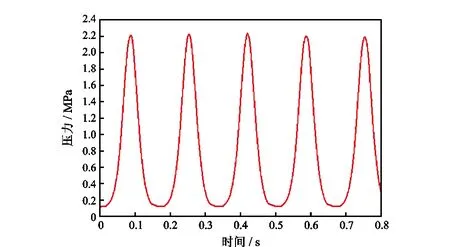
图11 上、下游压差变化曲线Fig.11 Variation curve of pressure difference between upstream and downstream

脉冲器转子连续转动，上、下游分别产生连续的压力波向上、下游传播。上游压力波幅值为0.72 MPa，下游压力波幅值为1.4 MPa，是上游幅值的2倍。这是由于脉冲器上游流道截面积是下游流道截面积的2倍，说明压力波幅值与流道截面积成反比。

图10中的脉冲器上、下游压力波曲线相减可以得到脉冲器上、下游压差曲线，如图11所示。图11表征了脉冲器随转子开度变化的压降特征，而且是流量波动条件下压降随转子开度变化的特征。由此可见，脉冲器压降曲线与上、下游压力波相关，但与压力波是两个不同的概念。

进一步分析可以发现，图10中的压力波曲线并不是期待的正弦波，其正弦性很差，压力波平衡位置时间占比为0.3T∶0.7T，半周期时间分布不均匀。说明压力与过流面积不成正比，在大过流面积(0°相位角附近)压力随过流面积变化较慢，在小过流面积(23°相位角附近)压力随过流面积变化较快。压力波正弦性较差，严重影响压力波传播，导致压力波在传播过程中衰减过快从而影响井下信号传播，需要对波形特征进行优化，改善压力波正弦性，使平衡位置时间占比接近0.5T∶0.5T。

3 相位角对压力波特征的影响与优化

针对连续波脉冲器压力波正弦性差的问题，可以考虑改变大过流面积、小过流面积时间占比的方式进行优化，通过增大初始相位角与终止相位角的方式来实现。

3.1 初始相位角对压力波特征的影响

转子初始相位角为0°时，定、转子之间流道处于全开状态，在0°相位角附近过流面积最大，通过增大初始相位角，可以减小大过流面积的时间占比。本节研究转子初始相位角对压力波波形与幅值特征的影响。将转子的初始相位角设定为3°、6°、9°、12°，转子终止相位角均为23°，对脉冲器流场进行数值仿真。提取计算数据，绘制不同初始相位角下连续波脉冲器上游的压力波曲线，如图12所示。

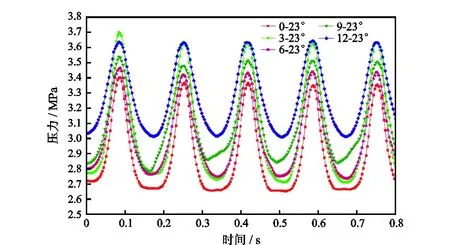
图12 不同初始相位角条件下压力波曲线Fig.12 Pressure wave curves under different initial phase angles

由图12可知，相对于转子0～23°摆角下的压力波曲线，初始相位角3°、6°、9°的压力波曲线起始压力均小幅抬高，12°的起始压力抬升较大。虽然起始压力有所抬高，但是压力波波形的半周期性却大幅改善，逐渐接近完全的正弦化。表2为压力波平衡位置时间占比与幅值统计。由表2可知，当初始相位角增加到12°时，压力波波形大幅改善，基本实现正弦化，但压力波幅值却随初始相位角的提高而下降。

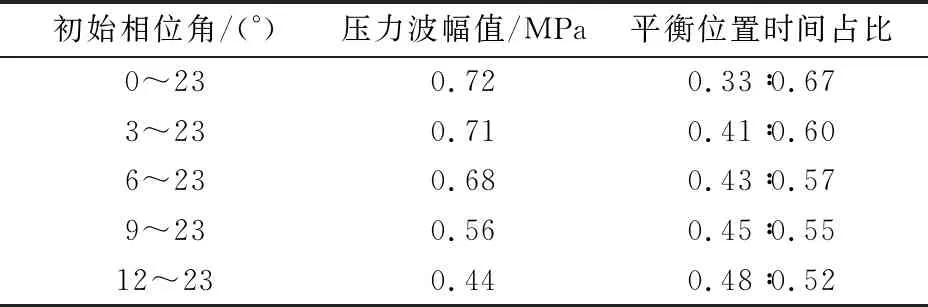
表2 不同初始相位角统计结果Tab.2 Pressure amplitude and proportion of balance position time under different initial phase angles

3.2 终止相位角对压力波特征的影响

增大初始相位角，实际是减小大过流面积时间占比，如果在大过流面积时间占比不变的前提下，增加小过流面积时间占比应该也能达到相同的效果。本节研究增大转子终止相位角对压力波波形与幅值特征的影响。上节终止相位角为23°，现将转子的终止相位角设定为24°、25°、26°、28°、30°，初始相位角为0°不变，对连续波脉冲器流场进行数值仿真。提取计算数据，绘制不同终止相位角条件下连续波脉冲器上游的压力波曲线，如图13所示。

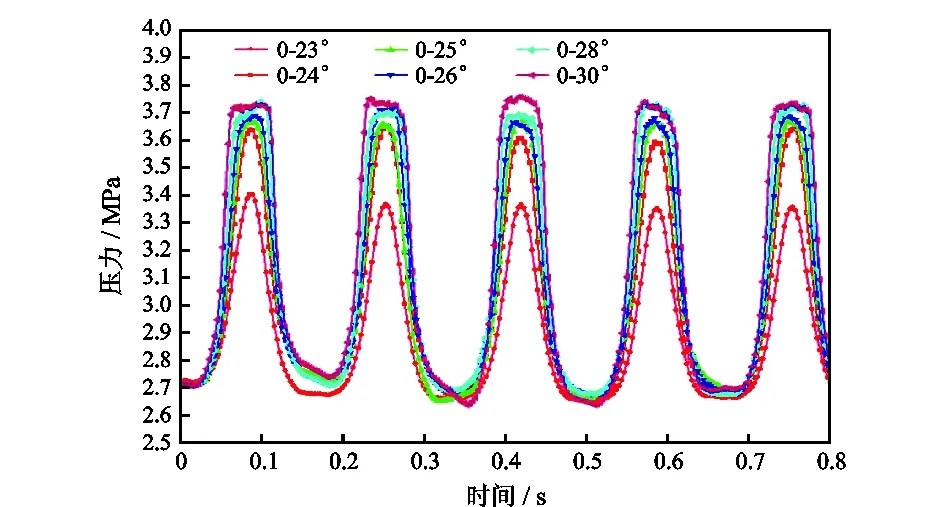
图13 不同终止相位角条件下压力波曲线Fig.13 Pressure wave curves under different termination phase angles

由图13可知，相对转子0～23°摆角下的压力波曲线，终止相位角为24°时压力波幅值大幅增大，这是因为转子摆动到23°时，尽管定、转子之间的流道刚好处于全关状态，但由于间隙的存在，大量流体通过定、转子间隙产生了绕流的影响。当转子继续摆动到24°，定、转子之间的流道处于过关状态，可以明显降低间隙绕流的影响，流量越低压力波幅值越大。增大终止相位角到25°～30°时，间隙绕流的影响进一步降低，压力波幅值继续增大但增大的幅度很小，且在波峰位置出现一个平台。图13中的平衡位置时间占比与压力波幅值特征见表3，增大终止相位角可以小幅改善压力波平衡位置时间占比，大幅提高压力波幅值。当终止相位角为30°时，压力波幅值达到最大，正弦性也得到一定程度的改善。

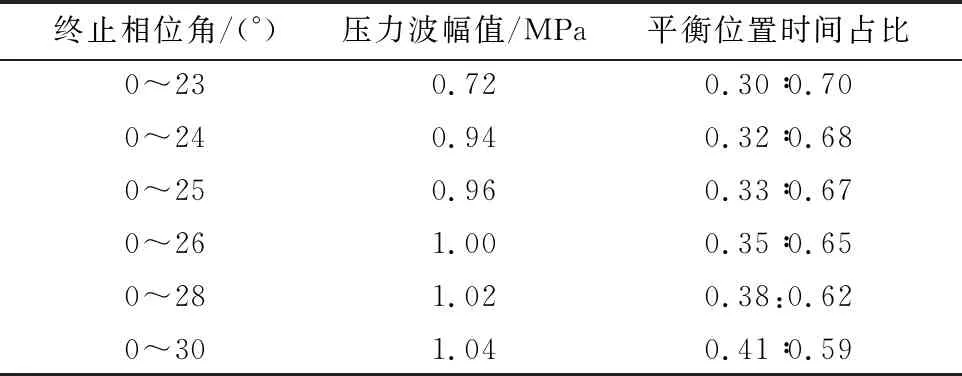
表3 不同终止相位角统计结果Tab.3 Pressure amplitude and proportion of balance position time under different termination phase angles

3.3 转子相位角对压力波的优化

转子初始相位角与终止相位角对压力波波形与幅值影响很大。增加初始相位角可以大幅改善压力波波形，降低压力波幅值。增加终止相位角可以小幅改善压力波波形，大幅提高压力波幅值。鉴于此，同时增大初始相位角与终止相位角，应该可以更好地改善压力波波形与幅值特征。由图12可知，初始相位角在12°时压力波正弦性最好，所以初始相位角选择12°。由图13可知在终止相位角为26°～30°时，压力波幅值达到最大，所以终止相位角选择26°、28°、30°。将转子的初始相位角设定为12°，终止相位角设定为26°、28°、30°，对脉冲器流场进行数值仿真。提取计算数据，绘制不同初始、终止相位角下脉冲器上游的压力波曲线，如图14所示。

图14 不同初始、终止相位角压力波曲线Fig.14 Pressure wave curves under different initial and termination phase angles

由图14可知，转子初始相位角12°，终止相位角分别为26°、28°、30° 这3种组合得到的压力波曲线差别不大，压力波正弦性都得到大幅改善，压力波幅值较转子0°～23°时都小幅增加，平衡位置时间占比与幅值统计结果见表4。其中，转子初始相位角为12°、终止相位角为28°时，半周期占比为0.49T∶0.51T，基本实现正弦化，压力波幅值为0.78 MPa，较转子0°～23°转动下压力波幅值增加8%。

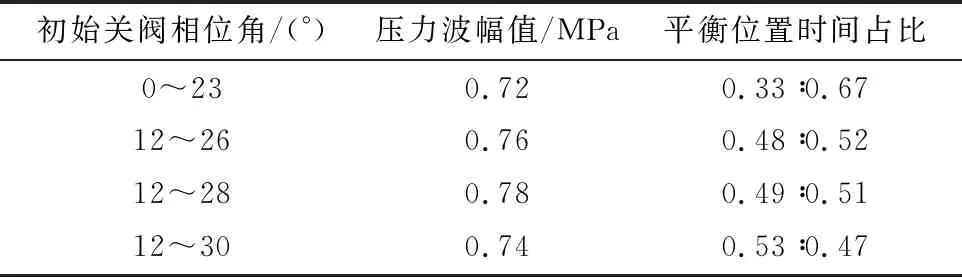
表4 不同初始、终止相位角统计结果Tab.4 Pressure amplitude and proportion of balance position time

综上所述，同时增大初始相位角与终止相位角，减小大过流面积条件下时间占比，增加小过流面积条件下时间占比，可以同时改善压力波波形与幅值特征。转子初始相位角为12°、终止相位角为28°时，压力波波形可以基本实现正弦化，有利于降低压力波信号在传输过程中的衰减程度，提高MWD信号的传输效率。

4 结 论

(1)随转子连续摆动，脉冲器上、下游分别产生连续的流量波与压力波，脉冲器压差与压力波不是一个概念，脉冲器压差是在流量波动条件下随转子开度变化的压降，具有随时间变化的周期性特征。

(2)转子初始相位角与终止相位角对压力波波形与幅值影响很大。增大初始相位角可以大幅改善波形，降低压力波幅值；增大终止相位角，可以小幅改善压力波波形，大幅提高压力波幅值。

(3)同时增大初始与终止相位角，可以同时改善压力波波形与幅值特征。在本文研究条件下，初始相位角为12°、终止相位角为28°时，压力波波形可以基本实现正弦化，压力波幅值也比较适中。