非均分流量负荷的压气站优化运行

王力勇

(中石化天然气榆济管道分公司,山东 济南 250014)

引 言

目前，关于压缩机组性能预测的研究主要有：张轩等[1-2]以固定公式结构对性能参数进行拟合，达到预测目的；李晓平等[3-8]基于相似变换原理对压缩机性能参数进行预测；刘超等[9-10]利用神经网络相关原理对压缩机组性能进行预测；郝开元等[11-12]利用商业软件建立压缩机组仿真模型，进而预测性能参数。然而，关于压缩机组性能劣化对性能参数预测的影响研究相对较少。

压缩机组优化运行的目的是在满足管线输气量的前提下，尽可能减少压缩机组的能耗[13]。熊浩云等[2-3]的研究表明直接查找压缩机性能曲线图来确定相关工作参数时误差高达约20%，因此在优化压缩机组的运行方案时，必须考虑并修正这些误差。对压缩机组实际运行数据分析得出，随着运行时间的增加，离心压缩机组的性能会有所劣化，且即使机组型号相同，劣化程度也有所区别。同时，因为实际工况与设计工况存在差异，所以直接采用出厂性能曲线来指导实际生产运行[3]，可能会导致压缩机组发生喘振或者堵塞，因此，不仅要对离心压缩机组的出厂性能曲线进行相似换算[4-7]，同时也要对性能劣化产生的误差进行修正。

本文采用相似换算原理得到实际工况下的性能数据，利用曲面拟合原理建立压缩机性能仿真模型，再导入压缩机的实时运行数据，通过最小二乘原理对性能仿真模型进行修正。在此基础上，构建压缩机组运行优化模型，以降低压缩机组总能耗。

1 性能换算与仿真

通常离心压缩机的实际运行工况与设计工况有所区别，为了获得实际工况下的性能参数值，需要利用性能换算方法对出厂性能参数值进行换算，为压缩机的性能仿真奠定数据基础。每一个转速和输量都会对应一组性能数据，因此压缩机的性能数据量十分庞大。为了便于优化压缩机组的运行方案，利用曲面拟合原理将性能数据以显性公式表示出来，进而建立压缩机的性能仿真模型。与BP神经网络等方法相比，显性公式结构的性能仿真模型在求解压缩机组运行优化数学模型时计算量更小、出错率更低。

1.1 性能换算

目前大部分离心压缩机组在运行时绝热指数相等，而特征马赫数不等，因此当压比小于2.5时，一般采用多变换算法[2]；当压比大于2.5时，压缩机组流量、功率的换算则采用半温升平均比容法[1]。

1.2 性能仿真

曲面拟合是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用曲面拟合原理可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小[14]。

利用相似换算原理求得离心压缩机组实际工况下的性能曲线，再根据曲面拟合原理[9-10]，对经过相似换算后的性能参数(功率N、压比ε)进行二元二次拟合，拟合公式为

(1)

(2)

式中：a00、a01、a02、a10、a20、a11、b00、b01、b02、b10、b20、b11均由曲面拟合原理计算得到；q为压缩机组的输量，m3/h；n为压缩机组的转速，r/min；n0为压缩机组的额定转速，r/min。

2 性能误差修正

2.1 误差分析

随着使用年限的增加，离心压缩机组性能相比出厂时有所劣化[15]。对某压气站3台型号相同的离心压缩机组进行分析，性能参数(功率、压比)实测值与经过相似换算后的理论值进行对比，得到两者的相对误差曲线(图1、图2)。经统计，功率的相对误差约在20%，压比的相对误差约在9%。同时，由图1、图2可知，即使相同型号的压缩机组，其性能劣化程度也有所差异，3台离心压缩机组的性能劣化程度排序为：2#>3#>1#；并且性能劣化使性能参数(功率、压比)实测值大于理论值，随着劣化程度的增大，误差也越来越大。

因此，型号相同的压缩机组在优化运行方案时不能视作完全一致，故引入最小二乘误差修正模型。

2.2 误差修正模型的建立

误差修正思想[15]是利用实际运行数据对理论计算结果进行修正，使理论计算结果更加符合实际情况，该思想广泛应用于数值模拟[16]和图像识别[17]领域。

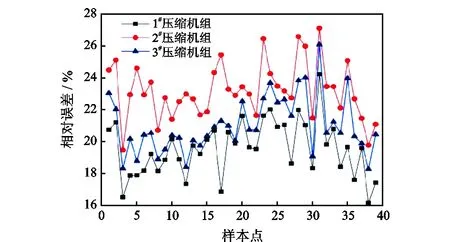
图1 各压缩机组功率实测值与理论值的相对误差Fig.1 Relative errors between measured values and theoretical values of power of compressor units

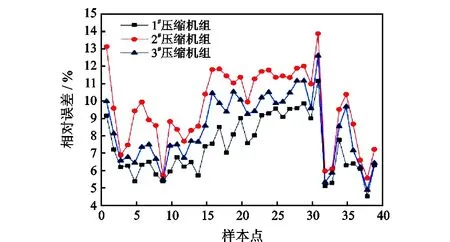
图2 各压缩机组压比实测值与理论值的相对误差Fig.2 Relative errors between measured values and theoretical values of pressure ratio of compressor units

最小二乘误差修正模型建模步骤：取单台压缩机组设计时的功率Ntot、压比ε为自变量，取实际运行时的功率Ntot′、压比ε′为因变量，利用最小二乘法拟合原理拟合出与

(3)

ε′=mjε2+njε+tj

(4)

结构一致的误差修正公式。

式(3)、式(4)中的系数aj、bj、cj、mj、nj、tj均通过最小二乘法一元拟合原理计算得到。由该模型预测的性能参数(功率、压比)值更加接近实际。

3 压缩机组运行优化

输气管道系统的压气站内往往不止配备1台压缩机，据2.1节分析结果可知，即使同一型号的压缩机性能状态也有优劣差异，而且多台压缩机同时运行时，一台能耗最低并不代表总能耗最低。因此，在某一输气量下，当组合开机方案不唯一的时候，应该怎样选择运行方案使总能耗最低，需要建立对应的运行优化模型并求解。

压气站压缩机组运行优化是典型的混合整数非线性规划问题，一般采用遗传算法[18]和模拟退火算法[19]，但通常只能得到问题的局部最优解，且计算时间难以控制；采用BP神经网络[10]直接映射出优化运行方案，但没能预测转速；也有将问题简化为混合整数线性规划问题[20]，但将运行费用与进口流量近似为线性关系的假设应用范围十分有限。上述方法都将站内不同压缩机视作性能一致，这种假设前提下的运行方案不符合实际情况，但完全考虑各压缩机的性能差异，会令本就复杂的规划问题求解难度更大，计算时间更长。因此，本文引入了输量分配因子，降低模型求解计算量的同时尽可能保证运行方案的最优。

3.1 压缩机组运行优化模型的建立

为制定压气站内多机组联合运行方案，建立如下优化模型。

目标函数：

(5)

式中：G为所有压缩机组的总功率，kW；t为压缩机总台数；ki为压缩机状态，ki=0表示压缩机处于关机状态，ki=1表示压缩机处于启机状态。

为防止压缩机出现喘振或者堵塞工况，压缩机的转速、进出口压力和流量等均需处于允许范围内[21]，因此具体约束条件为

(6)

式中：ni为第i台压缩机组的转速，r/min；nmin、nmax为压缩机组的最小、最大转速，r/min；Q0为所有压缩机的总入口流量，m3/d；Qi为第i台压缩机组的实际输量，m3/d；Qmin、Qmax为压缩机组的最小、最大输量，m3/d；εi为第i台压缩机组的压比；εmin、εmax为压缩机组的最小、最大压比，无因次；Ni为第i台压缩机组的功率，kW；Nmin、Nmax为压缩机组的最小、最大功率，kW；Psi为压缩机组的入口压力，MPa；Psi，min、Psi，max为最小、最大进口压力，MPa；Pdi为压缩机组的出口压力，MPa；Pdi，min、Pdi，max为最小、最大出口压力，MPa。

模型假设：多机组联合运行时每台压缩机组的出口压力和进口压力相等，即压比相等。

3.2 模型求解步骤

当某压气站内多机组联合运行时，因为各压缩机组性能不同，采用均分流量的运行方式，制定的多机组联合运行方案可能会使某些压缩机发生喘振或者堵塞，所以在解模过程中引入输量分配因子

(7)

单台压缩机组的实际输量为

Qi=Q×Si。

(8)

式中：Si为第i台压缩机组的输量分配因子，当只有1台压缩机组运行时Si=1；Ns为未劣化压缩机组在某一确定输量、确定转速情况下的功率，kW；Nsi为已劣化压缩机组在某一确定输量、确定转速情况下的功率，kW；Q为当只有1台压缩机组运行时，即为总输量，当有多台压缩机组联合运行时，即单台的均分输量，m3/h；Qi为当有多台压缩机组联合运行时，第i台压缩机组的实际输量，m3/h；m为开启的压缩机组台数。

在解模过程中，输量分配因子Si越大，代表压缩机组性能越好，因此可以通过对比不同压缩机组Si的大小，优先选择性能更好的压缩机组。在给定某一压气站输量任务时，解模步骤如下：

步骤1：给定初值。转速n为压缩机组的最小转速nmax，压气站内所有压缩机组总功率为一个不可能达到的极大值Nmax，压缩机组开启台数i为1台，针对某一输量任务所确定的压气站最低出站压力Pd为Pmin；

步骤2：压气站内的压缩机组开启台数m从1到t依次枚举，t为站内压缩机组总数，先假定每台压缩机组性能完全相同，每次枚举都采用均分的流量分配方式；

步骤3：当开机数为m时，利用式(1)—(2)，在压缩机组转速允许范围内依次枚举转速n，求得满足出口压力要求的最小功率N(前面Nmin已经表示了压缩机组的最小允许功率，此处确定采用N，不作更改)，以及最小功率对应的转速n、输量Q和所有压缩机组的总功率Ntot(前面设计工况下的功率改用Ns表示)；

步骤4：压缩机组开启台数m从1到t依次枚举的过程中，求得使总功率Ntot最小的开机方案，得到该方案下的开启台数m、单机输量Q、转速n；

步骤5：在步骤4得到的开机方案下，利用式(3)—(4)，分别计算每台压缩机组的压比εi、功率Ni，根据式(7)—(8)分别计算每台压缩机组的流量分配因子Si、单机输量Qsi；

步骤6：每台压缩机组再依次枚举转速n，根据式(3)—(4)，分别计算每台压缩机组在满足出口压力、输量要求情况下的最小功率Nif，所有压缩机组最小功率的总和就是该压气站的总功率G。

具体解模过程如图3所示。 在输量任务确定的情况下，通过上述解模流程，可以计算得到使压气站总功率最小的多机联合运行方案。

图3 模型求解框图Fig.3 Model solving block diagram

4 现场应用

4.1 站场简介

榆济输气管道某压气站采用4台新比隆公司同一型号的大功率离心压缩机组，目前按最高输气量下3运1备的运行方案工作。其中1#、2#、3#压缩机组于2010年12月投产运行至今，性能有不同程度劣化。在设计工况(3.901 3 MPa，45 ℃)下，该型号压缩机组在不同转速下的性能曲线如图4所示。基于最小二乘法曲面拟合原理，对图4所示的性能曲线进行拟合，相对误差在1%以内。

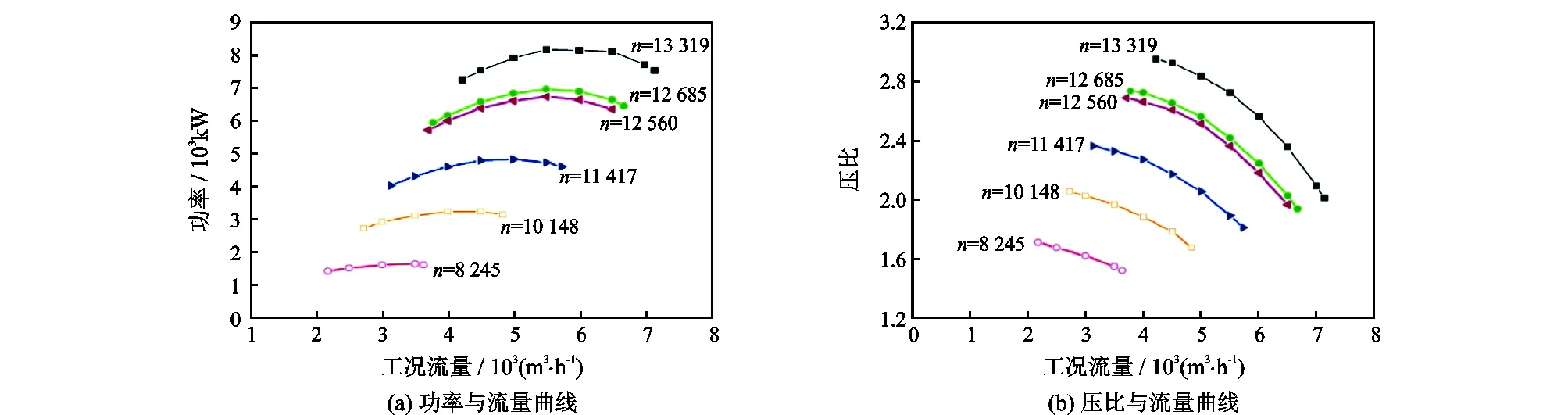
图4 压缩机组的性能曲线Fig.4 Performance curves of compressor units

4.2 应用结果分析

取该压气站2017年的部分历史运行数据，利用误差修正模型，得到1#、2#、3#压缩机组的性能参数(功率、压比)预测值与实测值的相对误差曲线(图5、图6)。

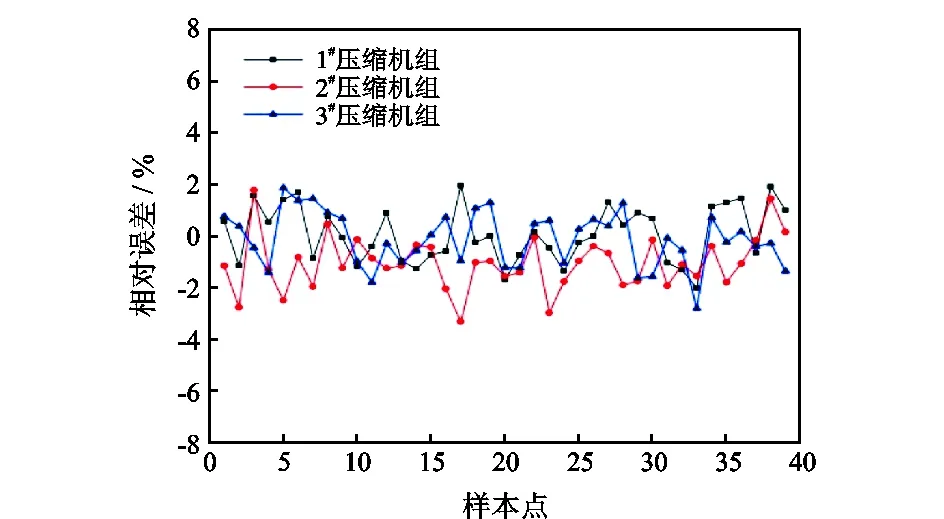
图5 各压缩机组功率预测值与实测值的相对误差Fig.5 Relative errors between predicted values and measured values of power of compressor units

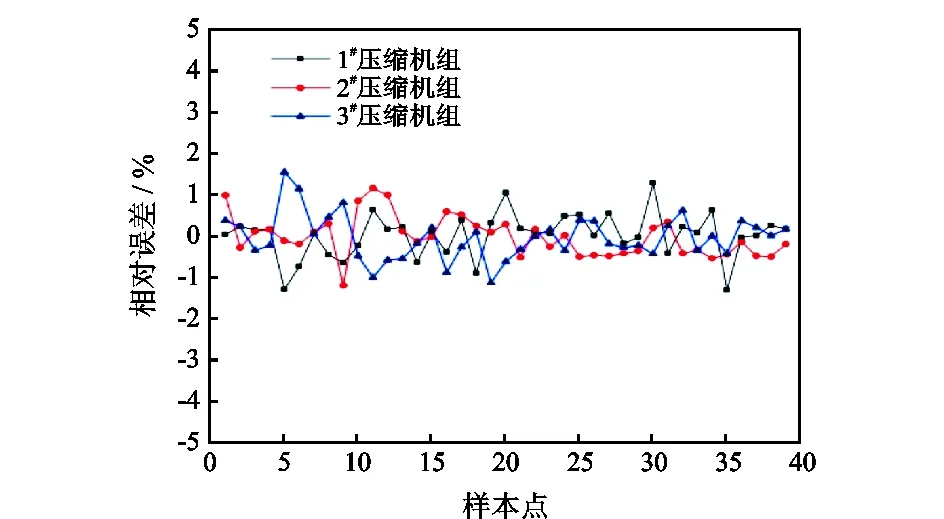
图6 各压缩机组压比预测值与实测值的相对误差Fig.6 Relative errors between predicted values and measured values of pressure ratio of compressor units

从图5、图6可以看出，由误差修正模型预测的性能参数(功率、压比)值与实测值的相对误差在3%以内，平均相对误差为1.2%，可见该模型能为多机组联合运行方案的制定提供比较符合实际的数据基础。

该压气站配备了4台压缩机，其中4#机组因为投产时间最短，性能最好，故不再分析相对误差，其次是1#和3#机组，因此选取4#、1#和3#机组制定运行方案，开机优先顺序依次为4#、1#、3#。当某台机组单机流量、转速和单机功率中任一个值为0时表示该机组处于关闭状态。挑选该压气站2017年不同工况下的部分历史运行数据对运行优化模型的可靠性进行验证，将由运行优化模型制定的多机联合运行方案的总能耗与历史运行方案的总能耗进行对比，结果见表1，表中所示工况至少都需要2台机组同时运行，工况6、7甚至需要3台机组同时运行。

与压缩机组历史运行方案的耗电量相比，由运行优化模型制定的多机组联合运行方案降低了压缩机组的总能耗，平均能耗降幅约为4%，验证了基于误差修正模型的压缩机组运行优化模型的可靠性。可见，该压气站可在日输量确定的情况下，利用压缩机组运行优化模型提前制定合理的多机组联合运行方案，从而达到降低压缩机组总能耗的目的。

5 结 论

(1) 离心压缩机组性能劣化会使性能参数(功率、压比)实测值大于理论值，且随着劣化程度的增大，误差会越来越大。

表1 不同运行工况下制定的多机联合运行方案Tab.1 Multi-machine joint operation schemes under different operation conditions

(2)基于最小二乘法原理构建的误差修正模型，预测性能参数(功率、压比)的准确度在97%以上，验证了该误差修正模型的可靠性。

(3)针对不同运行工况，由压缩机组运行优化模型制定的多机联合运行方案，与历史运行方案相比能耗降幅约在4%，证明了在多机联合运行时，该模型制定的运行方案确实可以降低能耗，节省输气成本。