响应倾向得分匹配法及处理效应估计

孙玲莉，杨贵军

（天津财经大学 统计学院，天津300222；天津财经大学 中国经济统计研究中心，天津300222）

一、引言

在社会经济领域，处理效应的估计是制定相关政策及判断政策实施效果的重要基础（Tu 等，2000；胡吉祥等，2011；纪园园等，2020）[1-3]。例如，在制定吸引和留住流动人口的政策时，家庭消费水平是评价流动人口生活质量的重要方面。根据消费理论和人力资本理论，消费依赖个人收入水平，而个人收入水平主要取决于受教育程度（Keynes，1936；Schultz，1961）[4，5]。因此，合理测算流动人口受教育程度对家庭消费的影响程度具有重要的现实意义。在其他条件完全相同的假定下，受教育程度不同的家庭消费差异被视为教育对家庭消费的处理效应。

在因果推断中，处理变量取不同水平时的结果变量平均差值被称为处理效应（Treatment effect）。处理效应的估计常选用Rubin 因果模型（Rubin，1978）[6]。假设个体接受处理，则其属于处理组，标记T=1；个体未接受处理作为对照，属于控制组，标记T=0。两组个体的潜在结果分别记为Y1、Y0，处理效应τ=E（Y1-Y0）。在完全随机化的可控实验中，处理组与控制组的个体具有同质性，处理效应τ=E（Y1-Y0）=E（Y1∣T=1）-E（Y0∣T=0）。在非随机化实验中，每个个体只能观测到一个潜在结果，未观测到的结果被称为反事实（Counterfactuals）（Paul and Rubin，1983；Rubin and Thomas，1996）[7，8]。现实中一些不可控的影响因素往往会使处理组与控制组产生个体选择偏误（Lalonde，1986）[9]，导致处理效应估计的可信度降低。此时，处理效应τ=E（Y1-Y0）≠E（Y∣T=1）-E（Y∣T=0）。经济问题研究中常出现这类问题，其原因是存在客观成本和人伦道德的约束，完全的随机化实验难以实施（韩锋和隋福民，2015）[10]。为了消除个体选择偏误，学者们主要采用了两类方法。（1）倾向得分匹配法（Propensity score matching）。倾向得分是指给定协变量的情形下个体属于处理组的条件概率（Paul and Rubin，1983）[7]。分别来源于处理组和控制组的两个个体的倾向得分若相近或相等，则两者匹配，对应的处理组为反事实匹配组。利用处理组和反事实匹配组估计处理效应，能够有效消除个体选择偏误对处理效应的影响。倾向得分匹配法易于使用，其对高维协变量匹配的效率高，故该方法现已得到广泛应用（卢闯等，2015；胡宏伟等，2012）[11，12]。（2）断点回归方法和双重差分法。断点回归方法是按是否接受处理将观测数据划分出临界点，观测数据即处于断点的两侧，根据断点两侧的样本数据就可以估计处理效应（Thistlethwaite and Campbell，1960）[13]。双重差分法主要是估计分组变量与时间变量的交叉项（Abadie，2005）[14]。

在现有研究中，有关处理效应的估计主要存在两个缺陷。首先，断点回归的估计结果依赖预先设定的模型，结果变量是否受到其他处理因素的影响是很难识别的（余静文和王春超，2011）[15]。双重差分法的假设条件较为严格，平行趋势假定（Parallel trend）难以得到满足（陈林和伍海军，2015）[16]。其次，倾向得分匹配法是根据接受处理分组的示性变量建立模型，拟合模型容易受到处理组和控制组样本差异的影响，从而导致模型无法收敛。此外，如果不能较好地平衡处理组和控制组协变量与响应变量的相关性，处理效应估计的系统偏差就会增大。

基于此，本文在倾向得分匹配法的基础上引入一种新的方法——响应倾向得分匹配法（Response Propensity Score Matching）（杨贵军等，2018）[17]。相应地，本文将原来的倾向得分匹配法称为类别倾向得分匹配法（Categorical Propensity Score Matching），以示区别。响应倾向得分匹配法最早是用于处理调查数据中的无回答问题，本文借鉴该思路，将处理效应中的控制组和处理组分别视为回答组和无回答组，用于处理效应的估计。

响应倾向得分匹配法的基本思想是将控制组的结果变量观测值按大小进行排列并取秩，对结果变量的秩计算累计概率，再与协变量建立响应倾向得分模型，寻找控制组的反事实匹配组，利用反事实匹配组估计处理效应。响应倾向得分匹配法不严格要求处理组和控制组的样本容量，这就弥补了类别倾向得分匹配法的不足。此外，利用结果变量观测值的秩变换与协变量建立模型，可以保持协变量与响应变量之间的相关性一致，减少个体选择偏误，提高处理效应估计的可信性。相比于断点回归和双重差分法，响应倾向得分匹配法的限制更少，更便于操作。

二、响应倾向得分匹配法

若记T为个体接受处理的示性变量，则T=1 代表个体接受处理，T=0 代表个体未接受处理。X=（X1，X2，…Xk）′为k维协变量，Y表示个体的结果变量。其中，（X0，i，Y0，i）（i=1，…，nc）为控制组，（X1，j，Y1，j）（j=1，…，nt）为处理组，样本量分别为nc、nt，样本均值分别为每个个体只有一个观测结果，或者属于处理组，或者属于控制组。若个体不存在选择偏误，则处理效应如下：

在多数情况下，个体是存在选择偏误的，则处理效应为：

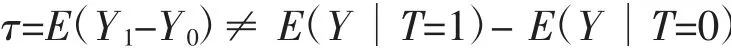
显然，直接使用样本均值之差估计处理效应τ，则会出现系统偏差。

在非随机实验中，保证处理组和控制组个体协变量尽可能相同是估计处理效应τ 的前提。Paul和Rubin（1983）[7]提出了倾向得分匹配法（本文称其为类别倾向得分匹配法），将类别倾向得分定义为给定协变量X条件下个体接受处理的条件概率，即有：

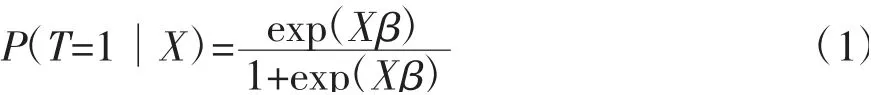
如果类别倾向得分相同或近似相等，两个个体就是匹配的，相应的控制组个体被称为处理组的反事实匹配个体。处理组与反事实匹配组个体之间的协变量相似，可以直接估计处理效应。类别倾向得分匹配法需要满足两个基本假定（Caliendo and Kopeinig，2008）[18]。

假定1：给定协变量X，个体接受处理与否都和结果Y相互独立。

假定2：给定协变量X，个体接受处理与否的概率均为正。

在类别倾向得分匹配法的实际应用中，处理组与控制组样本容量差异过大会导致Logistic 模型参数估计无法收敛，而且类别倾向得分匹配法不能保证处理组与控制组中协变量与响应变量的相关性一致。因此，响应倾向得分匹配法改进的基本思路是，将控制组结果变量观测值按从小到大的顺序排列取秩，对秩计算累计概率，再与协变量建立响应倾向得分模型，利用拟合的响应倾向得分模型分别计算处理组与控制组个体的响应倾向得分，并将与处理组个体响应倾向得分差异小的控制组个体作为处理组的反事实匹配组个体。这样做就能在很大程度上保持匹配个体的协变量与结果变量之间的一致相关性。

响应倾向得分匹配法的创新之处在于引入了秩统计量，而秩统计量不受分布影响，应用更加广泛（Spearman，1904；Torra 等，2006）[19，20]。统计模型的建立若考虑分类变量的有序性，则可以弥补连续变量假定的缺陷。引入秩变换保证了结果变量观测值的大小不发生错序，对秩计算累计概率使得结果变量观测值保持在0 至1 区间，倾向得分模型的拟合效果以及控制组与处理组的匹配效果都得到了改进。相比于倾向得分匹配法，响应倾向得分匹配法是基于控制组数据建立模型，避免了控制组与处理组样本量差异对模型的影响。具体而言，响应倾向得分匹配法的使用主要包括四个步骤。

（一）计算响应变量秩的累计概率

将控制组（T=0）的结果变量Y的观测值y0，i（i=1，2，…nc）按从小到大的顺序排列，我们得到：y0，1′＜y0，2′＜…，y0，n′c。记观测值y0，i（i=1，2，…nc）的秩为R0，i（y0，i），则响应变量Y取R0，i（y0，i）的概率为：

累计概率为：

根据样本观测值，选择观测值秩序的累计概率估计如下：

（二）建立响应倾向得分模型

本文以样本结果变量观测值秩序的累计概率值为被解释变量，以协变量X0，i（i=1，2，…nc）为解释变量，建立响应倾向得分logit 模型：

将式（3）代入式（4），则有：

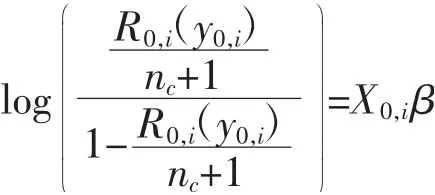
响应倾向得分为：

其中，0≤P（Y≤R0，i（y0，i）∣X0，i）≤1。将全部个体的协变量代入拟合模型，我们分别得到控制组和处理组个体的响应倾向得分。

（三）匹配反事实个体

本文定义响应倾向得分的距离为绝对值距离，即处理组个体j与控制组个体i若匹配，则计算它们的响应倾向得分距离：

假定处理组个体j与控制组nc个个体的响应倾向得分距离满足：

处理组个体j与控制组中的第一个个体的响应倾向得分距离最小，控制组中的第一个个体就作为处理组个体j的匹配个体。将处理组个体y1，j（j=1，2，…nt）依次与控制组个体y′0，j（j=1，2，…nt）相匹配，则与处理组相匹配的控制组为反事实匹配组。

（四）估计处理效应

本文利用处理组和反事实匹配组个体估计处理效应，处理效应为：

相应的估计量为：

响应倾向得分匹配法保留了类别倾向得分匹配法的优势，具有较高的个体匹配计算效率。此外，响应倾向得分匹配法具有较好的Logistic 模型拟合效果，其不需对处理组和控制组的样本量差异大小进行严格规定，处理效应估计的可靠性更高。

三、响应倾向得分匹配法下处理效应估计量的统计性质模拟研究

本文利用模拟的方法研究响应倾向得分匹配法及处理效应估计量的统计性质，并与类别倾向得分匹配法进行比较，模拟方法参考杨贵军等（2016）[21]的研究。在实际的经济问题研究中，多元线性回归模型的应用是最为广泛的，故本文也选择如下线性回归模型：

其中，X1、X2为连续变量，X3、X4、X5、X6为离散变量，T为处理变量。考虑到后文的实证数据，这里设定处理效应τ=0.5，同时选取ε 为服从正态分布N（0，0.15）的随机误差项。对于处理组T=1，本文分别从正态分布N（1 500，250）、N（4 800，600）及两点分布B（1，0.4）、B（1，0.6）、B（1，0.8）、B（1，0.05）中独立随机抽取nt=600 个随机数作为协变量X1、X2、X3、X4、X5、X6的观测值，系数分别为β0=0.6，β1=0.6，β2=0.2，β3=0.03，β4=0.12，β5=-0.03，β6=-0.05。对于控制组T=0，本文分别从正态分布N（1 200，200）、N（4 000，630）及 两 点 分 布B（1，0.2）、B（1，0.6）、B（1，0.2）、B（1，0.85）中独立随机抽取nc=4 500 个随机数作为变量X1、X2、X3、X4、X5、X6的观测值，系数分别设定为β0=0.6，β1=0.6，β2=0.2，β3=0.03，β4=0.05，β5=0.03，β6=0.05，并对连续协变量取对数。利用线性回归模型，本文计算出处理组600 个个体的结果变量观测值和控制组4 500 个个体的结果变量观测值。

本文分别采用类别倾向得分匹配法和响应倾向得分匹配法估计处理效应τ。为了保证估计结果的稳定性，上述模拟过程重复了200 次。对于类别倾向得分匹配法和响应倾向得分匹配法，每次重复模拟的处理效应估计值记为和并取处理效应200 估计值平均代表处理效应估计的期望。本文选择处理效应估计的偏差和均方误差作为方法应用优劣的评价指标。偏差是指处理效应估计值的期望与真值τ=0.5 之差，即，处理效应估计值与真值τ=0.5 差值平方的平均数为均方误差，偏差和均方误差越小越好。

为了比较样本量对两种倾向得分匹配法的影响，本文采用不重复匹配法，选取与处理组个体响应倾向得分距离最小的控制组中K个不同个体进行匹配，得到K个反事实匹配组。第一个反事实匹配组与处理组个体响应倾向得分距离最小，第K个反事实匹配组与处理组个体响应倾向得分距离最大，即处理组每个个体与其反事实匹配组个体的响应倾向得分距离满足dj，1≤dj，2≤dj，3…≤dj，k-1≤dj，k。这里，本文选择K=7。

表1 给出了利用处理组与第k（k=1，2，…7）个反事实匹配组数据及处理效应的估计结果，其中，第三列是处理效应估计的期望，第四列是处理效应估计的偏差，第五列是处理效应估计的均方误差。总体来看，类别倾向得分匹配法和响应倾向得分匹配法的处理效应估计偏差和均方误差均较小，两种方法对处理效应的估计都较好。处理效应估计的统计性质与处理组和反事实匹配组之间倾向得分的距离有关，随着反事实匹配组号k的增加，类别倾向得分匹配法和响应倾向得分匹配法的处理效应估计偏差和均方误差都呈现递增趋势。因此，随着处理组与反事实匹配组之间倾向得分差异的增大，处理效应估计的偏差和均方误差也在增大。表1 的结果显示，当k≤3 时，响应倾向得分匹配法的处理效应估计偏差和均方误差都小于类别倾向得分匹配法的处理效应估计偏差和均方误差。当k≥4 时，响应倾向得分匹配法的处理效应估计偏差和均方误差都大于类别倾向得分匹配法的处理效应估计偏差和均方误差。当k=1 时，两种倾向得分匹配法的处理效应估计偏差和均方误差都为最小。相对来说，响应倾向得分匹配法的处理效应估计要优于类别倾向得分匹配法，其更接近于处理效应的真值。因此，响应倾向得分匹配法的处理效应估计更优，利用与处理组响应倾向得分距离最小的k=1 反事实匹配组估计处理效应是最好的。

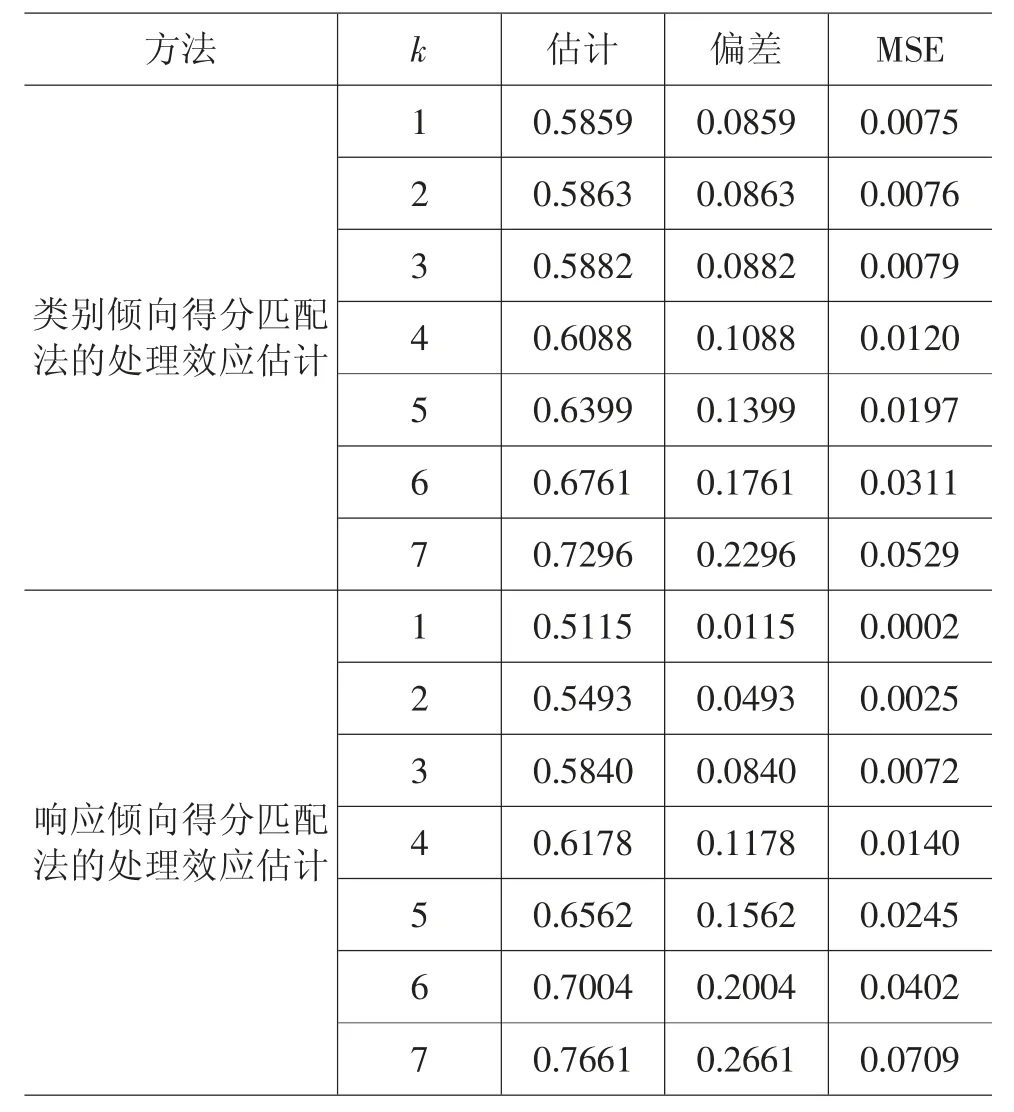
表1 处理效应估计的偏差和均方误差

四、流动人口受教育程度对家庭消费差异影响的实证分析

各地区要想加快经济发展，必须制定吸引和留住流动人口的政策，保证流动人口的生活质量，而家庭消费是评价流动人口生活质量的重要方面。近年来，消费发展趋势问题受到学者们的高度关注（殷俊茹等，2016）[22]。影响消费的因素有很多，教育是其中的一个重要因素（Song，2008；杨碧云等，2014）[23，24]。在其他条件完全相同的假定下，受教育程度不同的家庭消费差异可以视作教育对家庭消费的处理效应，合理测算流动人口家庭消费的教育效应具有重要的现实意义。

国内外的研究者多是基于调查数据测算受教育程度对消费的影响，认为教育对消费具有正向作用。由于调查数据往往存在自选择偏误，这种自选择偏误容易使分析结论产生偏差。自选择偏误是指非完全随机化样本所导致的分析结论偏差，其产生的根源是调查数据中的居民受教育程度并不是完全随机的。在完全随机的调查数据中，除教育程度是不同质的，居民家庭状况、工作环境和收入等变量则具有同质性，即家庭状况、工作环境和收入等变量对家庭消费的整体影响作用相同，这些变量可以称为协变量。受客观成本和人伦道德的约束，完全的随机化调查是难以实施的（韩锋和隋福民，2015）[10]。在非完全随机的调查数据中，受教育程度不同居民的协变量不具有同质性（Lalonde，1986）[9]，生活习惯、工作状况和收入都不一致。因此，流动人口受教育程度对家庭消费的影响应该包括两个部分：一部分是在居民生活、工作状况和收入等协变量相同条件下两类家庭的平均消费支出差值，是居民家庭状况、工作环境和收入等协变量同质时，仅由受教育程度不同所导致的家庭消费差异；另一部分是教育通过改变生活习惯、工作状况和收入等协变量，间接影响家庭消费支出。因此，研究协变量相同条件下两类居民家庭的平均消费支出差值，对于揭示流动人口受教育程度影响家庭消费的机制具有重要意义。现有文献没有区分受教育程度对家庭消费所产生的不同影响，本文则利用响应倾向得分匹配法分析流动人口受教育程度对家庭消费所产生的处理效应，以期减少居民个体选择偏误，得到更合理的估计结果。

（一）变量选择

有关教育对消费影响的研究多是基于家庭生产理论（Becker，1964；Becker，1978）[25，26]，认为教育水平高的个人消费水平较高，对新产品的购买意愿也较强（Michael，1972）[27]。Hettich（1972）[28]研究发现，教育水平高的女性购买行为效率更高。Wang（1995）[29]基于美国消费者支出数据的研究显示，户主受教育程度高的家庭在饮食消费上的支出也更多。Wagner等（1988）[30]、Tansel 等（2006）[31]分别使用美国和土耳其的调查数据进行了分析，发现夫妻二人的受教育程度对消费具有正向影响。国内的研究显示，居民受教育程度对消费影响的结论与国外的研究基本一致，即教育对消费具有正向作用。刘曦子等（2018）[32]认为，居民受教育程度对消费具有显著影响，动态面板分位数回归给出的受教育程度系数为0.3～0.5，即某地区大专以上学历（含大专）的人口占比每提高1 百分点，该地区的消费就增加0.3%～0.5%。刘子兰等（2018）[33]将受教育程度作为人力资本的代理变量，使用混合OLS 模型测算了教育对居民消费的影响，发现户主受教育年限每增加1 年，家庭消费性支出、生存性消费、享受性消费分别增长1.71%、1.42%、2.47%。王弟海等（2017）[34]的面板回归模型分析结果显示，生产部门中人均受教育年限每增加1 年，人均GDP 增长率平均提高0.7～1.4 百分点。杨碧云等（2014）[24]研究发现，户主受教育程度与服务性消费负相关，与其他支出正相关。

目前，有关流动人口家庭消费影响因素的研究大多集中于户籍制度、医疗社会保障、居住意愿、个人收入等方面（谭苏华等，2015；周明海和金樟峰，2017；张义等，2020；孙文浩，2020；赵锦春等，2019）[35－39]。基于此，本文选择流动人口的家庭平均月总支出水平测度家庭消费，即将上年家庭在本地的平均月总支出作为结果变量，将流动人口受教育程度作为处理变量。本文将居民受教育程度分为两类，即大学专科以下、大学专科及以上。大学专科以下包括未上过学、小学、初中、高中/中专，大学专科及以上包括大学专科、大学本科和研究生。每个居民的教育程度是已知的，其只能属于上述分类中的某一类，而不能同时属于两个类别。借鉴谭苏华等（2015）[35]的研究，本文的协变量主要考虑经济、家庭和社会三个方面。经济变量包括上年家庭在本地的平均月总食品支出和个人上月收入，家庭变量包括性别和婚姻状况，社会变量包括就业单位的性质（是否为集体企业、个体工商户或港澳台独资企业）和户主的就业身份（是否为雇主或自营劳动者），婚姻状况包括已婚和单身（已婚包括初婚和再婚，单身包括未婚、离婚和丧偶）。对于其他影响家庭消费的变量，鉴于数据的可得性及研究目的，本文暂不考虑。

本文选取2015 年全国流动人口卫生计生动态监测调查户籍人口问卷（A 卷）中天津市的调查数据进行研究，其基本信息见表2。流动人口卫生计生动态监测调查中的天津市样本容量为5 116 个，其中，大学专科及以上类别中有574 个，大学专科以下类别中有4 542 个。

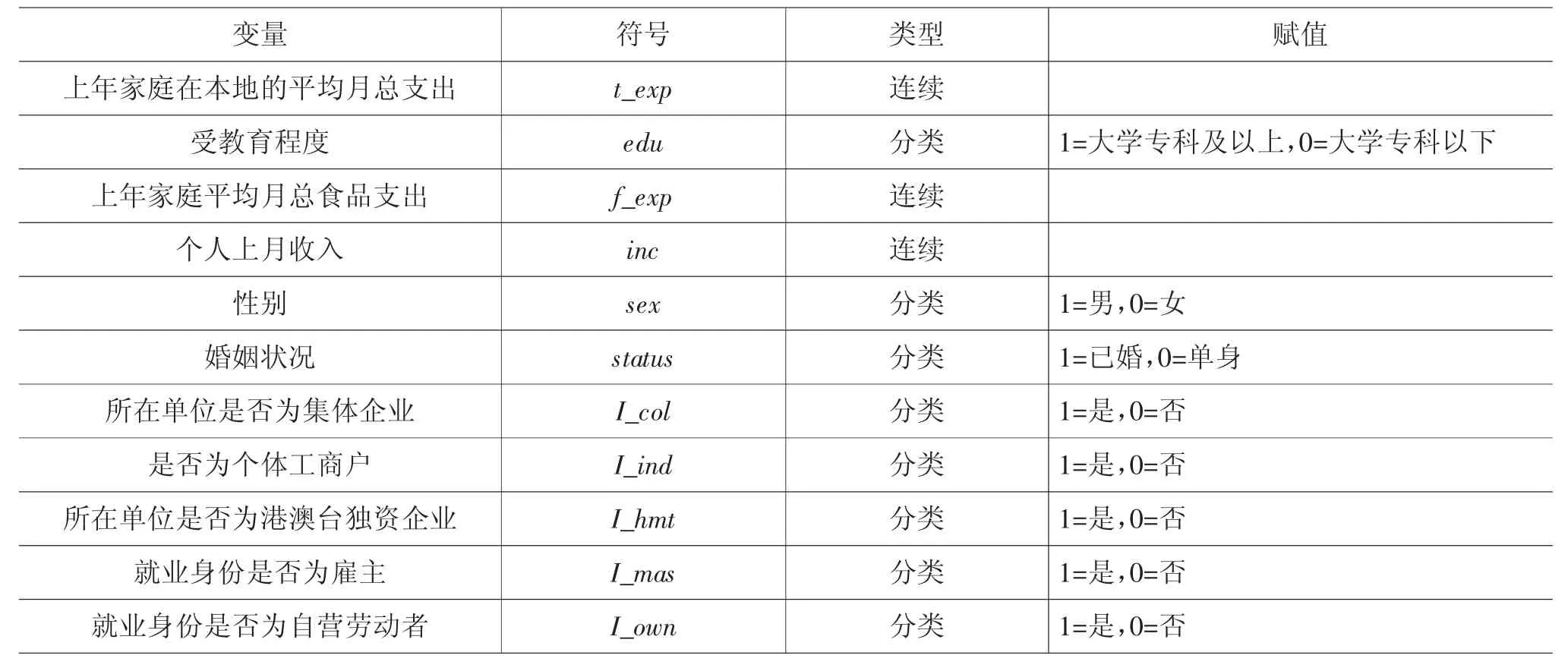
表2 变量描述

表3 报告了全部样本均值、574 个教育程度高的样本均值、4 542 个教育程度低的样本均值以及教育程度不同居民样本均值的差值。可以看出，教育程度高（edu=1）的家庭消费（t_exp）均值高于教育程度低（edu=0）的家庭消费均值，教育程度高的居民收入（inc）均值也普遍高于教育程度低的居民收入均值。从离散变量来看，除单位是否为港澳台独资（I.hmt）外，其他变量中教育程度高的居民大部分均值低于教育程度低的居民均值。在两个类别的协变量中，除了性别比例差异不大外，其他协变量的均值差异都较大，容易形成自选择偏误，可能影响教育对家庭消费支出的处理效应。直接用两类家庭消费支出的差值1 016.287 9 元作为家庭消费的匹配教育效应估计可能会产生系统偏差，因为这个差值是两类家庭消费的教育效应，不仅包括家庭消费的匹配教育效应，还包括其他协变量不同质的非匹配教育效应。因此，只有利用教育程度不同居民的协变量进行匹配，减少样本自选择偏误的影响，家庭消费差值才能更好地反映家庭消费的匹配教育效应。

表3 不同教育类别的变量均值比较

（二）基于响应倾向得分的反事实匹配组

本文采用响应倾向得分匹配法估计流动人口受教育程度对家庭消费的处理效应。edu=1 的个体为处理组，edu=0 的个体为控制组，为edu=1 处理组个体匹配edu=0 控制组个体，即可得到反事实匹配组，用于计算教育对家庭消费的处理效应。

首先，本文计算响应变量秩的累计概率。将edu=0 控制组中4 542 个观测t_exp0按从小到大的顺序排列，得到t_exp0，1，…，t_exp0，4542，取秩分别为R0，i（y0，i）（i=1，…，4542），则每个控制组响应变量秩序的累计概率为：

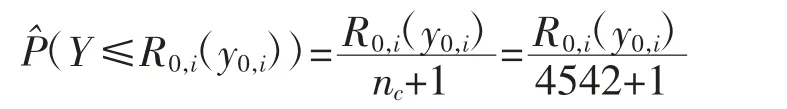
其次，本文采用响应倾向得分模型，基于edu=0控制组的4 542 个观测数据建立Logistic 模型。其中为被解释变量，解释变量分别为平均月总食品支出f_exp、个人上月收入inc、性别sex、婚姻状况status、所在单位是否为集体企业I_col、是否为个体工商户I_ind、所在单位是否为港澳台独资企业I_hmt，就业身份是否为雇主I_mas、是否为自营劳动者I_own。本文使用Logistic 回归拟合模型，依据模型计算控制组中4 542 个个体的响应倾向得分，将edu=1 处理组中574 个个体的协变量代入拟合模型，即可得到处理组个体的响应倾向得分。从edu=0 控制组的4 542 个个体中分别找出与edu=1 处理组574 个个体响应倾向得分距离尽可能接近0 的匹配个体，其即构成反事实匹配组。

为了进一步分析响应倾向得分匹配法的有效性，本文进行了匹配后样本的平衡性检验，主要比较处理组与反事实匹配组的样本均值差和样本方差比率。处理组与反事实匹配组之间样本均值的差值越小，方差比率越接近于1，处理组与反事实匹配组的样本差异就越小。

从表4 基于响应倾向得分匹配法的处理组与反事实匹配组平衡性检验结果来看，连续变量匹配后的均值差明显降低。平均月食品支出f_exp未匹配时的均值差为300.860 1 元，匹配后的均值差仅为31.829 3 元，方差比率为1.063 8。个人月收入inc未匹配前的均值差为775.263 2 元，匹配后的均值差为297.020 9 元，方差比率为1.004 1。离散变量除了单位是否为港澳台独资I.hmt和就业身份是否为雇主I.mas外，其他离散变量匹配后的均值差值都显著小于匹配前的均值差值，特别是所在单位是否为集体企业I.col匹配前的均值差为-0.054 3，匹配后的均值差为-0.008 7，而就业身份是否为自营劳动者I.own匹配前的均值差为-0.218 7，匹配后的均值差为-0.101 0。从方差比率来看，匹配后几乎所有变量的方差比率都更接近于1。总之，响应倾向得分匹配法可以有效降低教育程度不同的两类居民的样本自选择偏误，两类居民的协变量差异更小，分布也更加接近。

表4 响应倾向得分匹配法的协变量平衡性检验结果

（三）处理效应估计

利用处理组和反事实匹配组，本文估计了流动人口受教育程度对家庭消费的处理效应。本文将处理组的每个家庭消费支出t_exp1与其反事实匹配样本家庭消费支出t_exppipei做差并取均值，即可得到在控制其他协变量匹配条件下教育对家庭消费t_exp的处理效应。

若将处理组的574 个观测全部考虑在内，不考虑重复抽取多次，且设定K=1，则响应倾向得分匹配法的处理效应为：

家庭消费的匹配教育效应占家庭消费教育效应（1 016.287 9）的48.02%，非匹配教育效应占家庭消费教育效应的51.98%，二者的占比约为1∶1。

类别倾向得分匹配法估计的处理效应为：

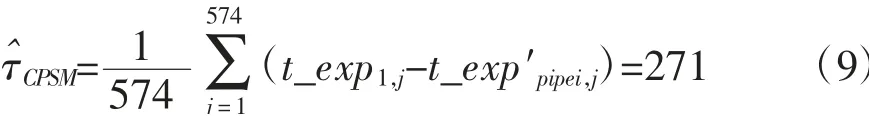
本文采用类别倾向得分匹配法计算得到天津市流动人口家庭消费的匹配教育效应占家庭消费教育效应（1 016.287 9）的26.67%，非匹配教育效应占家庭消费教育效应的73.33%，二者的占比约为1∶3。在计算处理效应的过程中，本文剔除了异常值。

为了检验处理效应估计的可信度，本文采用Bootstrap 抽样方法，重复抽取处理组574 中的450个观测值，共重复抽取200 次，分别得到200 个处理效应的估计值，并取200 个估计值的均值代表处理效应的期望。本文选择控制组中与处理组响应倾向得分距离最小K个单元作为K个反事实匹配单元，得到K个反事实匹配组，这里设定K=3。由于不知道处理效应的真值，无法评价偏差与均方误差，本文仅给出估计结果和标准差。从表5 重复抽取处理组的估计结果来看，整体而言，标准差和变异系数要比类别倾向得分匹配法的估计结果更小，说明响应倾向得分匹配法的估计值更为稳定。随着K的增加，响应倾向得分匹配法的估计值和标准差递增幅度都在减小。

表5 重复抽取处理组450 个观测得到的结果

从图1 给出的使用类别倾向得分匹配法和响应倾向得分匹配法得出的处理效应估计值箱线图来看，类别倾向得分匹配法处理效应估计值的最小值、下四分位数、中位数、上四分位数、最大数分别为98、194、222、259、355，响应倾向得分匹配法相应的值分别为271、321、341、363、416。可见，式（8）的处理效应估计结果均在合理的范围之内，而且响应倾向得分匹配法的处理效应估计值要比类别倾向得分匹配法的处理效应估计值更大。

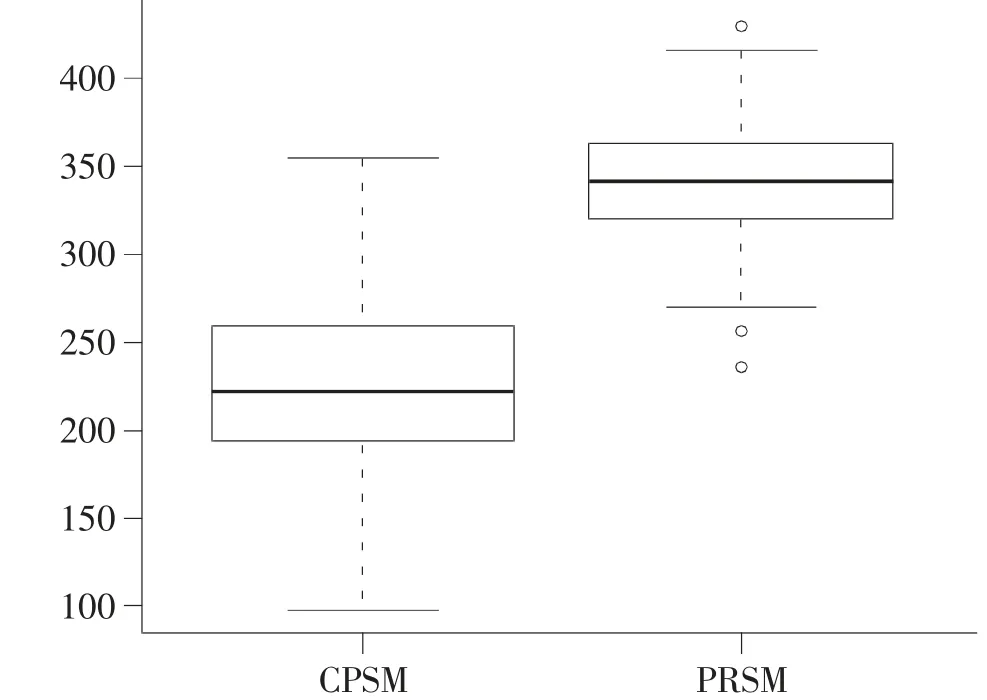
图1 两种处理效应估计值的箱线图

从以上天津市流动人口监测数据的分析结果来看，流动人口受教育程度对家庭消费确实具有显著的影响，受教育程度有助于提高家庭消费水平，这与已有文献的结论一致。在使用响应倾向得分匹配法消除样本自选择偏误之后，教育程度对家庭消费的匹配教育效应估计值占家庭消费教育效应的48.02%，该值显著大于类别倾向得分匹配法下教育效应占家庭消费教育效应的26.67%，二者的占比约为2∶1。可见，响应倾向得分匹配法消除了处理组和反事实控制组中协变量与响应变量之间相关性的差异，可以更好地估计教育对家庭消费水平的处理效应。

五、研究结论

在社会经济问题研究中，社会经济因素的不可控性使得样本收集存在自选择偏误，降低了处理效应估计的可信度。为了平衡处理组和控制组协变量的分布，缩小处理组与反事实控制组之间变量相关性的差异，本文提出响应倾向得分匹配法。响应倾向得分匹配法是将控制组的观测值按从小到大的顺序排列取秩，对秩的累计概率和协变量建立响应倾向得分匹配模型，依据拟合模型计算出样本个体的响应倾向得分，并构造反事实匹配组，利用处理组和反事实匹配组样本就可以估计处理效应。响应倾向得分匹配法既具有类别倾向得分匹配法的优点，又能有效降低处理组与反事实匹配组之间协变量相关性的影响程度。

模拟结果显示，随着处理组与反事实匹配组之间倾向得分差值的增加，类别倾向得分匹配法和响应倾向得分匹配法处理效应估计的偏差和均方误差都呈现递增趋势。相比于类别倾向得分匹配法，响应倾向得分匹配法的处理效应估计偏差和均方误差更小。如果利用响应倾向得分匹配法估计处理效应，本文建议使用最近邻匹配构造处理组和反事实匹配组。

本文考察了流动人口受教育程度对家庭消费的影响，即针对调查数据存在的自选择偏误问题，采用响应倾向得分匹配法，构造教育程度高的居民的反事实匹配组，估计家庭消费的匹配教育效应。基于2015 年全国流动人口卫生计生动态监测调查户籍人口问卷（A 卷）中天津市调查数据的实证研究显示：在消除样本自选择偏误之后，天津市流动人口受教育程度对家庭消费的匹配教育效应为488，约占家庭消费教育效应的48.02%，说明受教育程度确实提高了家庭消费水平，响应倾向得分匹配法可以更好地消除样本自选择偏误；其他协变量不同质所引致的非匹配教育效应约占家庭消费教育效应的51.98%，家庭消费的匹配教育效应与非匹配教育效应占比约为1∶1。以上结果说明，教育确实改变了人们的消费观念和消费习惯，提高了个人家庭平均月总支出水平。需要说明的是，本文所得的结论虽是基于天津市流动人口动态监测的调查数据，但其对其他省市乃至全国也具有参考价值，响应倾向得分匹配法同样适用于处理其他调查数据的自选择偏误问题。