基于数学核心素养的创新培养教学案例

刘明霞

（宁夏育才中学 宁夏银川 750011）

一、高中数学核心素养的内涵概述

数学核心素养的内涵，即学生投入到数学知识学习时，其所具有的数学思考力能否适应现代社会的发展需求，以及个人的终身发展需求，在其成长的过程中，呈现出基本的逻辑能力与思维品质。现如今，经过国内众多学者、专家的不断研究，针对数学核心素养提出了六个方面内容，即逻辑推理、直观想象、数学推算、数学建模、分析数据以及数学抽象。这六个方面是对五大基本能力的有效延伸以及更深入理解。并且，伴随新课改的持续推进，所有数学教师都将培养学生的数学核心素养，作为一项重要的教学任务。

二、数学核心素养视角下的教学策略

（一）立足源头，重视教师能力素质的提升

教师作为教学改革的设计者与执行者，其在学科核心素养的培养以及素质教育中都起到不可或缺的作用。有效培养学生的数学核心素养也需要教师具有更高的能力素质，掌握更多的教学方法才可能完成这一任务。比如说，作为数学教师，对语言的要求是简洁，逻辑性强，但有创新意识的教师会对自己的语言有更高的要求，力求数学语言也要“优美”，曾在听课中有一位教师的语言组织非常好，印象比较深的是有个同学回答完问题，她没有简单地评价好或者不好，而是这样说“你的回答带给老师一丝灵感”，这种很有创意的评价语言优美亲切，更能调动学生的积极性。教师能力素质得以提升，则能够更多地了解学生的内心世界，如此也有助于教师掌握学生当前的学习情况，使得后续教学内容的安排更具针对性，更使学生的数学核心素养得到有效培养。

（二）寓教于乐，创设情境激发学生的学习兴趣

古人云：“知之者不如好之者，好之者不如乐之者”，这句话充分阐释了兴趣对于学生的积极作用。但在教学中，仍存在部分教师不重视学生的主体地位，更习惯于课堂采用“满堂灌”的教学方式。然而，数学学科具有一定的特殊性，其对学生逻辑性要求较高，且也更显枯燥，那些复杂的推论、概念、公式及原理等，在不少学生眼中都显得晦涩难懂，自然也就无法对其产生兴趣。这就需要教师采用适当方法来激发学生的学习兴趣，进而改善此种情况，实现学生创新素养的有效培养。具体而言，教师在组织开展教学活动时，可通过创设学习情境、巧设疑点的方式，引导学生进行猜想、思索和计算的过程来调动学生学习的积极性，使学生的学习自主性得以有效提升，更进一步培养学生的创新能力。记得在一次题为“等比数列前n 项和”的“同课异构”的公开课中，四位老师在创设情境的引入上都很用心，有的引用了计算机病毒的传播的例子，有的用了网络上出现的“轻松筹”的例子，都有着较强的创新意识，和实际生活比较贴近，能够调动起学生的积极性。而上海来的一位老师仍用了教材上国王与麦粒的经典故事，但是她在这个故事的基础上进行了创新“相传古印度宰相西萨发明了国际象棋，国王想奖赏西萨。他决定在象棋的64 格上放一定数量的小麦，第一个格子一千斤，第二个两千斤，以此类推，直到第64 个格子64 千斤。而西萨听后说他想换一个方式，即第一个格子放一粒小麦，第二个格子放两粒，第三个格子放8 粒，依次类推直到第64 个格子。国王听后很困惑，觉得自己给的奖励要比西萨自己提的要求高出很多，为什么西萨会提这样的要求呢，于是国王就叫来了他的谋士帮他解惑。”这个故事教材上原本只有西萨自己的提议且只为了引入等比数列求和，但她新增加了国王也给出一个奖励方案的情节，并且后来就让学生当“国王”的“谋士”帮国王解惑，使学生既复习了前面学过的“等差数列求和”，又引入了新课“等比数列求和”。这样一个小小的创新，既没有丢失教材中原有的经典数学史料，又赋予了新的活力，让人眼前为之一亮，更大程度上引起了学生的兴趣，我在想“哦”，原来教材上的引例还可以变得这样有趣又有新意。”相信学生也为老师这样的创意感叹，这就是一个教师的创新意识带来的课堂上的改变，也为学生的创新意识埋下了种子。

（三）开发课程，进一步发展学生的创新素养

对于很多人而言校本课程都不陌生，但班本课程可能较少听到。实际上，班本课程就是根据班内学生的具体情况，以及学生对某一知识体系的掌握程度，然后对教材或是其他材料展开更进一步挖掘，进而形成适合班内学生学习的一个小课程。

去年我带的其中一个班是“云教学班”，学生的整个学习过程分课前、课中、课后，学生利用平板可以收到老师课前布置的学习任务，课上教师对集中的问题进行解答，课后还可以和教师互动交流答疑解惑。利用此优势，在上“两角差的余弦公式”时，教材中的第一种方法是几何法，即利用单位圆中的三角函数线，在做辅助线构造直角三角形时难度较大，我就做了如下尝试：

通过课前学习问题指导，学生小组合作学习，课上优秀小组分享解题思路，师生共同做点评及补充，提升。

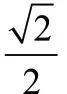
问题：你能求出cos15°的值吗？（可以借助集合工具，如三角尺等进行几何探究）试写出你的计算过程。

用几何的方法构造直角三角形求cos15°对学生来说是有难度的，所以这里特意设了一个提示，即借助用一组直角三角形拼出15°的角，由45°的直角三角形自身的直角可联想到把45°角如何做垂线放在直角三角形中，进而很自然的把60°角也能构造在直角三角形中。

2.课上学习。据学生提交的课前小组合作学习的成果，我针对有问题的解答也给他们做了批注。课上选出优秀小组分享解题思路，师生共同做点评及补充，提升。紧接着提出问题“能否将特殊角推广到任意角α，β”？此处学生应该很容易想到用α，β 分别替换60°和45°角，从而推出cos(α-β)。

但此方法是通过构造直角三角形得出的结论，所以对所有的锐角是成立的，推广到任意角还有一定的难度，可让学生课后继续探究。

引导学生从图中寻求sⅰn(α-β)，cos(α+β)及sⅰn(α+β)的几何表示，此图形还可以补全为一个矩形，四条边可以完美揭示出四组公式的线段表示，使学生体会探究的乐趣，认识到世间万物的联系与转化，这里只提供一个方向，此问题留作课后作业继续合作探究。

“由OP 的长度为1，用OM 的长表示cos(α-β)，你还能联想到什么？”

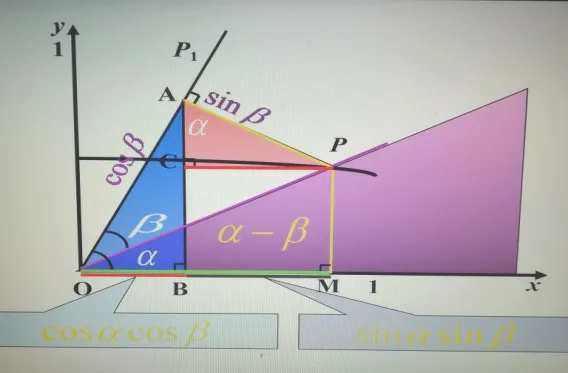
引导学生把三角函数值与它们的正弦线、余弦线联系起来.通过正、余弦线及它们之间的几何关系也可以得出cos(α-β)与cosα、cosβ、sⅰnα、sⅰnβ 之间的关系，其实此法是在第一种方法的基础上建系，构造单位圆（特殊化），从而利用三角函数线也可以得到 。此法也是教材上给出的方法，而从一般的图形再特殊化到单位圆中的三角函数线会更自然。

通过对上述问题进行思考、摸索、尝试、动手操作，可以帮助学生建构起有关“数形结合”的经验基础，因此，这一过程实际上就是学生创新素养得到培养的过程。教师在组织开展数学教学活动的时候，通过合理提问，开动学生的脑筋，调动学生思考的积极性，敢于将自身的一些独到见解发表出来，懂得客观评价，并在探索的过程中感受到数学学科所散发出的独特魅力，进而使学生在潜移默化之中养成良好的创新素养。

三、结束语

总之，伴随素质教育的不断倡导，高中数学教师所应做好的一项重要教学任务，就是不断改革教学方法，这需要教师在日常工作中善于总结，以及和其他教师展开分享、交流，从而更好培养学生的数学核心素养。