环形空心电感的设计与优化

苏达毅， 汪晶慧， 陈为

(福州大学电气工程与自动化学院， 福建 福州 350108)

0 引言

磁性元件是功率变换器的重要组成部分， 而随着开关电源进一步朝高频化和高功率密度化发展， 磁性元件的磁场泄露问题成为国内外学者关注的焦点[1-8]， 磁性元件优化设计工作的重要性愈发突出. 然而， 过去的工作往往聚焦于带磁心的电感， 对于空心电感的优化设计研究却极少.

文献[9]对比了不同频率下空心电感与带磁心电感的感值、 损耗和品质因数. 相比于带磁心的传统电感， 环形空心电感需要绕制更多的匝数来达到相应的感值， 这将带来更大的绕组损耗. 因此在低频条件下， 带磁心电感比空心电感具有更低的总损耗. 而当频率达到兆赫兹级别时， 由于空心电感没有磁心损耗而拥有更高的品质因数和更低的总损耗， 故空心电感更适用于高频应用场合. 然而， 由于空心电感环心不具备高磁导率的磁场通路， 因此存在严重的磁场泄露问题， 使其在实际应用场合中受到限制. 文献[10]讨论了带磁心环形电感泄露磁场的影响因素， 分析了磁导率变化对泄露磁场的影响， 但并未考虑磁导率为真空磁导率的情况.

空心电感的另一优势是其磁化特性具有线性性质， 其磁导率是不受激励影响的真空磁导率μ0， 故不存在磁心饱和的问题， 且其总损耗仅为绕组损耗， 损耗大小与电流激励成正比， 故也常作为标准定标电感[11-15]. 因此， 其是否具有稳定的工作特性决定了实验结果的准确性， 其泄露磁场越小， 则外界磁场对其干扰越小. 但在某些测量磁心损耗的应用场合， 需要测量空心电感的副边感应电压以排除绕组损耗对测量结果的影响， 此时漏感的存在将影响测量精度[16-17]. 研究如何减小双股并绕下空心电感的漏感可以减小此类测量实验的误差.

综上所述， 需对环形空心电感进行两方面优化： 1) 提高双股并绕环形空心电感的互感系数， 减小漏感； 2) 减小单绕组环形空心电感的泄露磁场. 本研究利用聂以曼公式和有限元仿真软件分析空心电感互感系数和泄露磁场的影响因素， 提出三种轴向泄露磁场的抑制方案， 详细讨论各方案的优缺点.

1 双股并绕空心电感的互感系数计算

双股并绕的环形空心电感结构图和二维简化模型如图1所示， 利用聂以曼公式可以分别计算其原副边自感值、 互感值， 从而进一步得到互感系数.

(1)

式中：l1表示原边绕组中心回路方程；l2表示副边绕组中心回路方程；l3表示原边绕组外侧回路方程；R1表示dl1与dl2的距离；R2表示dl1与dl3的距离；d1表示原边绕组总匝长.

由于环形空心电感为轴对称结构， 故只需先构造单匝绕组模型， 再经旋转变换后即可得到完整的原边或副边绕组模型. 以截面为矩形的空心电感原边绕组中心回路方程l1的构建为例， 首先， 确定单匝绕组四条线段的顶点坐标分别为kj=(xj，yj，zj)，j=0， 1， …， 4， 如图2所示.

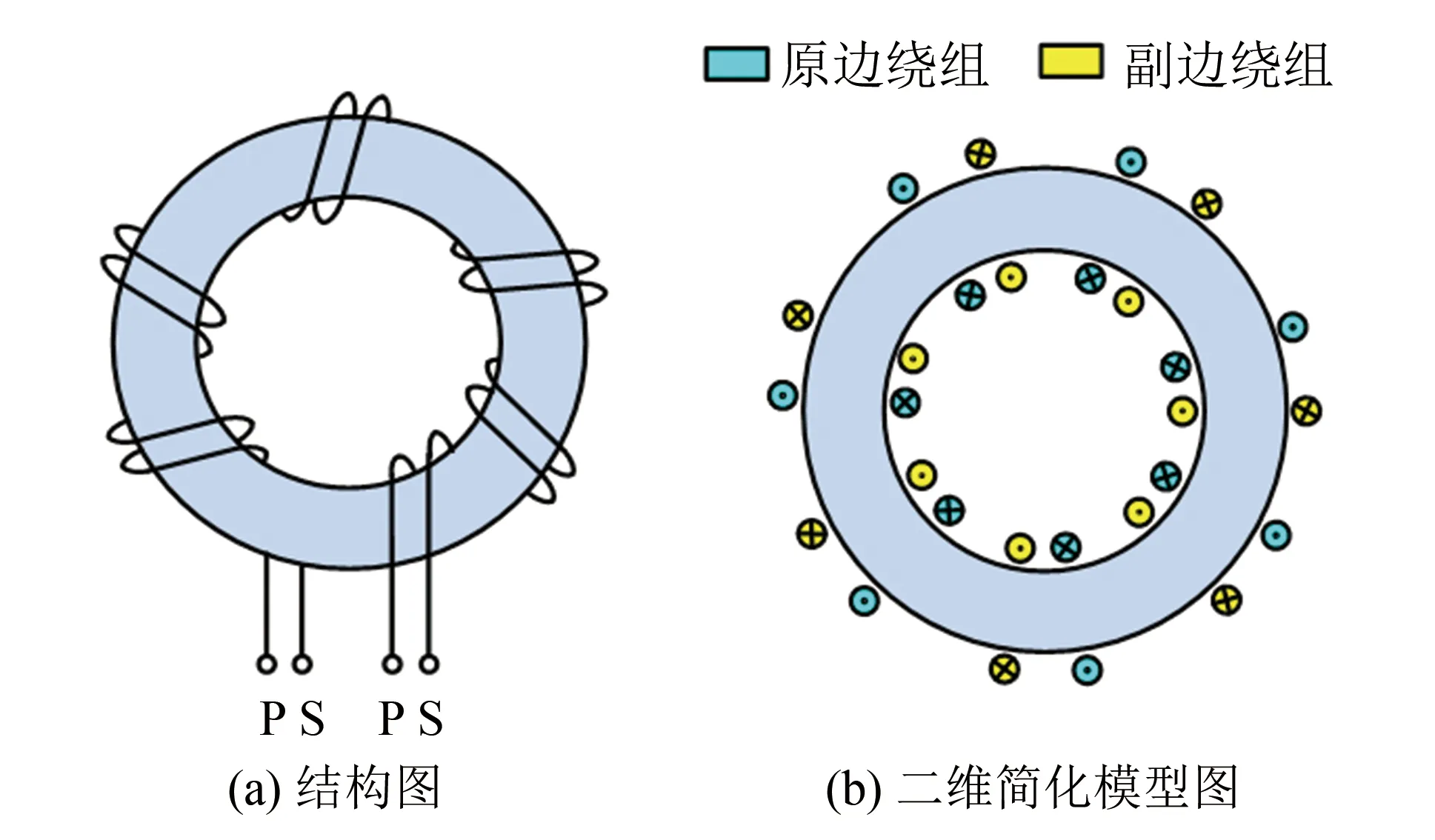
图1 环形空心电感结构图和二维简化模型图

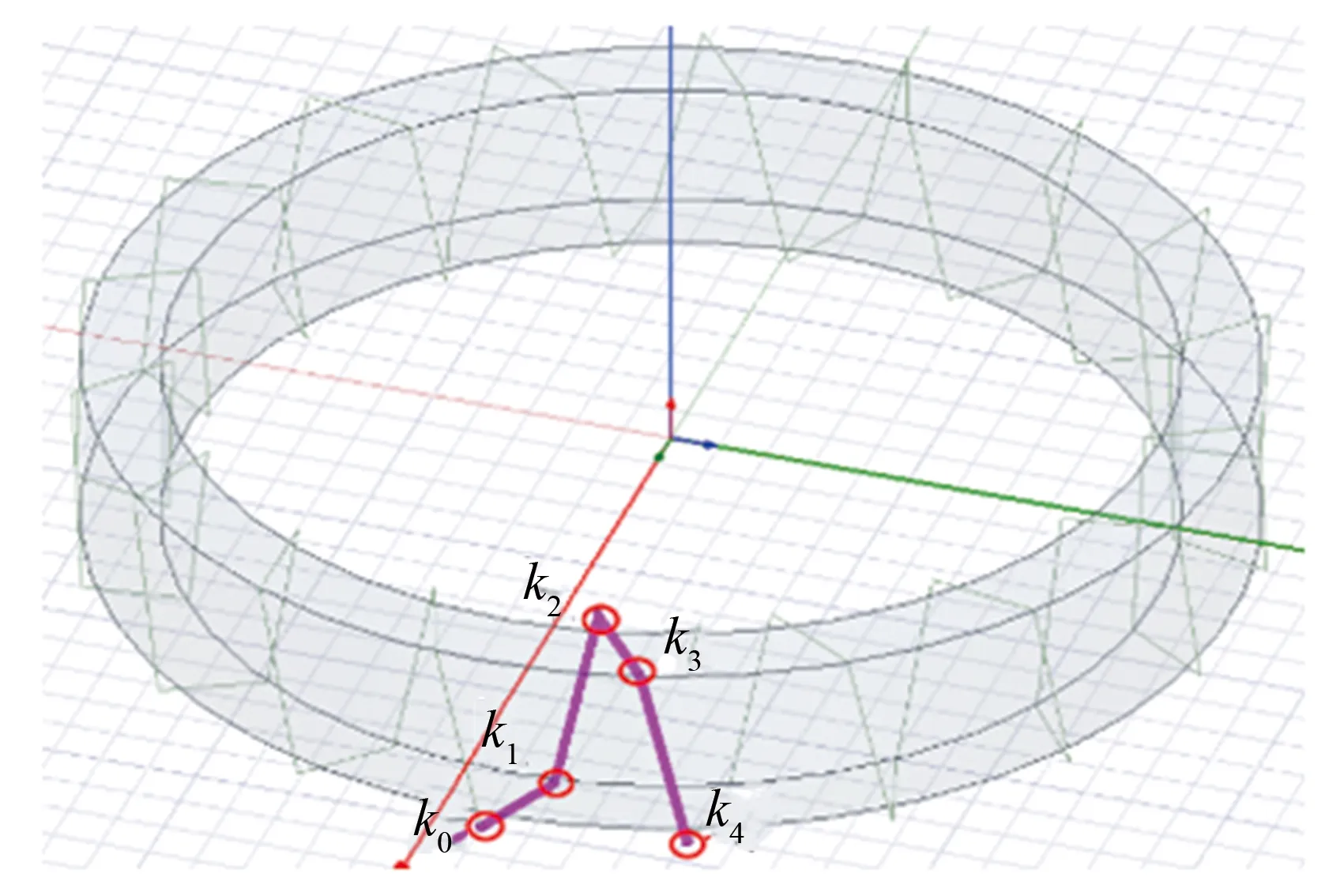
图2 单匝绕组中心回路示意图

此时单匝线圈的第i段线段方程可表示为：

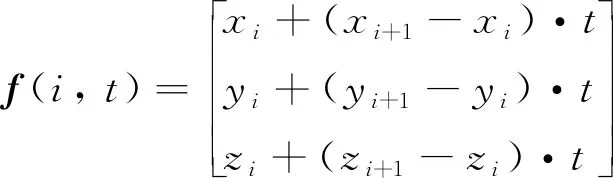
(2)

其中:t∈[0, 1]，i=0， 1， …, 4. 进一步地对单匝线圈方程作沿Z轴的旋转变换， 将式(2)乘上旋转变换矩阵后， 得到沿Z轴旋转的任意单匝线圈方程:

(3)

其中：N为绕组总匝数；θ为第a匝线圈需要旋转变换的角度. 进一步得到绕组线圈方程的微分形式为:

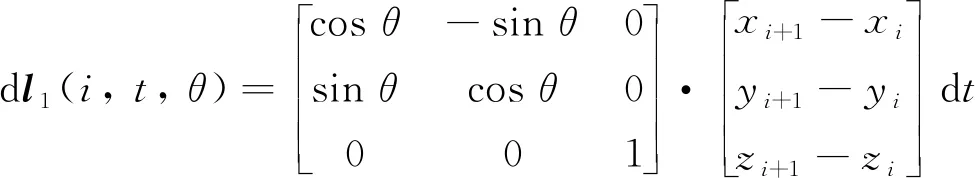
(4)

副边绕组中心回路方程l2的计算模型构建与原边类似， 最终根据式(1)得到空心电感原副边之间的互感计算公式:

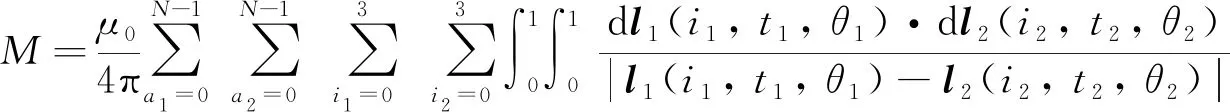
(5)

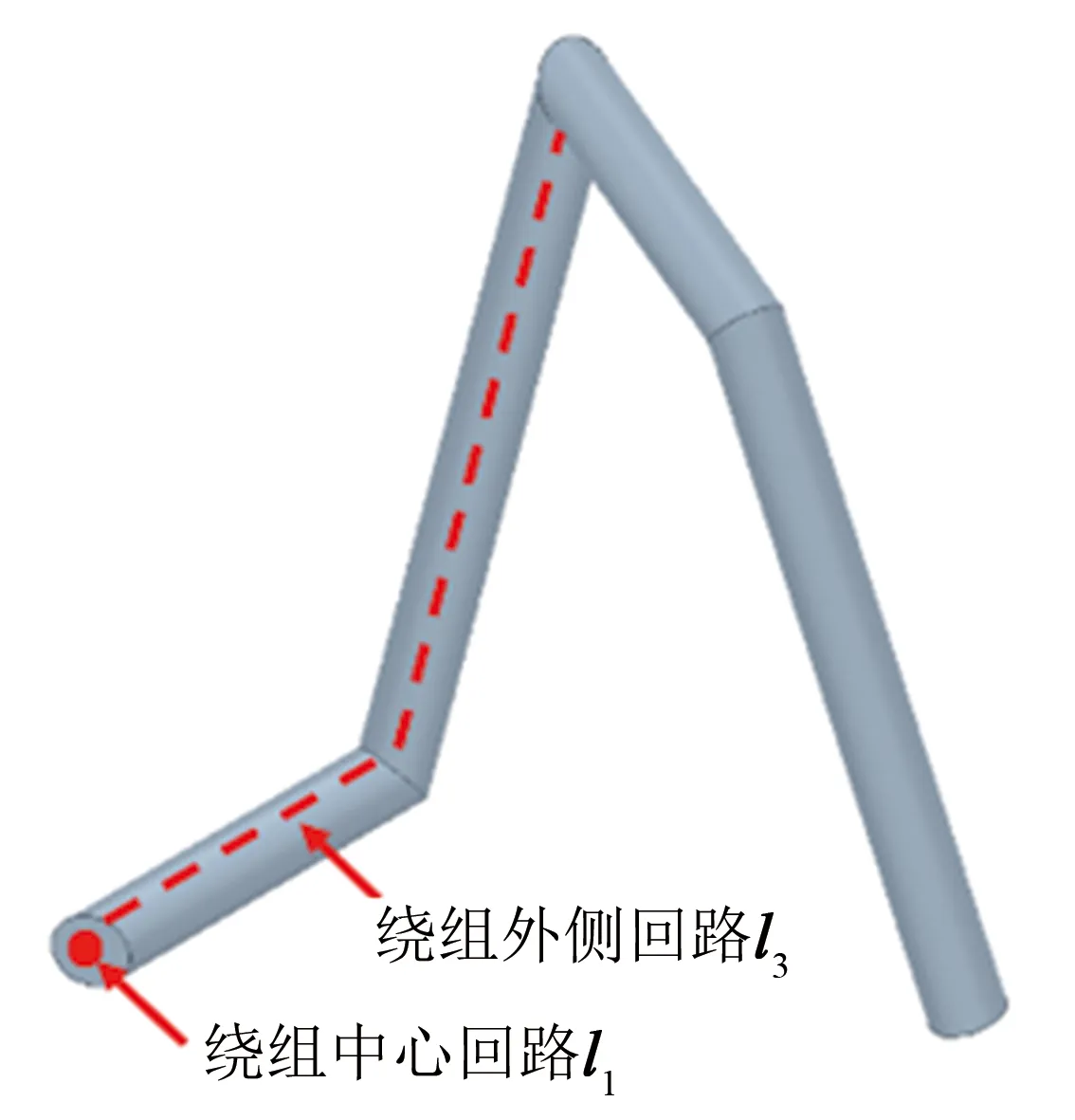
图3 单匝绕组外侧回路示意图

当利用式(1)求取原边绕组自感时，l1与dl1的表达式与式(3)、 (4)中相同. 而l3则为原边绕组外侧回路方程， 如图3所示.

根据绕组线径大小， 构建完整的原边绕组导线外侧回路方程l3及其微分形式dl3， 从而得到原边的自感值计算公式：

μ0d1·(8π)-1

(6)

在双股并绕情况下可认为原副边自感值相等， 故环形空心电感互感系数计算公式可表示为：

(7)

将式(5)和式(6)代入式(7)， 即可求解互感系数.

2 双股并绕空心电感互感系数及平行泄露磁场影响因素分析

在双股并绕的空心电感中， 可认为：

N1=N2；Lk1=Lk2=Lk

(8)

其中：N1、N2为原副边匝数；Lk1、Lk2为原副边漏感. 进一步将漏感模型与互感模型参数等效， 可得：

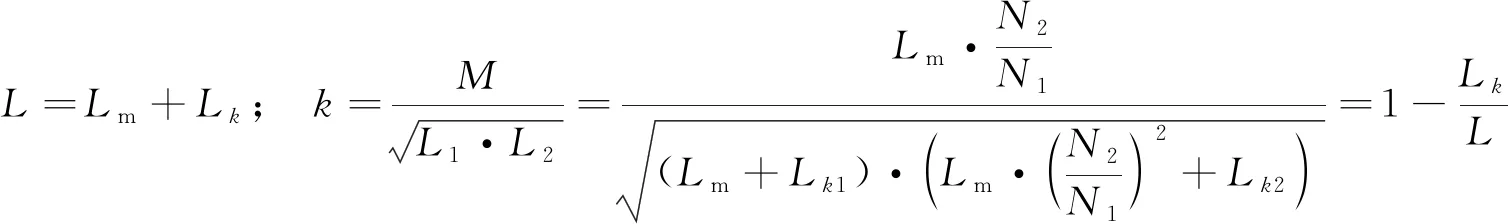
(9)

其中：Lm为激磁电感;L为原边、 副边总自感.

由式(9)可知， 在总自感相同的情况下， 互感系数越大， 漏感值越小. 本节主要以聂以曼公式和有限元仿真软件作为分析工具， 讨论绕组匝数和磁心尺寸对双股并绕空心电感互感系数和平行泄露磁场的影响.

2.1 绕组匝数对互感系数及平行泄露磁场的影响

在绕组均匀绕制的前提下， 绕组匝数决定了绕组间距和疏密程度， 这将决定主磁通和漏磁通分布， 并进一步影响互感系数. 利用式(5)～(7)计算内径为50 mm， 外径为80 mm， 线径为0.45 mm的双股并绕环形空心电感， 当匝数分别为9、 18、 36、 54、 72、 90匝时的互感系数. 改变匝数的同时改变电感高度, 分别为7.896、 3.080、 1.000、 0.483、 0.283、 0.184 m， 以保持总自感值不变. 不同匝数空心电感互感系数的计算结果与仿真结果如图4所示. 由图4可知， 二者基本吻合， 验证了该互感系数计算模型的准确性. 互感系数随着绕组匝数的增加而增加.

进一步研究其平行泄露磁场， 利用有限元仿真软件比较不同匝数空心电感在线段S1=50 mm上的平行泄露磁通密度， 如图5所示. 对不同匝数空心电感分别施加4.00、 2.00、 1.00、 0.66、 0.50、 0.40 A电流激励以保证主磁密大小相同， 主磁密的计算如下：

(10)

其中:μ0为真空磁导率，le为磁路有效长度，D2、D1分别表示电感磁心的内外直径.

仿真结果如图6所示， 可见绕组匝数越多， 平行泄露磁密越小， 且平行泄露磁密随着与电感外表面距离的增加而迅速减少.

图5 平行泄露磁场示意图

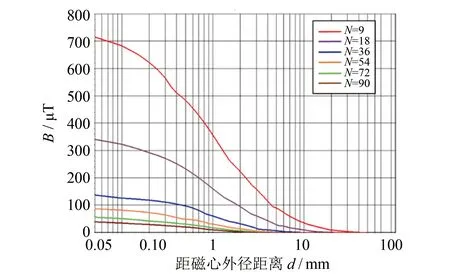
图6 平行泄露磁场随距离变化曲线

综上所述， 保持自感值相同， 增加绕组匝数可以提高双股并绕空心电感的互感系数， 减小漏感； 在主磁密相同的条件下， 增加绕组匝数可以抑制平行泄露磁通密度.

2.2 环形空心电感磁心尺寸对互感系数及平行泄露磁场的影响

改变环形空心电感磁心的内径、 外径、 高度将改变磁通分布. 利用聂以曼公式和有限元仿真软件计算线径0.3 mm， 匝数为18匝， 不同磁心尺寸的环形空心电感的互感系数. 改变内、 外径的同时调节高度， 以保证各尺寸条件下总自感值相等， 不同内、 外径下， 空心电感磁心高度如表1所示.

表1 保持自感值相同的各电感磁心尺寸

不同尺寸磁心空心电感的互感系数的计算结果和仿真结果对比如图7所示， 图8给出了不同尺寸磁心的绕组总匝长的变化曲线.

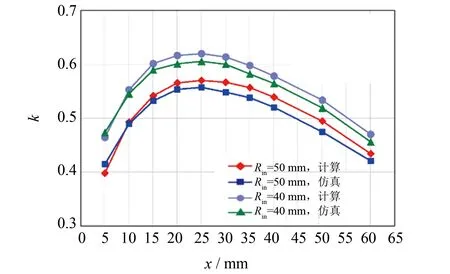
图7 互感系数随磁心尺寸变化曲线

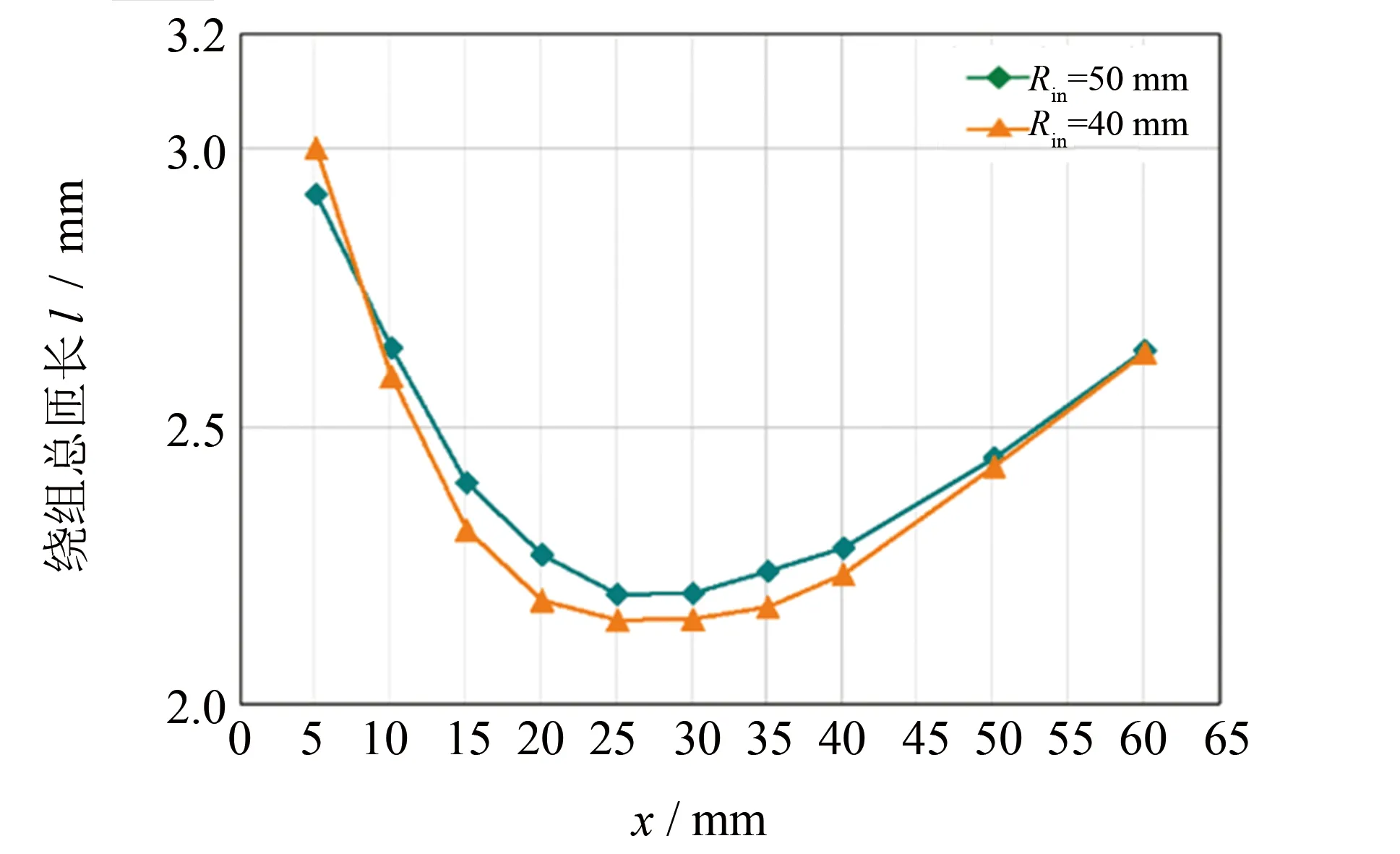
图8 绕组总匝长随磁心尺寸变化曲线

对比图7和图8可知， 当内径相同时， 随着总匝长的减小， 互感系数呈现上升趋势. 图中， 环宽为25 mm时， 总匝长为最小值， 互感系数达到最大值. 这是由于绕组总匝长的减小导致了仅链过原边单匝绕组而不链过副边绕组的漏磁通减小， 使得漏感减小， 互感系数提高， 如图9所示.

当空心电感匝数足够多时， 其感值可通过下式计算得到.

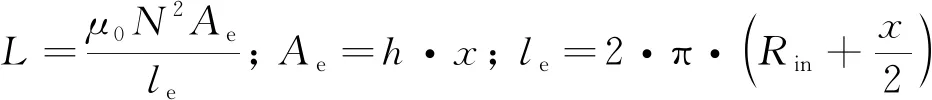
(11)

式中：h为电感高度；x为环宽，x=Rout-Rin.

可以得出， 在相同感值下， 当环宽为xmin时， 绕组总匝长最短.xmin的表达式为：

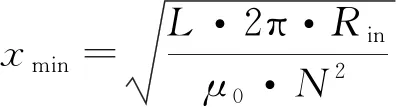
(12)

当环宽相同时， 内径小的空心电感互感系数高， 这是由于在相同匝数下， 内径更小的空心电感绕组绕制更加紧密.

进一步利用有限元仿真软件比较内径为50 mm， 不同外径空心电感沿线段S1=10 mm的平行泄露磁通密度. 由于不同外径的空心电感磁路有效长度不同， 根据式(10)对不同外径的空心电感分别给予0.87、 0.94、 1.00、 1.05、 1.11、 1.30 A电流激励以保证主磁通密度大小相同， 仿真结果如图10所示. 可见， 平行泄露磁密随着外径的增大而增大. 这是因为随着空心电感外径增大， 外层绕组匝间距增大， 导致平行泄露磁密增大.

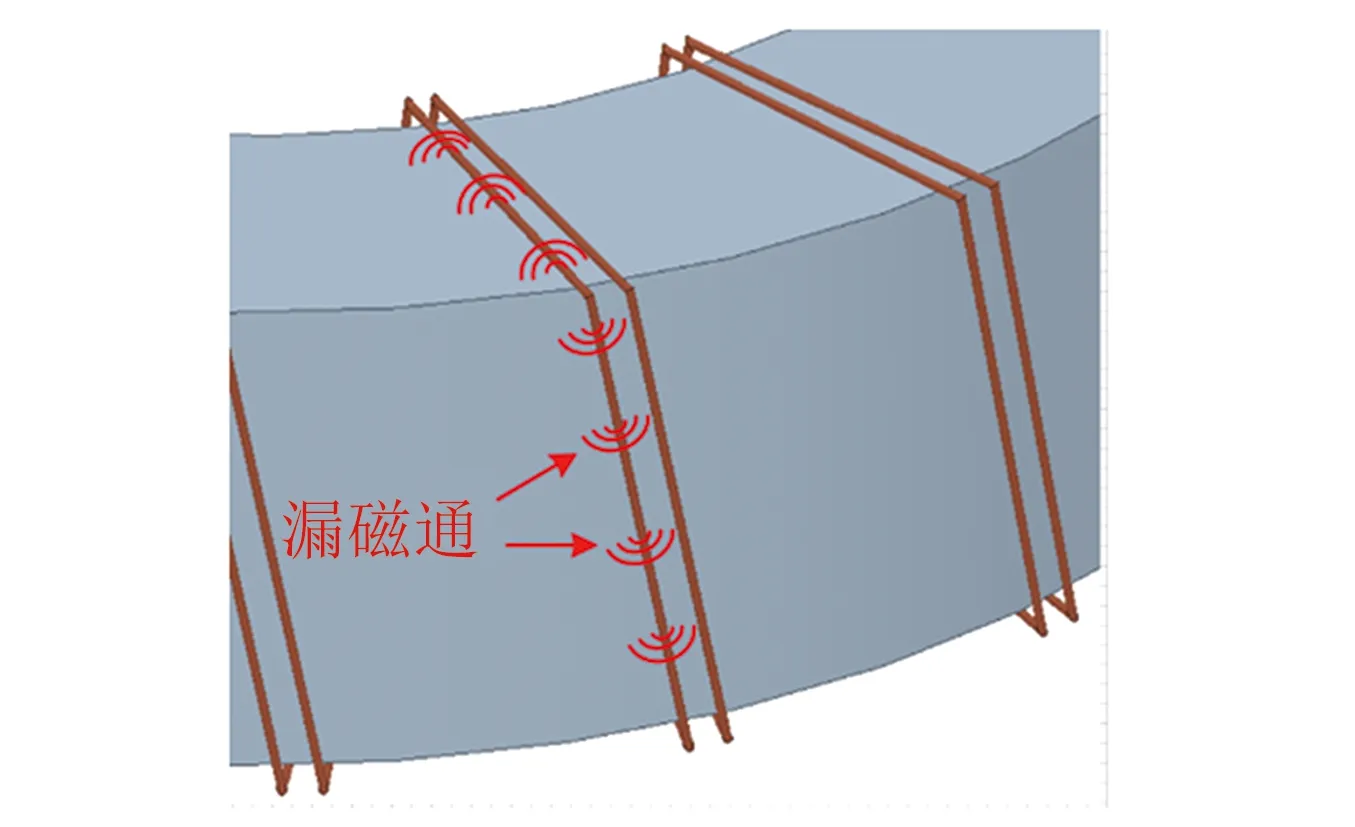
图9 匝间漏磁通示意图

图10 平行泄露磁场随距离变化曲线

综上所述， 在相同内径、 匝数和自感值下， 调整磁心尺寸使得绕组总匝长尽量小可以提高双股并绕空心电感的互感系数， 减小漏感； 在相同环宽、 匝数和自感值下， 减小内径可以提高绕组的紧密程度， 减小漏感； 在内径和主磁密相同的条件下， 增加空心电感外径会导致平行泄露磁通密度增加.

3 环形空心电感轴向磁场抑制方法分析

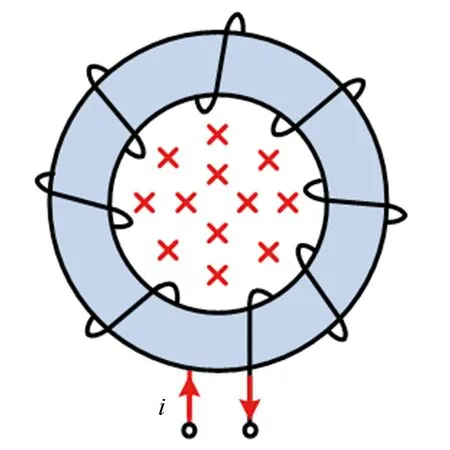
图11 环心空心电感轴向泄露磁场示意图

空心电感的磁导率为真空磁导率， 其电磁干扰问题十分严重. 由于环形空心电感的绕组沿着“环形”结构绕制， 因此， 无论匝数、 外径如何变化， 其轴向泄露磁场始终存在， 如图11所示.

对环形空心电感绕组的绕制方式合理优化， 可以有效抑制轴向磁场泄露. 提出三种轴向磁场抑制方案： 单匝返回匝抑制方案、 差分返回匝抑制方案、 分组绕制抑制方案， 各方案的绕组绕制方式如图12所示. 其中， 单匝返回匝抑制方案还可选择将返回匝置于电感顶部、 外径、 内径、 中心处， 如图12(d)所示.

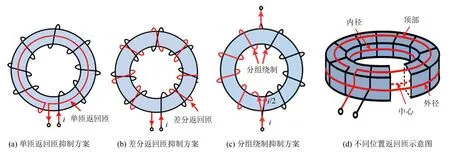
图12 轴向泄露磁场抑制方案

为比较三种方案对于轴向泄露磁场的抑制能力， 建立各绕组方案空心电感的理论计算模型， 并在空心电感上方构建一干扰回路， 如图13所示. 经过优化之后的环形空心电感与干扰回路互感系数越小， 则可认为该电感更不易受干扰回路影响， 对轴向泄露磁场的抑制效果越好.

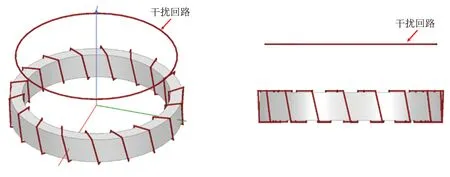
图13 干扰回路三维示意图

电感试样内、 外径分别为50、 60 mm， 高度为20 mm， 线径为0.45 mm. 普通电感与采用分组绕制抑制方案电感的主磁密计算式如下：

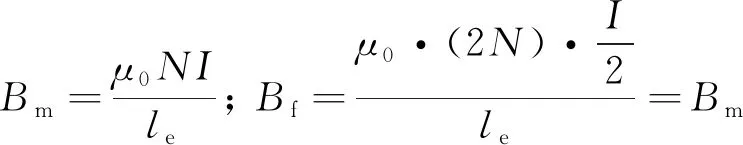
(13)

其中：Bm为普通电感的主磁密；Bf为分组绕制电感的主磁密.

由式(13)可知， 为保持各方案主磁密相同， 即感值相同， 分组绕制电感的匝数需为其他方案的两倍[18]， 故令匝数分别为18与36匝. 利用聂以曼公式计算各方案空心电感与干扰回路间的互感系数， 并利用有限元仿真软件进行验证. 计算结果与仿真结果对比如表2所示. 进一步利用有限元仿真软件分析空心电感上表面的磁通密度轴向分量Bz的分布， 仿真结果如图14所示.

表2 干扰回路与各抑制方案电感之间的互感系数

上述互感系数的计算、 仿真结果表明， 在单匝返回匝抑制方案中， 将返回匝置于电感中心处， 空心电感与干扰回路互感系数最小， 电感上表面的磁通密度轴向分量最小， 因此具有最好的轴向磁场抑制效果， 但在中心处绕制返回匝对制作工艺提出一定要求.

图14 空心电感上表面轴向泄露磁密分布图

在理想情况下， 采用差分返回匝的空心电感与干扰回路的互感系数为0， 电感上表面磁通密度的轴向分量仅存在于正、 反绕组间的交叉处， 呈正、 负分布， 整体轴向泄露磁场趋于0. 该方案具有十分良好的轴向泄露磁场抑制能力， 但对绕制工艺要求较高.

在理想情况下， 采用分组绕制的空心电感与干扰回路的互感系数也为0， 电感上表面磁通密度轴向分量在环心呈左右对称的正、 负分布， 整体轴向泄露磁场趋于0. 但由式(13)可知， 使用该方法绕制时， 需绕制两倍的匝数才能达到普通电感相应的感量， 这一方面使得在单层满绕时， 分组绕制电感值仅为普通电感的一半， 另一方面将增加空心电感的制作成本.

4 结语

由于空心电感的磁导率为真空磁导率， 因此存在双股并绕下互感系数较小以及严重的磁场泄露问题. 本研究采用聂以曼公式理论计算和有限元仿真软件分析空心电感互感系数和平行泄露磁场的影响因素， 得到如下2点结论：

1) 增加匝数， 提高绕组绕制紧密程度或减小绕组总匝长可提高双股并绕空心电感的互感系数， 减小漏感；

2) 在相同主磁密的条件下， 增加匝数可以减小平行泄露磁密， 而增大电感外径则会增大平行泄露磁密.

本研究提出三种轴向泄露磁场抑制方案， 并对比其抑制能力， 得到以下3点结论：

1) 单匝返回匝抑制方案中， 将返回匝置于电感中心处具有最好的抑制效果；

2) 差分返回匝抑制方案对轴向泄露磁场具有良好的抑制效果， 但却提高了绕制工艺的难度；

3) 分组绕制抑制方案对轴向泄露磁场具有良好的抑制效果， 但需要增加绕组匝数， 使得成本提高.