近地表空间梯度瞬变电磁粒子群优化反演研究

赖虔林，朱德兵，高 堤，朱 涵

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083；2.中南大学 有色资源与地质灾害探查湖南省重点实验室，湖南 长沙 410083)

1 引 言

瞬变电磁法(Transient Electromagnetic Methods，TEM)是利用不接地回线或接地线源向地下发送脉冲式一次电磁场，采用回线或接地电极观测该脉冲电磁场感应的地下涡流产生的二次电磁场时空分布，以达到探测地下地质目标体的一种电磁感应类方法[1,2]。在近地表瞬变电磁勘探中，常规瞬变电磁法受关断时间延迟、线圈自感及互感、一次场及大地二次场混合叠加等因素影响，瞬变早期阶段难以观测到有效信号，造成瞬变电磁法探测的“盲区”问题[3-7]。为有效解决此问题，朱德兵[8]提出一种瞬变电磁响应信号梯度测量方案，该方案能有效消除瞬变电磁一次场互感影响，使瞬变电磁早时段高精度观测成为可能。周光建[9]基于此方案深入研究空间梯度瞬变电磁法正演理论，得出这种观测模式显著提高信噪比和异常分辨能力的结论。基于上述研究基础，本文开展空间梯度瞬变电磁法一维反演研究。

一维瞬变电磁反演解释主要有两种方法。一种是烟圈反演方法，Nabighian[10]于1979年提出把向地下扩散的电流环近似等效为瞬变电磁响应，把随时间变化的瞬变电磁响应曲线转换为电阻率随深度变化的曲线以实现瞬变电磁的反演；另一种是基于正演公式的最优化方法，主要有高斯法、负梯度法、马奎特法等。具体过程是先给定初始模型参数，利用最优化方法对瞬变电磁响应数据进行拟合，进而不断修正模型参数，最终达到实测数据和正演数据某种意义下的最佳拟合，从而得到最佳反演结果。Nekut[11]于1987年提出一种中心回线瞬变电磁法的直接反演方法，其运算速度比最小二乘反演更快，能够估算电导率剖面，但精度不高。Christensen[12]于2002年提出基于自适应玻恩近似的快速近似一维反演算法，比普通非线性反演算法快约100倍。张继令等[13]于2007年将Occam反演技术应用到中心回线瞬变电磁测深数据的反演中，实现相对视电阻率的定性或半定量解释。薛国强等[14]于2008年总结瞬变电磁反演问题，叙述成像类反演方法主要有时频等效转换和波场转换两种方法。李永兴等[15]于2010年提出模型交替调整反演算法，并应用于航空瞬变电磁一维反演中，与Zohdy法相比，该方法具有更高精度。李明星等[16]于2014年将粒子群算法应用于瞬变电磁反演计算中，取得一定的反演效果。李展辉等[17]于2018年采用正则化Gauss-Newton迭代方法反演瞬变电磁数据。杨海燕等[18]于2018年针对圆锥形场源激发的瞬变电磁响应，采用阻尼最小二乘法实现矿井瞬变电磁反演。孙怀凤等[19]于2019年基于观测数据与模拟数据的L1范数建立目标函数，采用模拟退火非线性全局最优化方法实现瞬变电磁一维反演。Guo等[20]于2019年将SDM法应用于瞬变电磁资料的反演，通过引入先验信息，提高了反演精度，加快了反演过程。

本文首先开展空间梯度瞬变电磁法一维正演理论研究，基于Nabighian频率域响应公式并结合空间梯度观测模式，采用Gaver-Stehfest数字滤波算法、正余弦变换，推导出空间梯度瞬变电磁响应公式。随后针对近地表介质电性结构复杂、埋深小等特点，提出一种同时提高全局和局部搜索能力的基于反向学习策略的自适应混沌粒子群算法(Opposition-Based Learning Adaptive Chaotic Particle Swarm Optimization,OBL-ACPSO)。最后通过Rastrigin、Griewank两种测试函数，测试所提方案的性能。利用PSO算法和OBL-ACPSO算法分别对典型理论模型的无噪和含噪瞬变电磁数据进行反演，最终评价所提方案的适用性。

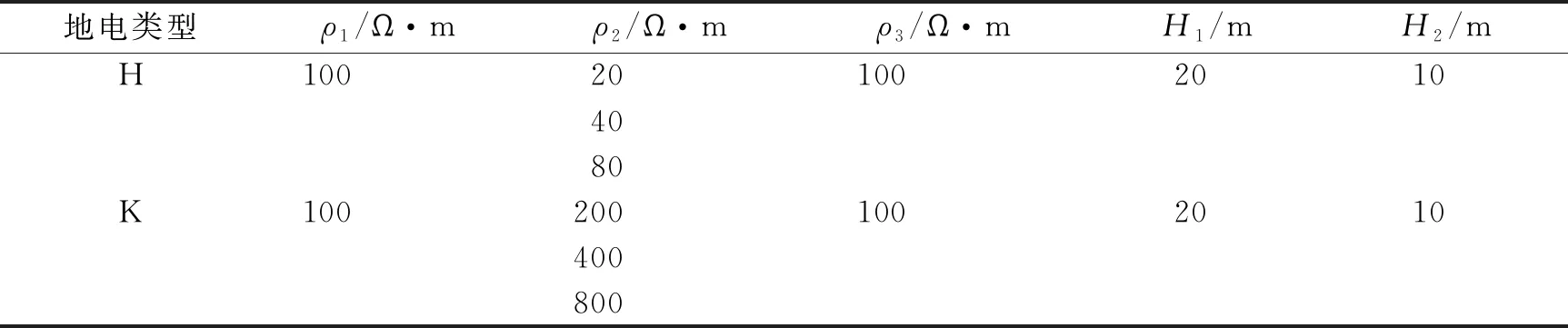
表1 模型参数-中间层电阻率变化

2 一维正演理论

根据瞬变电磁一次场空间分布的同轴等值性，空间梯度瞬变电磁测量模式利用以发射线圈为对称平面的上下平行共轴的两个相同接收线圈所得信号相减，消除瞬变电磁一次场及收发线圈互感的影响，实现TEM纯二次场响应观测，为近地表电性结构层高精度探测提供了技术支持。为了分析近地表空间梯度瞬变电磁观测模式的特点，建立一维层状介质模型。设地下半空间为n层介质组成，1～n层电阻率、厚度分别为ρi、Hi。建立柱坐标系，垂直向下Z为正，半径为a的圆回线位于地表以上h高度，两个同规格接收回线关于发射回线对称布置，上、下接收回线分别置于z1,z2位置，空间梯度回线装置见图1。

图1 空间梯度回线装置示意Fig.1 Schematic diagram of space gradient loop device

由Nabighian[21]研究TEM正演理论可知，当圆形发射回线位于距地面h高度、接收回线置于z位置组成中心回线装置时，所产生的垂向磁场响应为：

(1)

根据式(1)并结合空间梯度观测模式，可推导出空间梯度回线装置磁场垂直分量频率域响应为：

(2)

式(2)涉及到贝塞尔函数计算，采用Gaver-Stehfest线性数字滤波算法[22]求解，对于J1贝塞尔函数计算，本文选用一阶140点的滤波系数，相关参数可见文献[22]，本文不予具体列出。

计算出磁场垂直分量频率域响应，进行正余弦变换[23]，可求得空间梯度瞬变电磁时间域响应，二次场磁场分量对时间的导数及二次场感应电动势可表示为:

(3)

(4)

为了研究空间梯度回线装置和重叠回线装置对近地表介质的垂向探测能力，以H型、K型的三层介质地电模型为例，通过改变介质物性参数(表1、表2)，正演模拟两种装置模式的瞬变电磁响应，评价这两种装置的探测能力。表1与表2中H1、ρ1分别表示第一层的厚度和电阻率，H2、ρ2分别表示中间层的厚度和电阻率，ρ3表示第三层电阻率。空间梯度瞬变电磁装置参数设置为：发射回线半径1 m；距地面高度0.5 m；发射电流10 A；接收回线半径1 m，下方接收回线置于地面，上方接收回线置于距地面高度1 m位置；发射及接收线圈的匝数均为1。装置如图1所示。重叠回线装置置于地面，其它参数与空间梯度回线装置一致。

表2 模型参数——中间层厚度变化

图2 中间层电阻率变化条件下重叠回线和空间梯度回线异常曲线对比 (cd：重叠回线装置，td：空间梯度回线装置)Fig.2 Comparison of abnormal curves of overlapping loop and spatial gradientloop under the condition of resistivity variation of interlayer (cd: Overlapping loop device, td: spatial gradient loop device)

以均匀半空间下的瞬变电磁响应作为背景，计算两组模型在重叠回线装置和空间梯度回线装置的正演模拟结果，研究模型参数改变时的绝对异常变化和相对异常变化情况，结果见图2和图3，其相对异常计算表达式如式(5)。

(5)

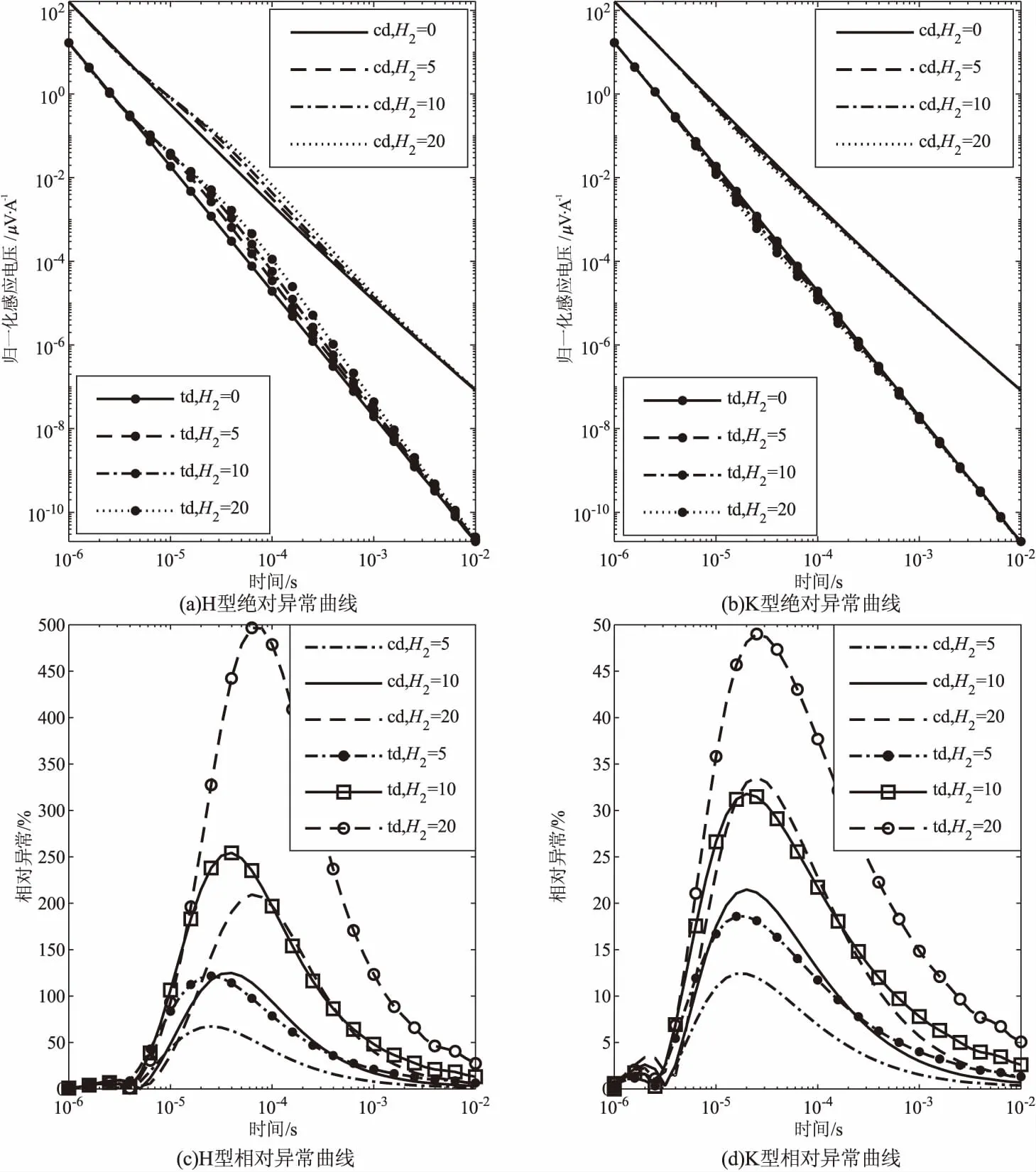
图3 中间层厚度变化条件下重叠回线和空间梯度回线异常曲线对比 (cd：重叠回线装置，td：空间梯度回线装置)Fig.3 Comparison of abnormal curves of overlapping loop and spatial gradient loop under the condition of Thickness variation of interlayer (cd: overlapping loop device, td: spatial gradient loop device)

式中：δi表示相对异常；Ai表示在物性参数变化时的瞬变电磁响应；A0表示ρ=100 Ω·m时的均匀半空间瞬变电磁响应。

由图2(a)、图2(b)和图3(a)、图3(b)可以看出，不论地电模型是H型还是K型，重叠回线装置的观测信号远大于梯度回线装置观测信号，表明前者在信号幅值上具有绝对优势。由图2(c)、图2(d)和图3(c)、图3(d)则可以看出，梯度回线装置测量的相对异常具有明显优势，尤其是对于1 ms内的早时段相对异常，重叠回线装置相对异常远不及梯度观测模式相对异常。这是因为瞬变早期阶段由于梯度回线装置压制一次场及收发线圈互感，而重叠回线装置信号采集包含瞬变电磁一次场信息，故相对异常信号提取中梯度回线装置更有优势；瞬变晚期阶段由于重叠回线装置测量一次场衰减完后的总二次场，而空间梯度装置测量纯二次场的差值，其幅值很小，所以重叠回线装置绝对值测量结果有优势。

H型和K型地电模型计算结果表明，空间梯度瞬变电磁观测模式对低阻介质体具有明显的异常分辨优势，且这种观测模式尤其适合在早时段(1 ms内)近地表测量，对电阻率变化反映灵敏度更高，有利于近地表快速、精确探测。同时考虑到近地表介质几何尺度变化大、结构复杂，其反演难度较大，故需要采取精确稳定的反演方案以实现近地表小尺度介质梯度瞬变电磁反演。

3 粒子群算法原理

3.1 基本原理

1995年Kennedy和 Eberhart提出了粒子群优化算法(Particle Swarm Optimization, PSO)[24]。在PSO算法中，每个“粒子”都会在搜索空间中飞行，并且存在一个速度决定其飞行方向和距离。算法初始化为一群随机粒子，在每一次迭代中，每个粒子根据个体历史最优位置pBest和当前种群粒子全局最优位置gBest来调整自身的速度和位置，以搜寻全局最优位置。根据式(6)和式(7)粒子更新自身速度和位置。

3.2 改进的粒子群算法

3.2.1 自适应惯性权重系数

在PSO算法寻优中，平衡全局搜索能力和局部搜索能力是有效求解最优解的关键。惯性权重w是PSO算法参数设置中至关重要的参数，w决定算法的全局与局部寻优能力。因此，在PSO算法中须选择合适w以精确高效地寻找全局最优解，文中根据粒子更新过程中变化的适应度值设置w。具体而言，根据式(8)确定自适应惯性权重因子(AIWF)。

(8)

式中：wmax、wmin分别表示惯性权重的最大值、最小值，本文取0.9、0.4；f表示粒子当前目标函数值；favg、fmin分别表示当前种群平均目标函数值和最小目标函数值。

根据式(8)，w随粒子当前目标函数值变化而变化。目标函数值小的粒子其惯性权重变化小，利于在可能的最优解附近精细搜索；目标函数值大的粒子其惯性权重变化相对大，其优势在于跳出局部极小值进而搜索新的区域。因此，自适应惯性权重因子为维持种群多样性和全局收敛能力提供一种良好途径。

3.2.2 反向学习策略

在算法进化后期，粒子多样性减少，导致收敛速度过快且过于早熟。为了克服这一问题，引入反向学习策略。即对PSO算法进化过程中产生的当前种群进行性能评价，选择目标函数值较差的前20 %粒子X，考虑其在搜索空间中对称位置的粒子X′性能。在多维搜索空间[ai,bi]中，假设粒子X(x1,x2,...,xn)为n维空间的粒子，则其反向位置X′(x′1,x′2,...,x′n)满足：

x′i=ai+bi-xi，i=1,2,...,n

(9)

式中：x′i表示某一维粒子xi在搜索空间中对称位置的粒子；[ai,bi]表示多维搜索空间。

反向学习策略同时搜索当前位置和反向位置粒子，评估两者性能，从中选择较优的粒子继续更新进化。这有效拓宽了粒子搜索范围，保持了种群多样性，增强了PSO算法全局寻优能力。

3.2.3 单维混沌局部搜索

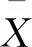
式中：x1∈(0,1)且x1∉{0.25,0.5,0.75};k表示当前混沌搜索次数;M表示最大混沌搜索次数;tpk,d表示第k次搜索第d维局部混沌产生的新解;t表示当前粒子群的迭代次数;Tmax表示粒子群的最大迭代次数。

采用单维混沌局部搜索方式，在PSO算法搜索的当前种群最优位置gBest附近进行局部搜索，当混沌局部搜索的最优新解优于当前位置最优解时，用最优新解代替当前位置最优解。通过这种方式可间接提高PSO算法的局部搜索能力，实现小范围内精细搜索。

3.3 算法测试

为检验OBL-ACPSO算法的寻优能力，选择Rastrigin、Griewank函数作为测试函数。这两个函数相似，有广泛分布的局部极值，属于典型的非线性复杂问题。利用上述两种测试函数检验OBL-ACPSO算法的性能，两种函数的二维表达式分别是：

上述两个测试函数存在全局最小值f(0,0)=0。图4为两个测试函数的三维图像，可以看出均存在大量局部极小值。

图4 测试函数三维图像Fig.4 3D image of test function

同时选择GA、PSO、CPSO作为对比算法，其中相关参数设置为：迭代次数200次；种群数50；学习因子c1=c2=2；惯性权重系数wmax=1.2，wmin=0.2。对于GA算法，Pc=0.7，Pm=0.05；对于PSO算法，采用线性递减的惯性权重系数；对于CPSO与OBL-ACPSO两种算法，采用自适应惯性权重系数，混沌局部搜索最大步数为10。为了测试算法的稳定性，对上述所有优化算法进行20轮运算，并取均值作为最优解，其寻优结果对比见表3，相应的目标函数曲线见图5。

表3 优化算法对测试函数的寻优结果对比

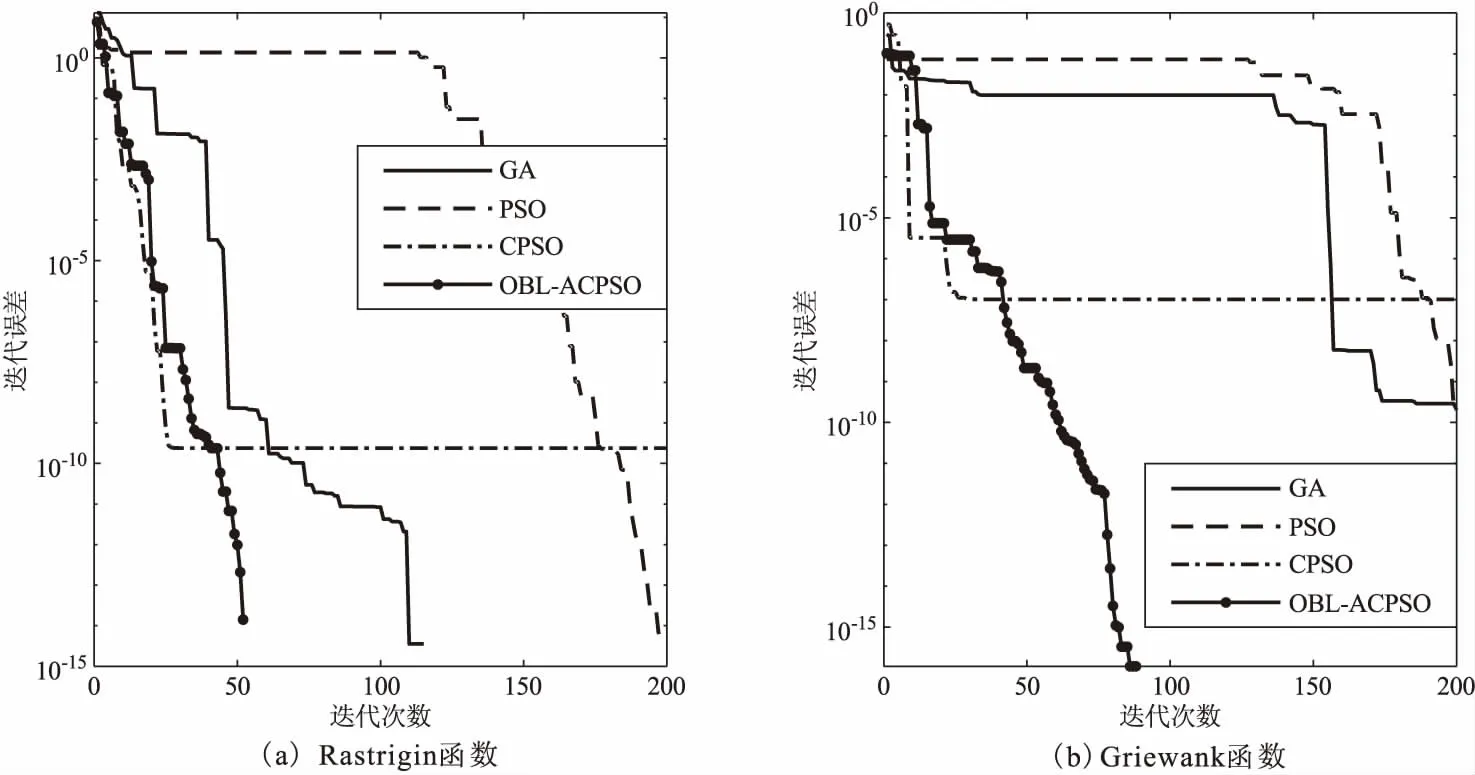
图5 四种优化算法对测试函数的寻优能力对比Fig.5 Comparison of four optimization algorithms for test function

由表3可知，对于上述两种测试函数，比较四种优化算法的最优解发现，OBL-ACPSO算法的寻优结果优于GA、PSO和CPSO算法的寻优结果；在20轮计算用时方面，GA算法较其它算法明显耗时，而对于PSO、CPSO和OBL-ACPSO三种算法的用时比较，T(OBL-ACPSO)>T(CPSO)>T(PSO)，主要原因是CPSO算法在PSO算法的基础上增加了混沌局部搜索方式，OBL-ACPSO在CPSO算法的基础上增加了反向学习策略。由图5可知，PSO算法收敛速度最慢，GA算法次之且存在多代未进化现象，CPSO与OBL-ACPSO两种算法较快，但CPSO算法在40次迭代停止，而OBL-ACPSO算法能够继续迭代寻优。经过以上对比，OBL-ACPSO算法相比较其它三种算法展现出更好的寻优能力，在计算用时相当的基础上，增强了全局和局部搜索能力，提升了全局收敛能力，保证了计算结果的精度，这为后续处理复杂寻优问题提供有效解决方案。

4 理论模型实验

基于上述改进的粒子群优化算法，将其应用于梯度瞬变电磁一维反演。在反演效果评价中，目标函数的选取至关重要。因此，针对梯度瞬变电磁数据动态范围大的特点，本文选取如下目标函数作为梯度瞬变电磁反演的评价准则：

(14)

设计实际勘查工作中，常见的三层介质地电模型，求解瞬变电磁二次场感应电动势理论值，并将OBL-ACPSO和PSO算法应用于空间梯度瞬变电磁一维反演中，通过对比反演结果，分析OBL-ACPSO的寻优能力。在反演过程中，反演模型参数的搜索范围设置为不小于理论参数值的±60%，其他反演参数为迭代次数80次，种群数50。空间梯度瞬变电磁装置参数设置为：发射回线半径1 m，距地面高度0.5 m;发射电流10A;接收回线半径1 m，下方接收回线置于地面；发射及接收线圈的匝数均为1。

4.1 三层介质地电模型

图6～图9分别为K型、H型、A型、Q型地电模型反演结果。从图6～图9的(a)图看出：对于三层介质地电模型反演，OBL-ACPSO算法比PSO算法效果更好，对层界面刻画明显，与理论模型层界面高度拟合；OBL-ACPSO算法感应电压拟合程度较高；图6～图9中的(c)图前60次反演迭代PSO算法下降较为缓慢，而OBL-ACPSO算法在30次迭代迅速下降至趋于稳定，迭代效率大幅度提升。

图6 K型地电模型反演结果对比Fig.6 Comparison of inversion results of K-type geoelectric model

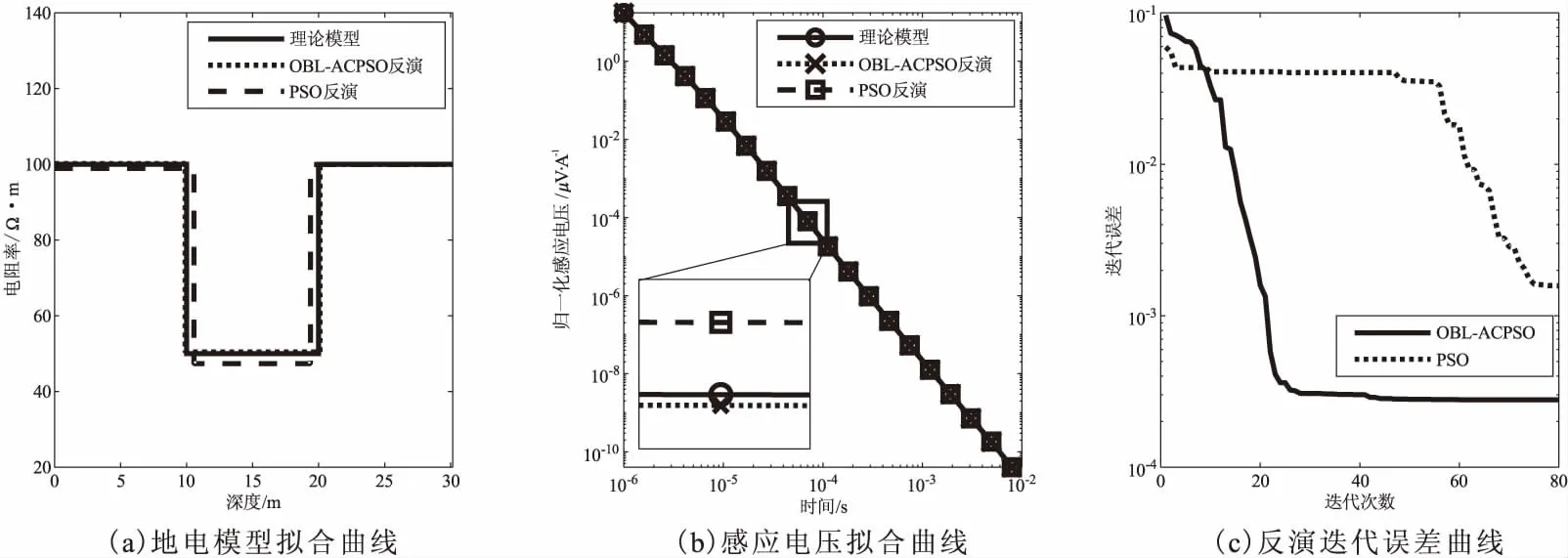
图7 H型地电模型反演结果对比Fig.7 Comparison of inversion results of H-type geoelectric model

图8 A型地电模型反演结果对比Fig.8 Comparison of inversion results of A-type geoelectric model

图9 Q型地电模型反演结果对比Fig.9 Comparison of inversion results of Q-type geoelectric model

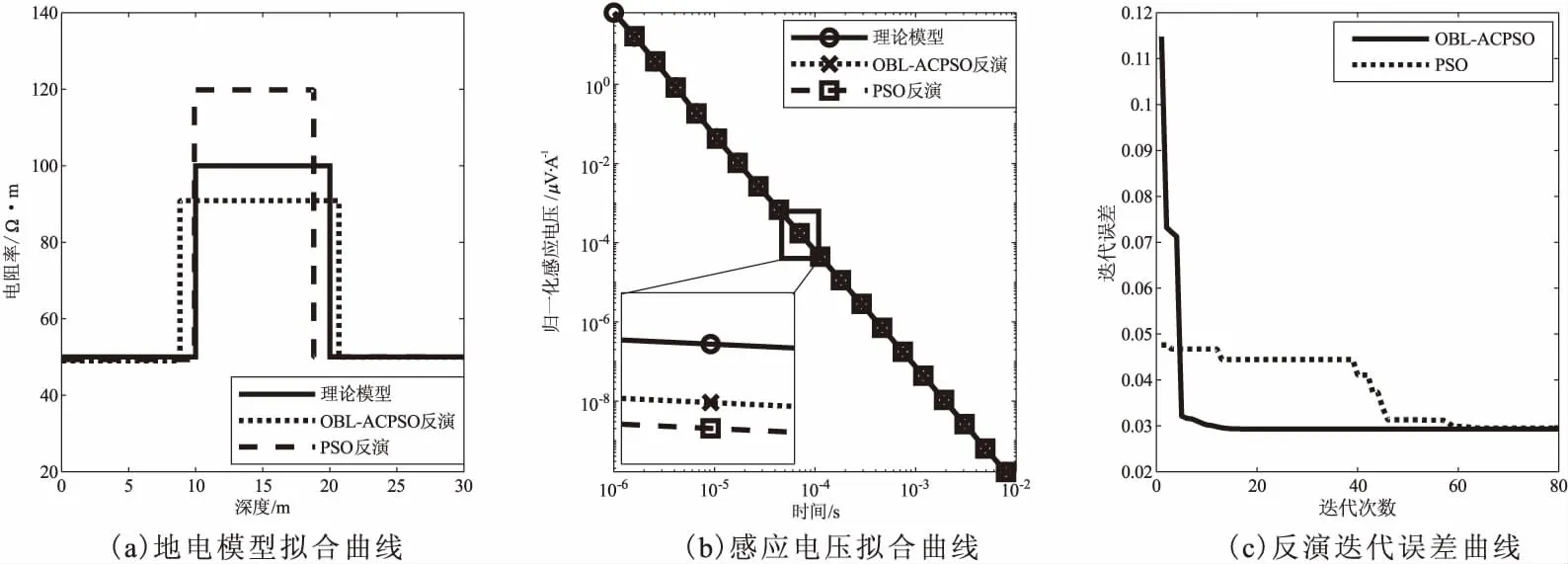
图10 K型地电模型含5 %高斯噪声反演结果对比Fig.10 Comparison of inversion results of K-type geoelectric model with 5 % Gaussian noise

图11 H型地电模型含5 %高斯噪声反演结果对比Fig.11 Comparison of inversion results of H-type geoelectric model with 5 % Gaussian noise

4.2 含噪声三层介质地电模型

瞬变电磁实测数据往往含有噪声干扰，为了测试OBL-ACPSO算法对含噪声瞬变电磁数据的反演性能，对典型三层地电模型正演得到的瞬变电磁感应电压数据加入5 %的高斯噪声，并对含噪声的瞬变电磁感应电压数据进行PSO、OBL-ACPSO算法反演分析。图10～图13给出反演结果，可以看出：图10～图13的(a)图地电模型图中，OBL-ACPSO反演结果更接近于理论模型，优于PSO反演结果，表明其抗干扰能力更强。图10～图13的(b)图感应电压拟合曲线中展示了0.07 ms时刻的拟合效果，采用OBL-ACPSO算法反演得到的地电参数，再通过正演得到感应电压曲线拟合效果优于PSO算法；图10～图13的(c)图迭代误差曲线图中，两种算法的最小拟合误差值趋于一致，但对于达到该值的最小迭代次数对比中，OBL-ACPSO算法低于20次，而PSO算法高于60次，说明OBL-ACPSO算法拟合误差下降速率较快，迭代效率更高。

图12 A型地电模型含5 %高斯噪声反演结果对比Fig.12 Comparison of inversion results of A-type geoelectric model with 5 % Gaussian noise

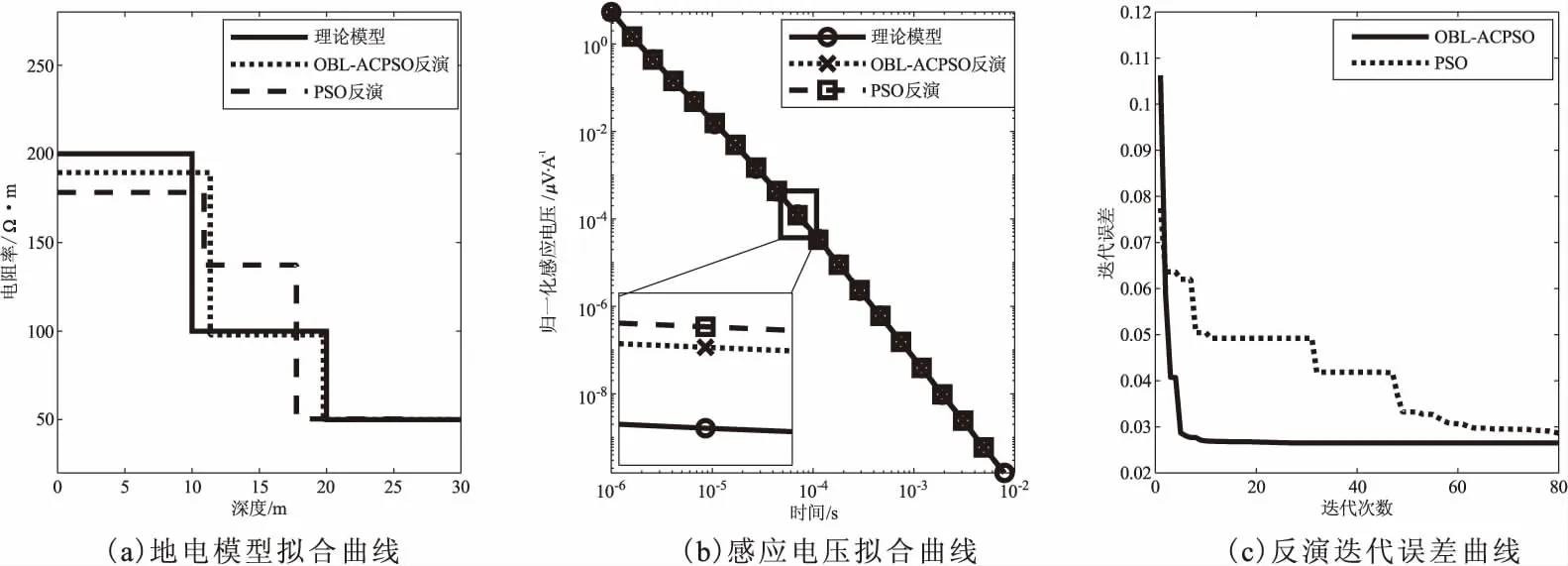
图13 Q型地电模型含5 %高斯噪声反演结果对比Fig.13 Comparison of inversion results of Q-type geoelectric model with 5 % Gaussian noise

根据上述无噪与含噪声瞬变电磁感应电压数据反演结果，OBL-ACPSO算法寻优能力较PSO算法好，计算精度更高，反演结果电阻率曲线形态与理论模型相符合，尤其表现在对目标体层界面的高分辨刻画，具有一定的分层效果。对于加入一定高斯噪声情况下的瞬变电磁感应电压数据，反演结果依然和理论模型曲线形态一致性较好，表现出良好的抗噪声能力。

5 结 论

1)空间梯度瞬变电磁法一维正演理论研究表明，空间梯度瞬变电磁观测模式在1 ms内的早时段记录具有明显优势，对近地表30 m深度范围介质的地电参数变化反映较为灵敏。

2)近地表介质几何尺度变化大、结构复杂，精确反演难度增大。OBL-ACPSO算法明显增强粒子寻优能力，提高了计算精度，抗噪性能突出，反演结果能够有效反映地电模型曲线形态，为近地表空间梯度瞬变电磁数据实现小尺度介质快速反演解释提供了新算法。

3)近地表30 m深度范围内介质结构地电参数纵横向变化大，实际工程中要将算法投入应用，还需要对梯度瞬变电磁响应接收数据进行更精细地剖析，确认1 ms早时段响应信号来自于TEM涡流响应或仅与介质电阻率这一物性参数关联。