电磁平衡头自锁力矩有限元分析及试验研究*

梁警威，刘保国*，申会鹏，梅俊伟

(1.河南工业大学 机电工程学院，河南 郑州 450001；2.河南省超硬磨料磨削装备重点实验室，河南 郑州 450001)

0 引 言

随着旋转机械向高速化和智能化方向发展，主轴高速下动态性能越来越不可忽视。电主轴具有转速高、结构紧凑及动态性能好的优点，在磨床上已被广泛使用[1]。在磨床磨削加工时，砂轮的磨损和切削液的分布不均匀，会导致砂轮质量分布的不平衡。高速下微小的不平衡量都会引起极大的离心力和系统振动，进而导致磨削精度下降、加工质量不稳定等现象。

为解决此类问题，需对砂轮-电主轴系统进行动平衡[2-4]。传统的线下动平衡技术需停机，且平衡精度低，严重影响了机床的加工效率和工件的加工质量，已不能满足现代化生产需求[5]。而线上的平衡方法具有不停机、平衡精度高、平衡时间短等优点，已经成为最具发展潜力的平衡技术[6，7]。

国外以德国HOFMANN公司[8]、美国SCHMITT INDUSTRIES公司[9]和意大利MARPOSS公司[10]代表的电磁平衡系统产品已在高端机床上得到了应用，但因其价格过于高昂，目前还尚未得到大量的推广。且由于该类产品现阶段还处于技术垄断阶段，其内部细节公开较少。

国内从20世纪90年代末开始，多位学者相继开展过这方面的研究，并试制出了多种电磁式主动平衡系统[11-13]。其中，电磁主动平衡头作为产生平衡质量的关键部件，其内部质量块在高速旋转状态下的自锁力矩峰值决定了平衡系统的可靠性。自锁力距由永磁体和齿盘相互作用形成，目前关于电磁平衡头自锁力矩的研究，主要集中在永磁体和齿盘的气隙[14]、齿盘的厚度和材料[15]、永磁体的尺寸和型号[16]等参数上；研究方法则主要为有限元分析等。

本文在已有研究的基础上，采用有限元分析的方法，研究永磁体和齿盘气隙长度改变时自锁力矩的变化规律。

1 实物及其分析模型

电磁主动平衡头机械结构主要包括动环和静环，自锁结构安装在动环上，永磁体N、S极交替排布安装在配重盘上，并夹在两个齿盘中间，每相邻的两个永磁体和对应齿盘上齿构成自锁磁路。

为增大自锁力矩对其相关结构[17]进行了改进，笔者重新进行了设计，忽略实物中的倒角、螺纹孔和不锈钢支撑件等对磁路影响较小的工艺特征，简化后得到了磁路的三维模型。

自锁磁路的几何模型(12齿)如图1所示。

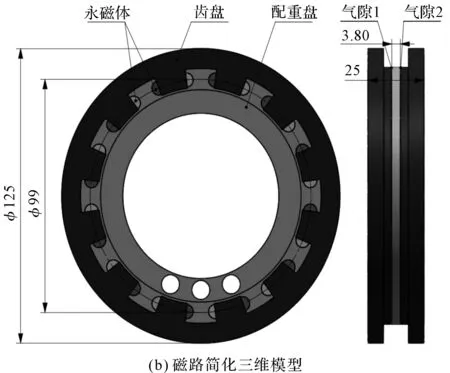
图1 自锁磁路的几何模型(12齿)

图1中，各个零件结构尺寸、材料等参数如表1所示。

表1 结构尺寸与材料

考虑到气隙太小时加工难以保证，且旋转过程中永磁体和齿盘易发生摩擦，因此，此处的气隙最小值取0.1 mm。

2 有限元分析

在自锁磁路三维模型基础上，笔者利用ANSOFT MAXWELL-3D平台进行自适应网格划分[18]，施加磁场自然边界条件，调用其瞬态求解器分析计算。永磁体和齿盘相对转速为12.5 r/min，求解步长为1 ms，即计算出每隔永磁体和齿盘每隔0.075°转角下扭矩值，根据瞬态值结果得出自锁力矩峰值。

经过多次仿真计算可得出气隙尺寸从0.1 mm到0.5 mm自锁力矩峰值变化规律，如图2所示。

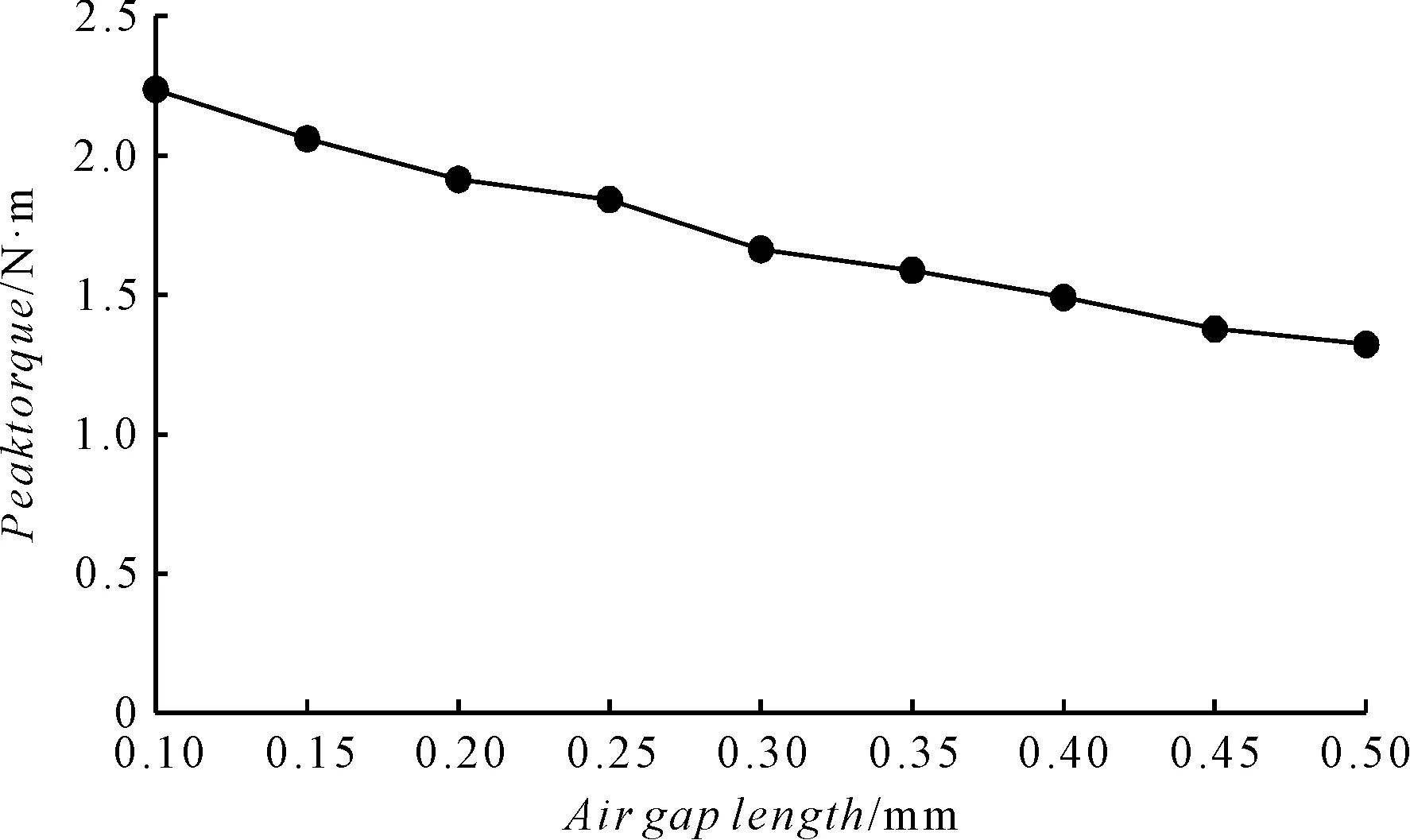
图2 不同气隙长度下自锁峰值仿真曲线

图2的结果表明：自锁力矩峰值在气隙为0.1 mm时取得最大值2.24 N·m；随气隙长度的增大呈类似指数函数减小，在气隙从0.1 mm增大到0.5 mm时，力矩峰值减小了41%。

3 试验验证

3.1 试验原理

自锁力矩峰值测试原理如图3所示。

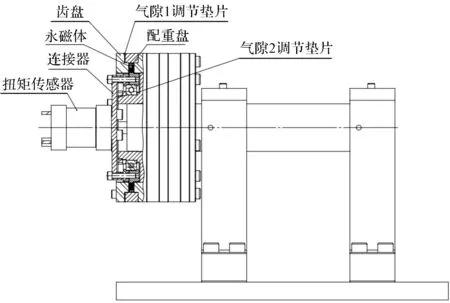
图3 自锁力矩测试原理

从图3可以看出：两个齿盘固定，永磁体安装在配重盘上，配重盘通过连接器和扭矩传感器连接，通过转动传感器左端测试一个步距角内磁路的自锁力矩峰值。

气隙调节垫片如图4所示。

从图4可以看出：气隙1调节垫片安装于两齿盘中间挡圈处，气隙2调节垫片安装于轴承内挡圈和动环基体之间，通过增减垫片数量调节气隙长度。

图4 气隙调节垫片(单片厚度0.05 mm)

3.2 试验

为了测量气隙变化时自锁力矩峰值的变化规律，笔者搭建了试验平台。

该试验平台主要包括：电磁平衡头动环、动环支撑附件、气隙调节垫片、连接器、扭矩传感器、扭矩信号变送器、开关电源、9215模拟信号采集模块、cDAQ9178信号采集平台、NI软件平台。

自锁力矩测试平台实物图如图5所示。

图5 自锁力矩测试平台

采集程序如图6所示。

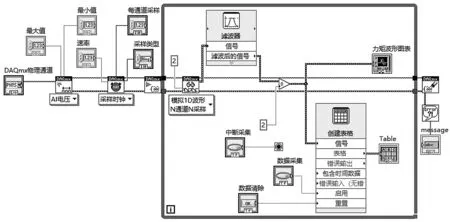
图6 采集程序

笔者通过垫片数量改变气隙长度后，测得的不同气隙下力矩峰值如图7所示。

图7 不同气隙长度下自锁峰值试验曲线

图7结果表明：自锁峰值在气隙为0.1 mm时，取得最大值1.95 N·m，随气隙长度增大呈类似指数函数减小；在气隙从0.1 mm增大到0.5 mm时，力矩峰值减小了42%。

4 结果分析

笔者将有限元分析的结果与试验的结果进行了对比，如图8所示。

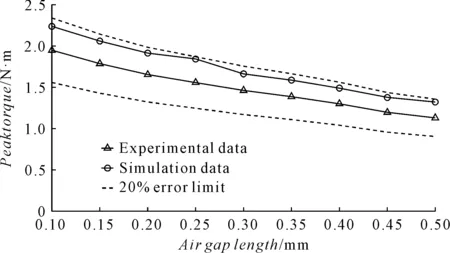
图8 自锁峰值仿真和试验对比

图8的结果表明：力矩峰值随气隙长度的增大而减小，有限元分析结果和试验测量结果变化趋势一致。

由于永磁体边缘镀层间接增大了气隙及端面圆角减小了截面积，且制造中存在加工误差、材料材质不均匀等因素，试验测量值小于有限元分析值，但误差在20%误差限以内，满足一般工程要求。

5 结束语

在已有研究的基础上，笔者采用有限元分析的方法，研究了永磁体和齿盘气隙长度改变时自锁力矩的变化规律；并搭建了试验平台，通过试验测得的数据验证了有限元分析结果的有效性。

结论如下：

(1)自锁力矩峰值随气隙长度的增大呈类指数函数减小，气隙长度从0.1 mm到0.5 mm时自锁峰值减小40%以上，在实际设计中在保证永磁体和齿盘不发生摩擦的情况下尽量减小气隙长度；

(2)试验测量值略小于有限元分析值，但误差在20%以内，通过试验验证了有限元分析的有效性，为相关分析计算提供了参考。

该研究结果可为电磁平衡头的研发设计提供重要依据，为装配调试提供参考。