SG-VMD-SVD的信号去噪方法研究

李 宏, 褚丽鑫, 刘庆强, 路敬祎, 李 富

(1. 东北石油大学 a. 电气信息工程学院; b. 黑龙江省网络化与智能控制重点实验室; 2. 大庆钻探工程公司 钻井一公司, 黑龙江 大庆 163318)

0 引 言

在油气管道泄漏检测中, 实际采集的油气管道泄漏信号具有非平稳性以及信号混合性的特点, 同时实际信号中含有大量的噪声, 然而经验模态分解(EMD: Empirical Mode Decomposition)算法和变分模态分解(VMD: Variational Mode Decomposition) 算法都适用于分析处理非平稳信号, 并可对油气管道泄漏检测中所采集的信号进行处理[1-3]。为处理非线性平稳信号, Huang等[4]提出了一种自适应的经验模态分解(EMD)算法, EMD是一种将时域信号按频率尺度分解的数值算法, 其在信号分解时容易产生模态混叠现象, 从而导致分解的本征模态函数(IMF: Intrinsic Mode Functions)分量失真。为解决EMD模态混叠现象, Dragomiretskiy等[5]提出变分模态分解(VMD), 它是一种新的多分辨率变分模态分解算法, 也是一种完全非递归的自适应信号分解方法, 它不仅能将信号中的噪声良好地分离, 而且可有效地抑制信号分解中的模态混叠,克服了EMD算法的局限性。VMD虽然能很好地抑制模态混叠现象, 也能处理非线性信号, 去除信号中的噪声, 但为了提高VMD的去噪效果, 区分信号分量和噪声分量也是重要一步。

Ma等[6]提出了一种VMD和豪斯多夫距离相结合的去噪法, 该方法先通过VMD分解, 然后计算信号经VMD分解后各IMF分量与采集到的泄漏信号的豪斯多夫距离选取有效分量, 对选取的有效IMF分量进行重构, 从而达到去噪效果。Lu等[7]提出了一种VMD和改进的巴氏距离的去噪方法, 信号经VMD分解为若干个模态, 然后利用改进的BD(Bhattacharyya Distance)优选模态, 将有效模态进行重构得到去噪后的信号。Zhang等[8]提出了基于VMD-WT的联合去噪方法, 信号经过VMD分解为若干个模态, 然后用WT算法对每个IMF进行二次去噪, 使各IMF的周期特征更加明显。罗小燕等[9]提出了VMD与时域奇异值分解联合降噪方法, 通过互相关系数阈值确定敏感分量, 再将敏感分量利用奇异值分解进行降噪处理, 得到最终的降噪信号。赵艳菊[10]提出了频域奇异值分解降噪法, 先将时域序列转换为频域序列, 然后经过奇异值分解, 重构, 最后通过傅立叶逆变换转化为时域序列, 完成对信号的降噪, 提高了降噪性能指标。赵凯凯等[11]提出一种基于频域奇异值分解的LPI雷达信号降噪, 验证了频域奇异值分解降噪能力优于时域奇异值分解, 且证明了降噪效果与噪声强度有关。

鉴于此, 笔者提出一种基于SG-VMD与频域SVD(Singular Value De-noising)的信号降噪方法, 首先, 将信号通过SG(Savitzky-Golay)平滑滤波进行预处理, 然后将滤波后的信号经过VMD分解, 利用曼哈顿距离增量区分信号分量和噪声分量, 考虑到噪声分量中也有部分有用信息, 因此对噪声分量进行频域奇异值降噪, 最后将滤波后的分量与信号分量进行重构, 完成对信号的降噪处理过程。

1 SG-VMD-SVD去噪方法的相关理论

1.1 SG平滑滤波

Savitzky-Golay平滑滤波法被普遍应用于数据流的平滑降噪, 主要是通过移动窗口在时域中利用最小二乘法拟合时域中的信号序列, 能在有效去除噪声的同时不改变原信号的形状和宽度[12]。构造一个以xi为中心包含2M+1个采样点的窗口数组, 而后构造一个P阶多项式q(n)拟合该数组

(1)

定义函数

(2)

当式(1)取得最小值时拟合效果最好, 而后通过移动该窗口数组即可得到原始数据的所有拟合点。在拟合过程中, 过于偏离正常趋势曲线的噪声部分被舍掉, 起到了平滑滤波的作用, 从而对信号实现降噪处理[13]。对信号进行平滑滤波后得到的信号如下[14]

(3)

其中f(i)为滤波后的信号,h(k)为平滑滤波器的抽样响应,y(x)为原始信号中的一组数据,x=-N,…,0,…,N。

1.2 VMD

VMD适用于处理非线性信号, 其分解过程实际就是一种对变分问题的求解过程, 是将一个信号f分解成K个模态函数uk(t), 使每个模态的估计带宽之和最小。其具体分解过程[5]如下。

1) 对每个模态函数uk(t)采用Hilbert变换计算相应的解析信号, 进而得其单侧频谱

(4)

2) 对每个模态函数uk(t), 通过与其对应的中心频率的指数项混叠, 将每个模态的频谱调制到相应的基带

(5)

3) 由解调信号的高斯平滑法估计出各模态信号带宽, 即梯度平方范数, 进而求解带约束条件的变分问题, 其约束变分表达式为

(6)

其中{uk}={u1,…,uk}为分解获得的K个IMF分量; {ωK}={ω1,…,ωK}为各分量的频率中心； *为卷积, ∂t为对函数求时间t的导数；δ(t)为单位脉冲函数。

4) 采用二次惩罚因子∂和拉格朗日乘法算子求式(3)的解, 将约束性变分问题变为无约束问题, 即

(7)

5) 采用交替方向乘子法解决以上变分问题, 通过交替更新uk,ωk以及λn+1寻求扩展拉格朗日式的鞍点, 此时变分问题的解为

(8)

6) 同理, 解得中心频率的更新方法为

(9)

1.3 频域SVD

在信号处理中, 对采样的时间序列{xi,i=1,2,3,…,N}, 若要应用奇异值分解方法, 需要构建一个重构n维相空间, 具体步骤参看文献[10], 经过相空间重构后, 一个一维向量构成一个m×n维的矩阵, 如下

(10)

其中Dm为相空间重构的一个矩阵,m为嵌入维数, 且m+n-1=N, 利用x(t)的采样序列做相空间重构, 获得Hankel矩阵Hm。在频域SVD理论中, 需要先将矩阵Hm做傅里叶变换, 得到一个新的频域序列的矩阵, 而后将新的矩阵进行SVD分解为

Hm=USVT

(11)

其中U和V分别为m×m阶和n×n阶正交阵,S为对角矩阵, 对角线元素α1,α2,…,αn即是Hm的奇异值, 且是按降序排列的。在一段含噪的信号中, 信号只贡献重构矩阵的前r个奇异值, 而噪声对奇异值的贡献是均匀的[11]。保存前r个包含信号特征的奇异值, 其他噪声贡献的奇异值置零, 代入式(11)中, 作SVD的逆过程

A0=US0VT

(12)

其中S0为去除小奇异值后的对角矩阵；A0为处理信号后的去噪矩阵。经傅里叶逆变换得到时域序列, 即为降噪后的信号。通过傅里叶变换可以突出信号的特征频率, 从而提高SVD的抗噪性。

1.4 曼哈顿距离

曼哈顿距离[15](MD: Manhattan Distance)用于描述两点之间的距离, 以二维空间为例, 两点之间的曼哈顿距离就是两点之间最短的距离, 计算相对简单且速度很快,A点和B点之间的曼哈顿距离定义如下

dMD(A,B)=|xA-xB|+|yA-yB|

(13)

其中(xA,yA),(xB,yB)为A点和B点的坐标。

设有两个概率分布X,Y的方差表示为

D(X)=E(X2)-[E(X)]2

(14)

D(Y)=E(Y2)-[E(Y)]2

(15)

两个方差之间的dMD距离为

dMD(D(X),D(Y))=|D(X)-D(Y)|

(16)

通过计算各模态分量与原信号之间的曼哈顿距离评价模态与信号之间的相似程度, 并用于区分信号分量和噪声分量。MD作为衡量模态与原始信号的相似程度, 把MD增量最大的两个相邻的IMF作为信号分量和噪声分量的转折点。

2 SG-VMD-SVD去噪算法

基于SG-VMD-VMD去噪算法流程图如图1所示。

图1 去噪方法流程图Fig.1 Flow chart of denoising method

基于上述分析, 笔者提出了Savitzky-Gloay平滑滤波、 VMD和频域SVD结合的去噪方法(SG-VMD-频域SVD去噪法), 实现步骤如下。

步骤1) 对原始信号进行SG平滑滤波, 将拟合低频部分, 滤除部分高频噪声, 提高信号的信噪比。

步骤2) 将滤波后的信号进行VMD分解, 对得到的IMF分量与原始信号进行相似程度分析, 计算各IMF分量与原始信号之间的曼哈顿距离。

步骤3) 比较两个相邻IMF与原始信号的曼哈顿距离, 选取MD增量最大的两个相邻IMF分量作为信号分量与噪声分量的转折点。

步骤4) 对噪声分量进行傅里叶变换, 作奇异值分解, 选取合适的奇异值阶数, 进行重构得到降噪后的频域序列, 最后做傅里叶逆变换, 得到降噪后的时域序列, 即为降噪后的信号。

步骤5) 将信号分量和降噪后的分量进行重构, 得到最终降噪信号。

3 仿真分析

3.1 仿真信号

为验证笔者提出算法的有效性, 利用3个不同频率的纯谐波信号组成一个三次谐波复合信号, 再加入高斯白噪声作为仿真信号, 使其符合实际采集的管道泄漏信号特征。复合信号各分量信号的中心频率分别为4 Hz,24 Hz,288 Hz, 即仿真信号

f(t)=cos(8πt)+0.5cos(48πt)+0.05cos(576πt)+η

(17)

其中η为高斯白噪声, 噪声强度为0.1 dBW。采样频率为1 000 Hz, 采样点数为1 000, 合成仿真信号如图2所示, 从频谱图中可以明显看到前两个频率成分, 第3个频率成分完全被淹没在噪声中。

将原始含噪信号采用笔者去噪方法进行降噪, 将含噪信号输入到SG平滑滤波中, 滤波后的信号如图3所示。从图3中可以明显看出, 信号被滤除部分噪声, 从频谱图中能看到仍有部分噪声干扰, 使用信噪比评价降噪效果的好坏, 此时信噪比从原来的0.1 dB提升到3.1 dB。

图2 仿真信号f(t) 图3 SG滤波后信号Fig.2 Simulation signal f(t) Fig.3 SG filtered signal

将经过SG滤波后的信号进行VMD分解, 在对仿真信号进行VMD处理时, 由于仿真信号由3个不同频率成分的余弦信号和白噪声组成, 故预设K=4, 设定α将为默认值2 000, 仿真信号分解为4个模态分量, 4个模态分量如图4所示。

图4 VMD分解后的模态分量Fig.4 Mode components after VMD decomposition

分别计算出4个模态分量与原始信号的方差值, 根据式(15)计算出各IMF与原始信号的方差之间的曼哈顿距离, 如图5所示, IMF1、 IMF2之间的MD增量急剧增加, 由此选取IMF1、 IMF2作为信号分量和噪声分量的转折点, 因此根据结果选取IMF1作为信号分量, 剩余分量作为噪声分量。

将剩余的噪声分量进行重构, 做频域奇异值分解, 选取合适的奇异值, 将其余噪声贡献的奇异值置为0, 重构后经傅里叶逆变换得到的时域降噪信号。

最后, 将信息分量和频域SVD去噪后的分量进行重构, 得到最终降噪的信号。降噪后的信号如图6所示, 由图2和图6进行对比可知, 降噪后能较好地还原信号的基本特征, 且信噪比大大增加。

图5 各分量方差的曼哈顿距离 图6 SG-VMD-SVD去噪后的信号图Fig.5 The Manhattan distance of the Fig.6 Signal diagram of SG-VMD-SVD variance of each component fter denoising

3.2 实验对比

为验证笔者提出方法的有效性以及优越性, 分别使用基于SG-VMD与时域奇异值分解的降噪方法、 基于VMD与小波变换的降噪方法、 单一VMD降噪法与笔者提出的去噪方法对仿真信号进行处理。采用信噪比(SNR: Signal Noise Ratio)(单位为dB)、 均方误差(MSE: Mean Square Error)和拟合接近度(POF: Proximity of Fitting)。分别计算几种降噪方法降噪后信号的SNR、 MSE和POF,通过定量分析4种方法的降噪性能, 评价指标定义如下[16-17]

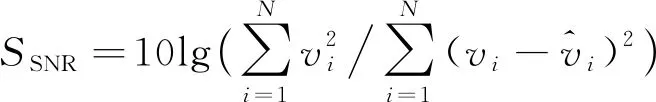
(18)

(19)

(20)

图7 各种降噪方法对比图Fig.7 Comparison diagram of various noise reduction methods

下面将从SNR、 MSE以及POF 3个指标评价降噪效果, 具体如表1所示。

表1 仿真信号不同方法降噪后评价指标Tab.1 Evaluation indexes after noise reduction by different simulation signal methods

对比4种方法可知, SNR越大, 说明去降噪方法的性能越好; 相反, MSE越小, 则降噪方法性能越好, 而POF越大, 则表示降噪后的信号与原始仿真信号相似程度越大, 更大限度地还原了信号。由表1可见, 对仿真信号采用笔者方法处理所得的SNR最大、 MSE最小且POF最大, 说明笔者提出的改进方法能更好提高SNR,降低MSE, 还原原始信号的特征以及形状。因此, 该仿真信号实验验证了笔者方法的有效性与优越性。

4 管道泄漏信号检测与分析

笔者从东北石油大学管道泄漏检测实验室采集数据。实验室仿真管道总长为160 m, 管径为DN 50 mm(公称直径), 管壁厚为4 mm, 管道内可实现气体和液体的运输。采用压缩空气仿真气体管道, 其中气体压力为0.5 MPa, 流速16 m/s, 泄漏口径16 mm。

实际管道运输过程中, 传感器采集的管道信号含有大量的噪声, 将采集的实际信号采用SG-VMD-频域SVD降噪法对实测数据进行去噪, 在进行VMD分解时, 通过EMD分解模态数预设VMD分解的模态数K值[18]。降噪前后的信号如图8所示。由图8可知, 原始采集信号中含有大量的噪声, 采用SG-VMD-频域SVD降噪法降噪后, 高频噪声部分被明显去除, 降噪后仍然保留原始信号的基本特征。分别采用SG-VMD-频域SVD降噪法、 单一VMD法、 VMD-小波变换法、 SG-VMD-时域SVD法对实测信号进行去噪, 计算出降噪后的信噪比、 均方误差、 拟合接近度(见表2)。由表2可知, SG-VMD-频域SVD降噪法降噪后的信号SNR最大, MSE最小, POF最高, 证明笔者方法对实际的管道泄漏信号有较好的降噪效果, 降噪后的性能指标相对较好。

图8 降噪前后实际管道泄漏信号Fig.8 Actual pipeline leakage signal before and after noise reduction

表2 实际管道信号不同方法去噪后评价指标

5 结 语

为提高泄漏信号的去噪效果, 笔者提出了一种SG-VMD-SVD的去噪方法。通过SG平滑滤波预处理信号, 滤除部分高频噪声, 提高信噪比； 然后进行VMD分解, 根据曼哈顿距离选取信号分量和噪声分量, 将噪声分量进行频域SVD去噪； 最后将有效模态分量和去除噪声后的剩余模态分量进行重构, 可以减少高频段有用信息的丢失, 并能较大程度地去除信号在管道传播中混入的噪声。通过仿真信号和实验室管道采集信号进行试验, 与其他算法相比, 通过去噪性能指标证明了笔者提出的算法在信号去噪方面有着较好的优越性, 并且在管道泄漏检测方面有着较好的前景。