基于Shapelets的多变量D-S证据加权集成分类
宋奎勇, 王念滨, 王红滨
(1. 哈尔滨工程大学 计算机科学与技术学院, 哈尔滨 150000; 2. 呼伦贝尔职业技术学院 信息工程系, 内蒙古 呼伦贝尔 021000)
0 引 言
多变量时间序列在工业、 医疗、 金融诸多领域广泛存在, 如医疗中检测病人心跳、 血压、 脉搏数据; 机械振动中不同位置传感器检测齿轮故障数据。一些与时间相关的数据如基因、图像也可通过数据变换成为时间序列。通常, 相较于单变量时间序列, 分类多变量时间序列会更复杂[1]。
在当前研究中, 多变量时间序列分类包括基于距离的、 基于特征的和基于集成学习的方法[1]。基于距离的方法考虑到同类之间距离较近而不同类之间距离较远, 常用的距离度量有欧氏距离、 马氏距离[2]、 动态时间弯曲(DTW: Dynamic Time Warping)距离[3]。DTW方法不但在单变量分类中有很好的效果, 在多变量分类中也有不错的表现[4]。Shapelets[5-8]和深度学习[9-11]是当前基于特征多变量分类主流方法。Shapelets是通过学习得到的时间序列子序列, 此方法可解释强、 准确度较高, 但是, 生成Shapelets的时间复杂度较高。近年来, 深度学习方法如卷积神经网络(CNN: Convolutional Neural Network)[12]、 循环神经网络(RNN: Recurrent Neural Network)[10]及长短期记忆网络(LSTM: Long Short Term Memory)[11]在多变量分类中得到关注, 这些方法通过构建深度模型提取深度特征融合分类, 分类准确度较高, 但是, 与其他深度学习方法一样可解释性不强。基于集成学习方法[13-14]可以融合不同分类方法的优点, 取长补短, 能取得较高的分类结果, 然而选择适合的集成方法是一个挑战。
集成学习通过组合多个基分类器为一个强分类器, 可以获得比单一基分类器优越的泛化性能。集成学习方法可分成两大类: 一类是基分类器间存在强依赖关系, 必须串行生成的序列化方法, 如Boosting[15]; 另一类是基分类器间不存在依赖关系, 可同时生成的并行化方法, 如Bagging[16]和Random Forest[17]。笔者提出基于Shapelets的多变量D-S证据加权集成分类方法。首先, 使用Shapelets作为基分类器, 基分类器间不存在依赖关系, 且单个Shapelets分类准确度较高, 能得到“好而不同”的基分类器, 类似于Bagging方法策略; 其次, 使用D-S证据加权集成基分类器。不同基分类器性能不同, 使用基分类器分类准确率对基分类器加权, 基分类器分类准确率越高, 则在集成时所占权重越大, 如此集成分类器必然越准确。D-S证据理论集成能给出合理的结果, 并且为了减少证据冲突, 对证据施加限制侧率。最后, 与经典DTW及最新的深度学习、 集成学习方法进行了比对, 取得了较好的结果。
1 背景知识
1.1 Shapelets
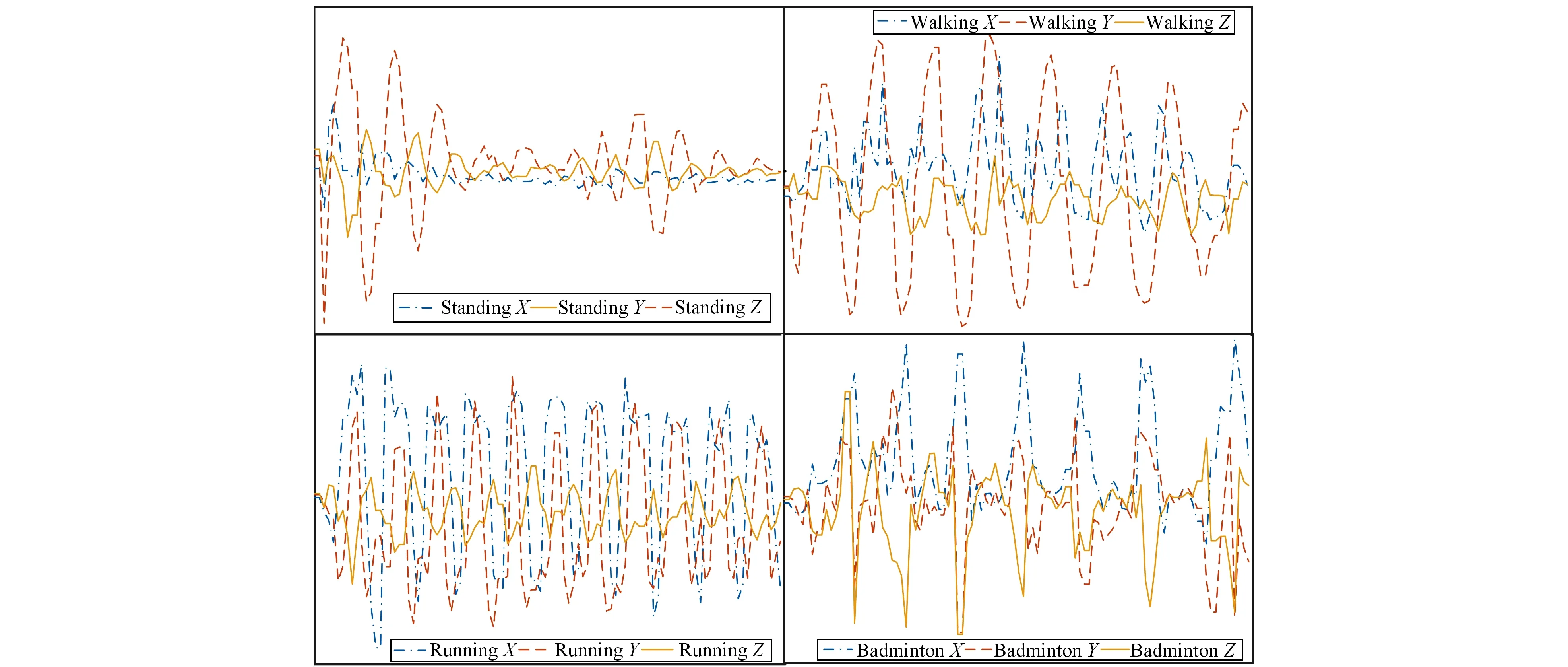
单变量时间序列T={t1,t2,…,tn},T的长度为n,T对应类标签为c,c∈C。若T两个等长为l时间子序列s、r, 且l (1) 定义1 给定长度为l的序列s及长度为n的序列T, 且l (2) 定义2 一个Shapelets定义为f=(s,l,δ,c),s是长度为l的子序列,δ是分裂阈值,c是类标签, 这里有 ∀(T,c)∈D⟹ddist(s,T)≤δ (3) 在图1中T为单变量时间序列,S为Shapelets, 最佳匹配位置为30, Shapelets的长度为20。 图1 时间序列Shapelets示例Fig.1 Time series shapelets Example D-S证据理论[18]是经典概率论的推广, 能满足比贝叶斯理论更弱的条件, 具有直接表达“不确定”和“不知道”的能力。D-S证据理论用辨识框架Θ表示样本空间, 它是一个有限集合, 集合中元素互不相容且构成完备性。Θ的幂集表示为2Θ, 幂集是Θ所有子集的集合。 定义4 设函数fBel: 2Θ→[0,1], 且满足 (4) 则fBel称为A的信任函数, 它表示证据对A为信任程度。 定义5 设函数pl: 2Θ→[0,1], 且满足 pl(A)=1-fBel(A), ∀A⊆Θ (5) pl称为似然函数, 它表示对A为非假的信任程度, 而fBel(A)是对A为假的信任程度, 即对A的怀疑程度, 如图2所示。 图2 信息的不确定性Fig.2 Uncertainty of information 由于fBel(A)表示对A为真的信任程度, PI(A)表示对A为非假的信任程度, 而且PI(A)≥fBel(A), 称fBel(A)和PI(A)分别为对A信任度的下限和上限, 记为[PI(A),fBel(A)], 其表示了对A的不确定区间。 定义6 设m为基本概率赋值函数, 如果m(A)>0, 则称A为Bel的焦元; 信任函数fBel的所有焦元联合称为核。 (6) 设fBel1,fBel2,…,fBeln是同一识别框架Θ上信任函数,m1,m2,…,mn是其对应的基本概率分配函数, 若m为m1,m2,…,mn的合成概率分配函数, 则有 (7) 若m变量时序数据集T由Ti组成,Ti=[T1,T2,…,Tm],i∈[1,k], 其中Tj为第j个维数为n的单变量数据。为在单变量上学习基分类器, 首先把多变量数据重新划分为m组单变量数据,m变量数据集T共k个, 从每个多变量Ti中抽出单变量数据, 重新组成一个单变量数据集。 如抽出T1组成新的单变量数据集T11,T12,…,T1k。这样, 就把一个多变量数据集划分成m个单变量数据集, 然后, 可以在训练集上学习Shapelets并计算器分类准确率。 Shapelets[5]是一组时间序列的子序列, 在本文中, 把Shapelets作为一个基分类器, 则m变量时间序列数据对应m个基分类器。为了在单变量上学习Shapelets并确定最优阈值, 引入文献[5]中基于最大熵方法确定最优分裂阈值, 熵计算公式如下 (8) 其中mc是c类数据的数量,M是所有时间序列的数量。为了获得基分类器Shapelets, 计算所有候选Shapelets最优分裂阈值, 并把数据集分成DL和DR两部分。若数据集DL和DR的熵为EL和ER, 则 (9) 在所有候选Shapelets中, 得到最大的IIG为Shapelets, 也就是基分类器。如图3所示, 对二分类数据进行分类, 在数轴上实圆为一类, 方块为一类, 中间带箭头的竖线位置为最优分裂点, 在二分类中最优分裂点把数轴分成两部分。 图3 最优分裂阈值Fig.3 Optimal split threshold 从图3可知, 最优分裂点实圆点一边出现了方块, 在右侧方块一边出现了实圆点, 这表示为错误的分类。则Shapelets分类准确率可计算为 (10) 其中fz为正确的分类数量,ftotal为分类数据总数。图3给出的是二分类问题, 若是n分类, 则会选出n-1个Shapelets及对应的阈值, 现以三分类为例展示多类分类策略。如图4所示, Ⅰ和Ⅱ是一组Shapelets, Ⅰ和Ⅱ的Shapelets和阈值在图4上部。Ⅰ按照阈值σ1把数据集分成两部分, 距离小于σ1的被分在A类, 距离大于σ1的被Ⅱ继续划分, 距离小于σ2的划到B类, 距离大于σ2的划到C类。若多于三分类问题, 则与三分类相似。 图4 Shapelets多分类划分策略Fig.4 Shapelets multi-classification partion strategy 多分类准确率计算方法与二分类类似, 模型分类准确率等于正确分类数量除以总数量。基分类器分类准确率反映基分类器的优劣, 在多变量m个基分类器中, 准确率越高的基分类器在强分类器中所占权重越大。 在集成学习中, 要得到泛化性能强的集成, 集成学习中的个体分类器应尽可能相互独立, 在本文中, Shapelets对应一个单变量的子序列, 多变量Shapelets相互之间独立, 这为集成学习提供了条件。笔者提出使用D-S证据理论组合基本概率指派BPA(Basic Probability Assignment), 并在计算BPA时对基分类器加权, 最后在Dempster组合中提出解决证据冲突的策略。 2.2.1 BPA的生成方法 基本概率指派BPA是证据理论在实际应用中的关键问题, BPA直接影响到D-S证据组合的结果[19-21]。笔者依据Shapelets决策树结构, 提出一种加权BPA生成方法, 如图5所示。 在图5中, 有3个从训练集中学习到的Shapelets基分类器, 权重分别是70%、 90%、 50%。现有一测试数据, 已知此数据类别为A。经3个分类器分类后, 其BPA如图5a所示。经D-S合成预测结果为B, 如图5b所示。分析预测错误原因, 由于分类器3对B预测较高, 直接影响了预测的结果, 而分类器3的准确率只有50%。由此笔者给分类器加权, 权重就是分类器的分类准确率。经过加权后, BPA如图5c所示。加权后降低了分类器3对结果的影响, 经计算得到分类结果为A。 若分类器权重为g, 加权前bBPA为bBPAb, 则加权后的概率指派bBPAa为 bBPAa=g*bBPAb (11) 2.2.2 证据组合冲突解决方法 在D-S证据理论中, 存在证据冲突的问题[22], 融合高度冲突的证据会导致两个结果: 一个是产生不合理与直觉相悖的结果, 如Zadeh悖论[23]; 二是融合后的结果合理, 但不利于决策。为得到较好的融合结果, 笔者设定两个规则: 1) 选取部分分类准确率高的基分类器进行Dempster组合, 如分类准确率低于50%的基分类器舍弃; 2) 基分类器Shapelets在BPA生成时, 若类别较多, 则舍弃部分权重较小的BPA, 用不确定θ代替, 从而提高计算效率, 同时也符合D-S证据理论的基本思想。 以图6为例, 若此数据集为4变量。基分类器的准确率分别为80%,90%,70%,40%, 经过规则1)筛选, 舍弃第4个基分类器。前3个基本概率指派函数为 m1=(A,B,C,D,E)=(0.640,0.180,0.090,0.045,0.045) m2=(A,B,C,D,E)=(0.810,0.095, 0.048,0.024,0.024) m3=(A,B,C,D,E)=(0.490,0.255,0.127,0.064,0.064) 设定权重低于0.1的类别被合并成θ, 经过规则2)过滤后,θ取代了D,E m1=(A,B,C,θ)=(0.640,0.180,0.090,0.090) m2=(A,B,C,θ)=(0.810,0.095,0.048,0.048) m3=(A,B,C,θ)=(0.490,0.255,0.127,0.127) 使用Dempster组合规则式(7)计算得到 m=m1⊕m2⊕m3=(0.97,0.015,0.007 5,0.007 5) m(A)=0.97, 最后数据预测为A, 得到正确结果。多个基分类器的组合具有如下优点[12]: 1) 能提高泛化能力; 2) 可降低陷入局部极小点的风险; 3) 扩大假设空间, 得到更好的结果。 在笔者算法中, 由于使用了基于信息增益的Shapelets生成方法, 使用brute-force算法判断大量的子序列时间复杂度为O(n2m4), 其中n为训练集中时序数据数量,m是一条时序数据的长度。基于最小距离的提前终止策略和基于信息增益的熵剪枝策略被使用[5]。与生成Shapelets的时间复杂度相比, 计算Shapelets分类准确率及BPA的生成及Dempster组合的时间在O(n)的时间内即可完成, 所以这部分时间可忽略不计。 笔者使用JAVA语言在开源Weka框架内实现了算法。遵循文献[8]中实验方法, 对数据进行100倍重采样, 对每种算法进行了多次试验, 试验结果取多次试验平均值, 并与其他算法的结果进行比对。 从UEA-UCR[24]中选取部分多变量时间序列数据, 如表1所示, 共21个等长序列, 包括序列名称、 训练集数量、 测试集数量、 每个多变量包含单变量的序列数量、 序列的长度以及类别数量。这些数据集以ARFF格式存储, 并在Weka[25]中打开。 表1 实验数据集Tab.1 Experimental dataset 人类活动识别是基于加速度计数据或陀螺仪数据预测类别的问题, 数据是三维或六维坐标。BasicMotion是HAR中的一个, 该数据是学生戴着智能手表进行4类运动收集的3D加速度计和3D陀螺仪数据, 4类活动分别是站立、 行走、 跑步和打羽毛球。 要求参与者记录运动共5次, 并以10 Hz的频率采样数据10 s。笔者选取了BasicMotion一个实例进行了展示, 共4类运动, 每类包括三维数据X,Y,Z, 例如WalkingX,WalkingY,WalkingZ,加速度计数据如图6所示。陀螺仪数据如图7所示。 图6 BasicMotion加速度计数据序列图Fig.6 Sequence diagram of BasicMotion accelerometer data 图7 BasicMotion陀螺仪数据序列图Fig.7 Sequence diagram of BasicMotion cyro data 笔者选取了5种不同类型方法进行对比, 包括DTW、 gRSF(generalized Random Shapelet Forest)、 MLCN(Multivariate LSTM-FCNs)、 MUSE(Multivariate Unsupervised Symbols and dErivatives)和HIVE-COTE(Hierarchical Vote Collective of Transformation-based Ensembles)。DTW应用到多变量中演化出两种方法: DTWD是多变量依赖方法; DTWI是多变量独立方法。若给定二维多变量序列Q和C, 则DTWD(Q,C)=DTW(QX,QY,CX,CY), DTWI(Q,C)=DTW(QX,CX)+DTW(QY,CY)。gRFS[26]是基于Shapelets广义随机森林算法, 该算法生成一组基于Shapelets的决策树, 其中用于构建树的实例的选择和Shapelet的选择都是随机的。MLCN[11]是基于LSTM神经网络方法, 该方法把注意力模型引入到多变量分类中。MUSE[13]是一种无监督符号表示与演化方法, 它首先使用滑动窗口方法构建多元特征向量, 然后按窗口和维度提取离散特征, 通过特征选择去除非歧视性特征, 并由机器学习分类器进行分析。HIVE_COTE[14]使用概率投票分层结构集成5个基分类器, 从而显著改善了集成结果。这5种不同类型的算法代表多变量分类最新的研究成果, 在不同的数据集上取得了较高的结果。为了验证笔者算法, 与这5种算法在21个数据集上对比实验, 实验结果如表2所示。 从表2中数据对比可以看出, 笔者算法在11个数据集上取得优势, 其中在BasicMotions和Epilepsy上与其他几个算法都取得了100%的正确率。HIVE_COTE在FaceDetection和EthanolConcentration上取得领先, 并且整体表现优异, 在大部分数据集上排在前列。DTWD算法好于DTWI, 并且在Handwriting和PenDigits上取得领先。MLCN整体表现一般, 深度学习方法有待进一步提高。MUSE方法在3个数据集上取得领先, 整体表现好于其他算法。 表2 不同方法试验对比Tab.2 Test comparison of different methods 对分类问题, 分类准确率是很好的衡量不同算法优劣的标准, 但有的算法在一些数据集上表现好, 在另一些数据集上表现不好。为了进一步对比算法在所有数据集上的优劣, 采用机器学习领域广泛使用Friedman测试作为评价算法性能的标准, Friedman测试把所有算法在每个数据集上的分类准确率进行标记排名, 如排名“1”,“2”一直到N, 这样M个算法在N个数据集上的排名组成N×M矩阵。然后计算每个算法的平均标记值 (12) 其中hij表示第i个算法在第j个数据集的标记值。当M和N足够大时(M>5,N>10), 使用Friedman统计量 (13) 可以使用具有M-1个自由度的卡方分布近似。这样不同算法的性能差异可以通过包含平均次序和无明显差异算法组的关键差异图[27](Critical Difference Diagram)表示。在21个数据集上采用100倍重采样关键差异图, 结果如图8所示。 图8中粗横线表示这几个算法属于同一集团, 集团内算法效率差异不大。这些横线是通过Wilcoxon有符号秩检验和Holm校正测试得到。可以看出, 笔者算法、 MUSE和HIVE-COTE属于第1集团, 第2集团包括HIVE-COTE、 gRSF和MFCN, 第3集团包括gRSF、 MFCN、 DTWD和DTWI。 从表2和图8中可以得到如下结果: 经典的DTW算法在个别数据集上表现不错, 但整体上不如最新的几个算法; 深度学习算法MFCN并没有表现出优势, 虽然它在图像识别等方面表现优异; MUSE和HIVE-COTE整体表现优秀, 但是, MUSE会带来巨大的内存开销, 并且随着问题规模的增加而急剧增加。在本次试验的21个数据集上, 其内存使用为26 GByte[4]。而HIVE-COTE在分类准确率上不如MUSE; 笔者算法在准确率上取得一定的优势, 并且由于使用了减少冲突策略, 使集成花销不大, 整体上资源花销适中。 图8 关键差异图Fig.8 Differentiated graph analysis 当前, 多源传感器用于检测、 控制等方面, 这些传感器产生大量多变量时间序列数据。充分利用这些数据有着巨大价值。笔者提出一种基于Shapelets的多变量D-S证据加权集成分类方法。对基分类器Shapelets加权, 增加分类准确率高的基分类器权重, 减少分类准确率低的基分类器权重, 得到了更准确的结果。近年来, 深度学习、 集成学习在多变量分类中得到更多的关注, 在以后的工作中, 把深度学习和集成学习应用于多变量分类、 多源数据融合中。


1.2 D-S证据理论



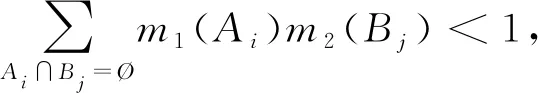

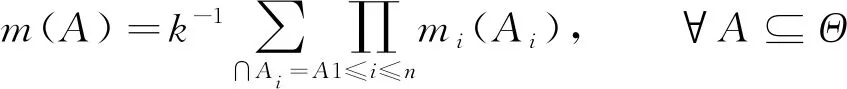

2 基于Shapelets多变量D-S理论加权集成分类
2.1 学习Shapelets并计算权重
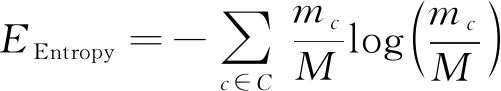
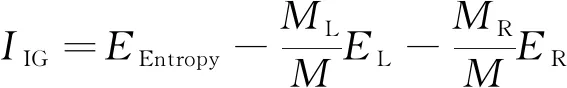

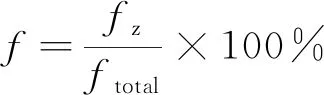

2.2 D-S证据理论加权组合策略
2.3 时间复杂度分析
3 实验验证与结果分析
3.1 实验数据集

3.2 比对方法及分类准确率对比

3.3 关键差异对比
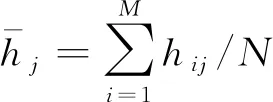


4 结 语

