基于优先级经验回放的SAC强化学习算法

刘庆强, 刘鹏云

(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)

0 引 言

相对于有监督学习需要人工标注数据集标签进行学习, 强化学习算法通过自行与环境(Environment)交互, 尝试最大化从环境中得到的奖励(Reward)获得最优的策略。在DQN(Deep Q-Learning)算法[1]之后, 强化学习与深度神经网络相结合, 使强化学习算法能处理更复杂, 维度更高的问题, 其表现效果得到了迅速提升, 并在围棋[2-3]、 游戏[4-5]、 投资交易[6-8]、 推荐系统[9-10]以及导航规划[11-12]上得到了广泛应用。

强化学习算法[13]总体可被分为三大类： Actor方法, Critic方法和Actor-Critic方法。Actor方法直接尝试学习出最优决策过程； Critic方法通过评估当前状态采取不同动作可得到的累计回报期望, 选择期望最大的动作间接学习最优策略； Actor-Critic是两种算法的结合, 算法的Critic部分学习以更好的误差拟合值函数, Actor与环境交互并根据Critic的反馈迭代自身参数, 尝试学习出最优策略。

近期, 深度强化学习领域获得了显著的研究进展, OpenAI提出基于隐式课程学习模式[14]的强化学习算法, 使智能体可以不断找到新任务, 学习新策略。Mendonca等[15]提出基于监督学习的元强化学习算法, 能有效帮助探索, 利于在稀疏奖励环境中有效学习。Efroni等[16]提出基于有限时域前瞻策略(Finite-Horizon Lookahead Policies)的强化学习算法, 利用最佳树路径返回值备份根节点后代值, 取得了良好的效果。Ciosek等[17]提出OAC(Optimistic Actor Critic)算法, 使用两个置信区间估计value值, 高的指导探索, 低的防止过拟合。Haarnoja等[18]提出SAC(Soft Actor Critic)算法, 通过引入最大熵增强了Actor Critic算法的探索能力和稳定性, 并在随后的升级算法[19]中加入了熵权重的自动调整, 在训练前期熵部分的权重较大, 引导Agent更主动探索环境, 并在后期逐渐衰减熵的权重, 让Agent收敛更加稳定。

针对SAC算法中经验池所有样本都以等概率随机采样, 忽略不同样本具有不同重要性的信息, 造成训练速度慢, 训练过程不稳定的缺点, 笔者提出基于优先级经验采样的SAC算法(PER-SAC： Prioritized Experience Replay Soft Actor Critic), 通过在训练过程中引入优先级经验采样机制, 同时根据Critic和Actor的误差计算TD(Temporal-Difference)误差, 使TD误差较大的样本有更大的概率被采样及训练, 并使网络优先训练估值误差较大和策略表现不好的样本。实验结果表明, 所提PER-SAC(Prioritized Experience Replay Soft Actor Critic)算法训练效率和稳定性相较于原始SAC算法有明显提升, 具有较好的性能。

1 强化学习, SAC算法及优先经验回放

1.1 强化学习

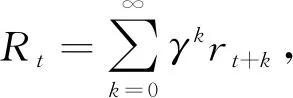
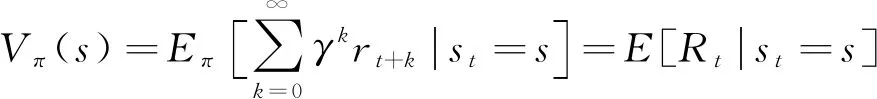
(1)

其动作值Qπ(s,a)=E[Rt|st=s,a], 则最优策略为始终选择当前状态下Q值最大的动作, 可表示为

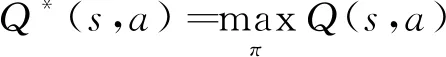
(2)

通过Bellman方程迭代动作值函数可表示为

Q*(st,at)=E[rt+γmaxQ*(st+1,at+1)]

(3)

在引入深度神经网络后, 强化学习算法中动作值函数Q和状态值函数V都可以使用多层神经网络近似, 深度神经网络理论上可以拟合任意复杂度的函数, 该特性使强化学习算法能被用于解决更加复杂的控制和决策问题。但神经网络具备的“黑盒”复杂特性, 也使深度强化学习算法面临训练效率低, 稳定性差, 对超参数敏感等问题。

1.2 SAC算法

SAC算法通过在原有的直接最大化奖励期望的基础上, 引入了最大熵, 此时算法的目标变成同时最大化奖励期望和熵, 可表示如下

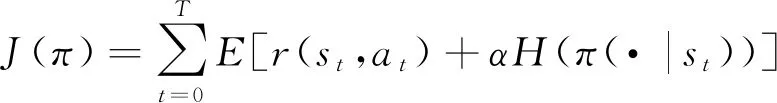
(4)

其中H是策略π在状态st时的动作的熵,α是权重系数。通过引入熵鼓励策略探索更多动作, 与PPO(Proximal Policy Optimization)[20], A3C(Asynchronous Advantage Actor-Critic)[21]等算法将动作熵作为正则项不同, SAC直接将最大化熵内置于目标函数中。SAC算法分为2部分： 策略评估和策略提升。

策略评估。SAC算法定义SoftQ值如下

Qsoft(st,at)=r(st,at)+γE[Vsoft(st+1)]

(5)

Soft版本状态值函数V定义如下

Vsoft(st)=E[Q(st,at)]-logπ(at|st)

(6)

策略提升。使用KL散度(Kullback-Leibler Divergence)优化策略

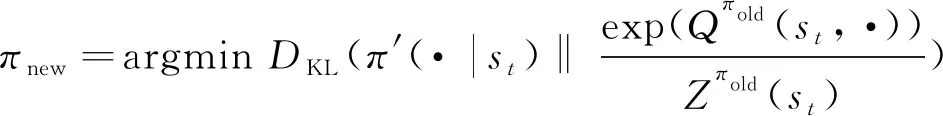
(7)

其中Zπold(st)是归一化分布配分函数。策略πφ的输出是一个概率分布, SAC算法中使用了重参数技巧(Reparameterization Trick), 将策略πφ重新定义为

at=fφ(εt;st)

(8)

其中εt是重参数技巧中随机变量。根据上述定义, 训练过程中, Soft Q函数的更新梯度为

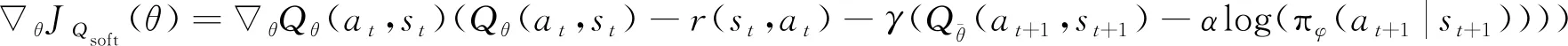
(9)

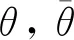
φJπ(φ)=φlogπφ(at,st)+(atlogπφ(at,st)-atQ(at,st))φfφ(εt;st)

(10)

SAC算法还支持自动调整熵的温度系数α, 算法初始温度系数较大, 鼓励智能体进行探索, 随着智能体慢慢收敛, 温度系数能自适应衰减。

1.3 优先经验回放

SAC算法训练时, 随机从经验池(Replay Buffer)中抽取一批样本训练, 不同样本间被选中的概率相等。优先经验回放通过赋予更重要的样本较大的权重, 训练采样时权重较大的样本能以更大的概率被抽取到, 因此, 如何确定样本的权重是关键问题。强化学习算法通过TD误差衡量算法修正幅度, TD误差的绝对值越大, 说明该样本对网络的校正效果越大。另外, TD误差较大的样本, 可能是该状态出现的次数较少, 智能体对该状态不熟悉故而表现不佳, 提高此类样本的出现概率能提高样本利用率, 加快智能体的学习速度。在优先级经验回放DQN[22]算法中, TD误差δj定义为

δj=r(st,at)+λQ′(st+1,at+1)-Q(st,at)

(11)

其中Q,Q′分别是Q网络和targetQ网络。样本j的采样概率

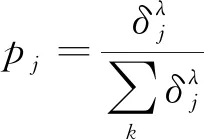
(12)

其中参数λ是优先级控制系数,δj是样本j的权重系数。使用概率采样机制能保证TD误差较小的样本仍然可以被采样, 保证了算法训练时样本的多样性。优先级回放改变了样本的采样频率, 因此需要引入重要性采样更新样本计算梯度时的误差权重

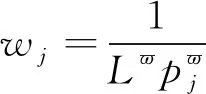
(13)

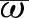
2 基于优先经验回放的SAC算法

PER-SAC算法通过将优先经验回放机制引入SAC算法提高算法的训练速度和稳定性。算法在训练时, 不再以等概率随机从经验池中抽取数据, 而是给重要的样本更大的权重, 增大其被采样概率, 同时随着训练的进行, 动态调整不同样本的权重, PER-SAC算法定义样本权重为样本训练时的TD误差。

2.1 综合全网络误差

值得注意的是, 在优先级经验回放DQN算法中只有一个Q网络, 其TD误差的计算方式也仅为单个Q网络的误差统计。而SAC算法为了减少值函数的估计偏差, 提高训练稳定性, 使用了两个Q网络, 训练时使用较小的Q值用于梯度计算, 加上策略π网络, SAC算法一共有3个网络, 分别为Q1,Q2,π网络。PER-SAC算法中的TD误差因此需要同时考虑3个网络的误差, 一个简单的方式是将3个误差直接相加

δj=abs(Td(Q1))+abs(Td(Q2))+abs(Td(π))

(14)

2.2 带调整系数的综合TD误差

直接将3个网络各自的绝对误差相加得到一个总误差。但由于Q网络与策略π网络的输出意义有着本质区别：Q网络的输出是对当前状态采取动作后得到累计回报的期望, 该值因不同环境差异很大, 通常远大于1。而策略π网络的输出是当前环境Agent采取不同动作的概率, 概率值不超过1。直接将3个网络的误差绝对值相加将导致策略π网络的误差部分对总体误差评估的影响较小, 降低算法的性能。PER-SAC算法通过在策略π网络的误差部分引入调整参数β将其适当放大, 解决了这个问题, 引入调整参数β后的总TD误差计算方法为

δj=abs(Td(Q1))+abs(Td(Q2))+βabs(Td(π))

(15)

在PER-SAC算法中, 前期探索阶段时网络还未训练, 因此误差信息未知, 默认设置所有样本TD误差为1, 此时算法退化为原始SAC算法。当网络开始从经验池抽取样本训练时, 以TD误差值统计每个样本的被采样概率。当某个批次样本训练完成后, 将其最新的TD误差更新回经验池。随着训练进行, 整个经验池的样本的TD误差都将被替换为真实的TD误差, 能最大程度发挥算法性能。图1给出了PER-SAC算法的结构及训练流程图, 在探索阶段Policy与环境交互得到样本并存储至经验池, 并将TD误差设置为1。当经验池样本满足训练要求后算法即可开始训练； 以TD误差统计各样本的采样概率进行采样。Q1和Q2分别计算其TD误差并更新梯度； 为降低训练偏差, 使用较小的Q值计算策略网络的误差； 根据式(15)计算总的TD误差, 并更新经验池中对应样本的TD误差。

PER-SAC算法的结构如图1所示。PER-SAC算法首先使用Actor与环境交互, 并通过重参数引入随机噪声加大网络对新状态和动作的探索力度, 然后将样本存储至经验池中。在训练阶段, 算法从经验池中根据权重进行概率采样, 更新两个Critic网络的参数, 同时选取输出值较小的Q网络指导Policy网络更新。最终根据3个网络的误差重新计算TD误差, 并将其更新至经验池中对应的样本。

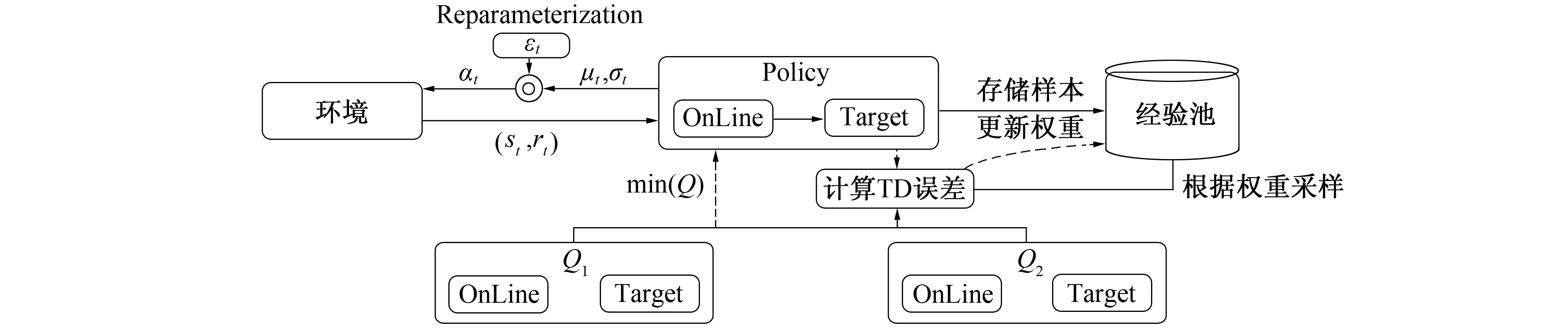
图1 PER-SAC算法网络结构图Fig.1 PER_SAC algorithm network structure diagram

PER-SAC算法步骤如下。

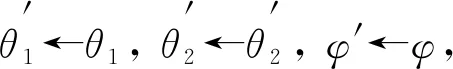
2) for each iteration do

3) for each environment step do

4) 根据状态st, 策略πφ采样得到动作at

5) 执行动作at, 获得立即奖励rt和下一状态st+1

6) 将经验样本(st,at,rt,st+1)存入经验池B中, 样本的TD误差初始化为1

7) 在经验池B, 根据样本的TD误差归一化作为概率pj进行样本采样用于训练

8) end for

9) for each gradient step do

10) 更新Critic网络参数

θi←θi-λθiJQ(θi) fori∈{1,2}

11) 更新Policy网络参数

φ←φ-λπφJπ(φ)

12) 更新温度系数α←α-λαJ(α)

13) 计算各个样本的TD误差, 更新到经验池B

14) 更新各个target网络参数

15) end For

16) end For

3 实 验

为验证PER-SAC算法对比SAC算法的优越性, 在2个不同的连续强化学习训练环境分别进行训练与测试, 并绘图观察两种算法在训练及测试中不同网络的误差更正情况。为了显示算法对优化算法的鲁棒性及对比其他强化学习算法的优越性, 在不同优化算法和环境中, 将PER-SAC算法与双延迟确定性策略算法(TD3: Twin Delayed Deep Deterministic policy), DDPG(Deep Deterministic Policy Gradient), SAC(Soft Actor Critic)算法进行了实验比较。实验证明PER-SAC算法在收敛速度, 训练稳定性, 智能体测试期间表现上均具有优异的表现。

3.1 实验环境

笔者分别选择强化学习Gym的钟摆环境(Pendulum-v0)和小车爬山环境(Mountain Car Continuous), 在不同的任务环境, 优化算法下分别将PER-SAC算法与SAC算法进行对比。实验使用的操作系统为Win10, 使用Python 3.7语言开发, Pytorch1.3-CPU版本搭建神经网络及训练。

钟摆环境(Pendulum-v0)是一个经典的强化学习训练和评估环境,图2给出了钟摆环境图。 该环境的目标是将钟摆保持垂直向上的姿态, 智能体需要通过观察钟摆的角速度、 正弦、 余弦值, 同时输出[-2, 2]间的连续值控制电机扭矩。

小车爬山环境也是一个连续空间的强化学习环境,图3给出了小车爬山环境图。该环境是一个一维的山坡, 目标是控制一辆动力不足的小车爬山坡, 小车自身动力无法直接完成该任务, 因此需要控制小车反复助跑蓄力冲上山坡, 在到达山顶前环境每一步的奖励反馈都是-1。该环境中智能体需要观察小车的位置和速度, 并输出[-1,1]间的连续值控制小车前进后退的力度。

图2 钟摆环境 图3 小车爬山环境Fig.2 Pendulum environment Fig.3 Mountain car environment

3.2 实验参数

为对比PER-SAC算法的改进效果, PER-SAC算法的参数与SAC算法完全一致, 实验部分环境将分别尝试钟摆环境和小车爬山环境； 优化算法分别尝试Adam和SGD。同时与TD3和DDPG算法进行了对比试验, 其他实验参数为SAC算法默认参数(见表1)。

表1 实验参数设置Tab.1 Experimental parameter setting

3.3 实验结果与分析

与有监督学习算法直接计算预测值与标签值衡量模型效果的方法不同, 强化学习以自身与环境不断探索试错逐步迭代出更优决策模型, 笔者将分别从Critic误差, Actor的误差及回合的累计奖励等角度评价算法性能。

图4给出了在钟摆环境下, 采用Adam优化算法, 批次大小设置为32时PER-SAC算法(绿色)与SAC(橙色)在训练及测试期间的表现情况。由图4a可以看出, 在整个训练过程中, PER-SAC的Q1网络的估计误差收敛比SAC算法更迅速, 更稳定。在训练至15 000次时PER-SAC算法的Q1误差已经接近1, 而SAC算法的Q1误差表现得更为震荡且紊乱, 在训练至15 000次时误差震荡上升至接近10。造成Q1和Q2网络训练误差先由小变大再由大变小的原因主要为网络随机初始化时神经元参数都比较小。随着训练参数逐渐增大, 其输出值也变大, 由于强化学习算法高方差和高偏差的特性, Critic的误差也在逐渐增大； 随着训练的继续, Critic对环境的评估越来越精准, 误差又逐渐下降, 值函数逐渐收敛。图4b中Q2网络的训练估计误差也表现出和Q1类似的特性, 这说明PER-SAC算法的两个值网络的训练效率和稳定性都得到了提高。图4c代表策略网络在训练期间的误差情况, 策略网络的误差描述的是策略网络与值网络分布的KL散度。在训练初期由于值网络和策略网络参数都比较小, KL散度的值也比较小。随着训练的进行, 值网络对状态的评估更加准确, 此时值网络与策略网络的KL散度会逐渐增大, 然而随着策略网络在不断根据KL散度的反馈迭代参数, 策略网络与值网络之间的KL散度接着又会逐渐减小, 在总体训练期间策略误差表现出先增大后减小。由图4c可观察出PER-SAC算法的策略误差收敛更加迅速, 加入优先经验回放使策略网络修正误差更加迅速, 同时由于PER-SAC算法的2个Q网络收敛比SAC算法更加快速稳定, 其对策略网络的梯度反馈在全局角度也更加精确, 能减少策略网络无意义的更新次数, 这使PER-SAC算法的策略的收敛效率相比于SAC算法有了较大提升。图4d和图4e分别代表了算法在训练期间的回合累计奖励, PER-SAC算法的表现优于SAC算法, 不仅增长更快速而且更加稳定。图4f表示熵的权重(温度系数)在训练期间的衰减情况, 总体两个算法都能使温度系数保持稳定的衰减, 利于策略的收敛, 引入优先经验回放并不会明显影响该过程。

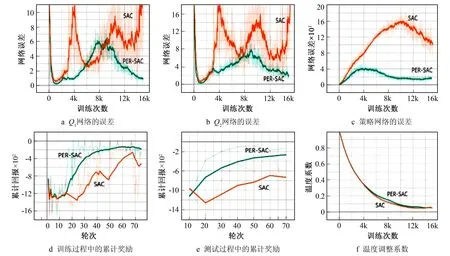
图4 PER-SAC与SAC在训练及测试期间误差收敛及奖励增长情况Fig.4 Error convergence and reward growth of PER-SAC and SAC during training and testing

表2给出了在两个环境, 不同的优化算法下, PER-SAC与其他3个比较算法在训练15 000步的测试表现, 采用的指标是指数平滑后的回合累计奖励, 采用指数平滑的方式能综合策略前面的回合的表现, 降低随机干扰。表格前两行是钟摆环境下的算法表现, 在Adam优化算法下, TD3,DDPG与SAC算法的表现较为接近, 在-700～-800范围内波动, 而PER-SAC算法表现明显优于前几个算法, 达到了-259.2。而在SGD优化算法中, SAC与PER-SAC算法较为接近, 而TD3与DDPG算法表现则差于Adam算法的结果。在小车爬山连续环境中, 无论在Adam还是SGD环境下, 4个算法均未能爬到山顶, 而选择了降低油耗的策略, 但通过其奖励仍然能反映出算法收敛的速度。TD3与DDPG算法在2种优化算法下的奖励均小于-2, 而SAC算法与PER-SAC算法均大于-1。在所有的试验中, SAC类算法表现都优于TD3和DDPG算法, 证明其最大熵策略的有效性。本次实验设置的步数为15 000, 相对普通强化学习实验的次数更低, 更能体现算法前期的收敛性能与学习速度, 而PER-SAC算法表现均优于SAC算法, 说明引入优先级回放机制能给SAC算法带来稳定的性能提升, 证明了PER-SAC算法的有效性。

表2 算法在不同环境及配置下训练最终回合平滑累计奖励(平滑系数为0.8)Tab.2 Cumulative reward of algorithm training in different environments and configurations (smoothing coefficientis 0.8)

4 结 语

笔者提出了PER-SAC算法, 通过将优先级经验回放机制引入SAC算法, 提升了算法的训练速度和稳定性, 并在不同环境, 不同优化算法等情况下与其他强化学习算法做了对比实验, 验证了所提算法的有效性。PER-SAC算法在衡量样本优先级时, 直接将3个网络的TD误差的绝对值相加, 样本重要性的评估方式较为简单, 引入的训练信息不够充分, 下一步的研究方向可以考虑引入更多环境奖励信息或训练信息帮助更好地评估样本优先级, 进一步优化算法训练性能。