想说·会说·善说：培养小学生数学说理能力的策略

（福州市台江第三中心小学，福建台江 350004）

“说理”指教师引导学生对知识点的本体、应用、生成脉络或是与其他知识点的联系等方面，进行深入细致的分析和阐述，从而透彻理解知识，深度把握知识内涵，让学生不仅知其然，更知其所以然。传统的小学数学课堂往往忽视“说理”，只求会算、会做，长此以往，将影响学生数学思维的发展。因此，在课堂上培养学生讲数学道理，是数学教学的重要任务之一。本文从“想说”“会说”“善说”三个方面，加强学生的说理训练，帮助学生深度学习，从而提高思维品质。

一、“想说”：创设学习情境，营造说理氛围

《义务教育数学课程标准（2011 年版）》指出，学生要“在生动具体情境中学习数学，在现实情境中体验和理解数学”。在课堂教学中，教师需要挖掘学生的生活经验，让学生在情境中感受真实的数学，营造说理的氛围。一切有效的教学都始于对学生已有经验的充分挖掘和利用。教师要从学生熟悉的生活情境中寻找能触发学生主动思考的问题。这样的问题才会成为学生感知思维的对象，在学生心里造成一种悬而未决但又必须解决的求知状态，学生才有想问、想说的欲望。［1］

例如，教学北师大版《分一分》一课时，三年级学生第一次接触“分数”这个较为抽象的概念。对于以形象思维为主的学生来说，学习这部分内容有一定的难度。教师创设学生生活中常见的“分东西”情境，边出示课件边提问，并要求学生伸出手指来回答。

师：4 个梨平均分给两个人，每人分到几个梨？（生伸出两根手指）

师：2 瓶橙汁平均分给两个人，每人分到几瓶橙汁？（生伸出1 根手指）

师：一个蛋糕平均分给两个人，每人分到多少？（部分学生伸出半个手指）

师：“一半”用手指个数表示显然不合适，还能用什么方式表示“一半”呢？

生1：我用文字“一半”来表示。

生2：我用“0.5”来表示。

生3：我用“二分之一”来表示。

师：说说你为什么用“二分之一”？［2］

这个案例从学生熟悉的情境入手，紧扣生活实际，将学生已有的整数平均分的知识和经验作为教学活动的起点。教师说，平均分4 个梨、2 瓶橙汁，学生们都非常迅速地伸出手指。这时，教师抛出“一个蛋糕平均分给两个人”的问题，学生不会回答，因为在他们的知识体系中只有整数的概念。思考后，学生纷纷举手表达观点，说明对于这个问题，学生是有生活经验的。教师再顺势让学生说说为什么这样表示，在生活化的情境中，深刻领悟学习分数的意义，切实掌握新知。教师以学习情境为桥梁，在整数和分数之间建立联系，唤起学生说理的欲望，使学生“想说”。

二、“会说”：掌握说理方法，明晰解题思路

朱光潜曾说：“话说得好就会如实地达意，使听者感到舒适发生美感，这样的说话就成了艺术。”在课堂教学中，教师要引导学生用准确的语言阐述观察和操作的过程，用精练语言讲清解题思路和算理，使学生学会使用数学语言讲数学道理，而且准确、简练、完整、有条理。教师必须加强对学生数学语言表达的规范训练，使学生掌握说理的方法，提高说理的能力。1.训练语言表达，奠定基础。及时纠正学生发言中存在的问题，学会用规范的语言、数学专用术语来说理。比如说长方体相对的两个面，必须用“完全相同”这个词。教师平时严格训练，学生就能学会清晰表达。2.训练读题能力，提供保证。首先，学会不添字漏字，读题要读得清楚、流畅。其次，学会圈出关键字或词，反复揣摩，经历寻疑、释疑、解析的过程。3.训练说理方法，创造条件。在教学中，采用多种方法让学生说理。比如看图说理，动手实践说过程，看算式说算理，解决问题讲思路。［3］

例如，教师出示题目与一幅购物图（见图1）。读完题思考后，让学生分组讨论。

文具盒25 元，书包比文具盒贵多了，书包可能是多少元?

师：这道题最关键的是要理解什么?

生：贵多了。

师：贵多了告诉我们什么信息?

生：我们这组同学认为，“贵多了”暗示书包比文具盒贵了至少有一倍。表格中的58 元比25 多了一倍以上，所以判断书包可能是58 元。

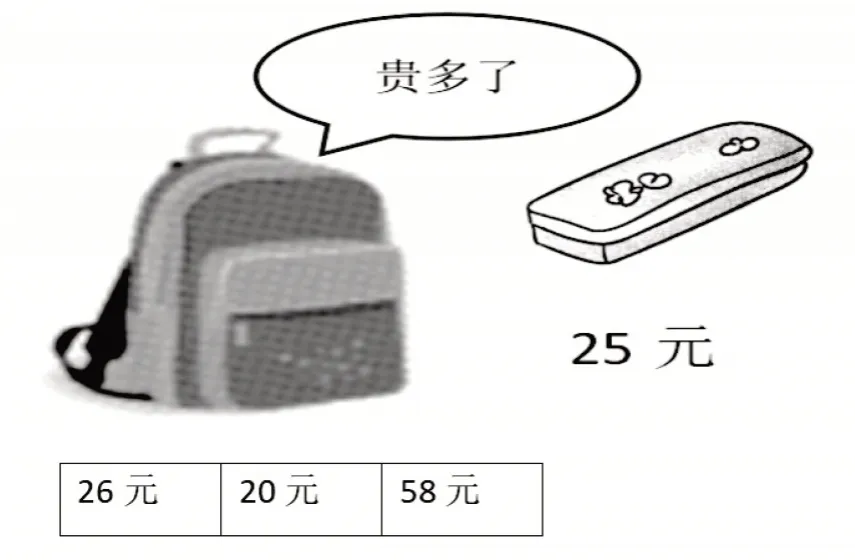
图1

这是一道图文结合题，对于低年级学生来说信息量较大，有图、有文字、有表格，还有一定的干扰信息。教师先让学生独立读题思考，然后在小组中讨论交流，相互补充信息，完整自己的信息链。再引导学生抓住关键信息“贵多了”，通过对“贵多了”的理解，淘汰前两个单价，最后选择“58 元”这一选项。教师训练学生读题提取信息，分析关键信息，进而判断推理，层层推进。掌握说理方法，明晰解题思路，使学生“会说”。

三、“善说”：组织问题辩论，推进深度学习

在课堂教学中，教师要有教学机智，要善于抓住生成，对问题适时开展课堂辩论。引导学生在问题驱动中深度思考，形成不同的结论时，让学生按不同的观点分组辩论，明析道理，解决问题。“真理愈辩愈明”，问题辨论说理有助于学生深度感知和理解知识，让语言表达和数学思维都得到锻炼和发展，从而达到深度学习的效果。

例如，教学《分数的大小比较》时，教师出示题目：“哥哥吃了一块月饼的，弟弟也吃了一块月饼的哥哥说他俩吃得一样多，对吗?”学生们各持己见。教师没有立即呈现答案，而是让意见不同的双方组队，展开辩论，说出自己的理由。

正方：他们吃得不一样多。

正方：他们的月饼可能大小不一样，如果一块大一些，另一块小一些，平均分成4 份，大块的就会比小块的大些，所以他们吃得不一样多。

反方：我们没有注意到单位“1”有可能不同。

案例中，教师在双方各持己见时捕捉到课堂生成，引导持相同意见的学生合作探究、商量对策，然后让持相反意见的学生展开辩论。最终双方达成共识：他们的月饼大小不一定相同，即单位“1”不一定是相同的，所以就不能说他们吃得一样多。学生们通过辩论，轻松突破理解单位“1”的难点。辩论说理不仅解决问题，而且让双方深刻理解数学问题背后的道理，增强了学生说理的严密性和逻辑性，提高说理能力，进一步推进深度学习，使学生“善说”。