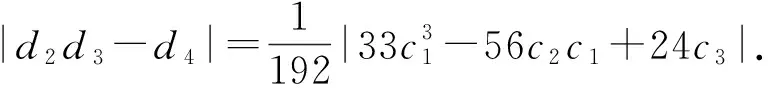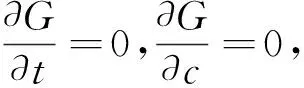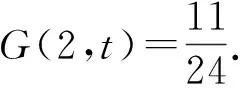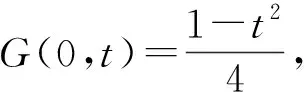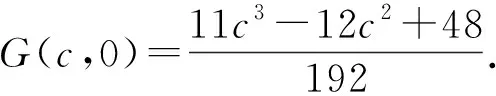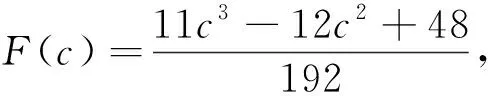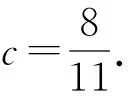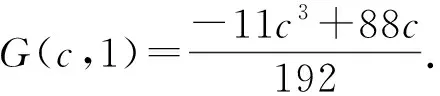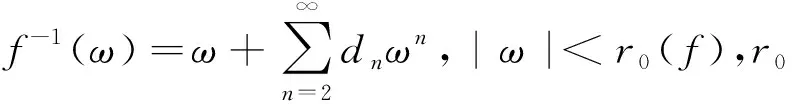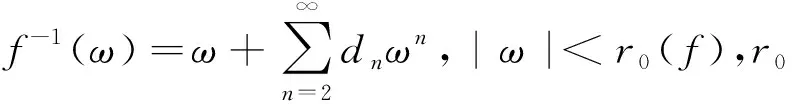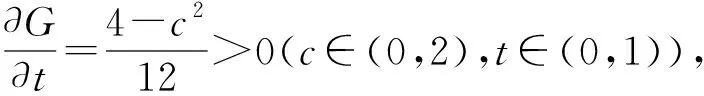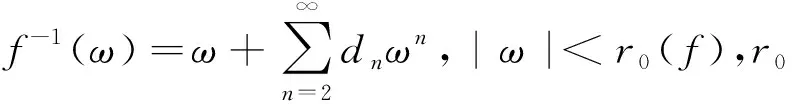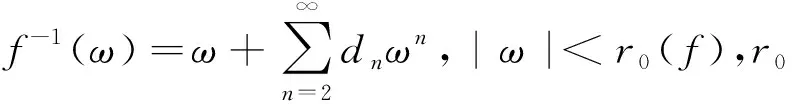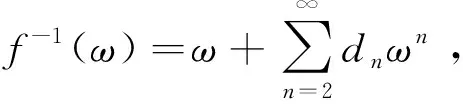从属于叶形域的有界旋转函数逆的Hankel行列式*

郭 栋, 李宗涛

(①滁州职业技术学院基础部，239000，安徽省滁州市;②广州民航职业技术学院数学教学部，510403，广东省广州市)

1 相关定义及引理

令A表示定义在开圆盘U={z:z∈，|z|<1}内的一个解析函数类，其中函数的形式为

(1.1)

令S表示函数类A的在U内单叶的解析子类. 令P表示如下形式的函数类

(1.2)

它满足在U内解析且R(p(z))>0.

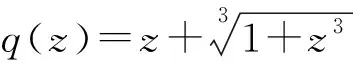
定义1.2 R(q) 表示这样的解析函数类：在单位圆盘 U内解析,规范形式为f(0)=f′(0)=1,满足

取单值分支使得q(0)=1.

Hankel行列式的研究最早见于文献[1],随后出现一系列的拓展研究[2-6].

f的qthHankel 行列式定义如下

(1.3)

其中q≥1,n≥1.

下述研究我们将得到R(q)中的解析函数逆函数的 Hankel 行列式精确上界.为此需要以下引理.

引理1.1[7]如果p∈P 由 (1.2)式给出,那么 |pn|≤2(n∈)，不等式是精确的，极值函数是

引理1.2[8]如果p∈P由(1.2)式给出,那么存在复数x满足 |x|≤1,复数z满足 |z|≤1 使下列式子成立

(1.4)

(1.5)

后面的研究还需要二次多项式的最优值,形式如下

(1.6)

2 主要结果

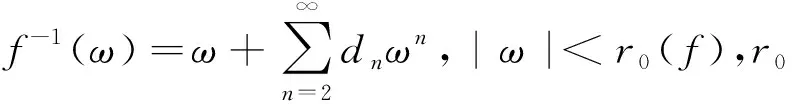
证明因为f∈R(q),所以存在一个U 内的解析自映照w,使得

(2.1)

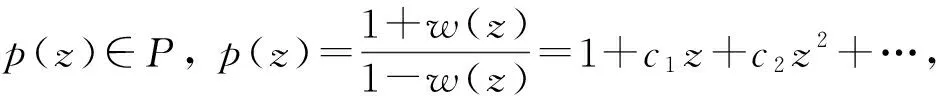
(2.2)

把(2.2)式代入(2.1)式得

(2.3)

简单计算,知

f′(z)=1+2a2z+3a3z2+4a4z3+5a5z4+….

(2.4)

比较 (2.1),(2.3) 和 (2.4)式的系数,可以得到

(2.5)

因为f∈R(q) 是单叶的,所以在圆盘 |ω|

由于f(f-1(ω))=ω,比较系数得

(2.6)

由 (2.5)式和 (2.6)式得

(2.7)

由引理 1.2 得到

令 |c1|=c∈[0,2],|x|=t∈[0,1],由三角不等式即得

现在需要确定G在域 Ω={(c,t):0≤c<2,0≤t≤1} 内的最大值. 首先求G关于t与c的偏导数,

下面研究函数在区域 Ω={(c,t):0≤c<2,0≤t≤1}边界上的驻点.

证明由 (2.7)式,容易得到

(2.8)

利用引理 1.2,如果 |x|<1和 |z|<1,有

因为 |c1|≤2,不妨设c1=c=∈[0,2],|z|=t,利用三角不等式就得到

现在确定函数G在区域Ω={(c,t):0≤c<2,0≤t≤1}内的最大值. 因为

所以G关于t∈[0,1] 是非负函数,

证明由(2.7)式容易得到

(2.9)

证明由引理1.1得|cn|≤2(n∈{1,2,3…}),由引理1.2中的(1.4)式和(1.5)式得到c2和c3的表达式,代入 (2.7)的相关式子,即得证.

(2.10)

对(2.10)式应用三角不等式得

(2.11)

对(2.11)式应用定理2.1,定理2.2,定理2.3和定理2.4的相关结果,即得证.