一类分数阶微分方程边值问题解的存在唯一性
孙晓阳, 徐 润
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
近两个世纪以来,分数阶微积分的研究主要集中在纯数学上. 然而近几十年来,分数阶微分方程在光热系统,电化学,控制,多孔介质,电磁等模型的研究中得到了越来越多的应用. 分数阶微分方程的定性与定量理论已成为当前研究的热点之一.
在对分数阶微分方程定性性质的研究中有很多重要问题,其中一个主要问题是解(或正解)的存在唯一性[1-13]. 目前,许多论文致力于研究分数阶微分方程边值问题解的唯一性. 一些论文利用非线性分析方法研究了微分方程和微分方程组解的唯一性,如Banach压缩原理,混合单调算子不动点定理,极大值定理,u0-正算子和线性算子理论等;另一部分研究了分数阶非线性方程组和分数阶微分系统. Zhenzhen Yue 和 Yumei Zou 研究了依赖于一阶导数分数阶微分方程[14]
其中1<α≤2 且f∈C([0,1]×2,).
在文献[14]的基础上,研究了如下分数阶微分系统
(1)
其中3<α≤4 且f∈C([0,1]×3,,).定义为标准Riemann-Liouville积分的导数
其中n-1≤α (H)f:[0,1]×3→是一个连续函数且存在常数A,B,C>0 使得下式成立 |f(t,u1,v1,w1)-f(t,u2,v2,w2)|≤A|u1-u2|+B|v1-v2|+C|w1-w2|,t∈[0,1]. 定义1.1 函数f:[0,1]→的α>0 阶Riemann-Liouville分数阶积分由以下式子给出 且右侧定义在(0,∞) 上. 定义1.2 本文定义以下3个函数 (2) 引理1.1[5]令G如(2)式所示,则有下式成立 为了证明以下定理,通过计算得到了下面两个式子 tα-2[B(α-1,α-2)+2t2α-3B(α-1,α-1)]≤ tα-2[B(α-1,α-2)+2B(α-1,α-1)], tα-2B(α-2,α-2)+2t2α-4B(α-2,α-1)≤ tα-2[B(α-2,α-2)+2B(α-2,α-1)], 则E1×E2×E3是范数 ‖(u,v,w)‖E1×E2×E3,‖(u,v,w)‖E1×E2×E3的Banach空间且被定义为 ‖(u,v,w)‖E1×E2×E3=max{‖u‖E1,‖v‖E2,‖w‖E3}. 令w=u″,v=u′,由系统(1)得 其中1<α-2≤2. 定义算子T如下所示 T(u,v,w)=(T1(u,v,w),T2(u,v,w),T3(u,v,w)),(u,v,w)∈E1×E2×E3. T1,T2,T3分别定义为 (3) 对于 (u,v,w)∈E,由引理1和(H)条件,得出 对于一个常数θ>0. 这表明T1在E中有很好的定义. 也能证明T2和T3有很好的定义. 因此,边值问题解的存在性等价于T在不动点的存在性. 接下来,只考虑Banach空间E=E4×E2×E3的不动点. 引理4[14]令a,d∈[0,1),b,c∈[0,+∞),且满足 (1-d)(1-a)>bc. 那么系统 有一个解 (λ,θ), 且λ∈(0,1),θ>0. 首先给出以下记号 a21=A[B(α-1,α-2)+2B(α-1,α-1)],a22=B[B(α-2,α-2)+B(α-2,α-1)], a23=C[B(α-3,α-2)+B(α-3,α-1)]. 现在通过Banach压缩映射原理来证明解的唯一性. 定理1 假设条件 (H) 成立,a11,a12,a13,a21,a22,a23, 满足下列条件 a11<1,a22+a23<1,(1-a11)[1-(a22+a23)]>(a12+a13)a21, 则BVP (1) 有唯一解. 证明由引理4,存在λ∈(0,1) 和θ>0,使得以下系统成立 (4) 在E=E4×E2×E3上应用压缩映射原理. 设 由 (3),(4) 和条件 (H),有 由 ‖·‖E4的定义,有 类似的,有 上述结果是由不动点定理给出的解的唯一性结果. 在上述过程中,我们遇到的困难是如何用引理4来处理高阶微分方程. 本文将w化为常数M来处理这类依赖于二阶导数的分数阶微分方程唯一解的问题.1 准备工作


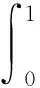
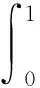
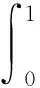






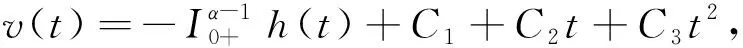

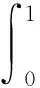




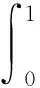
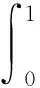


2 主要结果



