三点法测直径的误差分析及方案优化

梁 雄，赖国忠

(龙岩学院 福建龙岩 364000)

塞曼效应为研究原子结构提供了重要途径[1]，横向塞曼效应被用于检测大气汞[2]和烟气汞[3]，除此之外，塞曼效应还可用于测量超强磁场[4]。近代物理实验课程常开设塞曼效应实验，用于测量电子的荷质比，测量过程有个主要任务就是测量干涉环的直径，测量过程数据比较多，耗时长。人们为了便于观测或减轻观测任务，提出了各种观测方法：用阿贝比长仪观测分裂谱底片[5]，利用五点中心测量法[6]优化了测量过程，基于CCD传感器技术，结合数字图像处理技术提出了半自动[7-8]或自动[9-10]测直径，也有基于LabVIEW结合手动取三点测直径[11]。 虽然出现了全自动测直径的方法，但是在学生实验中采用手动测直径，一方面可以增强学生的动手能力，另一方面可以加深对物理规律的理解。三点法还被应用到19JPC微机型万用工具显微镜测样品上的圆斑或圆孔的直径，其组成与工作原理可参见文献[12]。在塞曼效应实验的测量过程中，发现大多数学生使用FD-FZ-C法拉第效应塞曼效应综合实验仪时，常常按图1 (a)或(b)所示的方式来选取A、B和C三点，只有少数学生采用如图1(c)那种方式来取点。

图1 三点取法对比示意图

考虑到选点时受人眼(或仪器)分辨率的影响导致的位置误差，这三种选点方式是否具有一样的直径测量精确度？本文从误差传递公式及几何知识来分析所取三点的连线构成什么样的三角形时，直径测量误差最小以及这三点选取误差各自对直径测量精确度有怎样的影响,最后应用Matlab软件模拟干涉环的测量来验证讨论所得的结论。

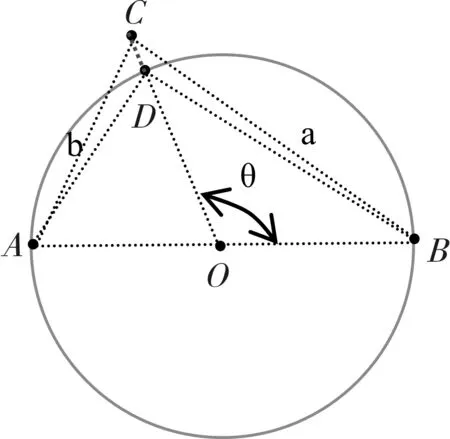
图2 直角顶点偏离示意图

1 三点法测直径原理及其优化

1.1 三点法测直径原理

如图1所示，在待测圆上任取三点A、B和C，该圆是三角形ABC的外接圆，弦AB的长度设为l， ∠ACB=α(下文中α均指∠ACB)，容易由正弦定理将待测圆的直径表示成：

d=l/sinα，

(1)

除了按式(1)计算直径外，还可根据所取的三点要满足圆的方程而列出三个方程，从该方程组可先求得圆心坐标，再求出圆心到这三点中的任一点之间距离即可求得相应环的半径[11]。一旦从待测圆弧上选定三点，不同计算法求解的直径结果是一样的，即与真值之间的偏差也相同。估算误差时，由于不同计算方法对应的误差传递公式不同，估算误差也会不完全一致，但是它们估算的误差水平应是相当的，所以为了便于讨论选点位置的误差对直径结果的影响，本文采用式(1)的误差传递公式来讨论三点应该在圆上的什么位置选取可以将直径的测量误差最小化，而后一种方法便于在Matlab编程求解直径，因此模拟测量过程将采用后面这种方法验证误差分析所得的优化方法。

1.2 三点法测直径误差及三点最佳取法

由误差传递公式容易求出(1)式的直径测量误差为：

(2)

其中uc(l)和uc(α)分别代表测量弦长l和α的综合不确定度。结合图1可知，弦长l越大，角α就越接近90°，当弦长取最大值时，有l=d和α=90°，在等精度测量的前提下，此时上式根号里头两项都达到最小。由此看来，三点法测直径时A、B两点应尽可能选取在直径端点位置，它们与另外一点C的连线构成直角三角形，此时直径的测量误差最小。

为了便于讨论直角顶点C的误差对直径的影响，假设AB准确地落在半径为R待测圆直径的端点上(即AB=2R)，而选取顶点C受人眼分辨率或仪器分辨率的影响将会导致该点偏离待测圆，距离记作Δ(如图2中线段CD)，因此选取C点误差会导致角α与直角存在一定的偏差。

不妨假设圆上不同位置选取C点时不确定度Δ相当，令∠BOC=θ，∠BCO=α1，OC记作r。 在三角形BOC中由正弦定理得：

可求得

r=Rsin(θ+α1)/sinα1，

两边取微分得(在此假设θ为常数),并令dr=Δ，α1≈(π-θ)/2，整理得：

(3)

在三角形AOC中,令∠ACO=α2，同理可求得：

(4)

考虑判断误差Δ通常较小，即R≫Δ或Δ/R≪1，此时角α与直角有一个较小的偏离ε1：

(5)

其中负号含义：当Δ>0，即选取直角顶点C在圆外，则导致α略小于π/2；反之，导致α略大于π/2.由此可见：倘若在圆弧上A、B两点邻近区域选取直角顶点C时，此时θ接近0°或180°，在同样半径偏离Δ情况下，将导致较大的角度误差ε1。而在圆弧上θ=90°的位置选择直角顶点C，结合图2几何关系可知：综合误差公式(2)的分析结果，所选三点的连线构成一个等腰直角三角形，此时由选点位置误差造成α角的误差最小：ε1=-Δ/R， 将其代入误差传递公式(2)可得测量直径的相对误差：

(6)

式(6)推导中应用了cotα=cot(π/2+ε1)≈-ε1。

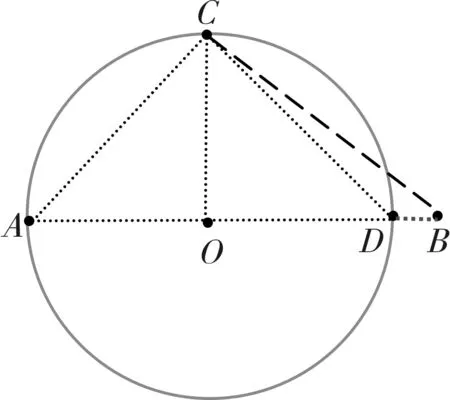
图3 直径方向上点偏离圆对角度的影响

1.3 直径两端取点对直径测量误差的影响

在直径端点处取两点A、B，考虑这两点在圆弧上位置具有对称性，它们位置误差相当，在此仅以B点为例进行说明。如图3所示，假设A、C两点准确无误地落在圆上，在待测圆上位置D选择B时，由于判断误差将会沿着直径方向偏离到B点(注：也有可能落在圆内)，偏离距离记作Δ，容易知道∠ACB比90°大，导致直角误差ε2。

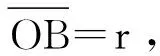
(7)

对式(7)取微分可得：

(8)

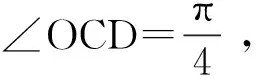
(9)

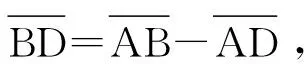
(10)

2 干涉环直径测量模拟

由于实际的塞曼效应实验中无法事先确切地知道法布里—珀罗腔(F-P腔)干涉图样中干涉环的直径真值，这将造成无法计算每次测量误差，以及难以判断多次测量算术平均值哪种取点方法更接近真值。为了克服这些不便，利用Matlab模拟塞曼效应的干涉图样，各参数按照文献[13]。具体选取情况：F-P腔的反射率设为90%，折射率n=1.5，腔厚d=5.55 mm，成像透镜焦距f=200 mm，波长λ=555 nm，模拟F-P干涉图样的结果如图4所示。测量过程选取图4中最接近中央亮斑的干涉环，其直径可由理论计算得：d0=3.266 mm(将它视作真实值，即可求出测量误差)，应用软件中ginput命令按图1中三种采点方式取点，按从左到右将这三种方式简称M1、M2和M3，每种方法取30组(其中每组数据由三个点坐标组成)，即每种方法测量圆直径30次。

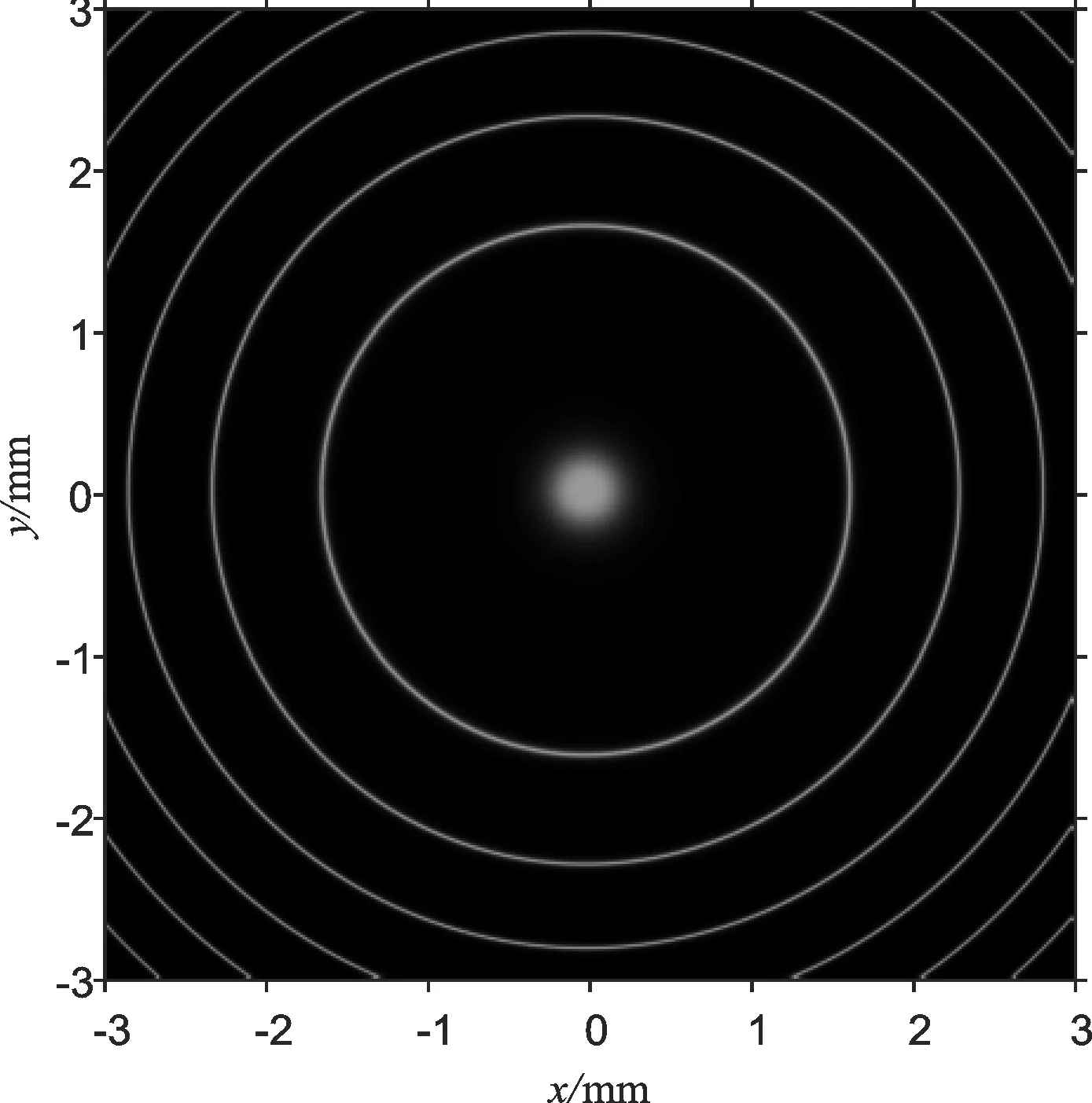
图4 F-P腔干涉模拟图

将相应的直径测量值减去理论值即可求得每次测量误差，以数据编号i为横坐标，将三种取点方式的直径测量误差绘制成曲线(见图5(a))：M1测量误差曲线对应左侧纵坐标轴u(d)，另外两种方式M1、M3测量误差曲线对应右侧纵坐标轴u1(d)。

从图5(a)中可以看出，M1和M2方式测量结果误差的波动幅度都比较大，而M3方式取点每次测得直径与理论值之间的偏差都比较小。这三种取点方法测得直径的平均值分别为3.371 mm、3.272 mm和3.270 mm，其中M3平均值最接近待测干涉环直径的真值(3.266 mm)。此外用标准偏差来衡量波动幅度，它们分别为： 0.730 mm(M1)、0.007 mm(M2)和0.004 mm(M3)。这是因为：M1取点所测的弦长比直径小得多，按照式(1)可知测得直径必须按某个比1大得多的因子(1/sinα)放大后求得，放大过程同样将弦长l的测量误差进行了放大，而M2与M3虽然都有较大的弦长(甚至接近直径)，但由于方式2中直角顶点非常靠近直径端点，此时由于直角顶点选取误差导致α偏离90°较大，导致M2的直径测量误差要大于M3的误差，这与前面误差分析所得的结论完全一致。

三种方式检测的圆心坐标情况，用测量所得的圆心坐标与实际圆心坐标(0,0)之间的距离e衡量圆心的检测误差，如图5(b)所示，对比后容易发现：采用等腰直角三角形的方式取点，M3的圆心检测误差e要比其他两种方式取点所得的结果要小得多。

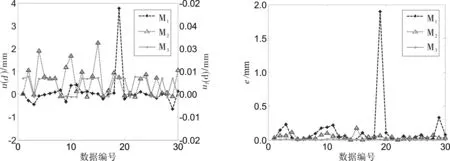
(a) 直径测量误差曲线 (b) 圆心测量误差曲线

3 结论

应用三点法测量待测圆(例如干涉环)的直径或圆心，采用等腰直角三角形的选点方式具有较高的精确度。此外，建议用FD-FZ-C法拉第效应塞曼效应综合实验仪做塞曼效应实验时，首先在干涉图样中选取较大的干涉环，按照优化后的方法测定环心坐标，再沿着垂直直径AB方向在每个待测环上选取一个点，这样可以比较精确地测定相应待测环直径，同时也有利于减小电子的荷质比测量误差。顺便提一下，在估算选点的误差对直径测量影响时，按照优化取点方式，直径测量误差主要来源于直径端点处所取两点的位置误差，而直角顶点的位置误差对直径测量精确度影响比较小，基本可以忽略。