基于数理统计方法的铁路隧道衬砌质量缺陷分析
柴子贺
(中铁工程设计咨询集团有限公司,北京 100055)
1 概述
1.1 研究现状
随着我国铁路事业的迅猛发展,铁路隧道的建设长度位居世界第一[1]。然而,相当比例的隧道存在不同程度的缺陷[2]。隧道衬砌缺陷会导致隧道结构承受偏压荷载,造成应力集中现象,使得缺陷处成为衬砌结构破坏的重点[3]。
地质雷达法是一种无损检测方法,具有检测精度高、效率快、成本低等优势,在隧道衬砌质量无损检测中广泛应用[4]。目前,常见的做法是对单个缺陷进行描述,缺少对全部缺陷全面深入地分析,以及对缺陷分布内在规律的研究。
数理统计方法已广泛应用于土力学[5-6]、水文[7-8]、边坡稳定[9]等工程类技术研究中,跨学科方法对推动相关研究起到了巨大作用。如李刚等结合数理统计方法,检验不同成因沉积土物理力学指标的分布特征[5];朱焕珍等采用正态信息扩散法,推断出大样本岩土抗剪强度参数的概率密度函数[6];王林等提出一种基于贝叶斯理论的土水特征曲线模型比选和参数识别方法[7];王东等提出一种基于Lilliefors检验的边坡临滑时刻的动态识别方法[8]。此外,数理统计方法在混凝土强度的分布特征研究方面也有所应用[10-11]。因此,将数理统计方法应用于隧道衬砌质量检测,对探究缺陷内在分布规律意义重大。
1.2 工程背景
某在建高速铁路为双线,设计行车速度为350 km/h,线间距为5.0 m,最小曲线半径为7 000 m,困难为5 500 m,最大坡度为20‰。工程地处丘陵地带,地形起伏较大,局部陡峭。出露地层有第四系全新统、白垩系、震旦系,主要岩性有泥质粉砂岩、砂岩、含砾砂岩、变质砂岩等。地表水主要为溪沟水,地下水主要为基岩裂隙水。
隧道断面如图1所示,采用二次复合衬砌形式,Ⅱ级围岩段落衬砌为C30素混凝土,厚35 cm;Ⅲ级围岩段落衬砌为C30素混凝土,厚40 cm;Ⅳ级围岩段落衬砌为C35钢筋混凝土,环向钢筋为HRB400,间距20 cm,厚45 cm;Ⅴ级围岩段落衬砌为C35钢筋混凝土,环向钢筋为HRB400,间距20 cm,厚50 cm。
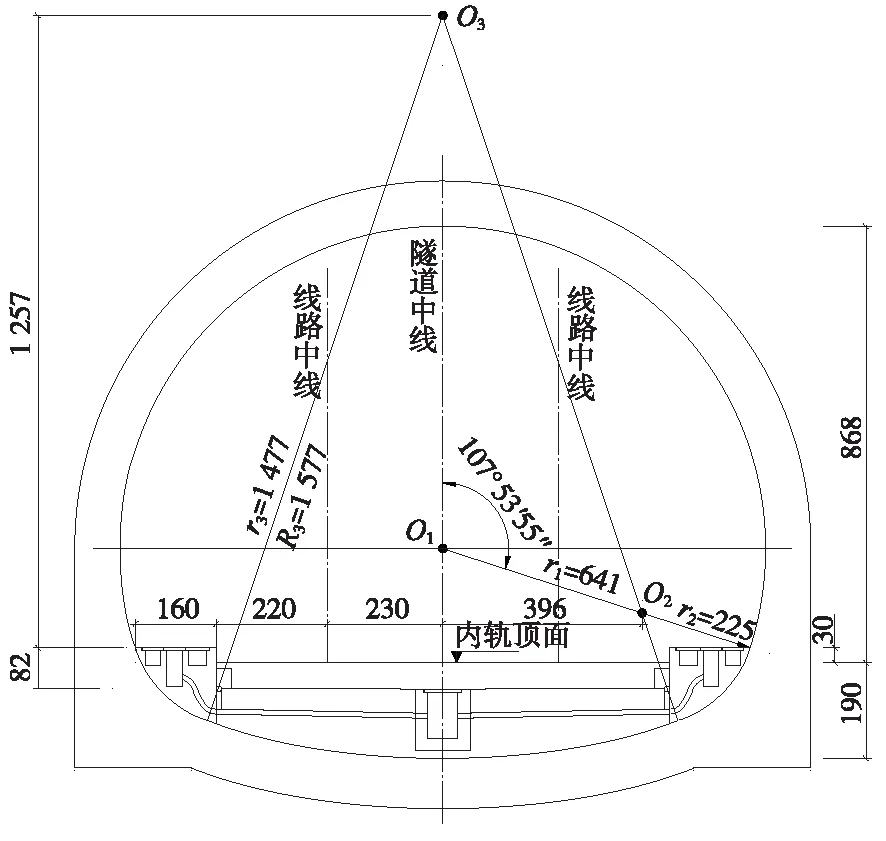
图1 隧道断面示意(单位:cm)
2 衬砌缺陷类型及测线部位的分布规律
2.1 地质雷达法检测概况
利用地质雷达法对某在建铁路工程14座隧道进行二次衬砌质量无损检测,沿二衬表面布置5条测线[12],分别为拱顶1条、左右拱腰各1条及左右边墙各1条,共发现285个缺陷。缺陷类型有空洞、欠厚空洞、欠厚、不密实共4种。以下主要研究衬砌缺陷的纵向长度及径向尺寸。其中,缺陷总长度与该测线检测长度的比值为该测线的缺陷率。对于欠厚空洞、脱空、不密实缺陷,衬砌内表面距初支表面的最大距离为其缺陷径向尺寸;对于欠厚缺陷,衬砌最薄处与设计厚度的差值为其缺陷径向尺寸。
2.2 不同测线缺陷样本的分布规律
对地质雷达法检测发现的285个衬砌质量缺陷进行分析,研究不同测线部位的缺陷率、不同缺陷类型在各测线缺陷中所占比例及不同测线部位的缺陷径向尺寸的平均值、标准差、最大值等相关特征值的变化规律。
(1)不同测线部位的缺陷率
表1是地质雷达法检测某铁路工程14座隧道不同测线衬砌缺陷率的统计数据,并根据表1数据绘制图2。
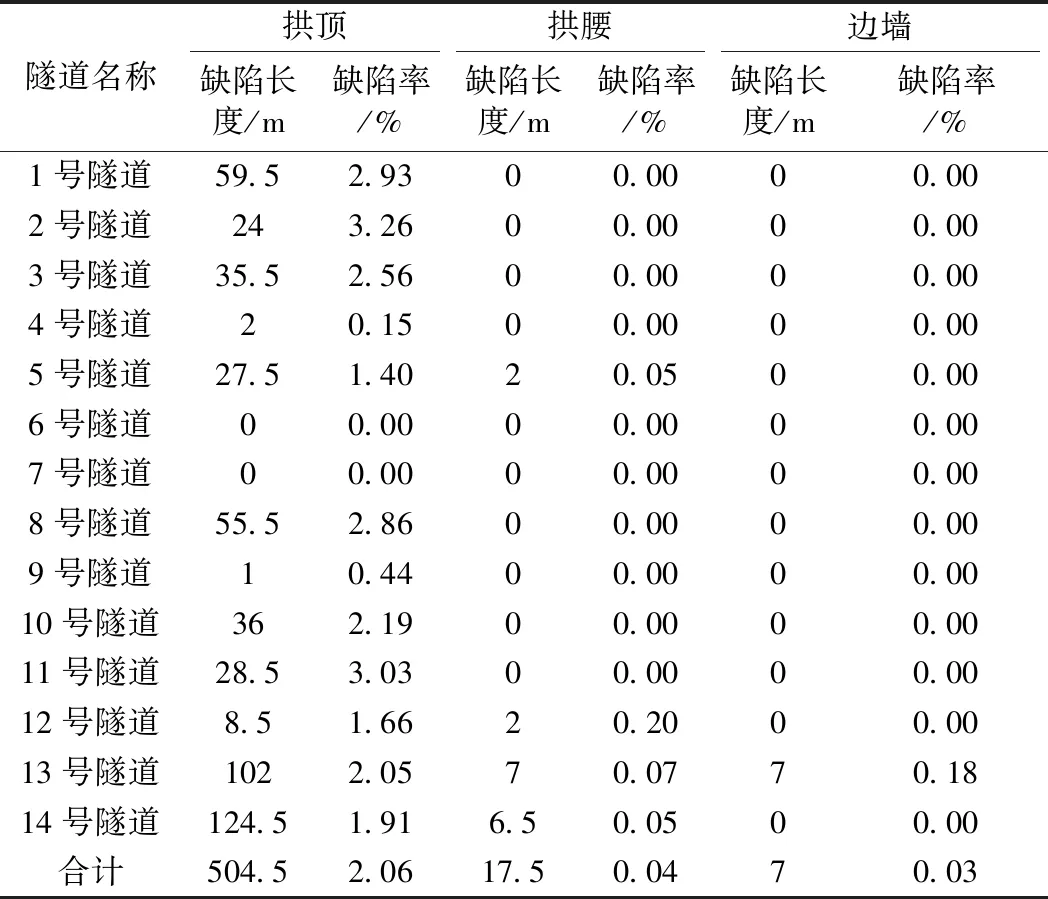
表1 隧道衬砌缺陷分布情况
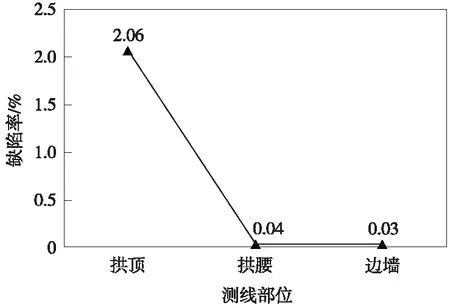
图2 各测线部位缺陷率
由表1及图2可知,从已知缺陷样本来看,拱顶缺陷率最高,为2.06%;拱腰、边墙缺陷率分别为0.04%、0.03%。
建议在后续的施工过程中,注意拱顶部位的施做,改进工艺工法,减少拱顶部位的缺陷率。在综合考虑质量控制、工程成本等情况下,可适当减少拱腰及边墙部位的测线,适当增加拱顶部位的测线,使检测更具针对性。
(2)不同缺陷类型在各测线缺陷中所占比例
表2是不同缺陷类型在不同测线缺陷中所占的比例统计数据,根据表2数据绘制图3。
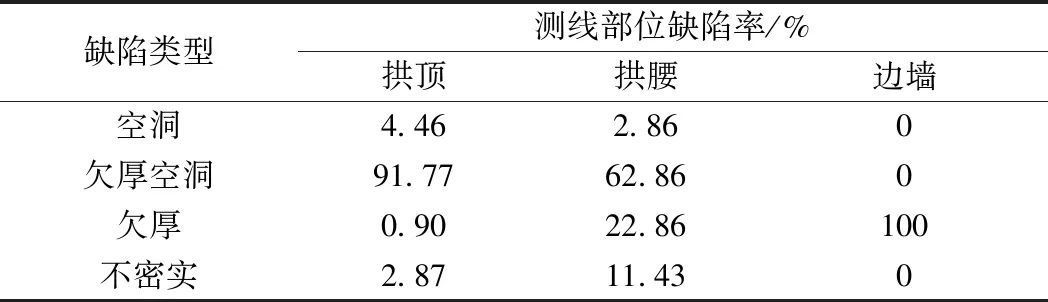
表2 不同缺陷类型在各测线缺陷中所占比例
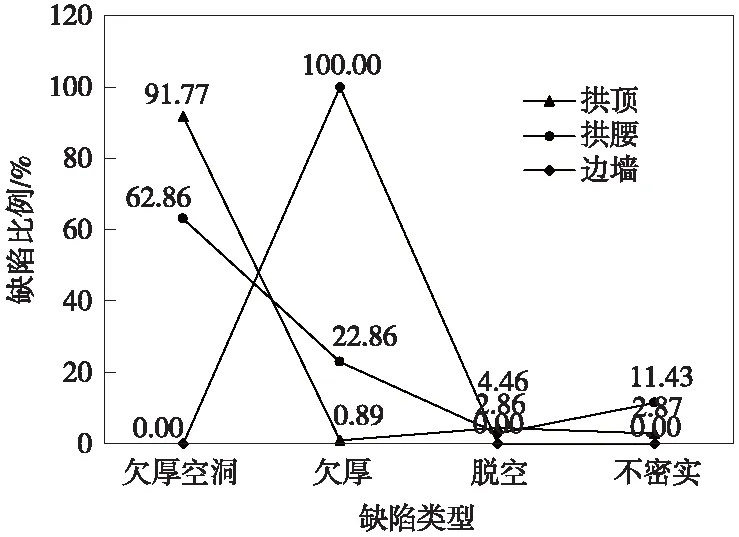
图3 不同缺陷类型在各测线缺陷中所占比例
由表2及图3可知,不同测线部位产生的主要缺陷类型不同。拱顶部位的缺陷中,欠厚空洞占比最高,为91.77%,欠厚占比最低,为0.90%;拱腰部位的缺陷中,欠厚空洞占比最高,为62.86%,空洞占比最低,为2.86%;边墙部位的缺陷中,只发现欠厚缺陷,占比100%。
以拱顶、拱腰、边墙为序,欠厚空洞占该测线缺陷的比例越来越低,最高为91.77%,最低为0%。欠厚所占比例越来越高,最低为0.89%,最高为100%。
建议在后续施工过程中,改进工艺工法,拱顶部位应着重注意避免欠厚空洞缺陷的产生;拱腰部位着重注意避免欠厚空洞及欠厚的产生;对边墙部位,着重注意避免欠厚缺陷的产生。
(3)不同测线部位的缺陷径向尺寸最大值、平均值及标准差等特征值规律
表3为地质雷达法检测发现的该在建铁路工程14座隧道共285个衬砌缺陷的径向尺寸样本观测值,图4为根据表3得出的各测线部位的缺陷径向尺寸相关特征值。
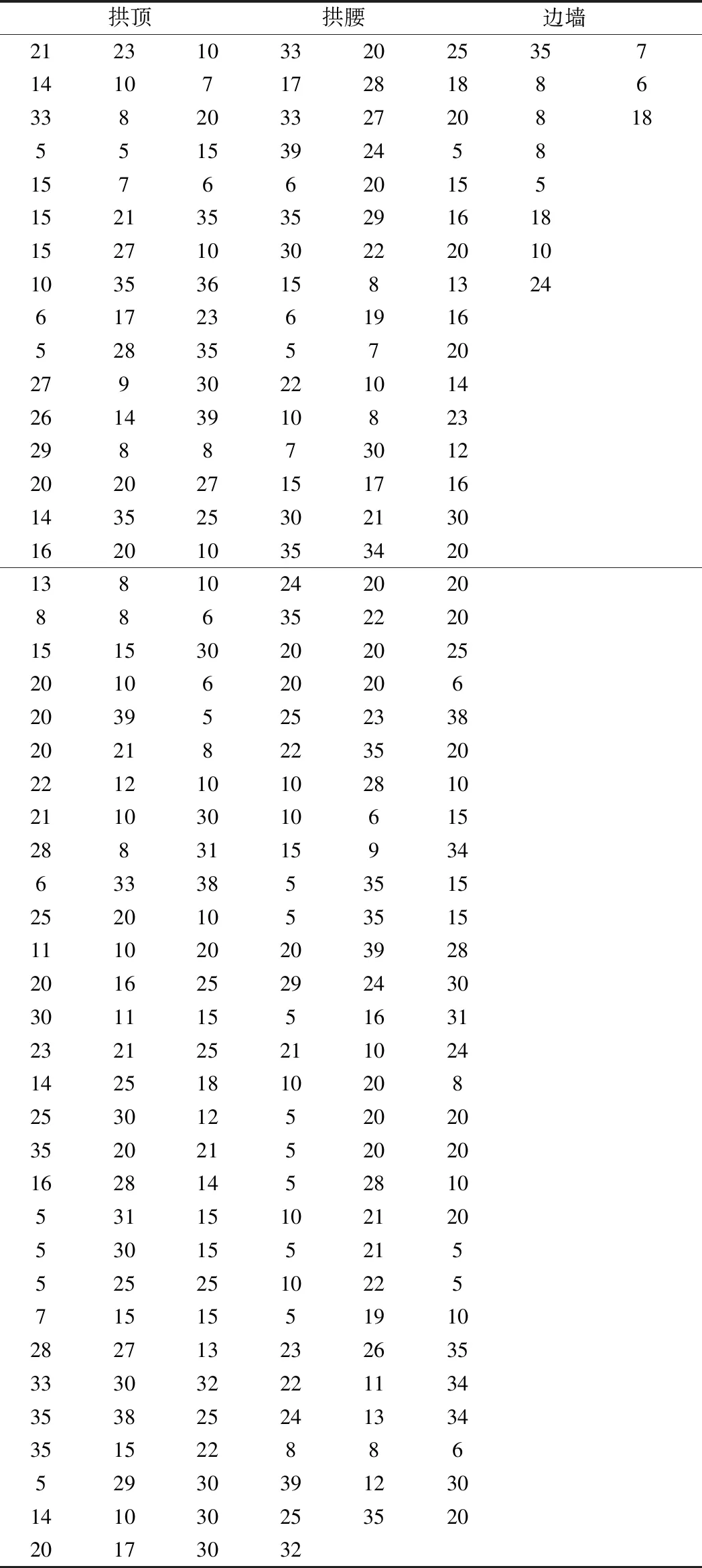
表3 缺陷径向尺寸285个样本观测值 cm
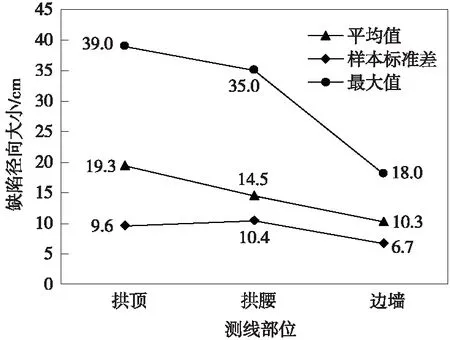
图4 不同测线部位的缺陷径向尺寸特征值
由表3及图4可知,就缺陷径向尺寸的最大值而论,拱顶、拱腰及边墙部位分别为39.0,35.0,18.0 cm;对于缺陷径向尺寸的平均值,拱顶、拱腰及边墙部位分别为19.3,14.5,10.3 cm;对于缺陷径向尺寸的样本标准差,拱顶、拱腰及边墙部位分别为9.6、10.4及6.7。
对于缺陷径向尺寸的最大值,拱顶、拱腰及边墙部位依次减小,对于缺陷径向尺寸的平均值,拱顶、拱腰及边墙部位依次减小。对于缺陷径向尺寸的样本标准差,拱腰部位最大,拱顶次之,边墙最小,说明拱腰部位的缺陷径向尺寸离散性最大,拱顶次之,边墙最小。
3 衬砌缺陷径向尺寸总体数理统计
3.1 衬砌缺陷径向尺寸总体与样本的设定
将该铁路工程14座隧道衬全部砌缺陷的径向尺寸视为总体X。已检测出的285个缺陷,径向尺寸X1,X2,…,X285为总体X的一个样本x,其样本容量n=285。
表3中所列即为285个衬砌径向尺寸样本x(下文简称样本x)的观测值。每个缺陷为相同的条件下独立发现的,且都是与衬砌缺陷径向尺寸总体X(下文简称总体X)具有相同分布的随机变量。有
样本均值
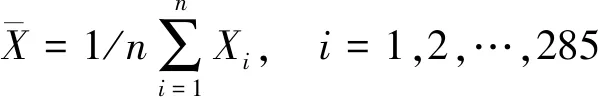
(1)
样本方差
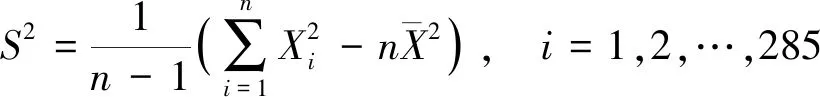
(2)
样本标准差
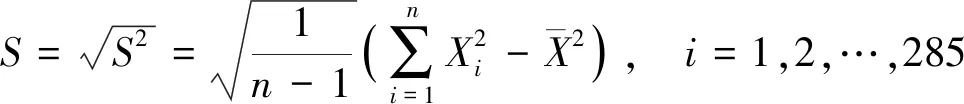
(3)
样本k阶中心矩

(4)
3.2 总体X正态性检验
正态分布是自然界最重要的分布,对于该在建铁路工程14座隧道检测发现的285个缺陷的径向尺寸,需判断其样本x所代表的总体X是否符合正态分布,根据GB/T4882—2001《数据的统计处理和解释正态性检验》,采用偏度及峰度检验法进行正态性检验[13-16]。
(1)总体X偏度及峰度检验统计量
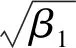
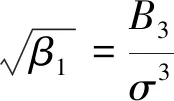
(5)
峰度β2是标准化的四阶中心矩,有
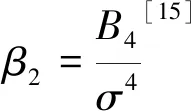
(6)
总体X的偏度和峰度的检验统计量分别为
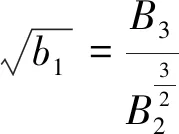
(7)
和
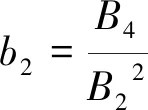
(8)
式中,B2,B3,B4分别为样本值的2阶,3阶,4阶中心矩。
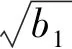
由于缺陷的径向尺寸为非负值,因此对总体X的正态检验采用有方向检验。
①给出检验零假设和备择假设
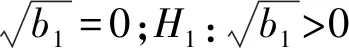
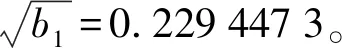
③给定显著水平α=0.05,根据给定的α和样本容量285,查表得p的分位数为0.24,其中,p=1-α。
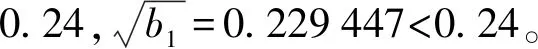
(3)总体X的峰度b2有方向检验
由于样本观测值是由地质雷达仪器检测发现的,认为观测值的离散程度受到影响,因此备择假设为H1:b2>3。
①给出检验零假设和备择假设
H0:总体X为正态分布即b2=3;H1:b2>3。
②将表3所列样本x的观测值X1,X2,…,X285代入式(4)和式(8)计算得B4=17 111.78,B2=8 573.577,峰度b2=1.995 874。
③给定显著水平α=0.05,根据给定的α和样本容量285,查表得b2的p分位数为3.49,其中,p=1-α。
④如果统计量b2超过p分位数,则在显著性水平α下拒绝零假设。
由于b2=1.995 874<3.49,在α=0.05显著水平下不拒绝零假设,即样本x所代表的总体X服从正态分布。
综合偏度和峰度检验结果,在建铁路工程14座隧道共285个缺陷径向尺寸样本x所代表的总体X服从正态分布。
3.3 总体X参数估计
(1)总体X的均值μ区间估计
上文已证明总体X服从正态分布,令总体为X(μ,σ2),其中,μ为总体均值,σ2为总体方差,均为未知。给定显著性水平α=0.05,且已知样本容量n=285。
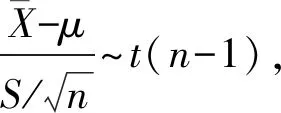
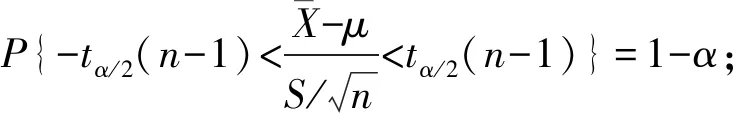
在总体方差σ2未知的情况下,得总体均值μ的一个置信区间为
将表3所列样本x的观测值,代入公式,在给定显著性水平α=0.05下,计算得总体X均值μ的一个置信区间为(17.99,20.24)。
其物理意义为在给定显著性水平α=0.05下,该在建铁路工程14座隧道衬砌缺陷径向尺寸的总体X的均值μ落在(17.99,20.24)区间的概率为95%。
(2)总体X的方差区间估计
由于总体X均值μ未知,σ2的无偏估计为S2,给定显著性水平α=0.05的情况下,有((n-1)S2)/σ2~χ2(n-1),且该式右端分布不依赖于任何未知参数。
即

(9)
得到总体方差σ2的一个置信水平为1-α的置信区间为
将表3所列样本x观测值,代入公式,在给定显著性水平α=0.05下,计算得总体X方差σ2的一个置信区间为(76.63,110.71)。
其物理意义为在给定显著性水平α=0.05下,该在建铁路工程14座隧道衬砌质量缺陷径向尺寸总体X的方差σ2落在(76.63,110.71)区间的概率为95%。
3.4 单因素方差分析
(1)单因素方差分析原理
单因素方差分析是检验在一种因素影响下,两个以上总体的均值彼此是否相等的一种统计方法[17]。表4中所列样本x观测值,分布在Ⅱ级、Ⅲ级、Ⅳ级和Ⅴ级围岩段。
为分析围岩等级情况对隧道衬砌缺陷径向尺寸的影响,本节以拱顶测线检测发现的缺陷为例,对Ⅱ-Ⅴ级围岩因素对缺陷径向尺寸的影响进行分析。
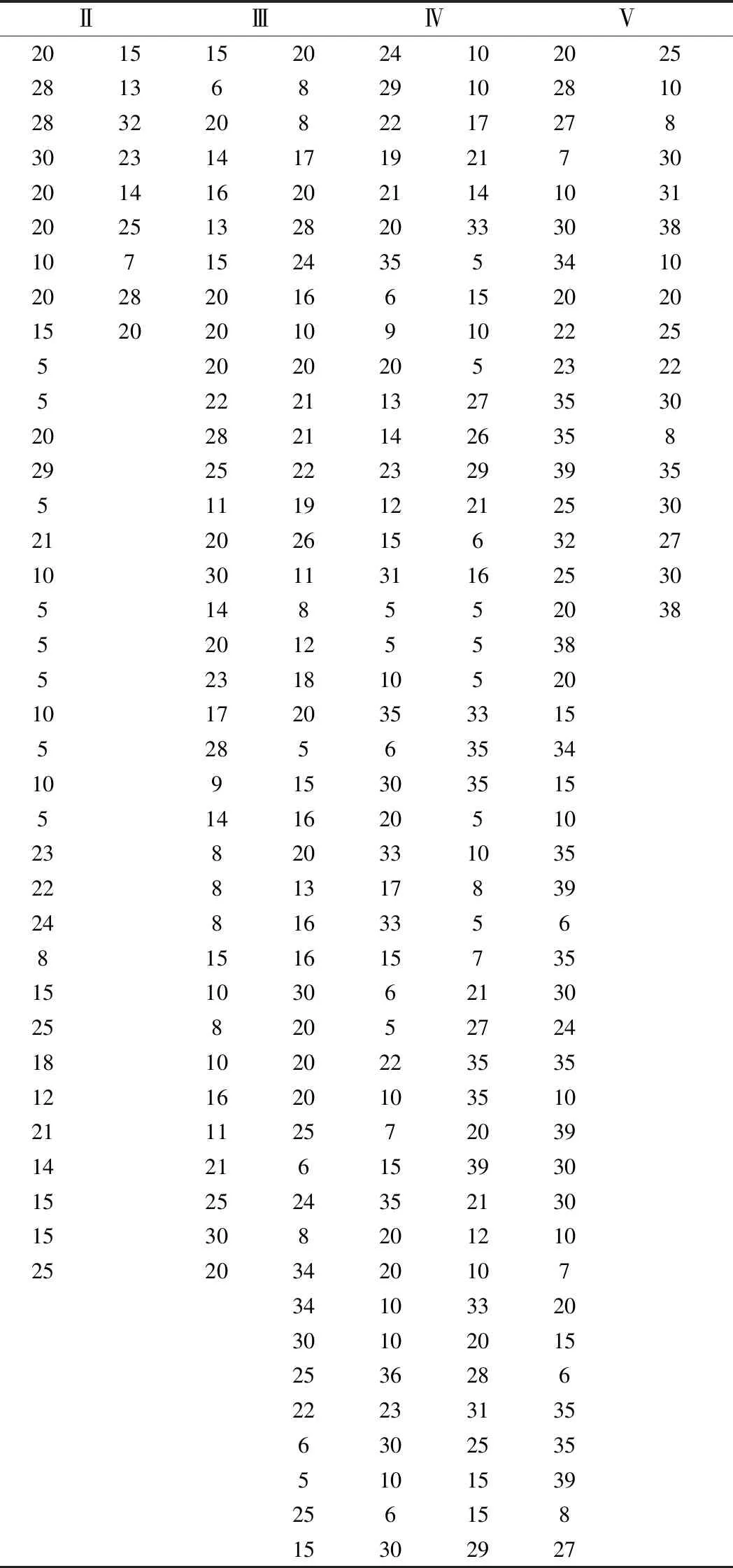
表4 分围岩级别缺陷径向尺寸样本值 cm
围岩等级因素分别记为A1,A2,A3,A4,在每个水平Ai(i=1,2,3,4)下,考察指标看成一个总体Xi(i=1,2,3,4),且Xi~N(μi,σ2),水平Ai(i=1,2,3,4)下,进行ni次独立试验,样本记为Xij,i=1,2,3,4,j=1,2,…,ni,Xij~N(μi,σ2)且相互独立[17]。
(2)围岩等级因素方差分析步骤
①建立假设检验
零假设为H0:μ1=μ2=μ3=μ4,备择假设为H1:μ1,μ2,μ3,μ4不全相等。
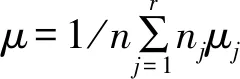
因此,数学模型为
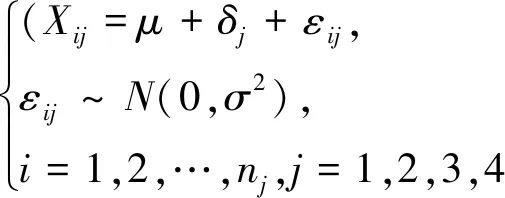
(10)
②构造检验统计量
引入总偏差和
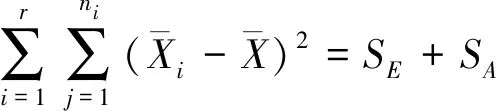
(11)
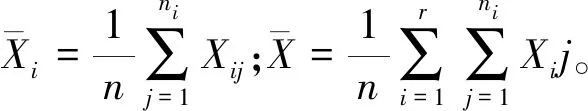
故构造检验统计量为
③假设检验问题的拒绝域
本文给定显著性水平α=0.05,在给定的α显著性下,检验假设问题的拒绝域为
F=(SA/(r-1))/(SE/(n-r))≥
Fα(r-1,n-r)
(12)
④计算检验统计量
a.Ⅱ、Ⅲ及Ⅳ级围岩段落拱顶缺陷径向尺寸总体均值差异性检验
对Ⅱ、Ⅲ及Ⅳ级不同围岩段落发现的拱顶缺陷径向尺寸总体X1,X2,X3的各自样本观测值进行计算,结果见表5、表6。
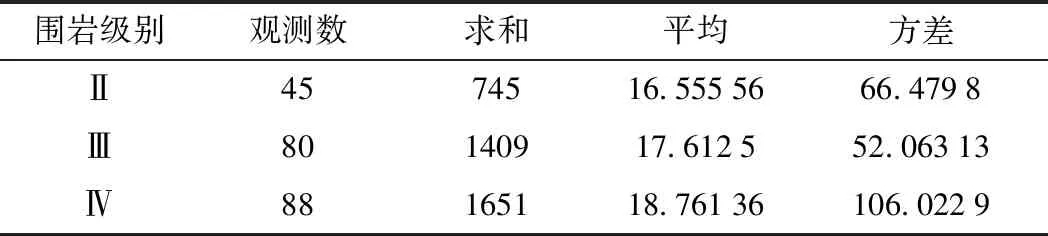
表5 Ⅱ、Ⅲ、Ⅳ级围岩方差综合

表6 Ⅱ、Ⅲ、Ⅳ级围岩方差分析
由表5、表6可知,在给定显著性α=0.05水平下,检验统计量F=0.987 651 b.Ⅱ、Ⅲ、Ⅳ及Ⅴ级围岩段落拱顶缺陷径向尺寸总体均值差异性检验 对Ⅱ、Ⅲ、Ⅳ及Ⅴ级不同围岩段落拱顶部位发现的衬砌缺陷径向尺寸总体的样本观测值进行计算,结果见表7、表8。 表7 Ⅱ、Ⅲ、Ⅳ、Ⅴ级围岩方差综合 表8 Ⅱ、Ⅲ、Ⅳ、Ⅴ级围岩方差分析 可知在给定显著性α=0.05水平下,检验统计量F的值F=8.882 052>F0.05(3,270)=2.638 036,所以拒绝零假设,认为Ⅱ级、Ⅲ级、Ⅳ级和Ⅴ级不同围岩段落发现的拱顶部位衬砌质量缺陷径向尺寸总体的均值有显著差异。 综上可知,在拱顶部位,在给定显著性水平α=0.05下,Ⅱ、Ⅲ、Ⅳ级围岩段落的衬砌缺陷径向尺寸的总体均值无显著差异,V级围岩段落的衬砌缺陷径向尺寸总体的均值与Ⅱ、Ⅲ、Ⅳ级围岩段落有显著差异,且大于Ⅱ、Ⅲ、Ⅳ级围岩段落。 (1)地质雷达法检测的缺陷样本,拱顶缺陷率为2.06%,拱腰缺陷率为0.04%,边墙缺陷率为0.03%。 (2)在拱顶、拱腰、边墙部位的缺陷样本中,欠厚空洞缺陷所占比例越来越低,最高为91.77%,最低为0。欠厚缺陷所占比例越来越高,最低为0.89%,最高为100%。 (3)对于缺陷径向尺寸的最大值,拱顶、拱腰及边墙部位依次减小;对于缺陷径向尺寸的平均值,拱顶、拱腰及边墙部位依次减小;对于缺陷径向尺寸的样本标准差,拱腰部位最大,拱顶次之,边墙最小。 (4)文中列出的在建铁路工程14座隧道共285个缺陷的径向大小样本观测值所代表的总体符合正态分布。 (5)在给定显著性水平α=0.05下,该在建铁路工程14座隧道衬砌质量缺陷径向大小总体均值μ的一个置信区间为(17.99,20.24),总体方差σ2的一个置信区间为(76.63,110.71); (6)在给定显著性水平α=0.05下,Ⅱ、Ⅲ、Ⅳ级围岩段落的衬砌缺陷径向尺寸的均值无显著差异,Ⅴ级围岩段落的衬砌缺陷径向尺寸的均值与Ⅱ、Ⅲ、Ⅳ级围岩段落有显著差异,且大于Ⅱ、Ⅲ、Ⅳ级围岩段落。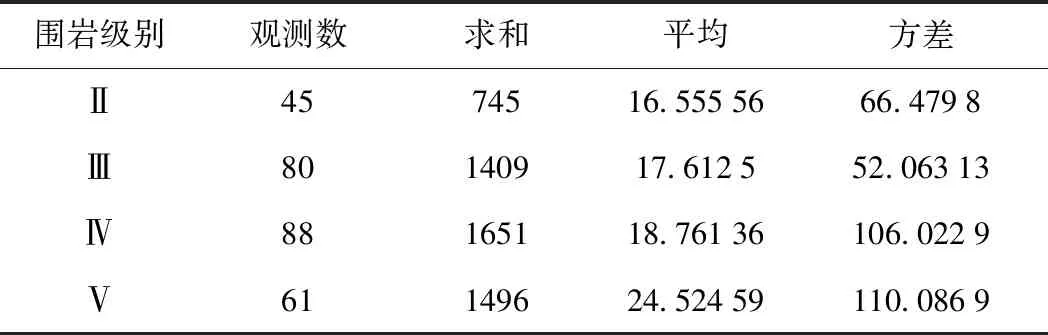

4 结论

