一种连通合并优化的k近邻密度峰值聚类改进算法*

廖丽敏 荣章权 王洋

(广东顺德工业设计研究院(广东顺德创新设计研究院),广东佛山 528311)

0 引言

聚类是机器学习领域中无监督学习的一类算法,目标是将一组数据分成不同类簇,使得类簇内存在较大相似性,类簇间存在较大相异性[1]。大数据时代是数据分析方法的革新时代[2],面对越来越复杂、多样的数据,聚类作为重要的数据分析方法之一,近年来也越来越受关注。聚类中有很多经典的算法:基于距离划分的k-means算法、基于网格的STING和CLIQUE算法和基于密度划分的DBSCAN算法等。近年来随着深度学习算法的发展,也出现了诸如SOM等的人工神经网络聚类算法。现在学者们也逐渐开始对高维、庞大数据的复杂网格聚类进行相关研究。

2014年,Rodriguez和Lain[3]在《Science》发表的文章中提出了密度峰值聚类算法(Density Peaks Clustering,简称DPC)。相较于应用最广泛的k-means算法,该算法选取的聚类中心更加科学,而且根据密度划分可以更好地识别非球状簇,且该算法处理结果不带有随机性,结果更加稳定。

虽然DPC算法相较于k-means算法有很大的优越性,但是它依旧存在一些问题:(1)该算法的聚类中心依赖人为选取,人的主观性会影响聚类结果。(2)该算法在复杂分布的数据集中聚类效果很差[4]。本文针对DPC算法在复杂分布数据集中聚类效果不佳的问题,分析了具体问题及产生的原因并且在k近邻优化的DPC算法基础上,提出了一种连通合并优化的k近邻密度峰值聚类算法(k-nearest neighbor density peakclusteringalgorithmforconnec tedmergeoptimization,简称knn-DPCC)。本文介绍了改进算法的主要思想,主要步骤,并将该算法应用于数据集中进行验证,分类效果得以显著提升。

1 算法简介

1.1 DPC算法

DPC算法的整体思想是:聚类中心应该处于密度最大处,且各个聚类中心相距很远,聚类中心由很多同类簇数据点包围,具有很高的局部密度;不同类簇之间有明显的分界线,不同类簇的聚类中心之间相距甚远。故密度越大和与同密度等级样本点之间距离越大的数据点更具有充当聚类中心的能力。

该算法引入核函数来衡量数据所在位置的密度,核函数分为两种:高斯核(见计算公式1)和截断核[5](见计算公式2):

其中截断距离dc是所有数据点间最大距离的1%～2%(根据经验选取),d(i,j)是数据点i和数据点j之间的欧氏距离。

其中χ函数的定义如下式:

这两种定义作用相同,不同点在于:高斯核是连续函数,截断核是离散函数,在低维、数据量小的数据集中,两种定义差别不大;但是在高维或者数据量大的数据集中,采用高斯核会减小不同数据点产生相同密度值的概率,从而提高聚类准确性[6]。该算法还引入了最小距离来代表样本点i到具有更高局部密度的点j的最短欧式距离,如下式:

决策图将每个样本点以密度ρ作为横轴,参数σ作为纵轴的方式作图。往往选取决策图右上角且明显远离大部分样本的数据点作为最佳聚类中心,理想状态是存在明显处于右上角位置的样本点。右上角位置代表样本点密度较大且互相之间距离较远,通过决策图选择聚类中心的策略是DPC算法的核心。

该算法的优点确实有很多:(1)该算法不依赖数据输入的顺序,即可以打乱数据后再输入不影响聚类效果;(2)选取聚类中心的方法相对科学且聚类结果稳定,在适用范围内聚类结果可信;(3)基于密度划分的聚类算法由于采用密度排序的方式在处理非球状类簇数据时比基于距离划分的聚类算法优越性更强[7]。

1.2 k近邻密度峰值聚类

谢娟英[8]等提出了一种基于k近邻优化的密度峰值聚类算法(k-nearest neighbor density peak clustering,简称knn-DPC):定义距离数据点最近的k个点为数据的k近邻点,用数据点与k近邻点的距离来计算局部密度。这样避免了用dc这样一个全局量来衡量每个点的局部密度,相较于最初提出的DPC算法,该算法具有更大概率选取正确的聚类中心。k近邻密度峰值聚类算法是DPC算法的改进算法之一,顾名思义,该算法主要是寻找与目标样本属性最相似的k个邻居,目标样本的特征与这k个邻居紧密联系。

具体思路是:假设有数据集S={X1,X2,X3……,Xn}以及目标样本Xk。在计算完样本Xk到其余n-1个样本距离以后,对距离值进行从小到大排序,排序后前k个距离值对应的样本即目标样本Xk的k个邻居,目标样本Xk的密度计算公式[9]如下式:

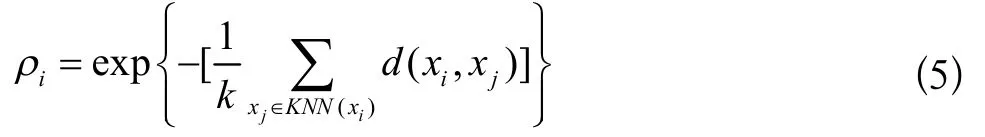
DPC算法计算了目标样本到其余所有样本的距离来并以此计算了样本处的密度,该密度是用一个全局量dc来衡量,而dc参数是一个经验参数,无法准确衡量局部密度[10],影响算法准确性。针对上述问题,knn-DPC算法的密度计算方式更能体现局部密度的特性,实践也证明了knn-DPC算法在一定程度上提升了DPC算法在密度不均匀数据集上的聚类效果。

2 连通合并优化的k近邻密度峰值聚类算法

2.1 问题分析及改进思路

虽然knn-DPC算法具有更加优良的性能,但是该算法仍然存在很大的局限性:(1)在复杂分布的数据集上准确率依然不尽人意。(2)Rodriguez和Lain认为聚类中心存在于决策图的右上角,该算法需要人为地选取聚类中心,而人们选取时会带有主观性导致聚类中心选取结果不是唯一确定的。

上述问题的出现主要有两方面原因:(1)数据集复杂程度的上升提高了聚类难度。复杂分布的数据集通常包含两个特点:密度不均匀和分布图形复杂。密度不均匀导致不同类簇间的密度值差距很大,产生一些分布相对密集的类簇,继续照搬knn-DPC算法会有很大概率在该类簇内选取多个聚类中心,即“多密度峰值”现象[11]。分布图形复杂区别于样本球型分布,球型分布直接运用欧氏距离来衡量样本间的相似度,与聚类中心距离越近的样本归属该类的概率就越大。但是在分布图形复杂的数据集中,并不能直接依靠距离远近来衡量相似程度。(2)缺少正确的聚类中心选取策略。经典DPC算法流程中需要人为选择聚类中心,马梦白等提出的(Density Peaks Clustering Analysis,简称DPCA)中聚类选取中心策略中引入了一个参数D表示标准化距离,具体计算公式见下式:

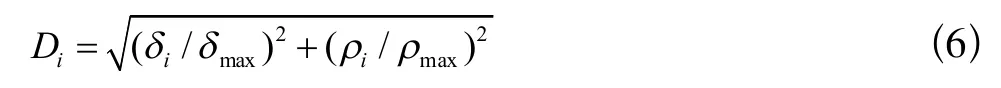
该策略认为参数D越大的点更优先成为聚类中心。上述策略是基于电能质量数据提出的,而电能质量数据具有样本数少、类别分界明显、类别数少等区别于复杂数据集的特点。继续照搬公式(6),仍然会出现“多密度峰值”现象。

为了解决上述问题,在knn-DPC算法的基础上提出新的连通合并优化的k近邻密度峰值聚类算法knn-DPCC,具体的改进思路:(1)采取连通合并的思想:将符合连通条件(见2.2节)的样本点归入相同类别;(2)引入中心影响力D的概念,对每一个样本点进行评估,中心影响力越大的点,成为聚类中心的能力越强;(3)在不考虑高维数据稀疏表示的情况下,引入相对坐标值的概念,校正坐标值的浮动范围,通过相对坐标值来完成分类工作。

2.2 连通合并优化

定义1:连通阈值e:判定两个样本点是否连通的统计量,具体判定方式:如果两个数据点间距离小于e,则称两个数据点是连通关系;如果数据点A与数据点B距离小于e且数据点A与数据点C距离大于e,而数据点B与数据点C距离小于e,那么数据点A与数据点C也成连通关系。

本文提出的结合k近邻思想进行估算相邻样本点间的最大距离,样本点的特征与周围样本点特征相近,即样本点的类别与相邻样本点类别一致。据此定义e的计算方式为所有数据点的k近邻距离中最大值乘以λ,如下式:

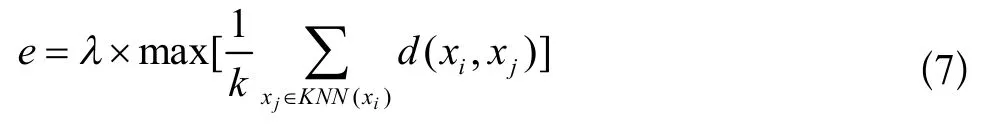
其中λ需要满足下式,Cmax为不同类簇间最小距离:

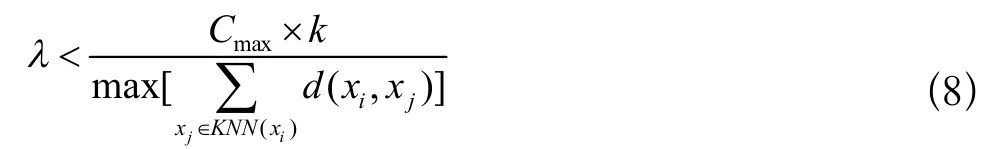
图1 算法步骤6的实现流程图Fig.1 The implementation flow chart of algorithm step 6

定义2:相对坐标值:针对横纵坐标值差距过大所做出的调整,将每个点的坐标值与x和y坐标最大值做除法,所得的两个坐标值称为相对坐标值XR、YR,取值范围均为[0,1],具体计算公式如下式:

定义3:中心影响力D:衡量一个数据点作为聚类中心的能力。按照“右上角原则”:D的值与数据点在决策图中位置息息相关,而且位于右上角的点作为聚类中心的概率更大。在新算法中定义的数据点的D越大,该点作为聚类中心的能力越强,具体计算公式如下式:

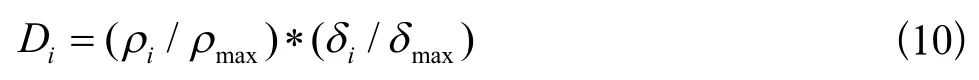
在连通阈值计算以及中心影响力计算排序完成之后,归类步骤也要做相应改进,为了避免多密度峰值问题的出现,在归类阶段首先选取一个聚类中心,搜寻所有连通的样本点,再从未归类样本点中选取下一个聚类中心,直到达到停止条件,聚类完成。

2.3 算法具体流程

Algorithm knn-DPCC

输入:数据集S={X1,X2,X3……,Xn},近邻参数k;

输出:数据集标签y={C1,C2,C3……,Cn};

Step 1.计算数据集中任意两个样本之间的距离以矩阵形式存储,并对距离矩阵的每一行进行从小到大排序,统计每个样本的k近邻距离。

Step 2.遍历所有样本,用k近邻距离计算每个样本的ρ值。

Step 3.遍历所有样本,计算每个样本的σ值。

Step 4.根据每个样本的k近邻距离计算出e参数值,计算每个点的相对坐标值XR和YR。

Step 5.根据ρi与σi值计算中心影响力Di,并完成对Di排序工作。

Step 6.按照相对坐标值归类,选出Di最大的点作为第一个聚类中心,把与第一个聚类中心连通的点全部归入第一类,并且从未归类的数据中选出下一个聚类中心,继续分类直至循环M(聚类数目)次或者数据点全部聚类完成,分类工作结束,流程图如图1所示。

3 实验与分析

为了验证knn_DPCC算法的性能,采用了不同数据集进行测试。在本次测试中分别针对本文提到的knn-DPC、DPC、DPCA三种密度峰值聚类算法与本文算法knn-DPCC进行对比测试。为了测试的公平性,knn-DPCC和knn-DPC的k近邻参数均选取10,DPC和DPCA算法中涉及的dc参数均设置为最大距离的2%。由于该四种DPC算法结果均稳定,所以只统计一次实验的数据即可。

3.1 数据集

选取两种数据集,选取Spiral、LineBlobs、Sticks、Twomoons、Aggregation五个人工数据集和Iris、Wine和Seed三组常见的UCI数据集来进行测试。人工数据集基本特性如表1所示,UCI数据集特性见表2。相比较于人工数据集,UCI数据集的分类难度更高。UCI数据集来自于现实生活,是加州大学提供的机器学习数据库,数据集多属于高维数据、类别数多且分布复杂。

3.2 算法聚类结果分析及结论

在进行数据集聚类时,为了调整四种算法输出结果易于比较,测试将类别数作为已知条件输入。为了得到较好的聚类效果,根据实际情况对新算法的λ参数进行了调整,取值为0.4。

对上述算法聚类结果统计,并采用准确率(Cluster Acurracy)和兰德指数(Rand Index)两种不同的评价标准[12]对四种DPC算法的聚类结果进行评价。两种评价标准均为已有标签据集的评价标准,四种算法的聚类效果统计结果见表3和表4,其中本文算法采用改进后的knn-DPCC算法。

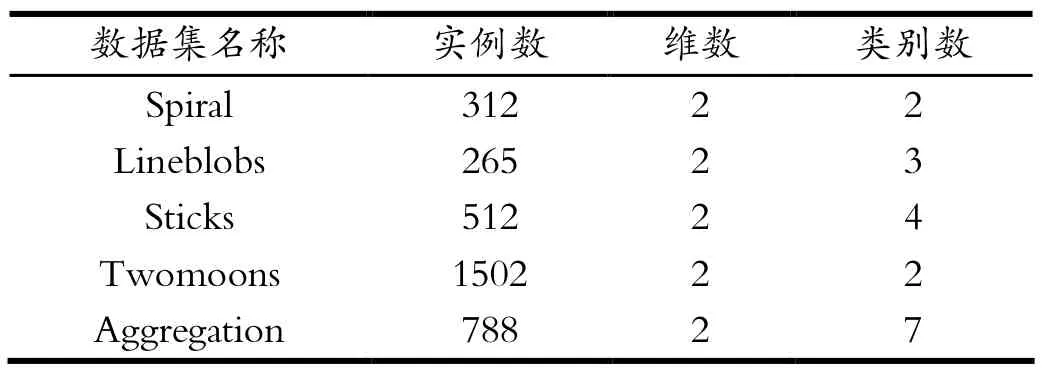
表1 人工数据集特性Tab.1 Artificial data set characteristics

表2 UCI数据集特性Tab.2 UCI data set characteristics

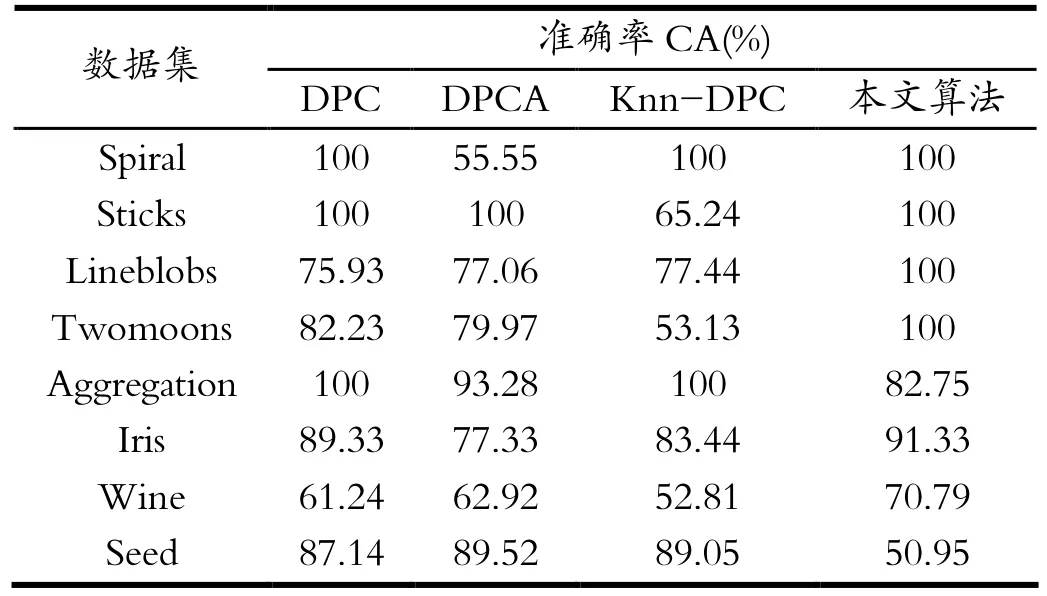
表3 算法准确性Tab.3 Algorithm accuracy

假设有数据集S={X1,X2,X3……,Xn},共有N个样本,数据集已知标签为P={Y1,Y2,Y3……Yn},聚类算法输出标签为Q={C1,C2,C3……Cn},准确率CA的计算公式如下式:

两种评价标准的取值范围均为[0,1],且完美匹配时均等于1。算法聚类效果越好,两种评价标准取值越接近1。

从上述测试结果中可以看出,DPC、DPCA和knn-DPC算法均存在较大的局限性,在多数情况下knn-DPCC算法正确率高于其他三种算法,具体表现为:(1)对于球状分布的人工数据集,是自然界中最理想也是最常见的数据集类型,特点是在数据的各个维度都服从高斯分布,就好像数据排好了队等待分类,四种聚类算法在这一类数据集上均取得了不错的效果,而且knn-DPC和knn-DPCC对于聚类中心的选取具有更高的准确性;(2)四种密度型聚类算法都受密度影响,但是knn-DPC算法受到的影响最大,原因是采用的k近邻距离计算密度,更能体现局部密度的特性;(3)当数据分布复杂时,只有knn-DPCC算法的准确性依然得以保证,DPC和DPCA算法的密度计算方式及聚类中心选取策略很大概率产生错误的聚类中心,在分类时DPC、DPCA和knn-DPC算法都容易产生归类错误,而knn-DPCC算法既汲取了局部密度的思想能够更准确地选取聚类中心,还在归类时采取了连通思想避免归类错误。在实际应用过程中按照机器学习领域的“最简单即最好”思想,应该针对不同特点的数据集选择不仅准确率高而且较为简便的算法。(4)在Aggregation数据集和Seed数据集中测试时,knn-DPCC算法聚类效果逊于其它三种算法,究其缘由,这两个数据集不同类之间有零零散散的样本点连接,不再符合类簇分明的假设。

表4 算法兰德指数Tab.4 Algorithm Rand Index

knn-DPCC算法虽然在上述数据集中应用的正确率较高,但也存在其局限性:(1)整个算法是建立在没有噪声点的前提下,所以下一步对其抗噪性能的改进需要加强;(2)整个算法有一个假设:类簇间界限分明,也是基于这个假设设置了λ(见8式)参数。如果数据集在类簇之间存在一些“雨区”,那么要根据实际情况对λ参数进行调整;再严重一些,如果数据集本身分类不明显或数据连通在一起(如Aggregation数据集),那么算法可能不再适用。针对上述问题,需要对连通合并优化的k近邻密度峰值聚类做进一步研究。

4 结语

针对经典DPC算法无法自动选取聚类中心和无法处理复杂分布以及密度不均匀分布的数据问题,本文提出了一种连通合并优化的k近邻密度峰值聚类算法(knn-DPCC),改进之后的算法不仅无需人工选择聚类中心,而且在不引入新的人为参数的前提下使新的算法在处理复杂分布和密度分布不均匀的数据时准确率有显著提升,仿真实验选取多个分布特点、维数互异的数据集并设置其他三种DPC算法作为对比实验,结果表明在新算法在处理密度不均匀以及复杂分布数据集时实现较好的聚类效果。但是在处理包含“雨区”的数据集时,无法正确分类,这也将是下一步的研究内容。因此,本文通过提出一种连通合并优化的k近邻密度峰值聚类算法,希望可以对任意形状数据类簇以及复杂情况分布的聚类相关研究及应用起到“抛砖引玉”的作用。