考虑环境传播的肺结核模型的定性分析
赵爱民,任晓晓,刘桂荣
(山西大学 数学科学学院,山西 太原 030006)
0 引言
肺结核是由结核杆菌引起的一种慢性传染病。全球每年有800万~1000万新发结核病例,其中致死病例越300万。对肺结核传播模式和传播规律进行研究具有非常重要的现实意义。肺结核具有潜伏期,潜伏时间因人而异,在潜伏期间,患者携带结核杆菌但不具有传染性。一旦患过肺结核病将终身免疫[1-3]。
预防结核病最有效的措施是接种疫苗。虽然接种疫苗会有效预防肺结核,但是接种后并不会终身免疫,只是降低了肺结核的感染率,接种者仍然具有被感染的风险。由于卡介苗免疫是活菌免疫,所以在人体内存在一段时间之后,人体内活菌减少,就会丧失免疫。考虑疫苗作用,建立肺结核传播模型,研究了无病平衡点和地方病平衡点的存在性与稳定性[4]。肺结核患者咳嗽、打喷嚏或者大声说话时,会向空气中排出携带结核杆菌的飞沫。结核杆菌生存能力很强,悬浮于空气中的结核杆菌可以存活9个小时以上,黏附在尘埃上可以保持传染性8~10天,在干燥痰中能够存活6~8个月。基于这种机理,考虑环境污染对肺结核传播模式和规律的影响,得到了平衡点的稳定性[5]。事实上,接种疫苗与环境传播在肺结核传播过程中都起着重要作用。因此,本文同时考虑接种疫苗以及环境传播,建立模型对肺结核进行研究。
1 模型建立及分析
首先,根据肺结核的发病机制[6-7],把人群分为如下几类:易感者,接种疫苗者,潜伏者(携带病菌但不具有传染性),染病者和恢复者,用S(t),V(t),E(t),I(t),R(t)分别表示t时刻易感者,接种疫苗者,潜伏者,染病者和恢复者的数量。用B(t)表示t时刻环境中结核杆菌病毒的数量。本文根据肺结核病的特点,将新生儿均考虑为易感者。人口以常数A输入,μ为自然死亡率,人与人之间的接触传染率为β,人与环境之间的传染率为α,接种疫苗率为v,疫苗影响因子为ε,免疫失效率为p,潜伏者进入染病者的转移率为δ,染病者恢复率为γ,因病死亡率为m,染病者释放到环境中病毒的速率为k,环境中病毒的失效率为τ。根据肺结核传播特点[8-9],建立疾病传播流程图,如图1所示。

图1 疾病传播流程图Fig.1 Disease transmission flow chart

2 基本再生数和平衡点的存在性
本节将给出模型(2)的平衡点的存在性及基本再生数。
令模型(2)的右端为0,容易计算得到无病平衡点P0(S0,V0,0,0,0),其中

3 平衡点的全局渐近稳定性


4 数值模拟
本节进行数值模拟,说明上述理论结果的合理性。
选取参数β=9.7×10-8,α=1.1×10-8,μ=0.0131,γ=0.09,m=0.005,v=0.9,ε=0.15,δ=26,τ=3.6,k=8,p=0.95。在图2(a)中,令A=1.7×102,进而R0≈0.00586<1。因此,模型(2)的无病平衡点是全局渐近稳定的。在图2(b)中,令A=1.7×107,进而R0≈586.25>1。因此,模型(2)存在唯一的地方病平衡点,且是全局渐近稳定的[18]。
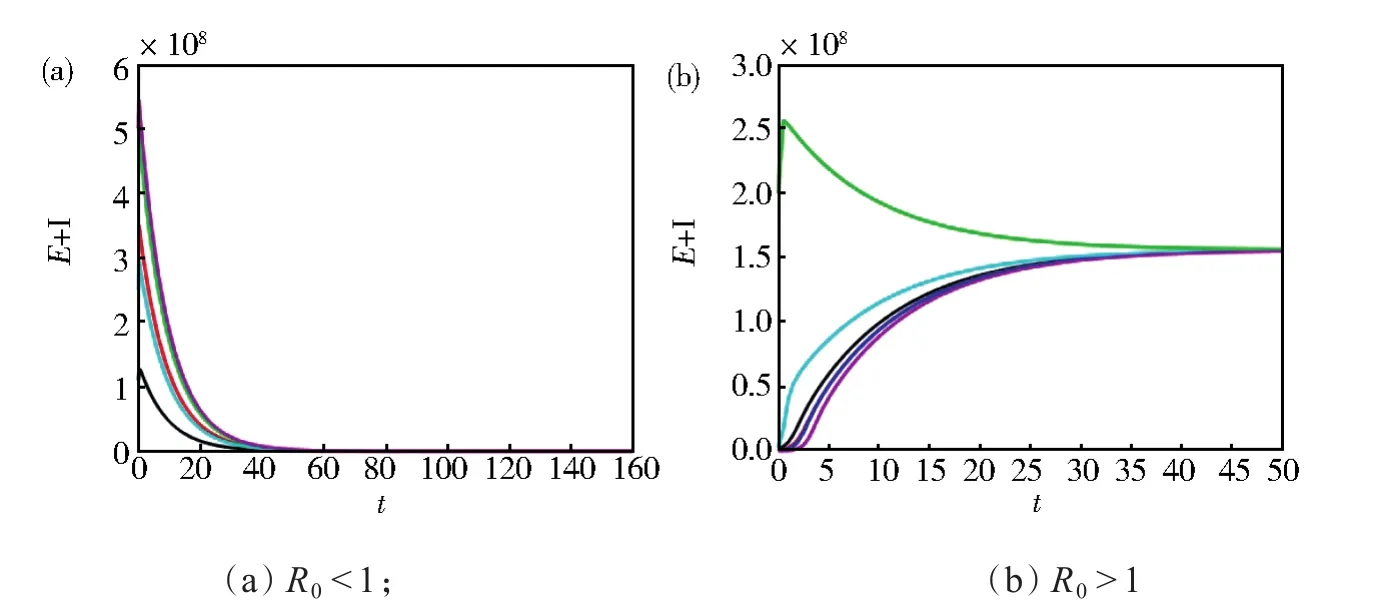
图2 E(t)+I(t)的时间序列Fig.2 Time series diagram ofE(t)+I(t)

