有心圆锥曲线的一个性质

陕西省西安市临潼区教学研究室(710600) 王江河

题目1(2017年广东揭阳一模文数第20 题.) 已知椭圆= 1(a ＞的离心率为,点M、N是椭圆C的点,且直线OM与直线ON斜率之积为

(1)求椭圆C的方程;

(2)设动点P(x0,y0)满足是否存在常数λ,使得点P是椭圆=λ上的点?

反思解题过程略,此题第二问结论是存在常数的,那么这个常数与题中那个量关系密切呢? 第二问能做一般化考虑吗? 经过笔者探求发现有心圆锥曲线一个完美的结论.

性质1已知点M、N在有心圆锥曲线C:1(m,n至少一个为正数,m·n /= 0) 上, 若点P满足当直线OM与直线ON斜率之积为定值时,则点P落在圆锥曲线上.

证明设M(x1,y1),N(x2,y2),由设点P(x0,y0), 得x0=λx1+µx2,y0=λy1+µy2, 点M、N在椭圆C:= 1 上, 所以=mn.设

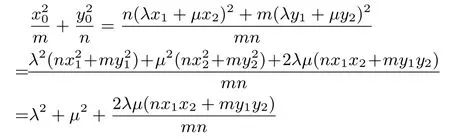
当且仅当nx1x2+my1y2=0 时,有

性质2已知点M、N在有心圆锥曲线C:1(m,n至少一个为正数,m·n /= 0) 上, 若点P满足且点P在圆锥曲线=λ2+µ2上,则直线OM与直线ON斜率之积为定值

证明设M(x1,y1),N(x2,y2), 点M、N在椭圆C:=1 上,所以设点P(x0,y0),由得

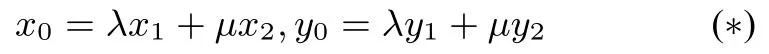
得到nx1x2+my1y2= 0.即有从而直线OM,ON斜率之积为定值

题目2已知点M、N是椭圆C:=1 上的点,设动点P(x0,y0)满足是否存在常数λ,使得点P在椭圆=λ上.

解由性质1 得存在常数λ= 5, 使得点P, 在椭圆=5 上,此时M,N满足kOM ·kON=