基于交比不变性的投影仪标定

杨建柏，赵 建 ，孙 强

（1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049）

1 引言

数字光栅投影三维测量技术作为主要的非接触测量方法，因具有精度高、分辨率高、成本低、速度快等优点，在工业检测、文物重建、逆向工程、辅助医疗等领域得到了广泛应用[1-4]。光栅投影三维测量技术是将正弦光栅图案由投影仪投射到场景中并采集相应的变形光栅图案；然后通过算法处理获取的调制光栅图像，提取相位分布；进而用已经标定好的几何关系在三维空间中重建被测物表面[5-7]。

在光栅投影三维测量过程中，系统的参数标定精度是保证测量精度的关键。相机的标定技术已经发展的很成熟[8−11]，而投影仪不能像相机那样可以找到像素点与世界坐标的准确关系，因此一直是研究的重点。为解决这一问题，研究人员提出了很多有效的方法，包括基于坐标映射的投影仪标定方法[12−15]和基于坐标变换的投影仪标定方法[16−18]。与基于坐标映射的标定方法相比较，基于坐标变换的标定方法因不需投射大量的图案，操作简单，易于计算，应用十分广泛。基于坐标变换的投影仪标定方法是将生成的带有特征点的图案投射到标定板上，采集到同时带有标定板特征和投射特征点的图像，然后提取投射特征点在图像中的坐标，再使用已标定的相机参数求得投射特征点在标定板上的位置。

然而传统的基于坐标变换的投影仪标定方法存在两个主要问题：投射到标定板上的图案会与已有的标定板图案发生干扰，影响投射特征点与板上特征点的提取；使用已标定好的相机参数计算投影仪的像素变换，产生了相机参数的误差传递，限制了标定精度。为了解决图案干扰问题，Audet[16]提出了使用二次投影的方式将特征点投射到标定板空白位置，这样便可同时采集标定板上的特征点图案和投射特征点图案。为了防止相机参数的误差传递，Anwar 等[17]提出了一种固定相机和标定板，移动投影仪进行标定的方法，从而避免了相机的标定误差转递，但是该方法无法计算系统的整体参数。高治华等[18]使用全局单应性矩阵进行坐标变换，避免了相机参数的误差传递，但全局单应性矩阵不能准确反映投影平面与标定板平面的变换关系，需要对误差使用四次函数进行拟合并补偿，计算复杂，操作不便。

为了解决上述问题，本文提出了一种新的投影仪标定方法：采用二次投影技术解决图案干扰问题；对投射特征点及周围标定板特征点进行建模，使用交比不变性计算投射特征点在标定板的位置。这种坐标变换方法未使用相机参数，避免了误差传递，有较高的精度。

2 投影仪模型

投影仪可以看作是相机的逆过程，因此，投影仪同样也可以用针孔模型以及径向和切向镜头畸变来描述[12]。如图1 所示，为了描述标定板上的特征点与相机成像平面上的像素点以及投影仪平面像素点之间的对应关系，设置3 个坐标系，包括世界坐标系OW−XWYWZW、相机坐标系Oc−XcYcZc、投影仪坐标系Op−XpYpZp。

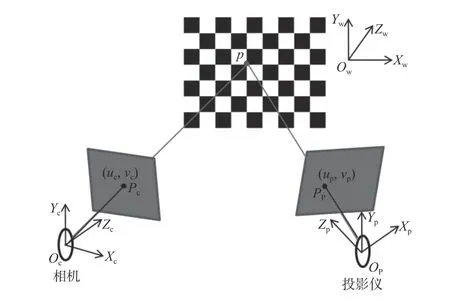
图1 测量系统简化示意图Fig.1 Schematic diagram of simplified measurement system

图1 中，P(XW,YW,ZW)表示标定板上特征点的三维坐标，Pp(up,vp)表示投影仪平面投射到该特征点的对应像素点坐标，则Pp(up,vp)与P(XW,YW,ZW)之间的关系为：

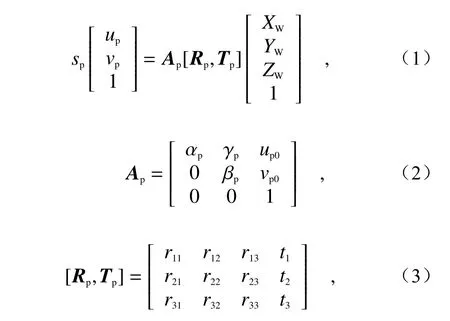
其中，sp为尺度因子，Ap为投影仪的内参矩阵，αp=fp/dup，βp=fp/dvp，fp为投影仪镜头的焦距，dup和dvp是两个坐标轴上的像素尺寸，(up0,vp0)为投影仪的主点坐标，γp为两个坐标轴的倾斜程度。Rp和Tp为投影仪的旋转矩阵和平移矩阵。如果将世界坐标系设置在标定板的表面，即Z=0，则上式可简化为：

投影仪的镜头也存在畸变，需要对其进行校正。存在畸变的情况下，理想的投影仪平面像素坐标(up,vp)和畸变后像素坐标(upd,vpd)之间的关系为：

3 投影仪标定

3.1 二次投影技术

在二次投影方法中，首先需要找到相机和标定板之间的单应性，

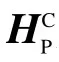
也可以写成，

图2 基于二次投影的防图案干扰方法Fig.2 Method for preventing pattern interference based on secondary projection

相对于其他防图案干扰方法，这种方法操作简单，空间利用率高，一张图即可包含两种模式的特征点，对于相应特征点的提取更加有效、准确，应用十分广泛。

3.2 交比不变性

如果忽略相机畸变，则相机成像即为标定板平面的射影变换，可以利用射影变换的性质来计算成像平面与标定板平面的变换关系。其中，交比是射影变换中最重要的不变量之一[19]。如果平面中A，B，C，D为共线的4 个点，则它们的交比可以写成：

射影变换示意图如图3 所示。

图3 射影变换示意图Fig.3 Schematic diagram of projective transformation

如图3 所示，由射影变换将直线L1上共线的4 个点a，b，c，d映射到L2上的4 个共线点A，B，C，D，则有：

在标定板平面和成像平面分别找到满足上式对应关系的共线点。使用投影仪标定算法时，最重要的便是找到标定板上特征点与投影仪图像上相应点的对应关系。在标定过程中，投影仪投射出的特征点坐标是已知的，因此如何找到特征点在标定板上的对应位置是投影仪标定能否准确的关键。在采集到的有投射特征点的标定板图像中，通过图像处理可以获得较高精度的标定板特征点的像素位置和投射特征点的像素位置。而在标定板平面坐标系中，特征点的位置已知，这样只要找到其中共线点的对应关系，即可通过射影几何中的交比不变性求得在标定板平面上投射特征点的位置，进而完成投影仪的标定。

3.3 基于交比不变性的投影仪标定方法

利用交比不变性求取投射特征点在标定板坐标系中的坐标值，首先需要构造出4 个共线点，其中包含所要求取的位置[14]。如图4 所示，AW,BW,CW,DW为标定板上相邻的4 个已知位置的标志点，EW为直线AWCW与BWDW的交点，PW为投影仪投射的特征点在标定板上的位置。使用二次投影技术时，投影特征点的位置范围基本可以确定。假设PW点位置如图4 所示，BWPW与直线AWCW交于点FW，AWPW与直线BWDW交于点GW。

图4 交比构成示意图Fig.4 Schematic diagram of cross-ratio construction

AW,BW,CW,DW通过射影变换在图像平面的对应点为AC,BC,CC,DC，如图4 所示。由于镜头存在畸变，所有连线都会有一定的失真，但是，由于AW,BW,CW,DW包围的区域较小，因此可以近似认为该区域与AC,BC,CC,DC所包围的区域为一个平面，形成没有畸变影响的射影变换。点EC，FC，GC，PC对应图中的EW，FW，GW，PW。这样，共线的两组点AW、EW、FW、CW和BW、EW、GW、DW的交比不变性可表示为：

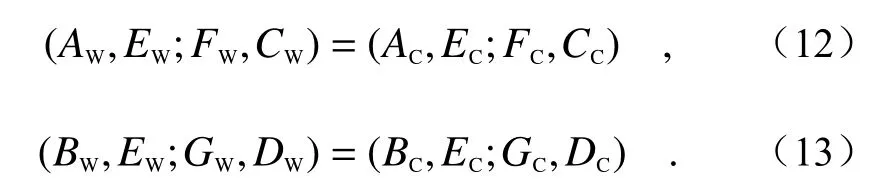
设向量a=AW，b=EW−AW，c=BW，d=EW−BW，则

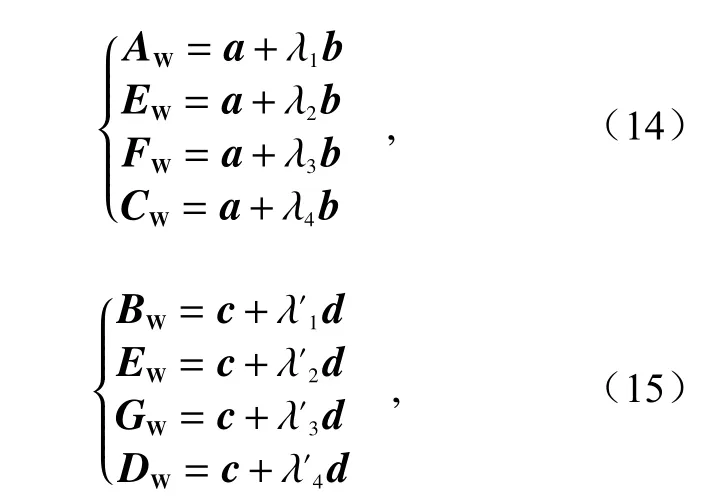
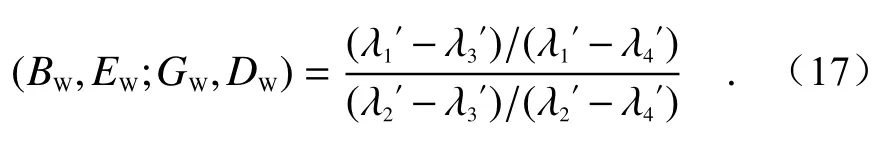
根据采集到的图像提取的特征点坐标可以求得交比(AC,EC;FC,CC)及(BC,EC;GC,DC)，也就是交比(AW,EW;FW,CW)及(BW,EW;GW,DW)的值，不妨分别设为k和k′，则可求得

由此可求得点FW，GW，即可得到直线AWGW和BWFW，它们的交点即为所要求的投射到标定板上的位置PW。这样就可以求得投影仪特征点与标定板位置之间的对应关系。再利用张正友提出的相机标定方法，即可对投影仪进行精确标定。投射特征点在标定板位置的计算是通过对相机采集图像进行特征点提取，计算出来的，因此与相机标定结果无关，不会受它的误差干扰。与全局单应性矩阵方法相比，构造交比的区域更符合射影变换的性质，因此精度更高，且整体实验不用复杂的操作即可完成，更简单准确。

4 实验过程及结果

根据上述的基于交比不变性的投影仪标定方法，标定过程可归纳为以下几个步骤：

（1）将投影仪和相机固定在实验台上，标定板放置在相机视野内，将带有已知位置十字标记的图案输入到投影仪中，并投射到标定板上，保证4 个十字图案均在标定板上呈现且十字中心尽量没有遮挡，用相机采集图像并保存。

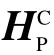
（4）将新的投影图案输入到投影仪，投射到标定板上，并用相机采集图像并保存。

（5）步骤（4）采集的二次投影图像中，投射标志点为白色圆点，将图像进行灰度翻转，使用OPENCV 中用于相机标定的函数findCirclesGrid提取出这些投射标志点在图像中的中心像素坐标，并找到其对应的邻近的标定板标志点的坐标，在标定板坐标系中找到这些标志点的位置，使用3.3 节所提出的交比不变性法计算出投射标志点在标定板坐标系中的位置。

（6）变换标定板的姿态，并重复（1）到（5）的步骤，至少需要3 种不同的姿态。

（7）用张正友相机标定方法[8]估计投影仪的内部参数和畸变系数。

为验证本文提出方法的正确性，搭建了实验系统，根据上述步骤对提出方法的有效性进行验证。图5 为搭建的实验系统图，由相机、投影仪及标定板构成。本实验所用相机为大恒水星系列MER-131-210，分辨率为1 280×1 024；投影仪为DLP6500，分辨率为1 920×1 080；标定板为白色底板，黑色圆形标志点作为特征点，这样在空白位置投射标志点，更加清晰，易于提取。投射的标志点为圆形，这样从图像中提取的标志点中心更加准确。

图5 实验系统Fig.5 Experimental system

根据上述步骤，在每个姿态下采集一幅带有投射十字标志的标定板图像，如图6 所示，本实验将标定板放置了9 个不同的姿态，选取其中3 个姿态来示意说明。

图6 第一次投影并采集的图像：（a）姿态1，（b）姿态2，（c）姿态3Fig.6 The acquired images for the first projection:(a)gesture 1,(b)gesture 2,(c)gesture 3

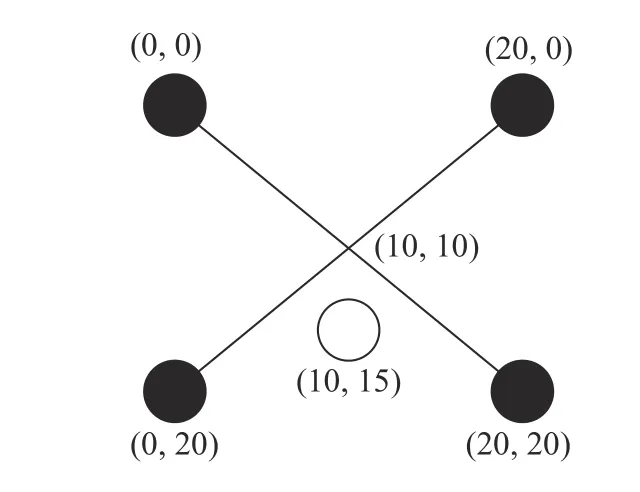
图7 投射位置示意图Fig.7 Schematic diagram of the projection position

投射位置示意图和生成的二次投影图像如图8 和图9 所示。第一次投影处理完毕，将得到的二次投影图案输入到投影仪中，投射到标定板并采集，如图10 所示。从二次采集的图像中提取出投射标志点的像素坐标，即可根据3.3 小节中的方法计算出在标定板坐标系下，投射标志点的坐标，完成标定。

图8 各姿态投射位置图：（a）姿态1，（b）姿态2，（c）姿态3Fig.8 Projection positions of each gesture:(a)gesture 1,(b)gesture 2,(c)gesture 3

图9 各姿态生成投射标志点图案：（a）姿态1，（b）姿态2，（c）姿态3Fig.9 The generated projection point patterns of each gesture:(a)gesture 1,(b)gesture 2,(c)gesture 3

图10 二次投影后采集的标定板图案：（a）姿态1，（b）姿态2，（c）姿态3Fig.10 Calibration plate patterns acquired after the second projection:(a)gesture 1,(b)gesture 2,(c)gesture 3

根据上述实验步骤，获得了较精确的标定结果。表1 和表2 列出了本方法和需要相机参数标定法以及全局单应性标定法的实验结果。

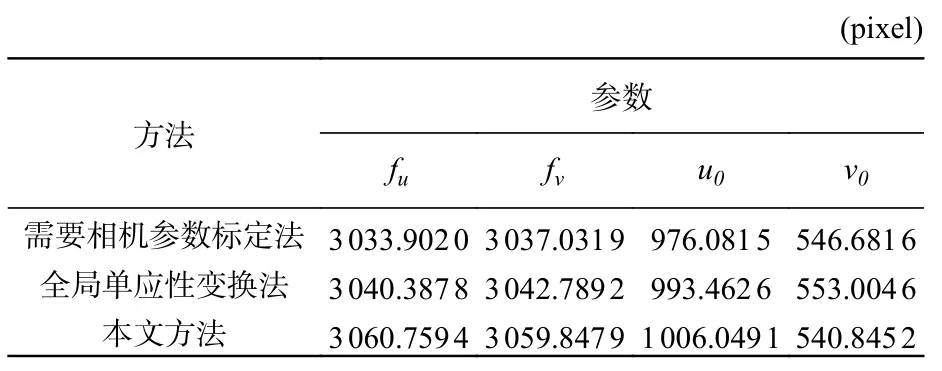
表1 标定的投影仪内部参数Tab.1 Calibrated intrinsic parameters of the projector

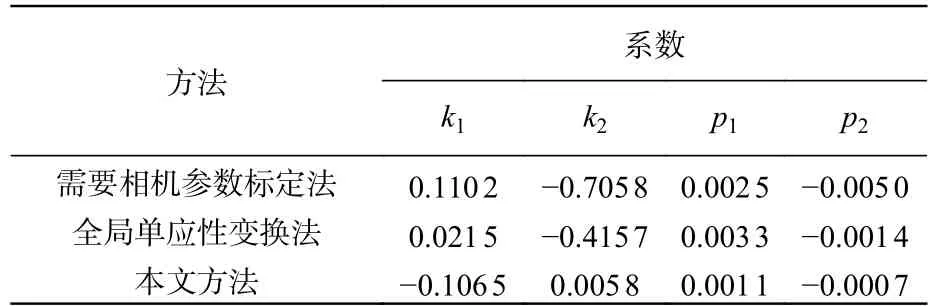
表2 标定的投影仪镜头畸变系数Tab.2 Calibrated lens distortion coefficients of the projector

为了验证该方法的有效性，对3 种方法的反投影误差进行了评估，得到的反投影误差如图11 所示。表3 列出了反投影误差在各轴上的标准差（STD）和最大值（MAX）。

从图11 和表3 可以明显看出，需要相机参数辅助计算的标定方法，因为引入了相机的标定误差，因此反投影误差最大，其标准差是（0.227 5,0.226 4）像素，误差的最大值是1.222 像素。而使用全局单应性变换的标定方法，避免了相机标定误差的传递，反投影误差有所降低，其标准差是（0.139 7,0.099 7）像素，误差的最大值是0.561 7 像素。本文提出的基于交比不变性的投影仪标定方法，采用二次投影技术解决了图案干扰问题，利用交比不变性求取投射在标定板上的特征点位置，避免了相机标定误差的引入，而且构造交比的区域更符合射影变换的性质，反投影误差最低，其标准差是（0.064 5,0.060 1）像素，其最大值是0.242 1 像素。

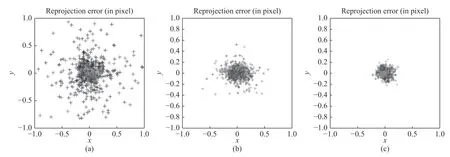
图11 几种方法的反投影误差结果。（a）需要相机参数法；（b）全局单应性变换法；（c）本文方法Fig.11 Reprojection error distribution of different methods.(a)Method requiring camera parameters;(b)the global homography transformation method;(c)the method proposed in this paper

表3 几种方法的反投影误差Tab.3 Reprojection errors of different methods(pixel)

采用本方法可以同时直接标定相机，获得整个三维测量系统的参数。相机内部参数标定结果如表4 所示。

表4 相机内部参数和畸变系数标定结果Tab.4 Calibration results of camera intrinsic parameters and distortion coefficients

相机的反投影误差的标准差在x，y两坐标轴分别为0.065 8 和0.053 9 像素，与投影仪的反投影误差的标准差在同一个量级。误差示意图如图12 所示。

同时标定相机和投影仪之后，以投影仪作为参考，可得到两设备的相对外部参数矩阵，如式（20）和式（21）所示。

得到外部参数后，结合内部参数即可获得整体测量系统的参数，从而完成系统标定。根据标定的内外参数，以投影仪作为世界坐标系原点，标定后的三维测量系统示意图如图13（彩图见期刊电子版）所示。其中左侧为投影仪，右侧为相机，不同颜色的特征点代表不同的标定板姿态。从图中可以看出相机和投影仪的空间相对位置关系，以及标定过程中每个姿态下标定板上各个特征点的世界坐标。

图12 相机标定反投影误差示意图Fig.12 Schematic diagram of reprojection error in camera calibration

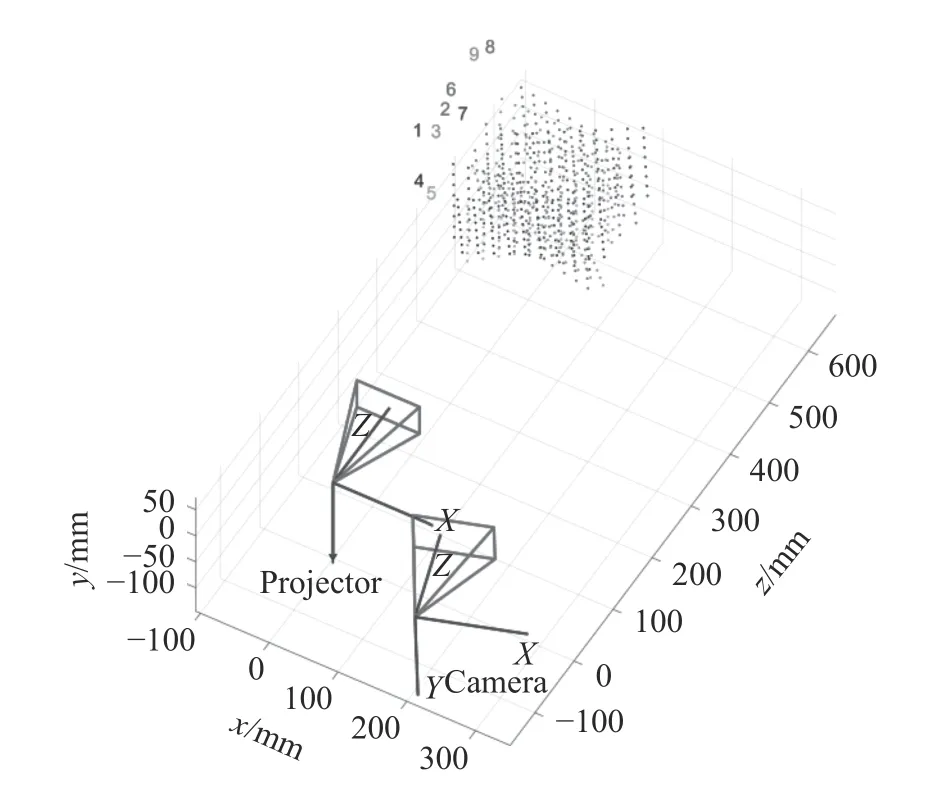
图13 整体系统三维示意图Fig.13 3 D schematic diagram of the system

5 结论

在数字光栅投影三维测量系统中，投影仪的参数标定直接影响着整个系统的测量精度。为了提高投影仪的标定精度，使用二次投影方法解决了投射图案与标定板图案的干扰问题，使用交比不变性求取标定板上投射标志点的位置，避免了相机标定参数的误差传递，并且交比的构造区域更符合射影变换的性质，因此具有更高的精度。与需要相机参数的传统标定方法以及使用全局单应性变换的标定方法进行了实验对比。结果表明，采用本方法，其反投影误差的最大值分别从1.222 像素和0.561 7 像素降到了0.242 1 像素，标准差分别从（0.227 5，0.226 4）像素和（0.139 7，0.099 7）像素降到了（0.064 5，0.060 1）像素。另外，采用本文的方法，在标定投影仪的同时可以直接标定相机，从而获得整个三维测量系统的标定参数。