多尺度奇异值分解的偏振图像融合去雾算法与实验

周文舟，范 晨，胡小平，何晓峰，张礼廉

（国防科技大学智能科学学院，湖南 长沙 410072）

1 引言

由于天气、污染等原因导致的雾霾是一种普遍现象。在雾霾天气，空气中存在很多诸如PM2.5的大气粒子，它们不仅吸收和散射场景的反射光，还会将一些大气光散射到相机，导致相机接收到的图像严重降质，能见度大大下降[1]。由于图像的质量不好，特征提取、目标跟踪以及目标识别等会受到干扰。因此，十分有必要研究图像去雾算法，以提高视觉系统的环境适应性。

随着计算机技术、光学器件技术的提高，图像去雾算法得到了广泛关注，取得了很多成果，也应用在许多领域。常见的去雾算法可以分为两类：单幅图像去雾和多幅图像去雾。Raanan Fattal[2]通过优化大气成像模型和大气衰减模型，加入了表面阴影量，从而提高了清晰度和对比度。Kaiming He[3]提出了暗通道先验算法，有效提升了算法速度以及天空区域的识别率。此外，很多学者[4−6]基于传统算法提出了改进方法，它们的基本原理都与传统算法相同。随着神经网络技术的发展，Cai B[7]基于深度学习提出一种名为DehazeNet的可训练的端到端系统，用于参数估计。该系统去雾效果相较于传统算法，色彩还原度高，清晰度高，但是其速度慢，需要前期大样本训练。

对于单幅图像去雾，使用以上方法可以有效地改善模糊图像的质量，但需要许多未知参数，因此，使用过程中通常依赖于输入图像的某些假设或先验知识[8]。多幅图像去雾算法不存在这样的问题，输入多幅图像后，可以轻松获得去雾后的图像，具备较强的去雾能力。在多幅图像去雾算法中，偏振去雾算法应用较广[8−12]。

本文针对现有偏振去雾算法鲁棒性不强和图像增强效果有限的问题，提出了一种基于多尺度奇异值分解（MSVD）的偏振图像融合去雾算法，并设计了在不同能见度条件下的验证实验。与传统偏振去雾算法相比，本文算法具有较强的自适应性和鲁棒性，能够有效改善传统算法中出现的光晕以及天空区域过曝的问题，提高了复杂光照条件下的视觉成像质量，具有较大的应用前景。

2 传统的偏振去雾算法

2.1 基于Stokes 矢量的去雾算法

在雾霾天气下，大气中悬浮大量的微小颗粒，大气光和目标反射光会与粒子发生散射。雾霾条件下相机的成像模型如图1 所示。成像系统的接收光由两部分构成：大气中的粒子对于光源(A∞)散射之后到达成像系统的大气光(A)；目标反射光强(L)经过大气中的粒子吸收和散射后的直接透射光(D)。

图1 雾霾天气下的相机成像过程Fig.1 Imaging process of camera under haze weather

未经大气散射衰减和没有大气光干扰的目标反射光强为[13]：

式（1）中总光强(I)可以由相机直接获得，通过估算无穷远处的光源A∞以及大气光A，即可计算出理想的目标反射光强，达到图像去雾的目的。

传统的偏振去雾算法通过旋转偏振片获得最亮和最暗的偏振图像，利用得到的图像进行差分，求取式(1)中的参数[8−12]。然而，这种方法是通过主观判断图像的最好与最坏，导致算法鲁棒性不强，不易操作，并且主观判断也存在较大的误差。因此，Jian Liang[12]等人提出了基于Stokes 矢量的去雾算法，首先在相机上安装偏振片，分别获得0°、45°、90°和135°的图像，Stokes 矢量可以表示为[14]：

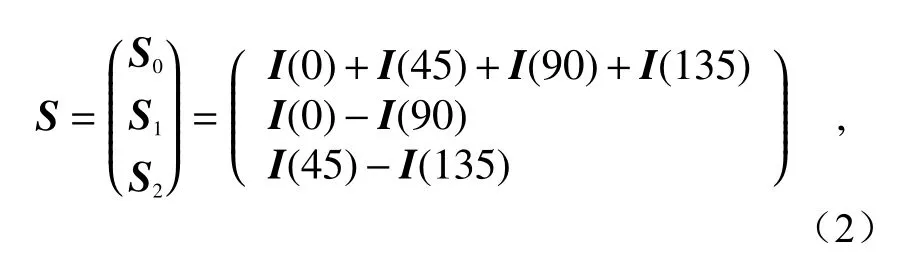
式（2）中，S0表示入射光的总强度，S1和S2表示偏振态的入射光。鉴于影响图片质量的主要为白噪声，因此通过4 幅图像相加以及2 幅图像的相减均可以达到降噪效果。偏振角(θ)计算公式为：

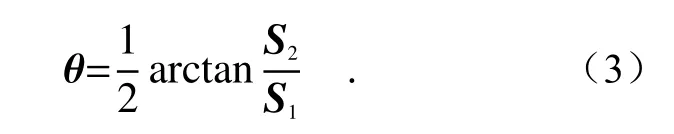
根据文献[15]，大气光可以表示为：

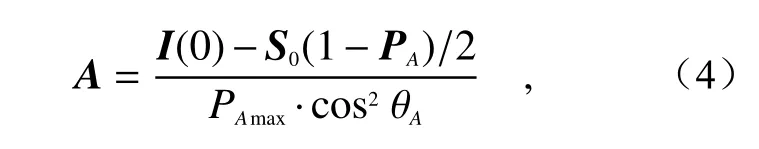
其中

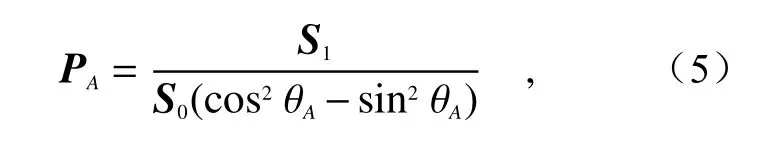
式中θA为整幅图像中出现概率最大的偏振角。

无穷远处的光源(A∞)可以通过暗通道先验方法获取[3]。暗通道图像可由式（6）获得：

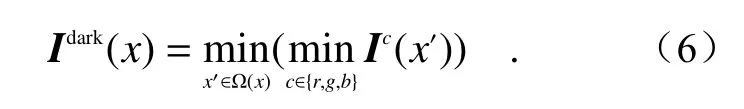
选取单个像素在红、黄、蓝3 个通道的最小值作为该像素的亮度值，然后，选择合适的窗口大小Ω(x)，在该窗口中取所有像素的最小值作为窗口所有像素的亮度值，即可得到原始图像的暗通道图像。在文献[3]中，作者根据实验经验选取窗口大小为15×15。在文献[16]中作者通过实验发现对近处物体取大窗口、对远处物体取小窗口的重构效果好，他们依据估计的深度设计了不同的窗口大小。在本文中，根据实验结果，选取窗口为15×15 进行计算。

得到暗通道图像后，选取亮度超过设定阈值的像素求平均值，得到无穷远处的光源(A∞)。将式（4）中求取A和A∞代入式（1），即可求得去雾后图像。

2.2 基于高斯滤波的去雾算法

经典的Schechner[9]算法以及2.1 节使用的方法均假设大气光是部分偏振光，直接透射光是非偏振光。但是目标反射光的偏振特性不仅与大气中的微粒有关，还与目标本身的材料、粗糙度以及颜色有关。Fang Shuai[15]拍摄了同一场景的5 000张图像，证明了目标反射光的偏振特性不可忽略，并提出了改进的雾天偏振成像模型：

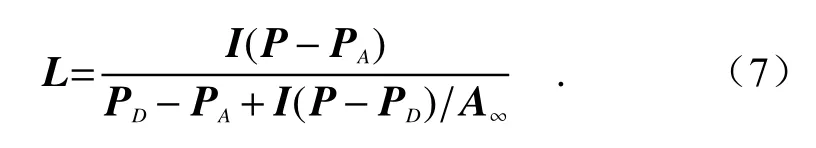
在式（7）中，总光强I和总偏振度P可以直接通过原图像计算得出。所以在该模型中，只需要估计出目标光偏振度PD，大气光偏振度PA以及无穷远处的大气光强A∞即可实现去雾。

一般大气光(A)的估算方法多是针对非偏振图像进行滤波处理，这类方法没有考虑深度对于偏振度的影响，导致距离视点较远区域重构效果较差。因此，高隽提出使用高斯滤波对大气光偏振度PA进行估计[16]。

高斯滤波是一种根据高斯分布来分配权值的线性平滑滤波器。相对于均值滤波器和中值滤波器，高斯滤波器引入了空间距离因子，对滤波窗口内的像素计算权重，位置越靠近窗口外侧的像素权重越低，其对待处理像素的影响就越小，位于窗口内侧的像素与待处理像素更接近，权重更高。高斯滤波数学表达式为：

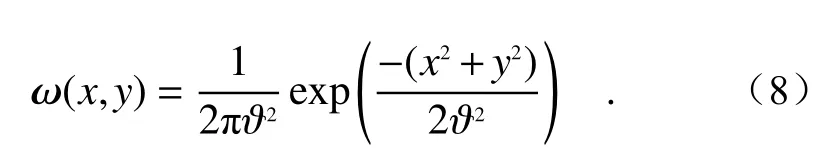
通过相机获取4 个偏振角度（0°、45°、90°、135°）下的偏振图像，对这4 幅图像进行高斯滤波处理，可得到不同偏振角度下的大气光估计图像GB(I0)、GB(I45)、GB(I90)、GB(I135)。

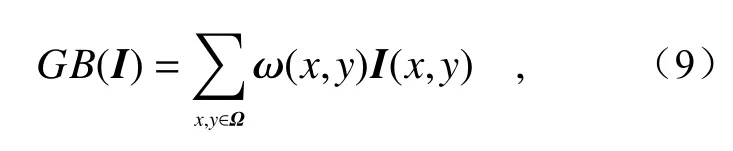
式中，ω为权重矩阵，根据去雾效果需要人工调节，x和y表示周边像素对应于中心像素坐标的相对坐标，ϑ表示模糊半径，即权重矩阵的大小；I表示待滤波图像；Ω为窗口大小，不同的图像，具有不同的最优窗口，可以根据去雾效果的要求，依据经验设定窗口大小或者手动选取窗口大小。

使用滤波处理得到的大气光估计图像计算大气光偏振度PA，由PA可求得直接透射光强(D)以及目标光偏振度PD

[15]。将求得的参数代入模型(7)中，即可得到去雾后的图像L。

3 多尺度奇异值分解的偏振图像融合去雾算法

立足于提高传统算法的适应性，提高去雾图像的质量，本文设计了如图2 所示的去雾算法流程。首先，使用基于最小二乘方法计算出更加精确的偏振信息，改善了以往偏振信息计算不准确的问题。然后，分别使用基于高斯滤波的去雾方法以及基于Stokes 矢量的去雾方法处理图像。最后，根据两种算法去雾结果的互补特性，选择计算量较小、对于高像素图像处理更简便的图像融合算法，对两种去雾结果进行融合，得到去雾效果更好的图像。

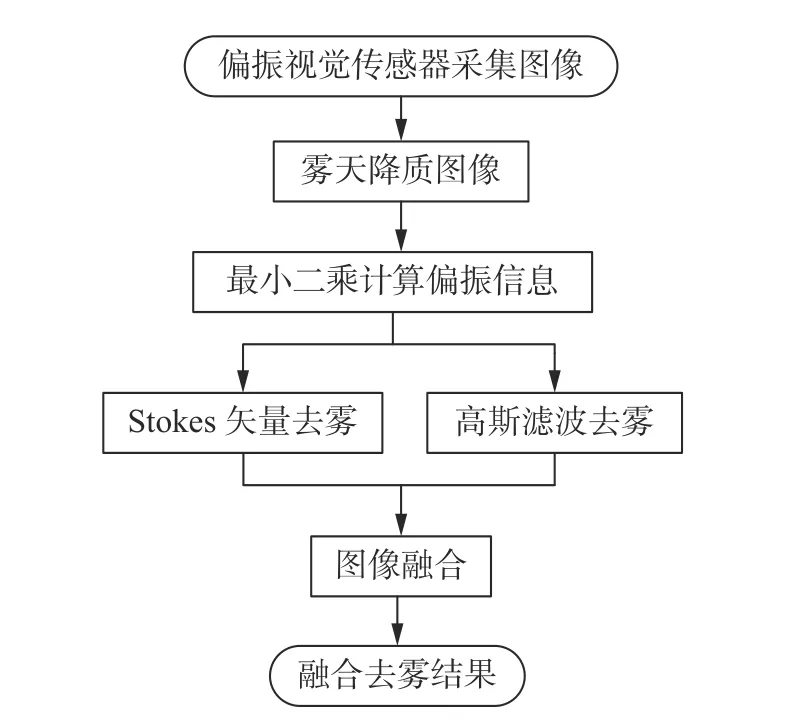
图2 多尺度奇异值分解的偏振图像融合流程图Fig.2 Flowchart of multi-scale singular value decomposition polarization image fusion

3.1 基于最小二乘的偏振信息计算

现有的偏振去雾算法本质上都是利用Stokes矢量的各分量直接求偏振角和偏振度，这种方法存在求取偏振信息噪声大、区分度不强等问题。目前可以通过偏振相机直接获得4 个方向的偏振图像，使用各个分量分别计算偏振信息并没有充分利用冗余信息。经过实验验证，基于最小二乘方法计算偏振信息较传统方法的噪声小，物体辨认更加清晰。

图3 是基于Sony IMX250 芯片的Blackfly偏振相机，相机可以通过单次曝光，对全天域偏振模式进行自动实时测量，从而获取天空的偏振信息。

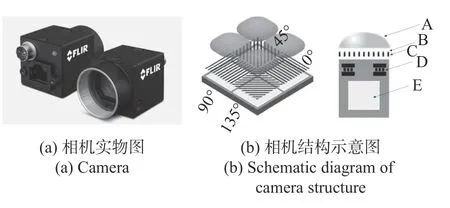
图3 Blackfly 型偏振相机Fig.3 Blackfly polarization camera

传感器具有若干偏振测量单元，如图3(b)所示，每个测量单元由4 个像素组成，对应像素具有不同的偏振敏感方向，分别为0°，45°，90°和135°，并按重复的两个像素块排列。每个像素的偏光滤镜（C）均涂有抗反射层（B），并位于镜头（A）和感光光电二极管（E）之间。

在每个像素中，忽略足够小的圆偏振光，则CCD 相机主要测量线偏振光。相机的任一像素的光强响应可以表示为[14]：

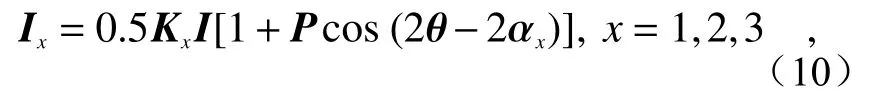
其中，Ix为像素的亮度值，Kx和 αx分 别表示相机的感光系数和雕刻光栅的极化角度，可以通过标定获得。

所求未知数共有3 个，即I、P和 θ，而Blackfly 型偏振相机可以方便地获得4 个方向的偏振图像，则重新展开可得：

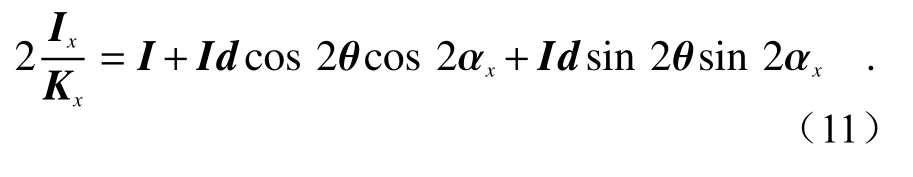
利用偏振相机得到的偏振图像联立方程，可得：

最小二乘估计为：

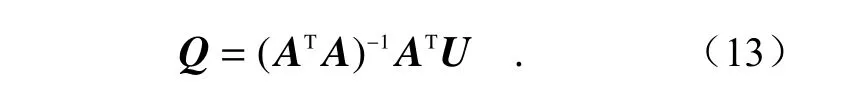
则偏振角θ 和偏振度P为：

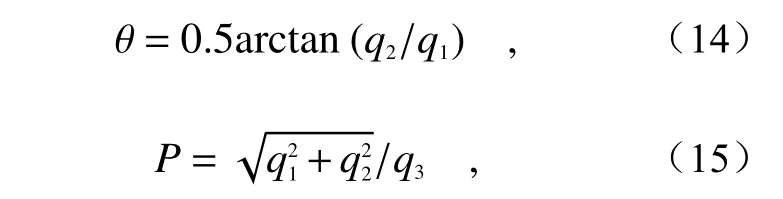
其中，q1、q2和q3为Q的向量元素。

3.2 基于多尺度奇异值分解的图像融合

图像融合可以分为像素级、特征级以及决策级融合[17]。多分辨率奇异值分解和基于小波变换的图像融合是像素级融合方法的重要构成部分。基于多分辨率奇异值分解的图像融合性能与基于小波变换的图像融合接近，但是计算更简单、实时性更好，对复杂、高像素图像处理简单方便。因此，本文使用基于多分辨率奇异值分解的图像融合。

多分辨率奇异值分解源于Burt 和Adelson 提出的拉普拉斯金字塔算法[18]，该算法类似于小波变换，基本思想是在平滑分量的每一层上用奇异值分解代替滤波。图4 展示了3 层MSVD 分解的结构。假设X是一个M×N矩阵，将X分成不重叠的2×2块，并且通过堆叠，以形成矩阵X1，并将每个块排列成4×1的向量。4×4散布矩阵的特征分解是：

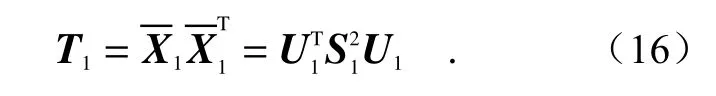
将式（16）中所得的奇异值以降序来排列：

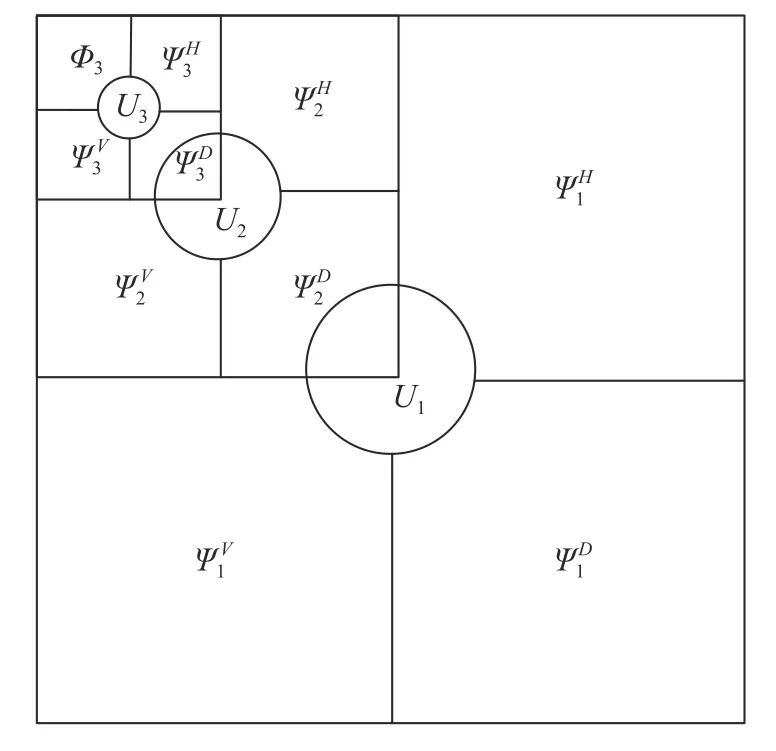
图43 层MSVD 分解结构示意图Fig.4 Schematic diagram of the three-layer MSVD decomposition structure

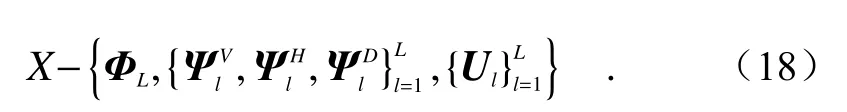
被融合的偏振去雾图像I1和I2分别用MSVD 分解为l(l=1,2,···,L)层。在每个分解层次中，细节分量系数对应于图像中更尖锐的亮度变化，如边缘图像等。而较大的奇异值能更好地保持原始低分辨率图像的有用信息，因此，将选择两个MSVD 细节分量的较大值进行融合。对于底层(l=1)，融合规则取MSVD 平滑分量系数的平均值，因为底层的平滑分量系数是原始图像的平滑和亚采样版本[17]。融合图像可通过下式得到:

4 测量实验与结果

4.1 实验装置与过程

实验整体设备和拍摄场景如图5 所示，偏振相机通过USB3.0 接口与计算机相连，使用支架固定偏振相机保持其稳定性。

图5 实验装置图Fig.5 Experimental setup

调节相机的焦距以及光圈，使相机尽可能成像清晰。通过一次曝光，即可得到偏振角度分别为0°、45°、90°以及135°的偏振图像。在不同环境条件下采集图像时，温度、气压、湿度以及能见度等均对成像有一定影响，但是能见度是决定相机成像好坏的主要因素。本文在设计实验时，主要对比了几种不同能见度条件下算法的去雾效果，以验证算法的适应性。

4.2 偏振信息计算结果

为检验改进的偏振信息计算方法效果，使用相机拍摄不同条件下的偏振图像。图6（彩图见期刊电子版）为偏振信息计算效果对比。图6(a)为晴朗无雾霾天气拍摄的图像，拍摄时能见度为30 km；图6(b)为雾霾天气拍摄图像，能见度为4 km。

图6 偏振信息计算结果示意图Fig.6 Calculation results of polarization information

由于目标的偏振特性与目标本身的材质、颜色以及光滑度有关，所以天空与建筑物、不同建筑物之间以及建筑物与树木之间的偏振信息存在差异。只要偏振信息的计算方法不存在错误，那么偏振信息的计算结果越清晰，噪声越小，则说明计算的结果越精确，误差越小。

使用3.1 节中方法计算其偏振角图像，得到偏振角和偏振度的计算结果。从图6(c)可以看出，在晴天的偏振角图像中，建筑物与天空的区分度不强，计算得出的建筑物偏振角与天空偏振角差异很小，难以区分天空以及建筑物。图像下部分建筑物的轮廓模糊不清，几乎被噪声覆盖。整幅图像的偏振角度差异不明显，噪声很大。雾天的结果与晴天的计算结果类似，建筑物的轮廓被噪声掩盖，难以区分。由此可知，传统计算方法在计算偏振角信息时引入了大量的噪声信息，存在缺陷。

图6(e)、6(f)是分别使用最小二乘方法计算的晴天偏振角度和雾天偏振角度。可见，无论是晴天还是雾天，相比于传统方法，建筑物的轮廓更加清晰，与天空的区分度也更好，引入的噪声更小。

本文使用信息熵、平均梯度以及原图与结果的相似性(SSIM)评价偏振信息计算结果，如表1、表2 所示。由表1 可知，在晴朗条件下，最小二乘法的3 项指标分别比传统方法高出14%、17%以及0.1%。因为SSIM 指标已经与1 非常接近，所以提高幅度较小，平均梯度以及信息熵两项指标均有明显的提升。

表1 晴天计算结果Tab.1 Calculation results in sunny conditions

表2 雾天计算结果Tab.2 Calculation results in foggy conditions

由表2 可知，在雾天条件下，最小二乘法的前两项指标分别比传统方法高31%、15%。从以上结果来看，无论是晴天还是雾天，最小二乘方法的绝大多数性能指标均优于传统计算方法。因此，采用最小二乘法代替传统的偏振信息计算方法，可以提高偏振信息的计算精度，降低噪声。

4.3 图像融合结果

为了验证图像融合算法的可行性，使用相机采集了不同能见度条件下的偏振图像，使用3.2节所述的算法流程处理图像。

图7（a）拍摄时能见度为3.9 km，从图中可以看到，远处的建筑物被雾霾遮挡，近处的建筑物也模糊不清，能见度大大下降，图像大部分细节丢失。

图7 图像融合去雾流程示意图Fig.7 Schematic diagram of image fusion defogging process

图7（b）是使用基于高斯滤波的去雾算法处理后的结果。在实际操作中，使用文献[16]提供的参数，并没有进行过多调节。由结果可知，去雾后整体图像的色调偏暗，图像有一些失真，建筑物的细节丢失，参数的适应性较差。但是，通过观察可以发现图像去雾有一定的效果，原本远处模糊的建筑物轮廓有所增强。

图7（c）是使用基于Stokes 矢量算法的去雾结果，相比于原图，去雾效果总体较好，远处的建筑物也能够清晰辨认，近处建筑物的细节也有所加强。但是不难发现，该图像在天空区域以及图像下方的白色雷达区域出现了过曝现象，并且建筑物边缘周围还出现了光晕现象。过曝问题通过调节模型中的参数，可以得到一定程度的改善，但是实验发现很难找到最优参数，并且过曝现象往往只能得到改善而不能完全消除。

从以上分析可知两种方法存在互补，因此，可以采用图像融合方法对两种结果加以结合。图7（d）展示了两种算法的融合结果。从图中可以发现，与基于Stokes矢量方法相比，天空区域的过度曝光现象已经消除，建筑物的光晕现象及与白色雷达的过度曝光现象有所改善。与基于高斯滤波方法相比，融合结果的图像细节更加丰富，图像更接近平时所观察到的实际场景。此外，相比于两种算法单独使用的效果，图像融合可以代替人工调节参数，从而增强了算法的鲁棒性。

为了验证算法在不同能见度下的适应性，分别在能见度为6.8 km（图8）和9 km（图9）时采集数据，并使用所提出的算法进行数据处理。

图8 能见度6.8 km 去雾结果Fig.8 Defogging results with a visibility of 6.8 km

图9 能见度9 km 去雾结果Fig.9 Defogging results with a visibility of 9 km

通过观察去雾结果可以发现，在能见度较高的情况下，相比于现有的两种算法，本文算法能在一定程度上提高了去雾效果，增加了细节信息，改善了过曝现象。在能见度较低的情况下，本文所提算法可以有效改善过曝现象，丰富图像的细节信息，显著提高图像质量，达到了去雾的效果。

为进一步验证算法的去雾效果，本文使用基于MSCNN 的开源去雾算法分别对3 种可见度的图像进行处理，结果如图10 所示。

图10 MSCNN 去雾结果Fig.10 Defogging results of MSCNN

从图10 结果来看，基于MSCNN 的去雾算法有一定的去雾效果，但是在天空区域出现了不同程度的过曝现象。几种去雾算法的信息熵以及平均梯度对比结果如表3 所示。此外，本文算法在i7-8500U 1.80GHz 计算机上使用Matlab2017b 实现，表4 中记录了4 种去雾算法处理一幅图像所需的时间。

表3 去雾效果定量比较Tab.3 Quantitative comparison of different defogging algorithms

表4 去雾时间成本定量比较Tab.4 Time-cost comparison of different defogging algorithms

在不同的天气条件下，基于Stokes 矢量方法的信息熵一般较大，这是由于基于Stokes 矢量的方法去雾效果较好，细节较为丰富，但是出现了光晕以及过曝现象，从而影响了图像的整体质量，降低了图像的平均梯度。基于MSCNN 的去雾算法有一定的去雾效果，提高了图像的信息熵以及平均梯度，但是在天空区域出现了不同程度的过曝现象。基于高斯滤波的方法在信息熵以及平均梯度上都不是最优的，但是图像没有出现光晕与过曝现象。

由表3 可知，图像融合提高了雾霾天气的信息熵，在3 种天气条件下，其信息熵较原图最大提高了1.3%，相比于高斯滤波法最大提高了18.9%。此外，无论在什么天气条件下，图像的平均梯度都得到了显著提升，相比于高斯滤波算法、Stokes矢量算法、以及MSCNN 算法最大分别提高了27.4%、38.4%和20.4%。

基于多分辨率奇异值分解的图像融合具有计算简单，对复杂、高像素图像处理更方便的优点。根据表4 各算法时间成本的对比可知，图像融合步骤的时间消耗仅为基于Stokes 矢量算法的23.3%，相比于基于滤波的算法来说，时间消耗也没有显著增加，总耗时与基于MSCNN 的去雾算法持平。综上所述，本文提出的算法在丰富图像细节、改善光晕现象的同时，没有大幅度增加整个去雾流程的计算时间。

5 结论

本文针对现有偏振去雾算法鲁棒性不强和图像增强效果有限的问题，提出了一种基于多尺度奇异值分解的偏振图像融合去雾算法。采用最小二乘法提高了偏振信息测量的准确度。在此基础上，给出了一种基于多尺度奇异值分解的偏振图像融合去雾算法，并设计实施了不同能见度条件下的验证实验。结果表明，采用本文算法进行去雾处理时图像信息熵与平均梯度最大可分别提高18.9%和38.4%，且时间成本没有大幅增加。图像融合方法具有较强的自适应性和鲁棒性，能够有效改善经典去雾算法中出现的光晕以及天空区域过曝的问题，对于利用可见光的偏振特性进行图像去雾和图像增强的效果较好，具有较强的工程实用性。总体来说，该算法有效提高了复杂光照条件下的视觉成像质量，在交通路况监控、航拍、军事目标探测与识别等视觉系统中前景广阔，具有重要的研究意义。