光学自由曲面自适应干涉检测研究新进展

张 磊，吴金灵，刘仁虎，俞本立

（安徽大学光电信息获取与控制教育部重点实验室，安徽 合肥 230601）

1 引言

光学自由曲面因具有较大的表面自由度，可以针对性地矫正像差、提高成像质量，可替代复杂传统光学元件组合使设备趋于轻量化和微型化[1-2]，因而在航空、航天、医疗、军事等行业的应用越来越广泛。近些年，随着仪器加工、新型材料合成等相关行业的发展，高质量光学自由曲面的设计[3−5]和制造[6−8]技术有了很大的进步，但其检测技术依旧没有得到很大的提升，成为了限制光学自由曲面在一些高精度光学领域应用的瓶颈。干涉检测技术因其非接触式的特点，已经在平面、球面乃至非球面检测中得到长足的发展[9−20]。然而，正是由于较大的表面自由度，使得自由曲面干涉检测技术进展缓慢，最主要的原因在于对自由曲面进行干涉检测时需要特殊设计的补偿器以补偿不同的波前像差，尤其是旋转非对称像差。很多用于旋转对称非球面干涉检测的补偿器[18−20]显得力不从心。而圆形子孔径和环形子孔径拼接方法[21−23]对非旋转对称表面也难以发挥有效作用。可见，自由曲面的非对称像差补偿在其干涉检测中至关重要，一批有价值的补偿器研究陆续开展，如计算全息图(Computer-Generated Holograms,CGH)[14,15,24,25]。理论上，设计不同的CGH 可以实现不同被测面的零位补偿，但针对不同的待测曲面，需设计不同的CGH 与之匹配，极大地影响了检测的通用化，且装调困难、费用高。尤其在自由曲面加工阶段，其面形处于持续变化中，难以获得标称面形参数，传统的静态CGH 补偿器很难适应该阶段自由曲面的原位检测。若干大动态范围的像差补偿器被陆续提出，如倾斜波干涉法(Tilted Wave Interferometer,TWI)[26]，其利用微透镜产生多个子波前，进而与相应的待测自由曲面区域进行匹配，在一定程度上增加了灵活性，但得到的干涉图复杂，且子波前携有巨大的回程误差，矫正困难，影响检测精度。此外，人们还提出了利用可变零位器[22]、可移动高次非球面单透镜[27]和双回转相位板[28]产生一定动态范围内的像差组合形式，但上述方法中补偿器件加工、检测、装调困难，且产生像差类型有限。近年来，随着自适应光学技术的发展，一批自适应光学元件开始引起了光学检测研究人员的注意，主要包括液晶空间光调制器(Liquid Crystal Spatial Light Modulator,LC-SLM)和变形镜(Deformable Mirror,DM)两大类。因具有可编程控制的自由像差调控能力，在自由曲面大动态范围像差的补偿中具有极大的潜力。自此，光学自由曲面的自适应干涉检测拉开序幕，成为目前高精度、大动态范围自由曲面检测的重要手段，尤其在自由曲面加工阶段的原位检测中可发挥重要作用。

本文梳理了近年来基于LC-SLM 和DM 的自由曲面自适应干涉检测的发展历程。结合本课题组在该领域的最新研究进展，介绍了典型自由曲面自适应干涉检测的技术要点和控制算法，对该技术现有发展瓶颈做出总分解分析并对未来发展进行了展望。

2 基于LC-SLM 的自适应干涉检测

LC-SLM 被用于CGH 的制作研究由来已久[29−31]，受此启发，2005 年Z.Cao 等人率先利用LC-SLM制作的CGH 进行光学干涉检测[32]。与传统CGH相比，基于LC-SLM 的CGH 可以动态生成而不需要在基底上制造，因此解决了CGH 在光学检测中的“唯一性”困扰。检测装置如图1 所示，使用的LC SLM 掩模的调制面积为1 cm×1 cm(32×96 像素)，检测目标为局部球面，像差校正量较小。虽然LC-SLM 相位调制精度可达λ/14(PV)和λ/100(rms)，但对凸透镜表面的实验检测精度为0.32λ(PV)和0.054λ(rms)。通过分析，像素过大是导致精度下降的主要原因。

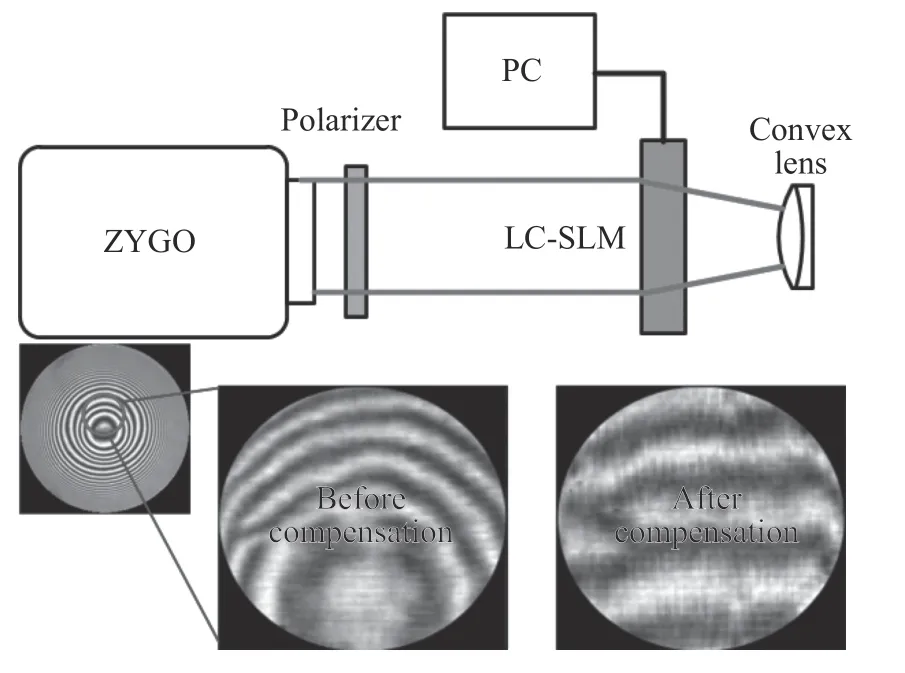
图1 基于LC-SLM 的透镜表面（球面）光学干涉检测[32]Fig.1 Interferometry of a lens surface(sphere)based on LC-SLM[32]

2006 年，Jacek Kacperski[33]等人利用反射式LC-SLM 替代了传统泰曼格林干涉仪中的标准参考镜来增加检测动态范围。所用硅基LC-SLM 的可用掩膜面积为20 mm×15 mm，像素数为1 024×768，像素大小约为19μm，256 灰度级。被测目标为1.35 mm×1.35 mm 的硅基薄膜，检测结果如图2所示。2010 年，Miguel Ares 等人[34]也利用同样方法对一块渐进多焦镜片进行了检测。

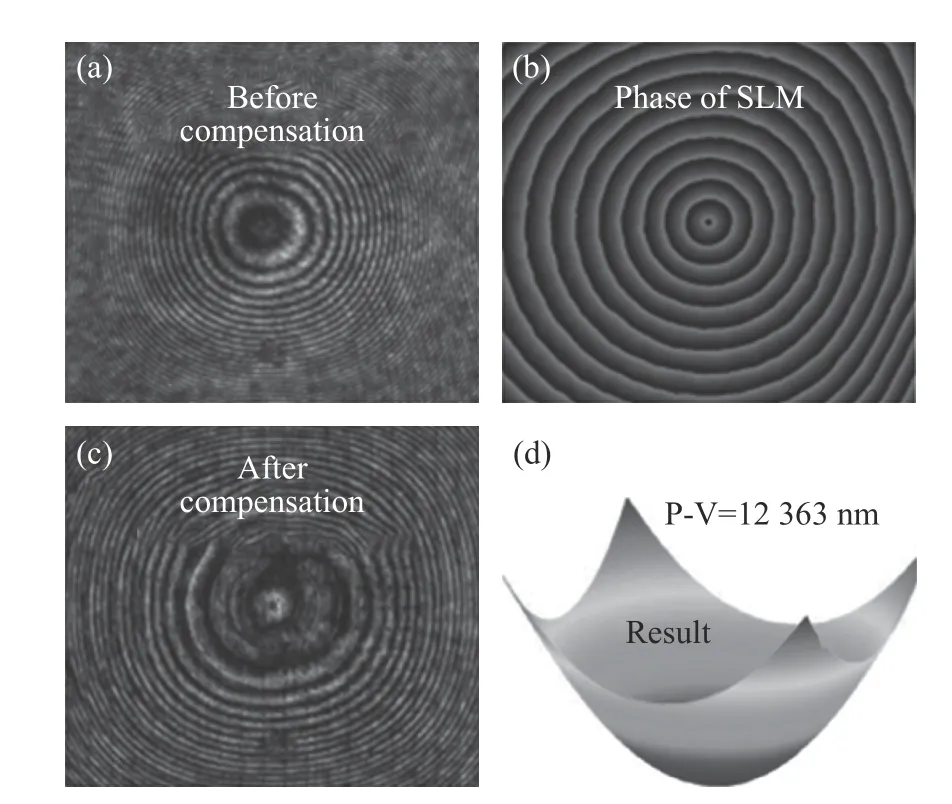
图2 LC-SLM 替代泰曼格林干涉仪的参考镜时的薄膜检测结果。（a）补偿前干涉图，（b）LC-SLM 产生的参考相位，（c）补偿后的干涉图，（d）SLM 波前调制量[33]Fig.2 Thin-film interferometry results when LC-SLM replaces the reference mirror in the Twyman-Green interferometer.(a)The pre-compensated interferogram,(b)the reference phase generated by the LCSLM,(c)the compensated interferogram,(d)the final detection result[33]

值得注意的是，Z.Cao 和Jacek Kacperski 等人的方法中，SLM 相位控制主要基于电控双折射效应，超出2π 的相位范围需要依赖解包裹技术，这种依赖相位响应（非线性）的技术具有空间、入射角和偏振敏感性。另外，0-2π 相位突变也会引入较大误差。而另一种SLM 相位控制方式是将其看作衍射光学元件[35]，2011 年，Bosanta R.Boruah等人将一种基于铁电LC-SLM 的可编程二元相位全息图应用于干涉检测中[36]，如图3 所示，二元全息图用作干涉测量的参考面产生任意波前参与干涉，并利用其横向位移实现移相；同时，采用新的随机二值化算法改善了由于高衍射级次的串扰和混叠而导致的系统精度降低。图3 所示的干涉图表明随机二值化算法在去除混叠伪影中的作用明显。但其产生的像差仅为2 rad 离焦，精度为0.045λ（rms）。2014 年，M.T.Cashmore 等人在其基础之上，证明上述方法可以在保证高精度的前提下实现较大的波前调制量（9λ（rms））[37]。

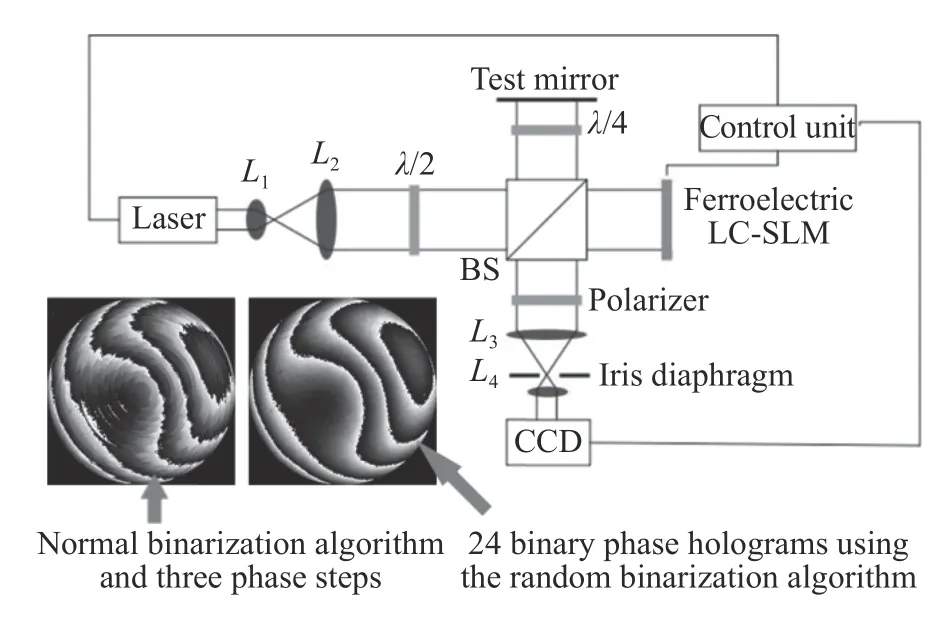
图3 基于铁基LC-SLM 的可编程二元相位全息图应用于干涉检测[36]Fig.3 A programmable binary phase hologram based on ferroelectric LC-SLM applied to interferometry[36]

2018 年，国防科技大学薛帅等人利用SLM对自由曲面实现了检测[38]，主要针对图4(a)所示的含局部大偏离度的自由曲面的检测，常规静态零位补偿器不能补偿全口径像差，导致局部干涉条纹缺失或密度超出分辨范围（图4(b)），造成图4(c)所示部分区域面形数据缺失。利用可编程SLM 可实现局部区域零位检测（图4(d)−4(g)），进而进行全口径拼接（4(h)）。文中采用1 024×768像素的SLM，可补偿26 mm 口径内约40μm 像差（对应偏离度约为20μm），自适应补偿效果如图5 所示。

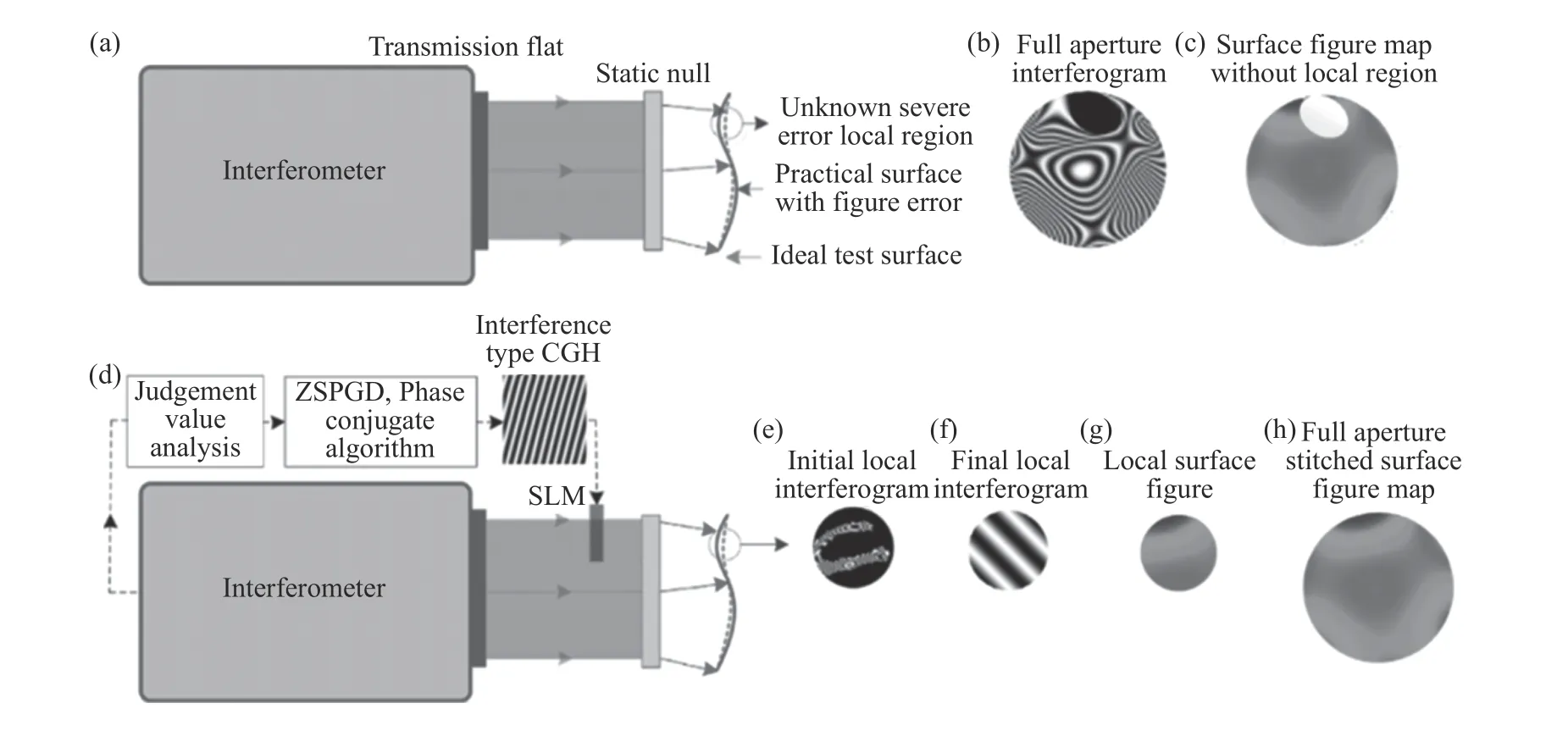
图4 基于SLM 的自适应波前干涉仪对大面形误差自由曲面检测示意图。（a）利用静态零位镜对自由曲面进行的常规检测；（b）全孔径干涉图中部分条纹不能分辨；（c）表面面形误差分布具有部分数据缺失；（d）基于SLM 的自由曲面检测；（e）局部区域的初始不能分辨干涉图；（f）被SLM 补偿的局部区域的最终干涉图；（g）局部区域的曲面面形误差；（h）全孔径曲面面形误差图拼接结果[38]Fig.4 Illustration of the SLM-based Adaptive Wave-front Interferometer(AWI)for freeform surfaces with severe surface figure error.(a)The conventional test of a freeform surface utilizing a static null.(b)The full aperture interferogram when the upper region cannot be resolved by the interferometer.(c)The surface figure error map when the upper region is not available.(d)The SLM-based AWI.(e)The initial interferogram of the local region.(f)The final interferogram of the local region nulled by the SLM.(g)The surface figure error of the local region.(h)The full aperture surface figure error map stitching result[38]

图5 自适应补偿过程中检测干涉条纹密度变化[38]Fig.5 The variation in interferogram density during adaptive compensation[38]

针对前述的SLM 相位控制难点，2019 年薛帅等人又研究了利用LC-SLM 作为可重构的多级干涉型计算全息图产生对非球面和自由曲面进行全口径动态零位检测的方法[39]，分别研究了如图6(a)和6(b)所示的准直和汇聚光路中LC-SLM的控制，并分别完成了约30λ（λ=632.8 nm，约19μm）偏离度的φ 多项式曲面和约27λ（17μm）偏离度的双圆锥曲面检测，并将检测结果分别与Lupho-Scan 260 扫描干涉仪检测结果和非零位检测结果进行了比对，精度均为rms 0.039λ。

随后，薛帅等人[40]又报道了利用可移动非球面零位镜（Refractive Aspheric Null Lens,RANL）与LC-SLM 组合补偿器，如图7（a）（彩图见期刊电子版）所示。通过非球面零位镜的沿轴平移和可编程控制LC-SLM可实现动态像差调制，图中LenScan LS600 用来实现RANL 的定位。通过上述补偿结构，可实现最大230λ的旋转对称像差和40λ的非旋转对称像差补偿，RANL 与LC-SLM各自的像差调控能力如图7(b)（彩图见期刊电子版）所示。实验检测了对于最佳适配球约183λPV偏离度的双圆锥面，其中非旋转对称组分约23.786λPV。与LuphoScan 扫描干涉仪检测结果相比，rms 精度约0.036λ。

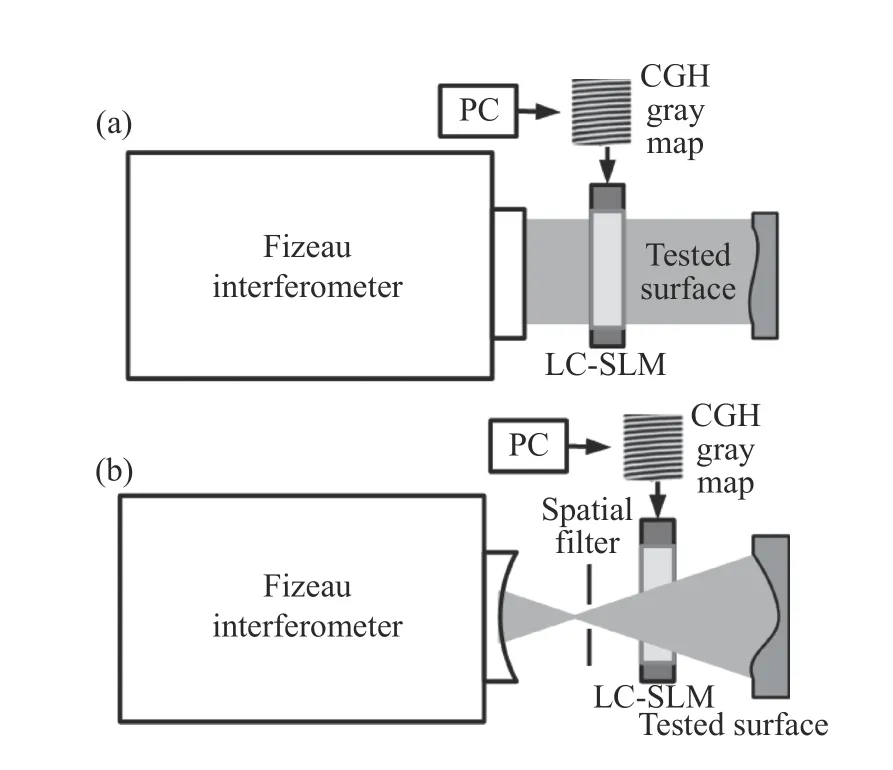
图6 利用LC-SLM 作为可重构的多级干涉型计算全图产生对自由曲面进行全口径零位检测。（a）准直光入射，（b）汇聚（发散）光入射[39]Fig.6 LC-SLM is used as a reconfigurable multistage interferometric CGH to perform a full-aperture null test on the freeform surface,with(a)the collimating light incident and(b)the converging(divergent)light incident[39]

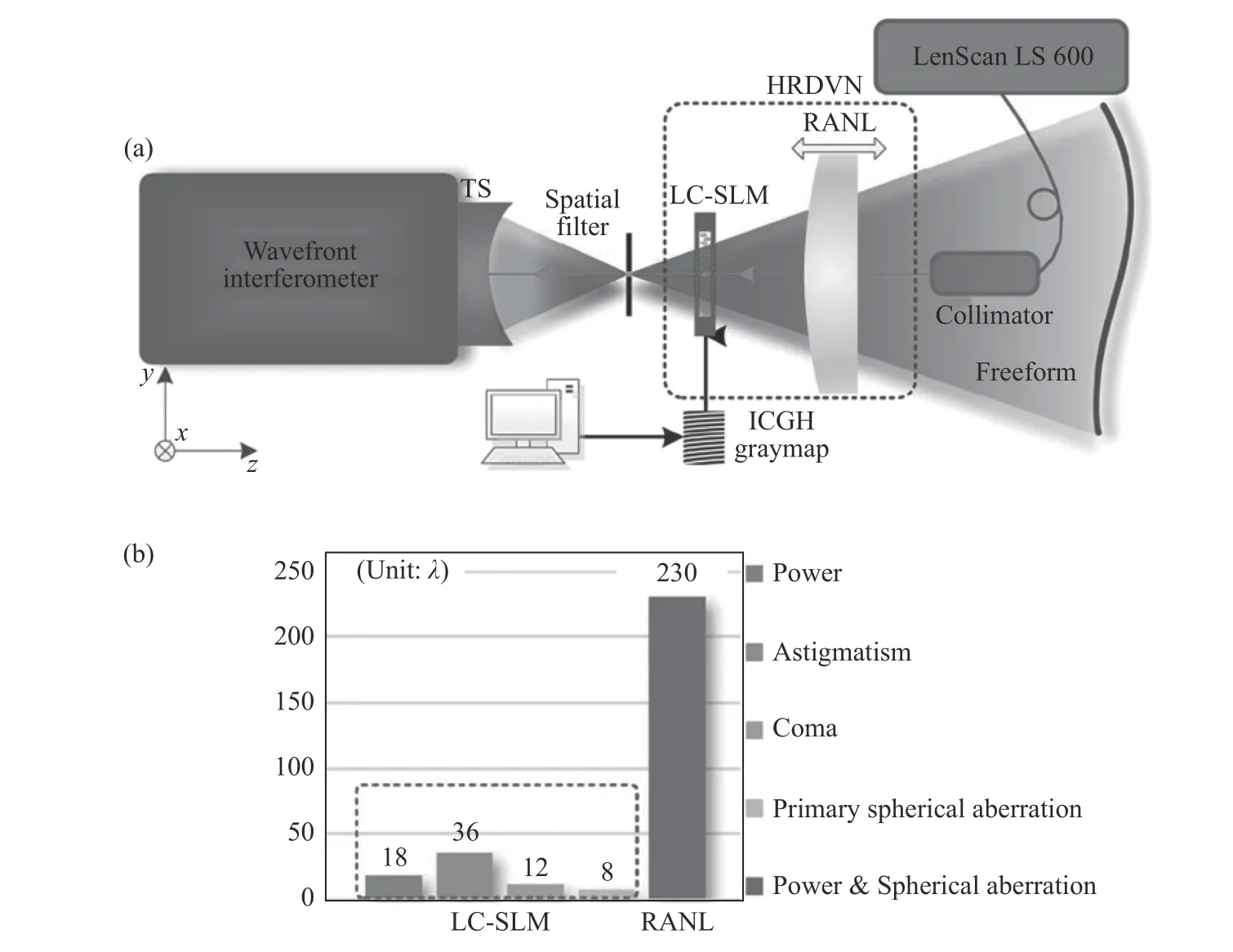
图7 利用可移动非球面零位镜与LC-SLM 组合补偿器实现自由曲面大动态范围零位检测[40]Fig.7 Schematic layout of the flexible null metrology system for freeform surfaces using a Refractive Aspheric Null Lens(RANL)and a LC-SLM[40]

目前实验报道的SLM 自适应干涉仪对于非旋转对称像差补偿的动态范围最大约20μm，Romita Chaudhuri 设计了一种基于高清纯相位反射式SLM 的自由曲面干涉检测结构[41]，如图8（彩图见期刊电子版）所示，该结构采用了先进的SLM[42]（4 160×2 464 像素的Holoeye GAEA2)，能够产生数百微米PV 的波前调制量。通过对该SLM 的建模，证明其能检测的自由曲面偏离度高达150μm（口径4 英寸），由SLM 的像素化和相位量化引起的面形测量的理论不确定度为50.62 nm rms。但该检测方法目前仅实现于计算机仿真，其实际实验将在不久的将来进行报道。

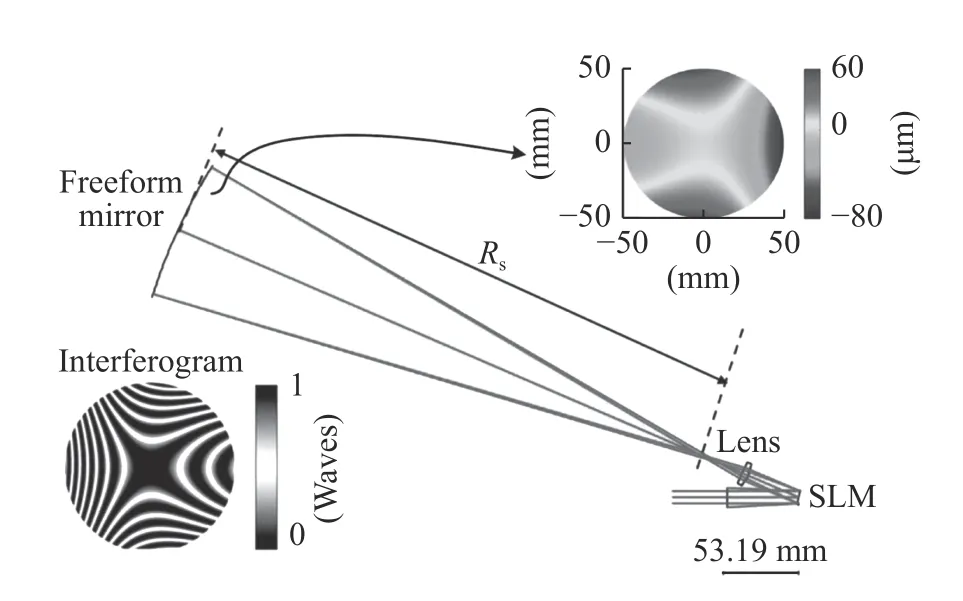
图8 基于大调制量的SLM 的零位检测结构Fig.8 The null test layout in the optical design with the SLM

3 基于DM 的自适应干涉检测技术

自DM 面世以来便在波前校正领域备受关注，已被广泛应用于大气光学[43-44]，眼科学[45-46]等领域。2004 年,C.Pruss[47]等人利用薄膜DM 进行了非球面干涉检测的研究，其干涉检测装置如图9(a)所示。他们采用薄膜DM 实现了大动态范围的离焦和球差补偿，最终通过对系统的光线追迹得到被测非球面面形（面形误差）。其采用的薄膜DM 口径为25 mm，最大波前调制达40μm PV，重复精度为50 nm。作为动态的自适应补偿器，DM 的形变量和形变精度是首要考虑的因素。文献[47]中指出薄膜DM 的形变量主要取决于膜的材料常数与应力特性、驱动电极与膜层的间隙以及驱动电压。图9(b)给出了驱动电压与DM 反射波前PV 的模型预测值和实际测量值之间的关系。图9(c)展示了不同驱动电压下DM全口径形变量（截面）。因被测面为旋转对称非球面，这里主要考察了旋转对称形变。

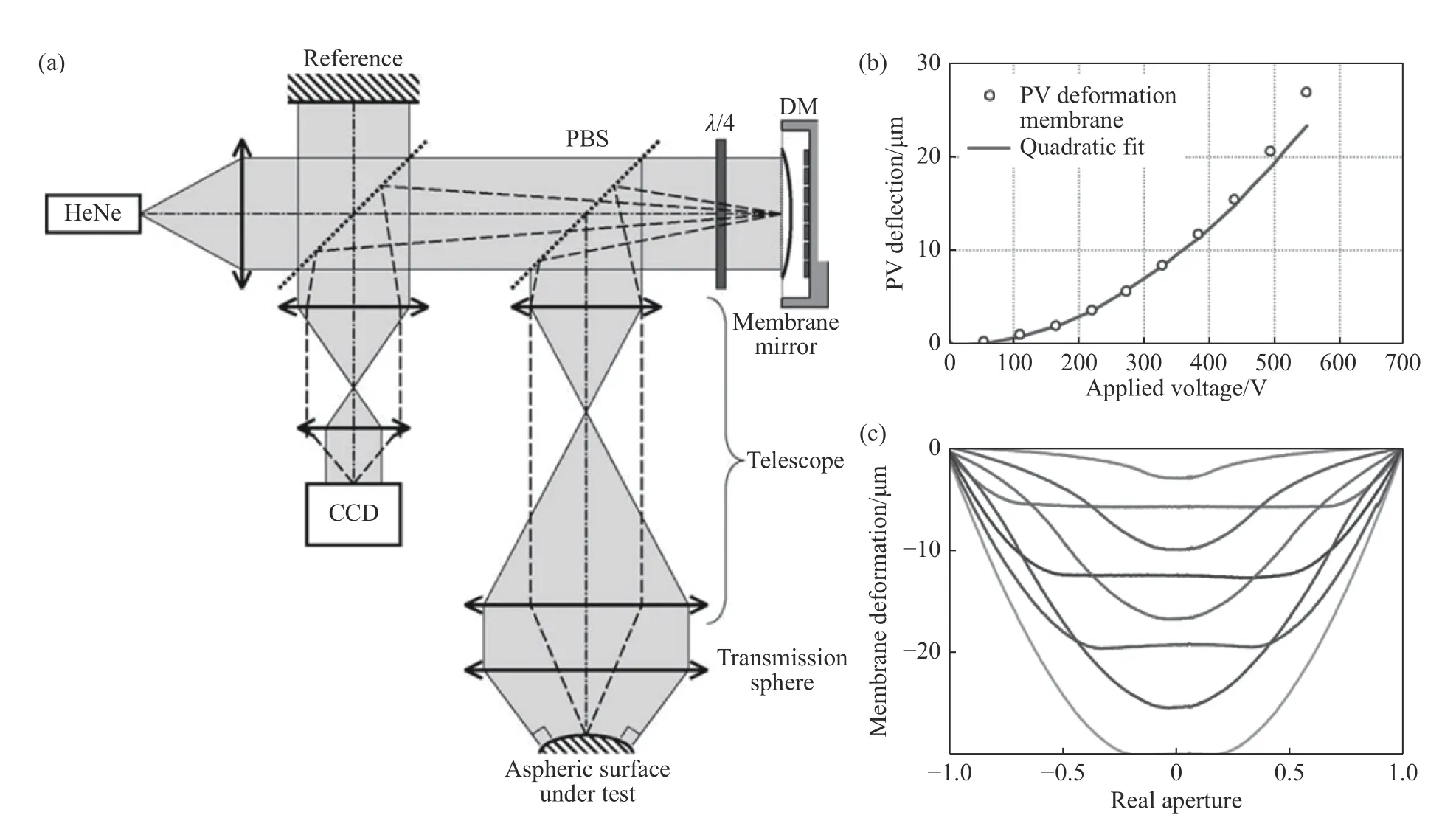
图9 基于薄膜DM 的非球面动态干涉检测。（a）干涉检测系统布局；（b）驱动电压与DM 反射波前PV 的模型预测值和实际测量值之间的关系；（c）不同驱动电压下DM 全口径形变量（截面）[47]Fig.9 Aspheric dynamic interferometer based on a thin film DM.(a)Layout of the system;(b)the relationship between the model predicted value and the actual measured value for PV of the DM-reflected wavefront with applied voltage and(c)the DM’s full aperture shapes(section)under different driving voltages[47]

值得注意的是，最终被测面形是采用基于光线追迹的方法求取的，系统参数的建模精度尤为重要。作为补偿器的DM 的精度则是重中之重。而处于工作状态的DM 表面也是自由曲面，且该曲面表面形变精度与其驱动器的整体驱动电压矩阵关系是非线性的[48]。虽然很多商业化DM已经集成了Zernike 系数控制矩阵模块，以方便实验人员直接调用表面Zernike 控制命令，但由于驱动器间的交连影响，表面形变反射波前依然与给定的Zernike 系数表征波前存在差异；同时，由于环境因素的影响，DM 表面可能随时间和温度发生蠕变，从而影响整体检测精度。C.Pruss 等人在上述检测中利用旋转或者撤出1/4 波片的方式实现DM 表面的原位检测，但在一定程度上影响了实时性。

可见，在自由曲面干涉检测中，对DM 表面形变精确监测和建模是整个检测过程中必不可少的一部分。2014 年，Fuerschbach 等人[49]在DM的辅助下利用特殊设计的离轴结构对一个φ 多项式反射镜进行了零位检测。其检测原理如图10（a）所示，但在该检测中被测φ 多项式反射镜的标称面形方程已知，可以分解为多个Zernike组分：球差、像散、彗差以及高阶像差。针对这些Zernike 像差组分，系统设计以Offner 补偿器[18]、离轴光路以及DM 进行组合式补偿。由于被测面标称面形方程已知，所需DM 形变由图10（b）所示的结构提前产生，采用经典的自适应光学反馈控制结构，利用波前传感器提供Zernike 系数反馈，使DM 产生所需的形变量（约11μm PV），同时采用Zygo 干涉仪精确测量所产生的实际形变。可见，该方法中针对DM 表面的检测是在图10（b）的结构中提前完成的，再利用已发生形变的DM构建图10（a）所示离轴结构，因此不适合原位测量，且实时性大打折扣。

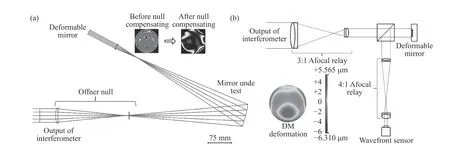
图10 利用DM 配合Offner 补偿器进行φ 多项式反射镜检测。（a）系统布局；（b）DM 形变产生及测量系统[49]Fig.10 Test of aφpolynomial reflector with a DM and an Offner compensator.(a)System layout;(b)DM deformation generation and measurement system[49]

2016 年，黄磊[50]提出了一种测量未知自由曲面的自适应零位干涉检测方法。如图11 所示，该方法利用DM 辅助静态零位补偿器实现自由曲面未知面形测量，同时采用相位偏折测量系统(Deflectometry system,DS)[51-52]实时原位监测DM表面的面形。最终通过系统模型光线追迹求得被测面面形。由于被测标称面形未知，DM 的补偿量难以直接获得，因此采用随机并行梯度下降(Stochastic Parallel Gradient Descent，SPGD)算法[53-54]进行DM 形变优化，以稀疏干涉条纹为最终优化目标。实验中采用的变形镜为ALPAO DM52-25（口径15 mm，驱动器数量52），最终测得自由曲面的平面偏离度为15.79μm。虽然该方法有效地实施了自由曲面原位测量，但用来实时监测DM 形变的高精度的DS 标定复杂[51]，且不利于干涉系统集成。

图11 测量未知自由曲面的自适应零位干涉检测方法[50]Fig.11 Schematic of adaptive metrology system layout[50]

2018 年，安徽大学张磊等人提出了一种用于光学自由曲面检测的自适应干涉仪[55]，同样利用DM 和部分补偿器(Partial Null Optics,PNO)[11,20]组成自适应零位补偿器（Adaptive Null Compensator,ANC）补偿被测自由曲面的非旋转对称与旋转对称像差。该方法利用偏振设计实现了被测自由曲面和DM 表面的原位实时干涉检测，即在同一干涉仪上实现了DM 表面的实时监测和自由曲面检测。检测系统如图12（a）（彩图见期刊电子版）所示，通过双CCD 同时接收自由曲面测量干涉图与DM 监测干涉图，系统偏振设计如图12（b）（彩图见期刊电子版）所示。系统中采用ALPAO 公司的DM88-25，可实现最大40μm 的波前调制量（PV），系统中波前经过两次DM 反射可实现80μm波前调制。但该系统检测光路较为复杂，需要两个CCD 同时进行工作，不能与一般商用干涉仪（如ZYGO 干涉仪）配合使用，不利于自由曲面光学元件车间检验的发展。针对这一问题，采用波前传感器（WaveFront Sensor，WFS）替代干涉仪内部的一台CCD 设备，在干涉系统外部实时监测DM 形变，如图13 所示[56]。由于波前传感器可作为干涉仪的外置辅助设备，因此可配合商业干涉仪实现自由曲面光学元件车间检验。

单个DM 的动态范围有限，利用双DM 级联可有效增加动态范围，该方法已被用于多个领域[57−60]。2019 年，为进一步扩大自由曲面检测动态范围，张磊等人[61]继续提出双DM 级联的方式进行未知自由曲面自适应检测。如图14（a）（彩图见期刊电子版）所示，利用双DM 级联的方式（woofer DM 和tweeter DM），将自由曲面非旋转对称偏离检测动态范围增大一倍，一般来说，woofer DM 有相对较大的冲程，适合于低阶像差补偿，而tweeter DM 有高驱动器密度，因此适合高分辨率的高阶像差校正。配合两片可调波片(Tunable Wave Plate，TWP)和补偿旋转对称像差的PNO 组成混合补偿系统（Hybrid Compensating System，HCS)，HCS 的具体偏振光束传播设计如图14(b)（彩图见期刊电子版）所示。结果表明，HCS 不会改变透射光束的偏振方向。文中采用典型的商用DMs，如ALPAO DMs，能够提供30～40μm 的像差校正量，它可以通过级联两个DMs 提供60～80μm 的校正量。值得注意的是，光束通过HCS 两次，因此获得的最大像差覆盖范围约160μm，即最大可测80μm 的旋转非对称偏离度。对于级联DM的补偿系统，主要面临两个问题：（1）双DM 形变监测；（2）双DM 像差耦合[58,60]矫正。由于两个DM 需要分别监测，系统通过分别转动两片TWP的方式对双DM 进行时分监测，同时，为DM 控制器配备了高稳定性模块[62-63]，减小非实时监测的影响，其开环稳定性在一小时内可达几纳米rms。通常woofer DM 和tweeter DM 分别用于提供低阶和高阶像差补偿，但并不总是这样。事实上，双DM 可能出现补偿耦合，导致无谓的波前校正浪费。如果不能有效地抑制耦合，随着闭环时间的增加，DM 冲程容积将完全被累积的耦合消耗掉。同时双DM 的最终形变校正量应保持平均化，以免其中一个DM 产生过大负载，导致形变无法监测。该系统采用基于SPGD 的解耦平均算法实现双DM 解耦和平均化形变[61]。

图12 光学自由曲面检测的自适应偏振干涉仪[55]。（a）系统布局；（b）系统偏振设计Fig.12 Adaptive polarization interferometer for optical freeform surface metrology[55].(a)System layout;(b)polarization design

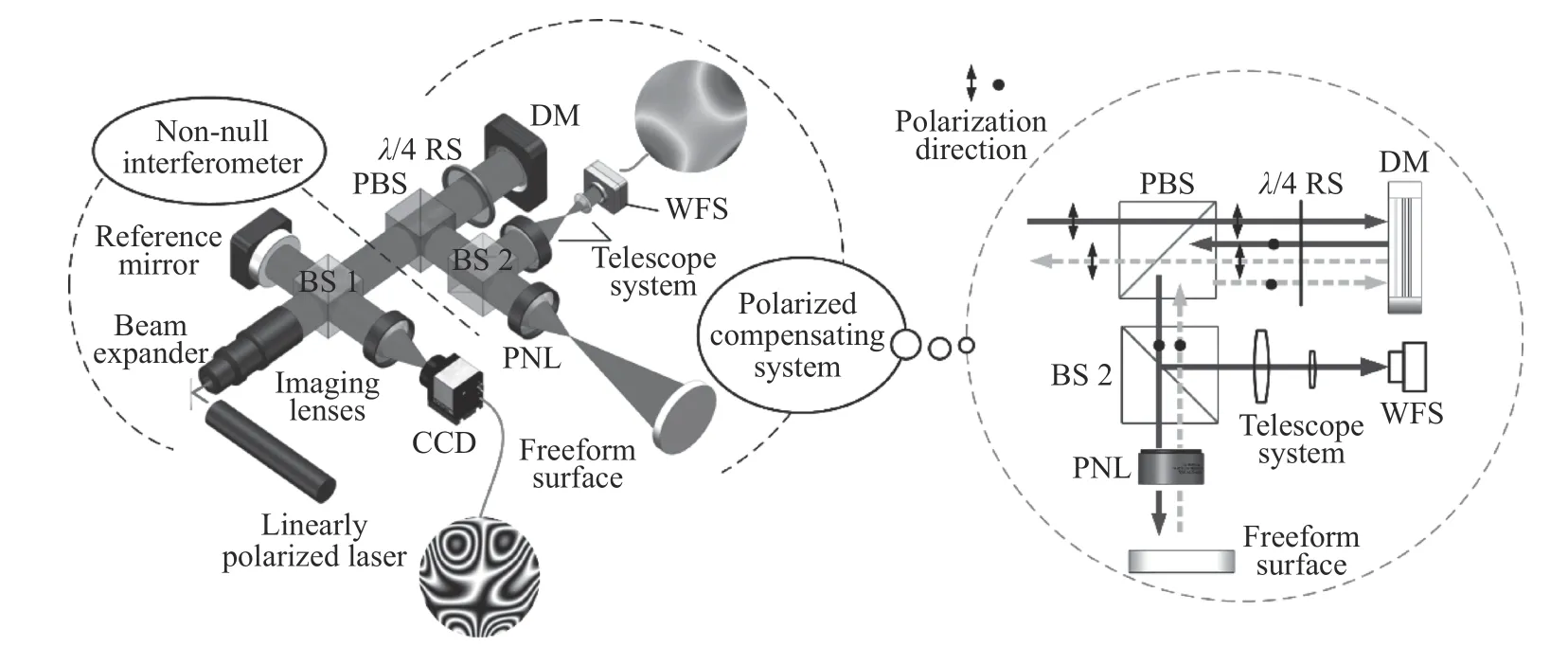
图13 可配合商用干涉仪的光学自由曲面自适应偏振干涉仪[56]Fig.13 The optical freeform surface adaptive polarization interferometer that can cooperate with commercial interferometers[56]

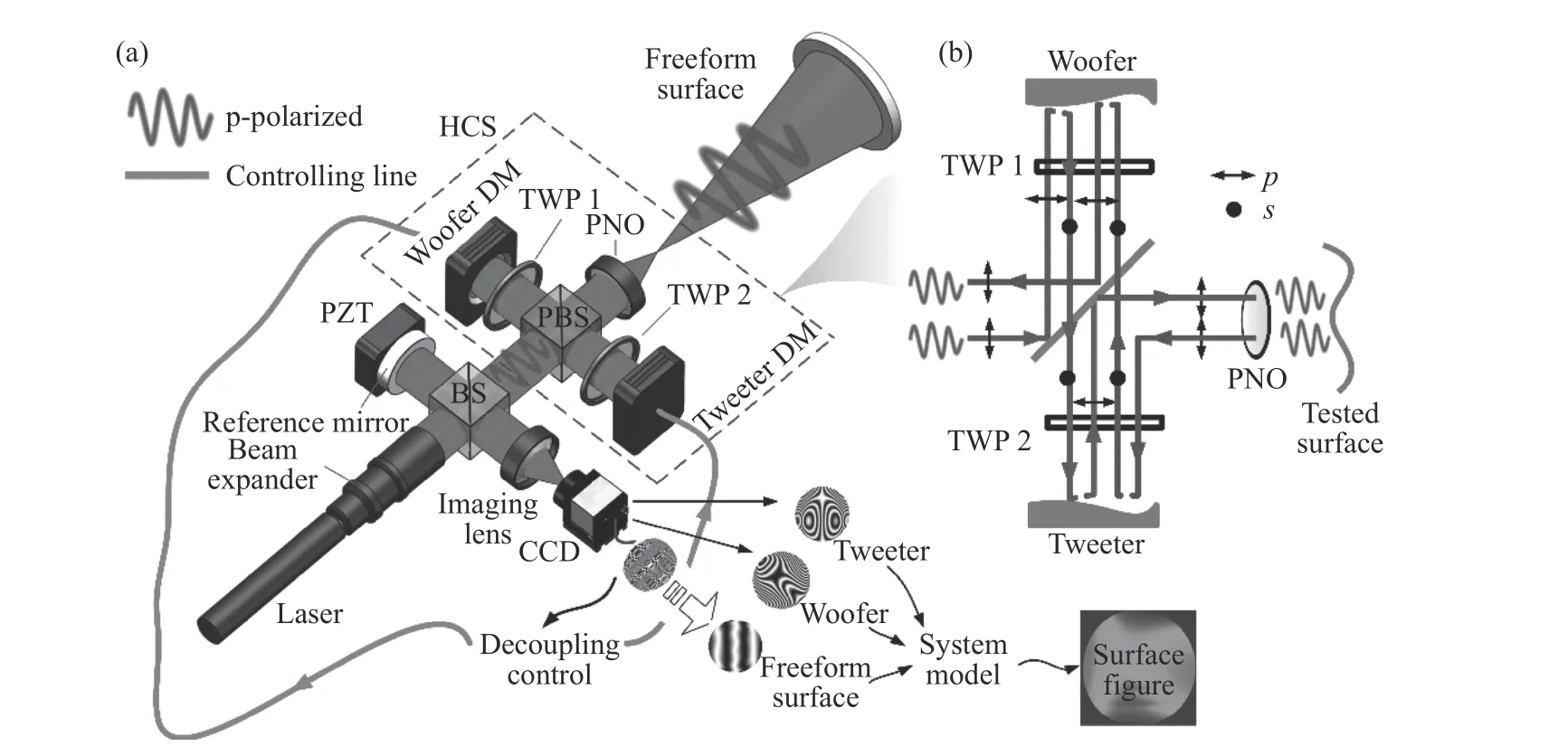
图14 双DM 级联的方式进行未知自由曲面自适应检测[61]。（a）系统布局；（b）系统偏振设计Fig.14 Adaptive interferometry of unknown freeform surfaces with cascaded DMs[61].(a)System layout;(b)polarization design

由于上述级联DM 虽然增加了检测动态范围，但是DM 监测和解耦算法操作复杂。基于该问题，2020 年，安徽大学自由曲面检测课题组报道了一种基于自适应环腔补偿器(Adaptive Ring-Cavity Compensator,ARCC)的干涉仪[64]，如图15（a）（彩图见期刊电子版）所示，采用单个DM 达到双DM 级联的动态范围。如图15（b）（彩图见期刊电子版）所示，其中ARCC 由单个DM、标准平面反射镜（Standard Mirror，SM）、λ/2 波片以及两个PBS 组成环形腔。进入ARCC 的光束将在其中经历2 个循环反射才能出射。ARCC 将DM 的像差校正量放大了两倍。通过在CCD 前安装一个可旋转的偏振片(RP)，可依次测量自由曲面和DM，不需要任何其他辅助装置。

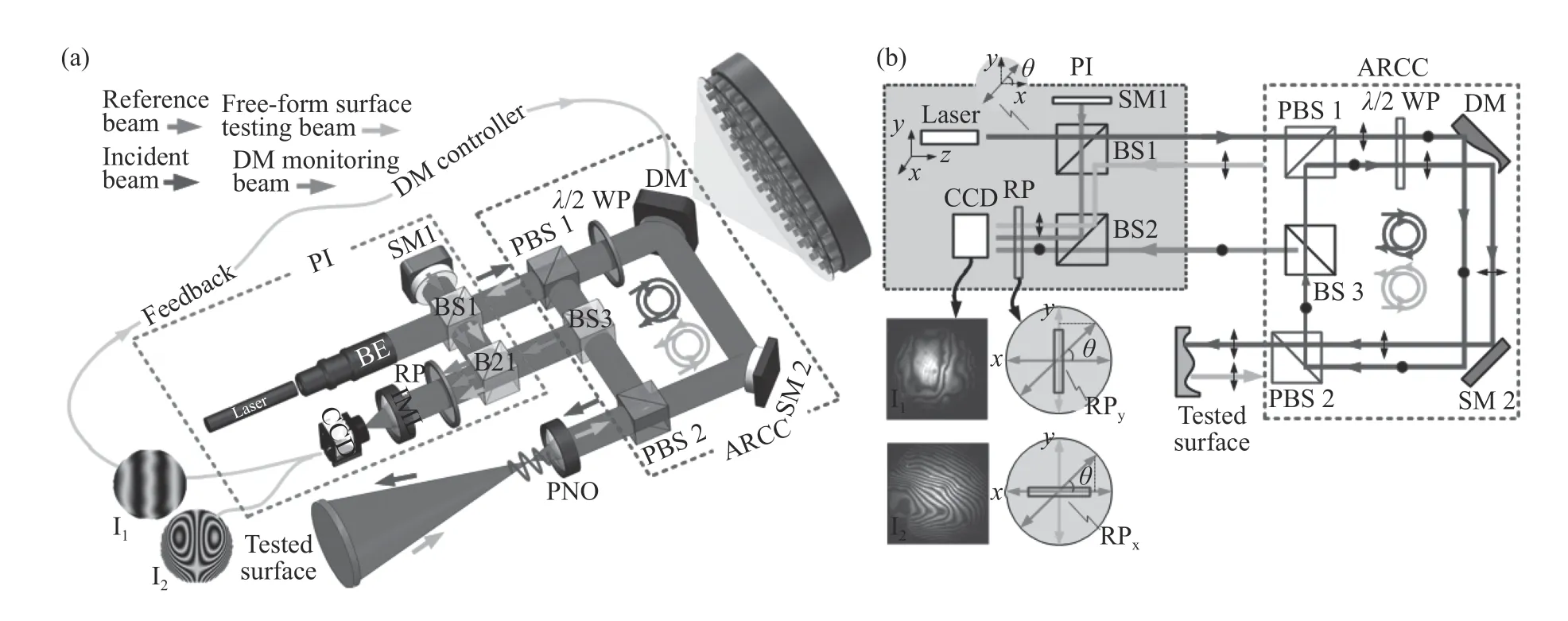
图15 基于自适应环腔补偿器的自由曲面干涉仪[64]。（a）系统布局；（b）偏振设计Fig.15 Freeform surface interferometer based on Adaptive Ring-Cavity Compensator(ARCC)[64].(a)System layout;(b)polarization design

4 自适应干涉检测控制算法

光学自适应控制算法经过了多年发展日趋成熟，传统的基于波前传感器的光学自适应控制是基于光瞳共轭面[65]或焦面前后光斑的波前相位优化[66]。1997 年Vorontsov[67]提出的SPGD 算法可实现像面信息直接闭环校正，开启了无波前传感器（WaveFront Sensor-less，WFS-less）的自适应控制。近年来发展起来的WFS-less 技术大多是通过焦面环围能量、峰值光强等指标来实现反馈控制[68−70]。而在自由曲面干涉检测中面临的优化指标是干涉条纹强度分布密度，因此，自适应干涉检测中的优化过程属于典型的WFS-less 自适应控制。通常，干涉条纹可以解调出波前Zernike相位，进而采用波前Zernike 系数指标优化。而自由曲面检测中首先面临的是无法分辨的甚至是部分缺失的干涉条纹，如图16 所示，这种情况难以实现相位解调，得到波前数据。

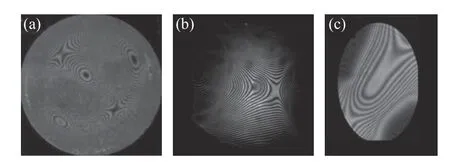
图16 自由曲面检测干涉图常见的3 种局部区域难以分辨甚至条纹缺失情形。（a）、（b）、（c）分别为文献[71]、[61]、[50]所述情形Fig.16 Freeform surface interferograms are generally difficult to identify in local areas and are even missing their fringe.(a)in Ref.[71],(b)in Ref.[61],(c)in Ref.[50].

2016 年，黄磊率先研究了自适应干涉检测中的优化控制技术[50]，采用SPGD 算法[53,54]进行DM 形变优化，以稀疏干涉条纹为最终优化目标。总体思想是以微扰方式不断更改驱动器电压，直到系统性能指标J达到预设的阈值。由于自由曲面干涉图一般可能存在局部难以分辨甚至条纹缺失的状态，难以使用固定的性能评价指标进行评价。SPGD 优化主要分为三个阶段：第一阶段为干涉条纹缺失区域恢复，以条纹缺失区域中任意两个象素之间灰度差的平方和（sum of squared gray level differences between any two pixels of the interferogram，SSD）为优化目标J，实现全口径干涉条纹显示，因此该优化方式可称为SSD-SPGD 算法。其具体实施方式如公式（1）～式（3）所示。

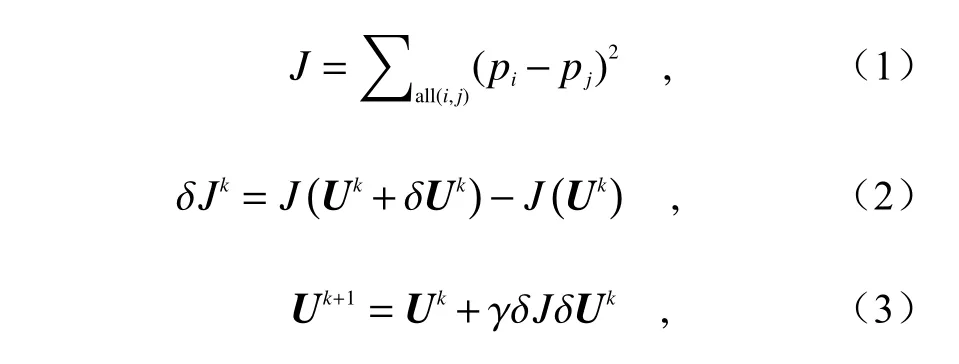
其中，U为执行器电压的控制信号矢量；k为迭代次数；γ 为增益系数；δJ是系统性能指标J的变量；δU是一种随机微扰，具有相同的振幅和伯努利概率分布；i和j为像素坐标；pi和pj为两个像素点灰度值。

由于上一步优化得到的干涉条纹密度较大，第二阶段以条纹PV 值替代优化目标J，获得稀疏干涉条纹；第三阶段直接以剩余波前像差Zernike系数为优化目标J，以获得近似零位条纹。如图17所示，随着条纹图案越来越清晰，J值也随之增加。SPGD 方法的收敛速度取决于许多因素，如DM 驱动器的数量、图像分辨率和计算机类型，一般典型的优化时间为6～9 min。

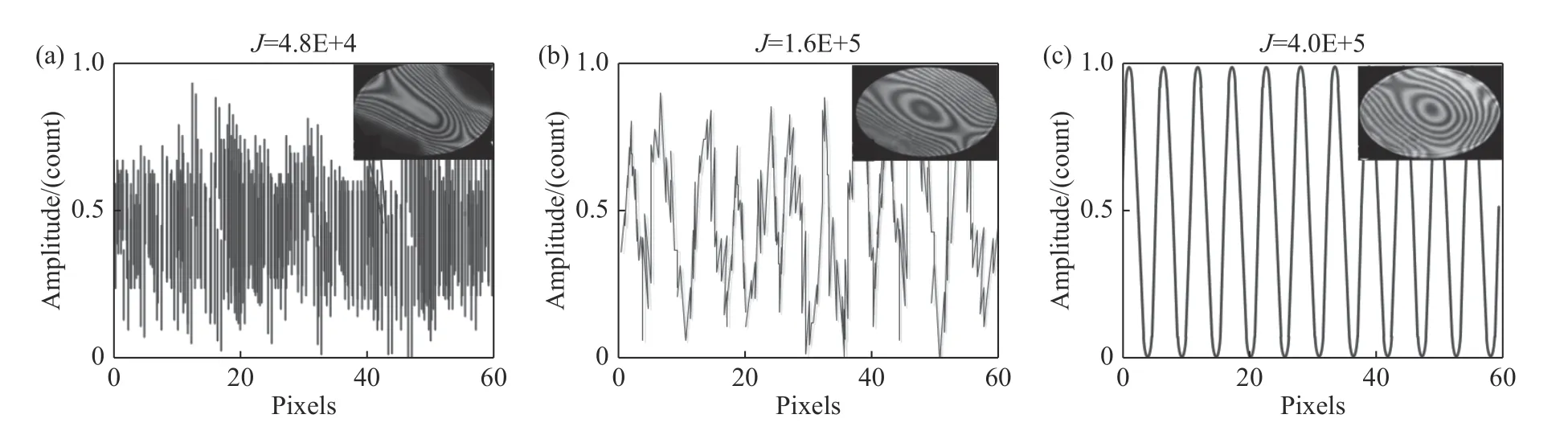
图17 SPGD 搜索过程中，以优化指标J 作为条纹恢复判据的一维演示。（a）为条纹缺失状态，（b）为优化中间过程，（c）为最终条纹及其J 值[50]Fig.17 One-dimensional demonstration showing the judgment valueJas the fringe restoration criterion during the SPGD search process.(a)The case without the fringe,(b)the middle of the restoration process,and(c)the final fringe with itsJvalue[50].

随后，Zhang Yu 等人[72]对上述SPGD 算法进行了改进，综合了SPGD 和Newton 迭代算法的优势，主要的自适应优化控制过程依然分为三步，第一步是利用SPGD 算法恢复干涉图中条纹缺失区域和，其评价指标J为条纹缺失区域像素灰度值I(i,j)之和

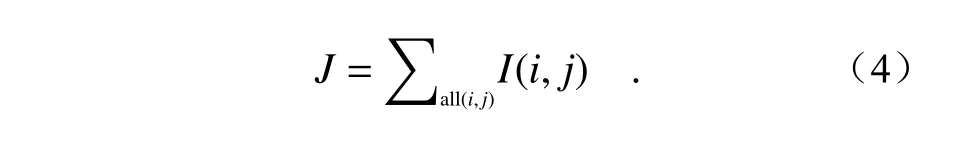
第二步利用SPGD 算法降低全口径条纹密度，评价指标J的定义如下

其中，Num 表示有效点的数量，在干涉图优化之前，需要对干涉图的有效域识别，I(i,j)是一个像素的灰度值，I′(i,j)是灰度值减去灰度均值Imean，Num1和Num2为I′(i,j)中正负相反的像素个数，J表示不同符号的像素数与有效像素总数的比例。

第三步利用牛顿迭代算法得到近似零条纹。该方法可有效缓解SPGD 算法迭代次数过多，无法得到最优值（近似全口径无条纹）的隐患。Newton 迭代算法主要思想如式（9）所示，其中，Zn是在每次迭代中驱动器的电压，Zn+1在每次迭代之后驱动器的新电压，ΔZn是电压的变化，f(Zn)是每一次迭代的相位分布，f′(Zn)是f(Zn)的偏导。

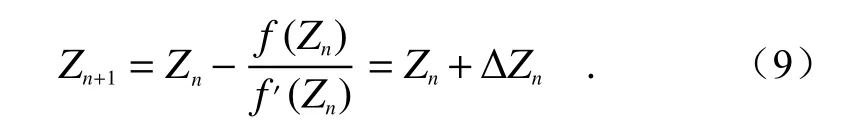
图18 展示了整体优化过程，图18(a)给出了第二步全口径条纹稀疏度评价指标J的变化情况；图18(b)和18(c)分别为利用Newton 算法和SPGD 算法时，全口径条纹RMS 值的收敛状态，可见，牛顿迭代的收敛速度较快，经过2 次或3 次迭代后即可收敛至极小值。

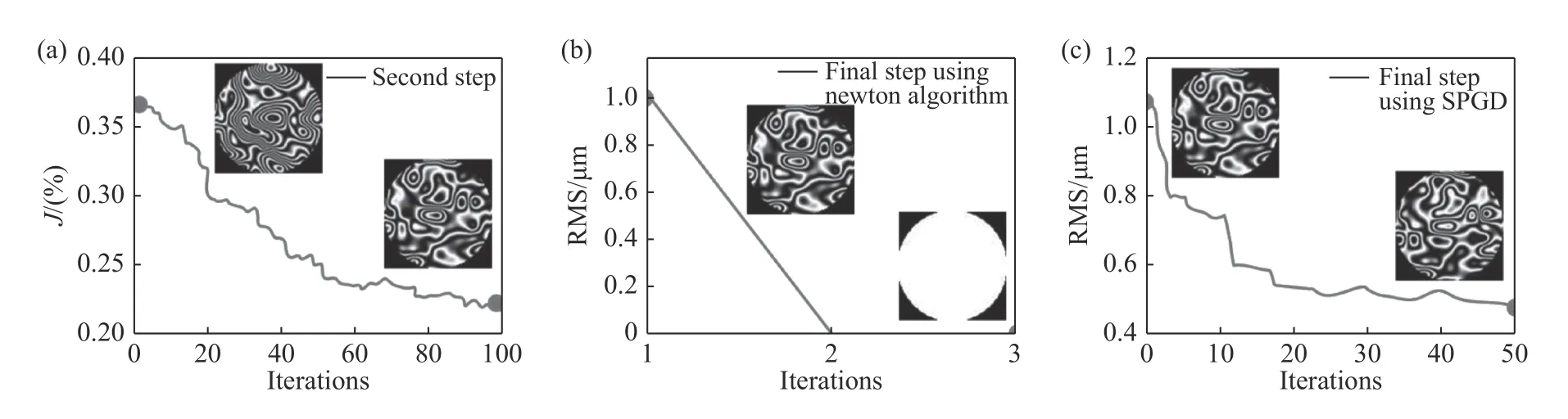
图18 实验中优化收敛曲线。（a）SPGD 算法的收敛曲线(第二步)；（b）最后一步采用牛顿迭代算法时的收敛曲线；（c）最后一步采用SPGD 算法时的收敛曲线[72]Fig.18 Experimental convergence curves between the second and final steps.(a)The convergence curve using the SPGD algorithm(the second step);(b)the convergence curve using the Newton iteration algorithm in the final step;(c)the convergence curve using the SPGD algorithm in the final step[72]

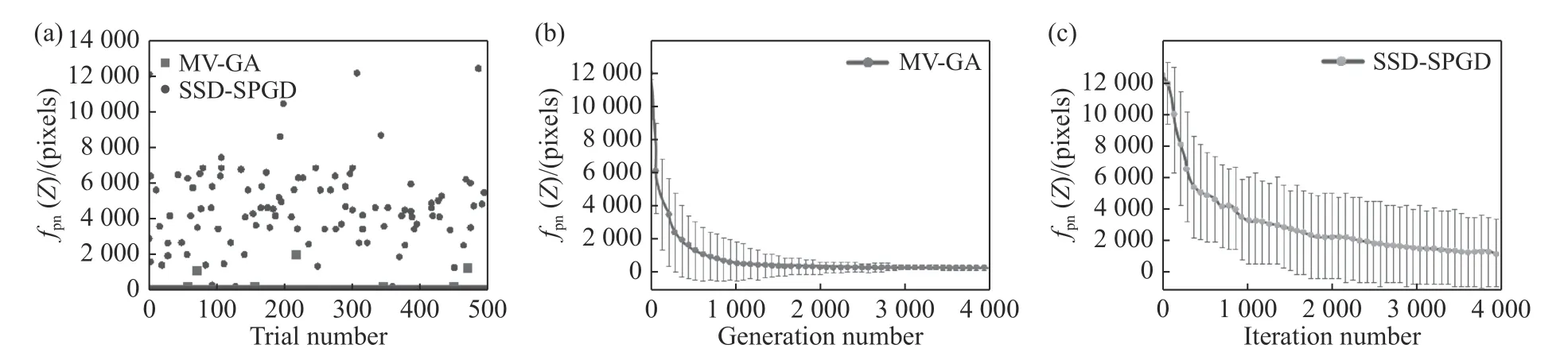
图19 MV-GA 和SSD-SPGD 算法对比[71]。（a）500 次实验中MV-GA 和SSD-SPGD 算法优化后的目标函数值（最终干涉图中不可分辨条纹子区域的像素数），（b）MV-GA 法中500 个试验目标函数值的均值变化，（c）SSD-SPGD 算法500 次试验目标函数值的均值随迭代次数的变化Fig.19 Comparison of the MV-GA and SSD-SPGD algorithms[71].(a)The objective function values optimized by MV-GA and SSD-SPGD in 500 experiments.(b)Variation of the mean value&standard deviation of the 500 trials’objective function values with a generation number for the MV-GA method.(c)Variation of the mean value&standard deviation of the 500 trials’objective function values with the iteration number for the SSD-SPGD method.

5 现状分析与发展趋势

虽然一些新的自适应元件，如液晶透镜[73−76]，也已经被用于大动态范围的光学调控和测量中，目前自由曲面的干涉检测研究主要还是集中在基于LC-SLM 和MEMS-DM 的补偿器上。基于SLM 的自由曲面自适应干涉检测的优点是检测结构简单，空间分辨率高，相位调制的控制精度较高，可直接与商业干涉仪兼容，但其相位控制算法相对复杂。国防科技大学的陈善勇和薛帅课题组[38−40,71]和罗切斯特大学[41]都在该领域进行了研究。从基于DM 的自由曲面自适应干涉检测近年的发展来看，其与光路偏振设计相结合可以很好地满足自由曲面加工阶段未知面形原位检测的需求，由于DM 面形控制的固有特性，其用于高精度干涉检测中唯一需要解决的问题是其本身面形精度的监测。亚利桑那大学R.Liang 课题组[50,72]和安徽大学张磊课题组[55,56,61,64]均在该领域取得了一定进展。

5.1 精度

传统零位或非零位干涉检测的精度已有很多文献进行了分析。自适应干涉检测中，精度在很大程度上受限于自适应光学元件的相位调控精度，SLM 的相位调制精度主要依赖其相位控制算法精度，同时也和其自身产生的波前调制量有关，目前最新实验报道精度可达λ/30 rms（λ=632.8 nm，～20 nm）；目前DM 的精度主要依赖于其原位监测和建模精度，精度与波前调制量呈反比，目前补偿40μm 非旋转对称偏离度的自由曲面实验精度可达8 nm(rms)。最终实验精度实际上和传统干涉仪一样。对比表1和表2，对于同级别偏离度自由曲面检测，基于DM 的自适应干涉检测精度略高于基于SLM 的检测精度。

5.2 动态范围

目前，实验报道的基于SLM 的自适应干涉检测最大动态范围约20μm，基于单个DM 的自适应干涉检测最大动态范围约40μm。通过级联自适应元件可增加动态范围，但是SLM 的级联并非易事，因为其基于衍射的工作机理给后续级联的SLM 相位控制带来困难；而基于反射机制的DM级联则相对容易。随着大波前调制量的自适应光学元件的应用系统结构设计，自由曲面干涉检测的动态范围将不断扩大，甚至无需传统的零位镜辅助，即可实现全口径大偏离度检测。R.Chaudhuri基于150μm 偏离度自由曲面的SLM 的干涉检测模拟则是最好的证明。然而，采用DM 的自适应干涉检测时，结论却并不是如此。双级联DMs不仅可以使得相位调制量增加，还可以通过驱动器排布增加分辨率，而相同孔径的单个DM 中即使驱动器数量达到二者之和，也难以达到二者级联所达到的相位调制量，这是因为采用高密度驱动器的DM 通常是为了进行高阶像差矫正而设计的，一般行程较小，而低密度驱动器行程相对较大，但分辨率相对较低，仅适合矫正低阶像差。即使有一个同样相位调制量的DM，成本也会很高，而且一般干涉仪也无法监测具有如此大冲程的DM。级联DM 干涉仪则很好地解决了这一问题，因为级联DM 可分担像差补偿，而干涉仪只需对DM 进行逐个监测。这意味着级联DMs 技术是利用干涉仪检测大偏离度自由曲面时的首选方法，一味追求大波前调制量的单个DM 反而会给干涉检测带来困难，除非放弃干涉检测，转而寻求其他方式进行DM 监测[50]。

5.3 系统集成度

基于SLM 的干涉仪集成度相对较高，也可与商业干涉仪直接配合使用；基于DM 的干涉仪最大的缺点是需要辅助监控设备或结构来保证DM 像差的补偿精度。通过光路的偏振设计和光路中偏振器件的旋转，可利用同一CCD 实现DM 的监控和自由曲面的检测（时分复用），因此就损失了一定的实时性，若DM 的开环稳定性较高，则其实时监控要求可放松，特别是对于级联DMs，普通监控方法需要三个CCD 分别对针对两个级联DM 监控和被测面检测，这将使得系统更加复杂。而时分复用方法则极大地简化了系统，除了干涉仪本身外，不需要其他设备来进行DMs的监控。这样基于DM 的干涉检测也可配合商用干涉仪使用。

5.4 自适应控制算法

与传统自适应控制算法不一样的地方在于目前的自适应干涉控制算法的优化评价指标是干涉强度分布，而在优化搜索过程中，具体评价指标是跟随优化阶段而变化的。一般情况下，自适应控制算法主要都分为三步（或两步），第一步是恢复条纹缺失区域的条纹，第二步是将密集条纹转化为稀疏条纹，第三步将稀疏条纹零位化，有时第二、三步可合并为一步。目前报道的算法中，SPGD算法和GA 算法均能胜任自由曲面自适应干涉检测中的优化控制，其中SPGD 算法的时效性优于于GA 算法，而GA 算法的收敛性优于SPGD 算法。但正如文献所述，GA 算法也可以满足高精度干涉检测的时效性要求，加之，其高收敛性更适合用于不同自由曲面形态的检测。未来还可以将深度学习的自适应控制方法引入干涉检测中[77-78]。当然，开环自适应算法[79-82]若能进一步提高精度，也将能被自适应干涉检测广泛采用。

表1 和表2 分别列出了最新研究报道中使用的DM 和SLM 的参数及自由曲面检测指标。

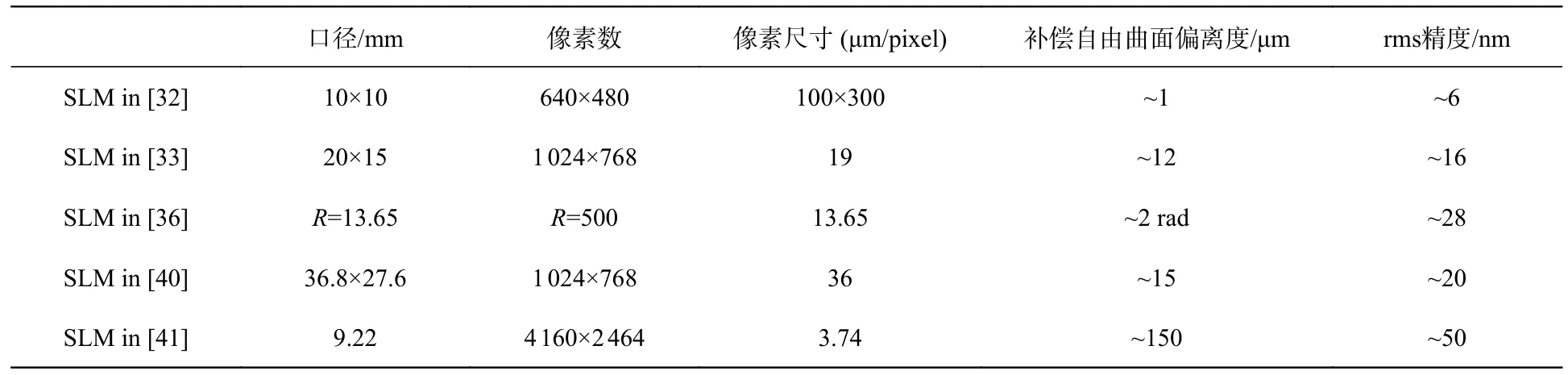
表1 相关文献研究中使用的SLM 参数及自由曲面检测指标Tab.1 SLM parameters used in relevant literatures and freeform surface detection indexes

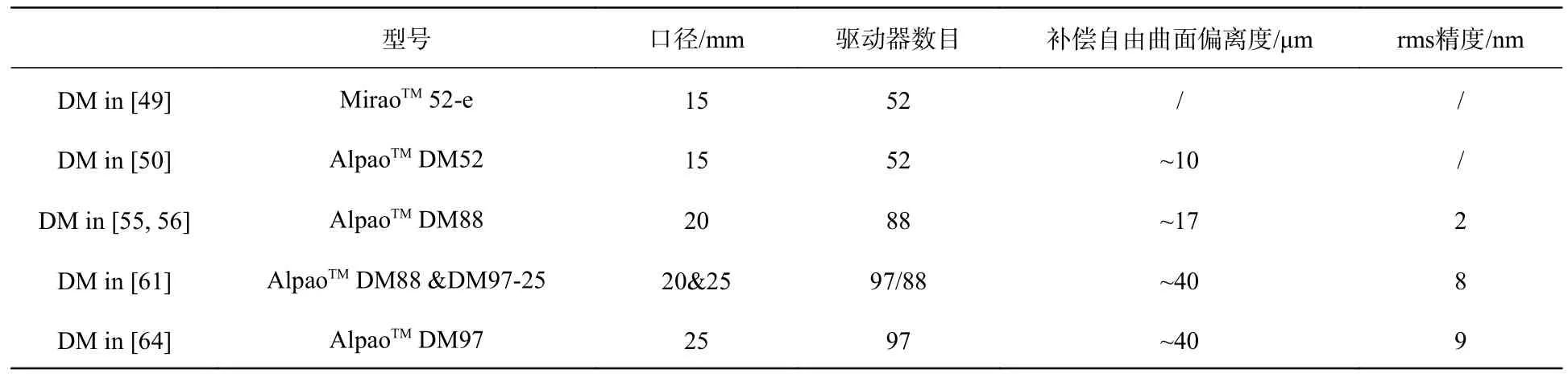
表2 相关文献研究中使用的DM 参数及自由曲面检测指标Tab.2 DM parameters used in relevant literatures and freeform surface detection indexes

6 结束语

本文介绍了光学自由曲面自适应干涉检测的原理、器件、发展历程及最新进展。由于自适应光学元件具有动态可编程的优势，可作为动态补偿器参与自由曲面高精度干涉检测。近年来，围绕自适应干涉检测的研究主要针对LC-SLM 和MEMS-DM 展开。基于LC-SLM 的自由曲面自适应干涉检测的优点是检测结构简单，空间分辨率高，相位调制的控制精度较高，可直接与商业干涉仪兼容，但其相位控制算法相对复杂，国内国防科技大学和美国罗切斯特大学对这一技术正在展开研究。未来基于LC-SLM 的自适应干涉检测的研究依然集中在大动态范围SLM 的使用以及高精度的波前调制算法。DM 的自适应干涉检测优势是相位调制方式简单，基于反射原理的相位调制可以通过器件级联实现叠加，光路调整与校准简单。国内安徽大学与美国亚利桑那大学正在开展相关研究。未来的研究将仍然为DM 与被测面的同时监测。另外，快速、全局、收敛率高的自适应控制算法也是研究重点。