深部岩体水力劈裂分析及临界水压力计算

左拥军

（万年县水利局，江西万年335500）

0 引言

水力劈裂是指岩体或者其他脆性材料在高水头作用下，其内部裂纹发生扩展及贯通现象[1]。岩体内部结构因水力劈裂作用而改变，导致渗透性增加，同时，渗透性的增加又会导致渗流速度增加，使得水力劈裂作用进一步增强，如此循环，最终使得整个岩体结构发生破坏。深埋水工隧洞施工时出现涌水、高压输水构筑物发生破裂渗漏等均是水力劈裂造成工程事故的典型例子[2]。

水力劈裂最初是应用于石油行业，随着水利水电工程的迅速发展，越来越多的工程建设中均涉及到水力劈裂问题。崔少英等[3]通过对水工隧洞中水力劈裂临界孔隙水压力进行了研究，并得出了3 种类型裂缝和无裂缝情况下的临界孔隙水压力计算方法。黄润秋等[4]对围岩发生水力劈裂时，隧道出现涌水现象进行了研究，认为当裂纹面受到法向压应力时，其裂纹的扩展多表现为Ⅱ裂纹问题，并给出了临界水压力的计算判据。本文针对深部岩体出现的水力劈裂现象进行分析，利用断裂力学理论，在拉剪、压剪复合型破坏模式下，深部岩体原裂纹方位角和侧压力系数对临界水压力的影响规律进行深入研究。

1 岩石断裂破坏模式

关于陶瓷、金属等材料的裂纹扩展问题，最早是采用经典断裂力学进行研究的。裂纹附近远场应力主要是拉力和剪力，而自然界中岩体内裂纹在构造应力和地应力作用下多处于受压状态，加上岩体自身结构构造的特殊性，大量文献表明，岩石类材料与金属材料之间的断裂力学行为有很大差别。若当岩体处于地下深部时，此时还会受到孔隙水压力的作用，其断裂破坏模式更为复杂。因此，远场地应力、垂直和水平地应力的相对值及孔隙水压力是影响深部岩体内裂纹失稳扩展的主要因素。由此可知，要进行深部岩体临界水压力的计算，必须先判别其破坏模式。

1.1 力学模型的建立

岩体内裂纹的分布是不均匀的，为方便计算，本文建立了含闭合单裂纹岩体的计算模型，如图1所示，其目的是研究孔隙水压力对深部岩体断裂模式的影响及临界水压计算。图中σ1和σ3为闭合裂纹受到的远场地应力，α为闭合裂纹与垂直方向上的地应力σ1之间的夹角（裂纹方位角），闭合裂纹内作用有孔隙水压力p。假设孔隙水压力沿裂纹各个方向的作用力是相同的，岩体为脆弹性，则根据应力状态分析可知，此时裂纹面上的正应力σα和剪应力τα分别为：

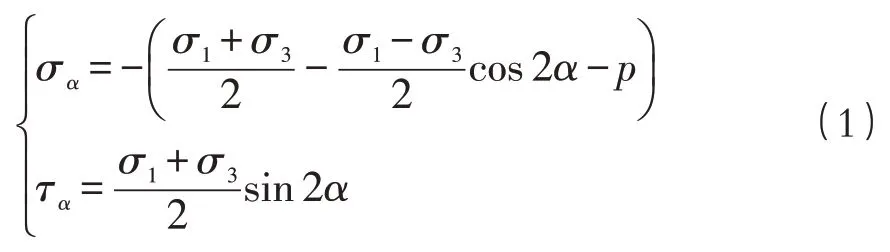
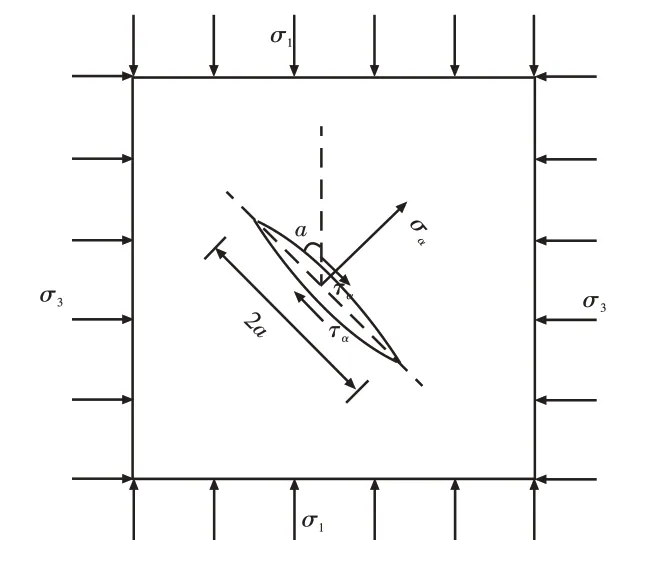
图1 含单裂纹岩体计算模型

1.2 裂纹失稳扩展模式

由于裂缝面上的应力在断裂力学中规定受拉为正、受压为负，而岩石力学中的规定与之相反，所以需在式（1）前面加上负号。由式（1）可知，裂缝面上既存在正应力又存在剪应力，因此，裂纹失稳扩展问题应属于Ⅰ-Ⅱ复合型裂纹问题。此时裂缝面上的正应力σα有两种情况。

1）当裂缝面上的正应力σα为拉应力时，裂纹的失稳扩展问题应属于拉剪复合型问题。目前，对于拉剪复合型裂纹断裂准则，有最大周向应力理论、应变能密度因子理论及能量释放率理论，这些准则由于在计算中比较繁琐，使得工作量较大，且不易得到临界水压力的计算显示。基于此，本文采用近似断裂准则，得到拉剪复合型裂纹失稳准则：

式中：KⅠc为Ⅰ型断裂韧度；KⅠ为Ⅰ型应力强度因子；KⅡ为Ⅱ型应力强度因子。

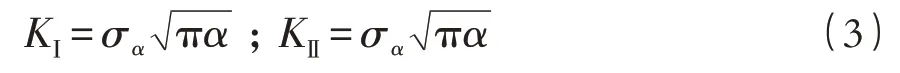
式中：α为闭合裂缝半长。

2）当裂缝面上的正应力σα为压应力时，裂纹的失稳扩展问题应属于压剪复合型问题。关于岩体的压剪断裂机制，大量研究表明[3，4]，岩体内的裂纹在压剪复合应力状态下，裂纹会逐渐闭合直至压紧，随后裂缝面间会发生相对滑动，受岩体的节理构造及组成晶格等因素影响，裂缝面在发生滑动时其裂纹尖端会出现明显的剪胀现象，而围压又会抑制这种现象。因此，岩体在压剪复合应力状态下的断裂机理十分复杂，导致关于压剪断裂破坏机理还未形成一套完整的、被工程所认可的准则。基于此，本文就文献［5］提出的经验准则对岩体的压剪特性进行研究，计算公式如下：

式中：λ为压剪参数，可由试验获取；为处于压缩状态下岩体的Ⅱ断裂韧度。式（4）中，当KⅡ为0 时，则为Ⅰ型断裂，即：

由式（5）可知，λ反应了处于压缩状态下的岩体材料Ⅱ断裂韧度与其Ⅰ断裂韧度的比值。

2 岩体裂纹失稳临界水压力计算

2.1 拉剪状态下的临界水压力

假设岩体内裂纹失稳扩展时的孔隙水压力为临界水压力，将式（1）代入式（3），再代入式（2）即可得到岩体在拉剪状态时的临界水压力，计算公式如下：

式（7）中m为侧压力系数，反映了裂纹周围围压的大小，而围压关系着岩体内裂纹失稳扩展方向。因此，分析侧压力系数对临界水压力的影响是有必要的。

根据式（7），可得到在不同侧压力系数下的广义临界水压力与裂纹方位角的关系，如图2 所示。由图2 可知，随着侧压力系数的增加，广义临界水压力也在逐渐增加。当m＜1.0和α=0°时，广义临界水压力取得最小值，由此可知，当原裂纹处于垂直方向时，易发生水力劈裂现象；当m=1 时，广义临界水压力为一定值，与原裂纹方位角无关，此时裂纹各个方向的受力状况相同；当m＞1.0和α=0°时，广义临界水压力取得最小值，即当原裂纹在水平方向时，易发生水力劈裂现象。

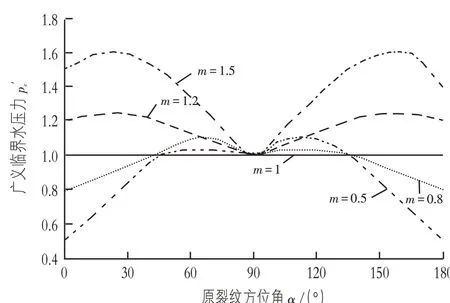
图2 拉剪状态下广义临界水压力与原裂纹方位角的关系

2.2 压剪状态下的临界水压力

据上文分析可知，压剪状态下，裂缝面最终会发生相对滑动现象，此时裂缝面间的有效剪应力τe是导致裂纹失稳的主要因素，其计算公式为：

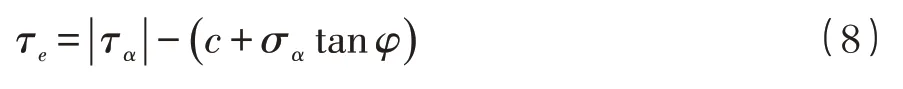
式中：φ为裂缝面间的内摩擦角；c为裂缝面间的粘聚力。

根据公式（4）得到压剪状态下裂纹失稳扩展时的广义临界水压力：

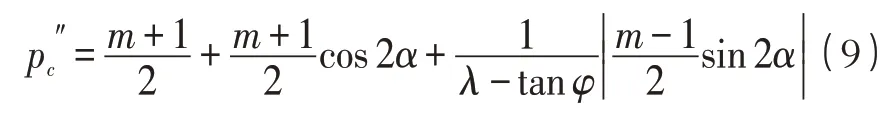
式中：所表示的含义同拉剪状态下的一样，但其具体表达式不同，即：

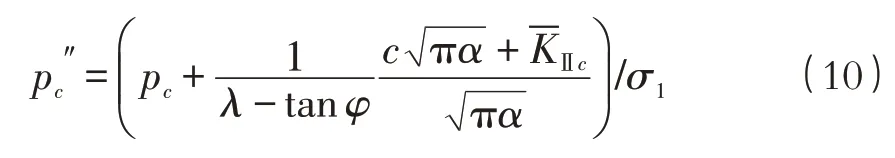
其中需注意：1）公式（4）需在压应力为正的条件下方可得到，所以式（8）～（10）中，σα也需在压应力时取正；2）由于莫尔-库仑准则表示的是极限状态时的关系，式（8）中的有效剪应力需大于0 才能使式（9）成立；3）在计算中得到的临界水压力还需满足式（1）小于0，否则表示在该条件下裂纹失稳扩展时不会发生压剪复合断裂。

不同侧压力系数下的广义临界水压力与裂纹方位角的关系，如图3 所示。由于式（9）中（λ-tanφ）的正负号未确定，得到的广义临界水压力会有差异。因此，在计算过程中引入文献［7］的数据：1）当（λ-tanφ）＜0 时，取λ=0.3，tanφ=0.365；2）当（λ-tanφ）＞0 时，取λ=0.7，tanφ=0.365。由图3（a）可知，当（λ-tanφ）＜0 时，所有曲线（m= 1 时除外）均在45°和135°时取得极小值。侧压力系数越接近1，广义临界水压力越大，并在m= 1 时取最大值；当（λ-tanφ）＞0 时，其广义临界水压力的分布规律基本同拉剪复合断裂模式下的一致。

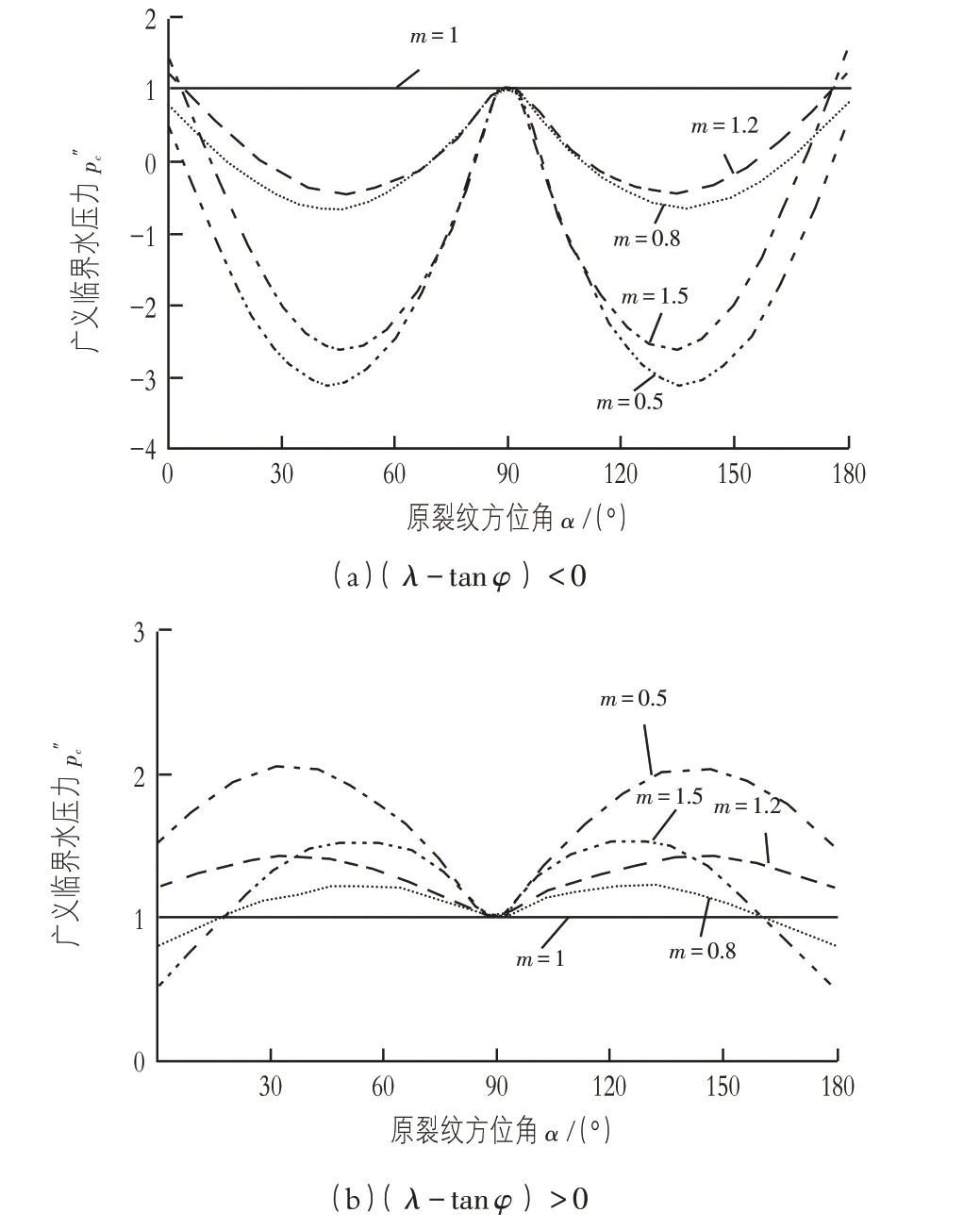
图3 压剪状态下广义临界水压力与原裂纹方位角的关系

3 结语

由于深部岩体内裂纹会受到孔隙水压力的作用，其失稳扩展时会发生拉剪复合断裂或压剪复合断裂。因此，对于不同情况下的破坏模式，需进行分别讨论。上文针对深部岩体，对其内部裂纹失稳扩展的破坏模式进行的研究，得出以下结论：

1）深部岩体内裂纹的扩展无论是压剪复合型还是拉剪复合型，只要当侧压力系数为1 时，其临界水压力均不会因原裂纹方位角的改变而改变。

2）当裂纹的扩展属于拉剪复合断裂问题时，临界水压力会随着侧压力系数的增加而增加。当侧压力系数m＜1.0 和原裂纹方位角α=0°时，原裂纹在垂直方向最容易发生水力劈裂现象；当侧压力系数m＞1.0 和原裂纹方位角α=90°时，原裂纹在水平方向最容易发生水力劈裂现象。

3）当裂纹扩展属于压剪复合断裂问题时，临界水压力的分布规律受（λ-tanφ）的正负号的影响。当（λ-tanφ）＞0时，其临界水压力的分布规律与拉剪复合断裂时的基本一致；当（λ-tanφ）＜0时，原裂纹在方位角为45°和135°时，最容易发生水力劈裂现象。