温度引起的流体非牛顿特性研究*

孙光湧 黄 平

(华南理工大学机械与汽车工程学院 广东广州 510640)

通常按照本构方程是否符合牛顿黏性定律，将流体分为牛顿流体和非牛顿流体。与牛顿流体不同，非牛顿流体的剪应力与剪应变率之间不是线性关系。事实上，任何流体都具有不同程度的非牛顿性。通常牛顿流体在一般工况下不会表现出非牛顿性，但在高压、高剪切率的工况下也会表现出一定的非牛顿性。

在润滑理论的研究当中，常用到的非牛顿流体本构方程[1]有

(1)Ree-Eyring本构方程

(1)

式中：τ0为特征应力；η0为液体在低剪切应力时的动力黏度。

(2)黏塑性本构方程

图1中曲线2为极限剪切流体的流变特性。令τL为极限剪切应力，其变化规律可描述如下

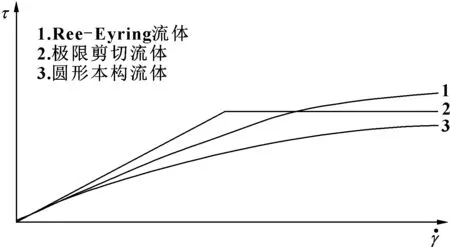
图1 各类流体模型本构曲线

(2)

(3)圆形本构方程

(3)

一直以来有许多关于非牛顿流体本构方程的研究。郑连存和韩世豪[2]提出Maxwell黏弹性流体流变协同的传热本构方程模型。贺丽萍[3]推导出了相应的适合幂律型非牛顿流体圆射流的本构方程和控制方程。吴铿等人[4]建立了熔渣的本构方程,确定了流变特性参数,并探明温度和添加物对熔渣流变特性的影响规律。袁祖强和刘建华[5]证明了幂指式流变模型完全符合添加剂与机械油混合流体的本构方程。陈晋南等[6]发现在相同条件和不同剪切率下分别测量得到的拟本构方程参数，更能合理描述物料的流变性能。柴增田等[7]利用幂律黏度模型，构建了模料流体的本构方程。还有许多学者在本构方程的研究中也取得了一些进展[8-11]。

工业生产的过程是极其复杂的，很难得到加工过程中的精确数学模型，所以经验在工业实践中占了很大的比重。而理论研究可以在改进产品的过程中起到方向性、指导性的作用。对于本构方程的研究，可以在理论角度描述加工的过程，可以很好地描述流体的流变性质[12]。因此对本构方程的研究至关重要。

随着人们对极限工况下润滑状态研究的深入，发现实际情况下出现了理论计算中没有预料到的润滑失效现象[13]。事实上在实际工况中，剪切速率的提高会导致温度的变化，而温度变化又会导致润滑液的黏度发生变化，黏度的变化又会影响润滑过程的分析，所以这几个因素是相互关联，相互影响的。本文作者通过求解合理简化后的能量方程，得到润滑过程中温度关于剪应变率的表达式，将其与Reynolds黏度方程一起代入牛顿黏性定律后，即得到了考虑温度效应的非牛顿流体本构方程，并分析温度引起的流体非牛顿特性变化。

1 温度本构方程的推导

1.1 已知条件

(1)一维能量方程的表述[14]如下

(4)

式中：p为压力；cp为在压力p下的比热容;ρ为润滑液密度;u为x方向速度;w为z方向速度；T为温度；k为导热系数;η为润滑液动力黏度。

各参数的定义可参照图2所示的楔形界面润滑示意图。

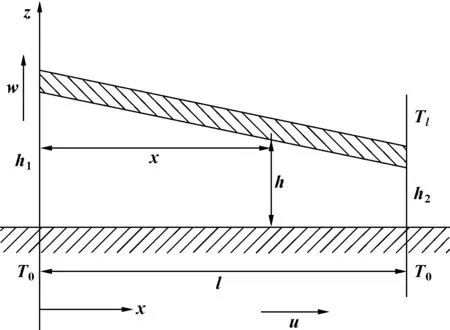
图2 楔形界面润滑示意

(2)Reynolds黏度方程

η=η0e-β(T-T0)

(5)

式中:η0为温度为T0时的动力黏度;β为黏温系数；通常可近似取β=0.03 K-1。

(6)

(4)牛顿黏性定律

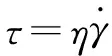
(7)

式中：τ为剪切应力。

1.2 假设条件

为了使研究问题简化，文中考虑平行板间的润滑情况，可参考图3所示的平板界面润滑示意图[1]。

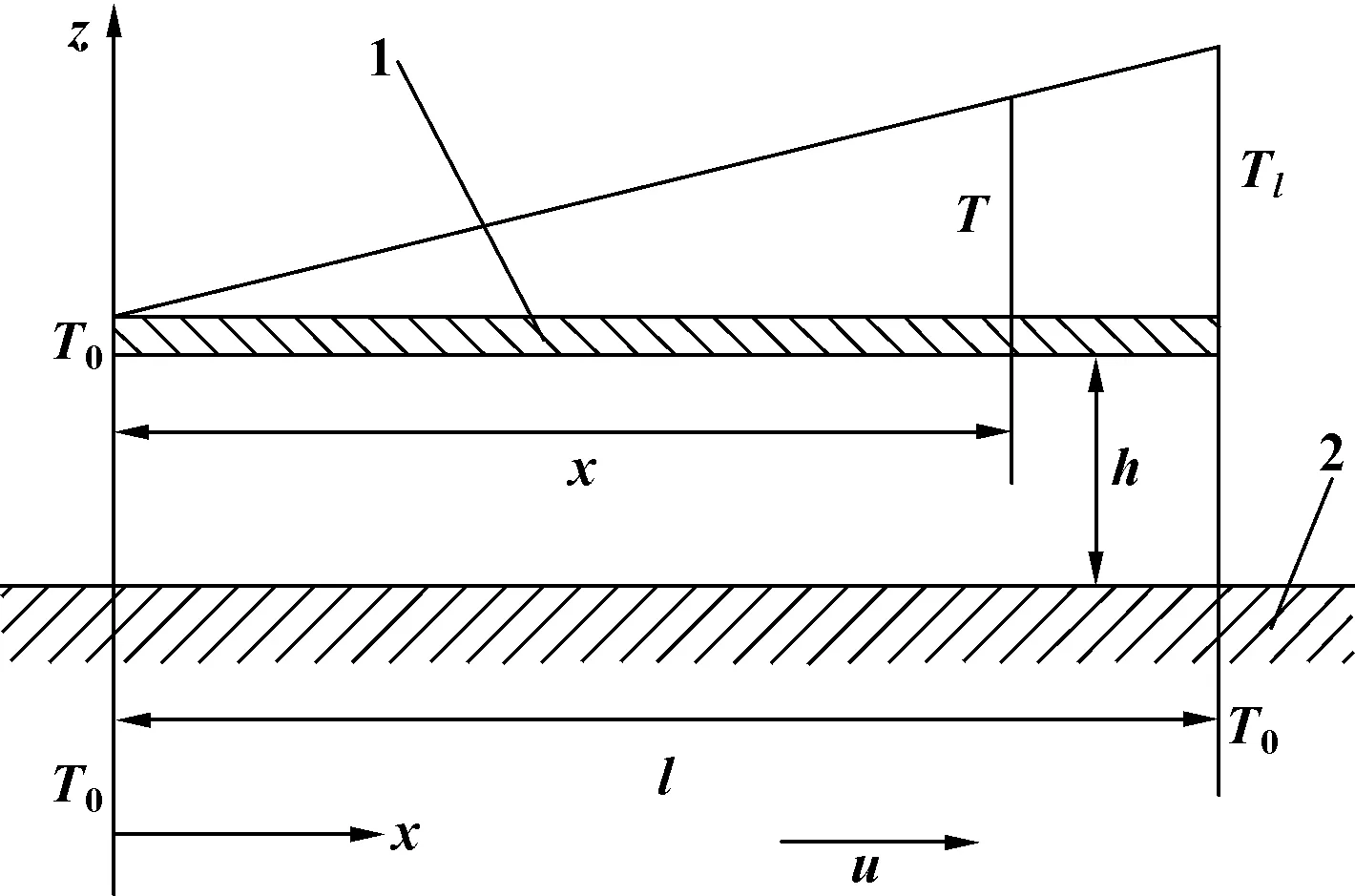
图3 平板界面润滑示意

在平板润滑情况下，可以得到

(1)z方向速度w=0；

(3)平板情况下压力p不存在，即便为楔形板情况，压力p对润滑过程的影响也非常小[14]。

另外，考虑到润滑油膜非常薄，也就是说h很小，所以可以假设温度T与z方向无关，即∂2T/∂z2=0。

1.3 公式推导

公式推导思路可以参考图4所示的公式推导流程。

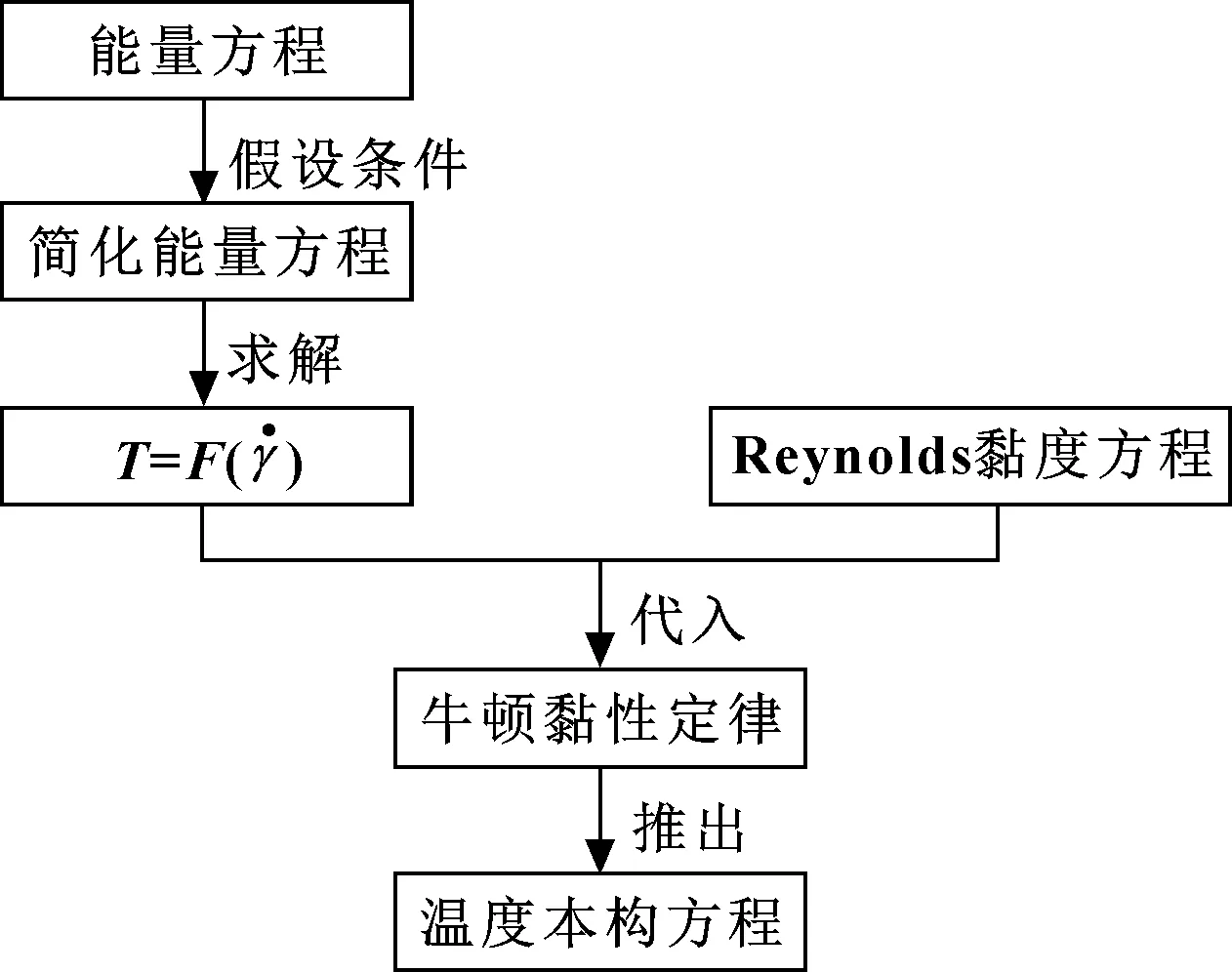
图4 公式推导流程

考虑1.2节的假设条件后，式(4)所示的一维能量方程可简化为

(8)

(9)

分离变量得到

(10)

两边取积分

(11)

式中：C为常数。

当x=0时，T=T0，求得

(12)

所以得到温度T关于位置x的关系式为

(13)

假设平板长度为l，则当x=l时，T=Tl

(14)

求取整个接触过程中的平均温度Tm

(15)

将平均温度Tm代入牛顿黏性定律方程中，得到

(16)

(17)

(18)

右边上下同除eβT0/2后，整理得到

(19)

式(19)为考虑温度效应的非牛顿流体本构方程。

2 黏温系数的实验确定

2.1 材料及仪器

主要材料：超纯水，江苏沭阳希之梦商贸有限公司生产；聚氧乙烯(PEO)，上海伊卡生物技术生产，相对分子质量60万。

主要仪器：DF-101S集热式磁力搅拌器；HAKKE Rheo Win Mars40流变仪。

2.2 黏温特性测量

实验前使用超纯水配置质量分数1%的PEO水溶液[15]，经DF-101S集热式磁力搅拌器充分搅拌溶解，得到均质液体，静止24 h未出现沉淀。

使用HAKKE Rheo Win Mars40流变仪对PEO水溶液黏温特性进行测量，采用Reynolds黏度方程对得到的数据进行拟合，得到图5所示的黏温曲线。

图5 1%PEO溶液黏温曲线

其中拟合得到初始黏度η0=0.095 Pa·s，黏温系数β=0.017 K-1，初始温度T0=3.48 ℃，校正决定系数R=0.997。

2.3 主要工况参数的取值

经过实验测量以及一定的假设，最终选取表1所示的数据为实际工况参数。

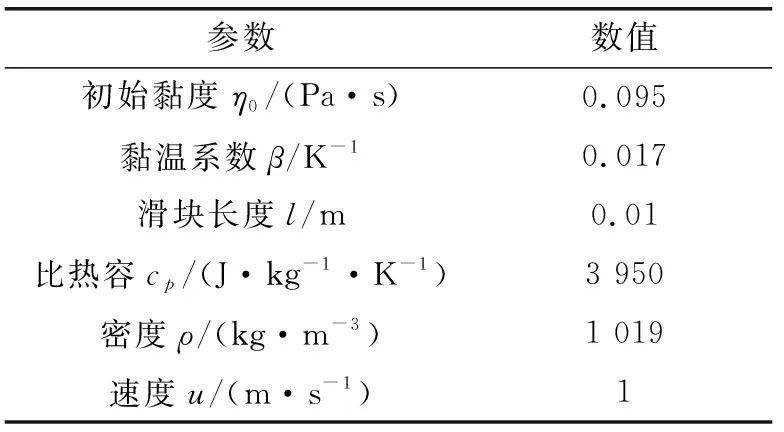
表1 实际工况参数取值

3 不同位置温度本构的变化分析

3.1 基于平均温度的本构方程

将表1中的数据代入温度本构方程(19)可以得到

(20)

由式(20)绘制的平均温度本构曲线如图6所示。

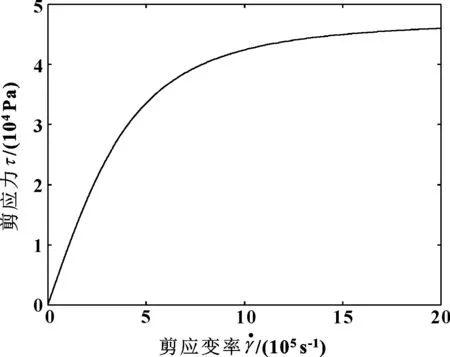
图6 平均温度本构曲线

图6中的最大值在右侧末端取得，剪应力为46 017 Pa。

从图6中可以看出，在曲线的前段，剪应变率从0到2.5×105s-1变化过程中，剪应力随之几乎线性增加，曲线斜率几乎不变，即润滑液黏度不变，表现出牛顿流体的性质；在曲线的中段，剪应变率从2.5×105s-1到1.5×106s-1变化过程中，曲线的斜率开始慢慢变小，润滑液出现剪切稀化现象；曲线的末端，在剪应变率大于1.5×106s-1时，剪应力随着剪应变率的增大非常缓慢地增加，曲线慢慢趋近于水平直线，润滑液黏度越来越小，慢慢趋近于0。整个过程中剪应力持续上升，可以保持有效润滑。

3.2 基于出口处温度的本构方程

式(19)是将整个接触面的平均温度代入牛顿黏性定律后得到的本构方程，实际情况下，润滑失效常发生在接触面的末端，也就是润滑过程的出口处。由式(13)可以看出温度T是随着x增大而增大的，所以出口处是整个接触过程温度变化最大的位置，那么这一位置的润滑情况就更值得分析。

将出口处的温度Tm代入牛顿黏性定律方程中，则得到

(21)

式(21)即为出口处温度本构曲线。

同样取与表1相同的实际参数，可以得到

(22)

由式(20)、式(22)绘制的平均温度本构曲线和出口处温度本构曲线如图7所示。

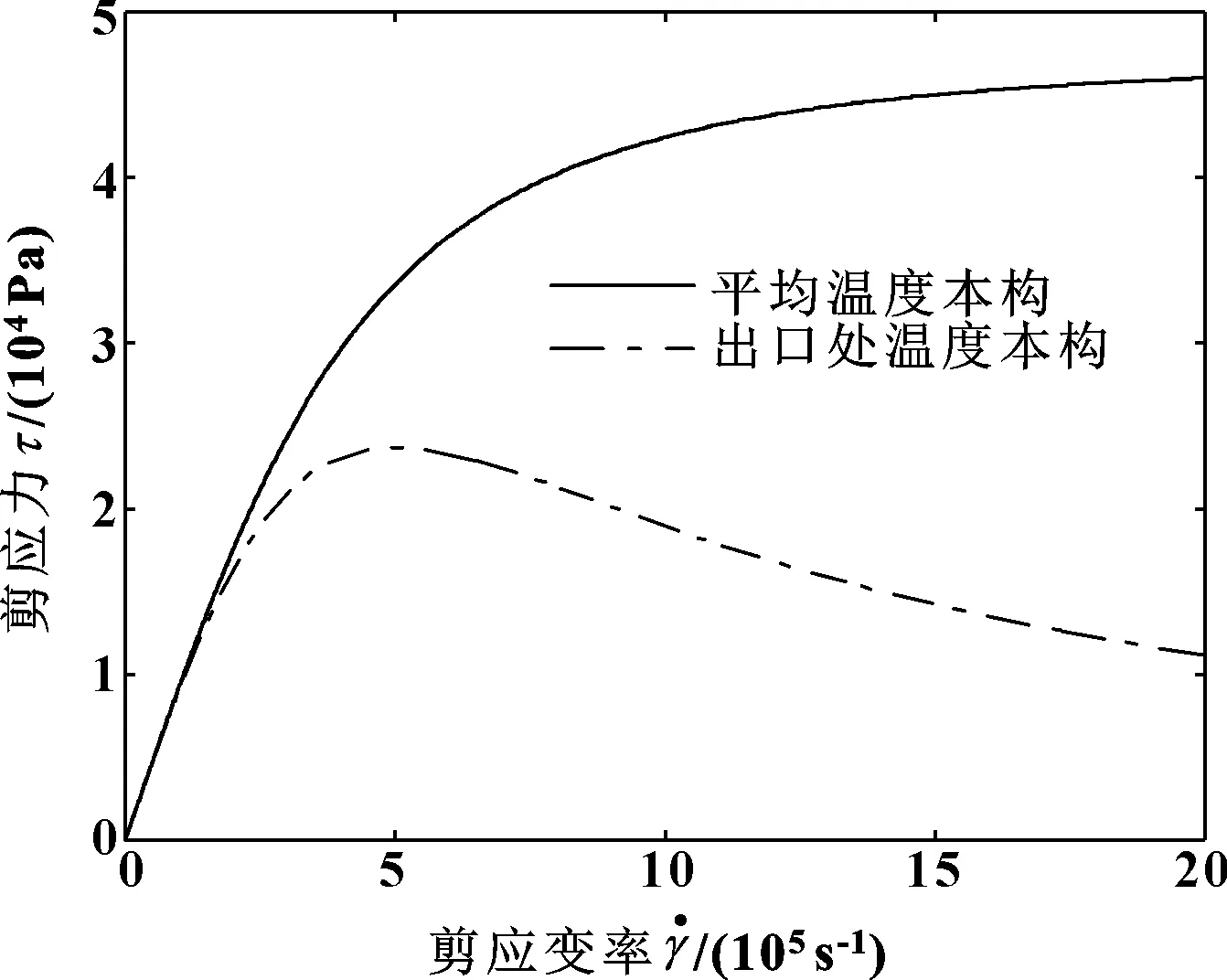
图7 平均温度本构曲线与出口处温度本构曲线

图7中出口处温度本构曲线在剪应变率为5×105s-1时，剪应力取得最大值23 714 Pa。

由图7可以看出，出口处温度本构曲线在剪应变率变化范围小于2×105s-1时，几乎与平均温度本构曲线重合，润滑液均表现为牛顿流体;在剪应变率大于2×105s-1之后，两条曲线变化趋势开始不同，出口处温度本构曲线所表现出的剪切稀化现象更加明显和剧烈，并在剪应变率为5×105s-1时，剪应力达到最大值。之后继续增加剪应变率，剪应力不再随之上升，反而开始下降。也就是说，在剪应变率高于5×105s-1这一极限值后，将会发生润滑失效现象。

3.3 不同位置温度本构曲线对比分析

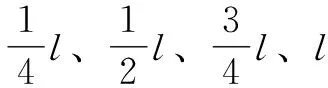
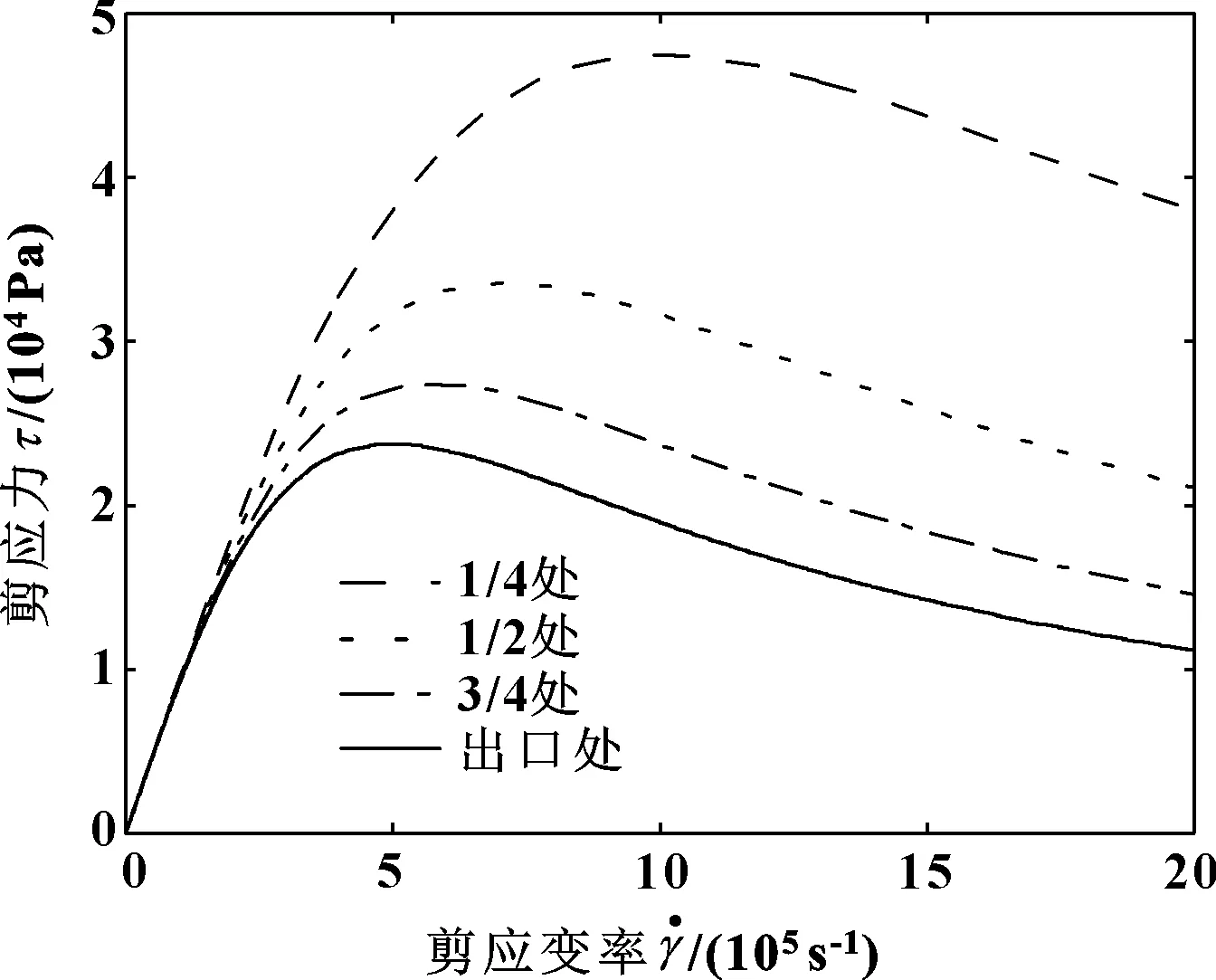
图8 不同位置的温度本构曲线

表2 不同位置剪应力极限值

由图8和表2可以看出，在整个润滑接触范围内，不同位置润滑液所能达到的剪应力极限是不同的，距离入口越远的地方，润滑液所能达到的剪应力极限越小，取得剪应力极限时对应的剪应变率值也越小。在出口处润滑液能达到的剪应力极限值最小，承载能力最低，这也印证了出口处是润滑接触区的最危险点。

4 讨论

长期以来人们就认识到了温度会引起润滑失效[16]。WINER[17]考察了温度对润滑剂的影响，通过大量实验证实在较高温度下润滑剂存在极限剪应力。HAN和PARANJPE[18]采用合理的边界条件分析了有限长径向滑动轴承中的温度分布，指出用平均温度表示的等黏度计算方法可以得到与实际情况相符的分析结果。由此可见，实际中经常存在温度引起的润滑失效现象,但是由于一直以来雷诺方程与能量方程都是分开求解，难以看出温度如何导致油膜承载能力下降，最终导致润滑失效。文中通过对能量方程的简化，采用变量消去的方法分析温度对承载能力的影响，解释了温度失效这种现象是如何发生的。从结果可以看出：高温区的尾部是承载能力变化最快的区域，该区域的承载能力上升趋势逐渐变得缓慢，之后开始下降，当这种下降超过膜厚下降带来的承载能力上升时，润滑失效开始发生。

5 结论

通过在一定的合理假设条件下求解简化的能量方程，得到了考虑温度效应的非牛顿流体本构方程，并分析温度引起的流体非牛顿特性变化。结果表明：

(1)采用接触区平均温度得到的温度本构方程，随着剪应变率的增加，润滑液首先表现为牛顿流体，之后出现剪切稀化现象，最终剪应力随着剪应变率的增大非常缓慢增大，整个过程可以一直保持有效润滑。

(2)采用接触区出口处温度得到的温度本构方程，随着剪变率的增加，润滑液同样首先表现为牛顿流体，之后出现剪切稀化现象。在剪应变率增大到一定程度时，剪应力会达到极限值。在此基础上继续增大剪应变率，剪应力不会随之增大，反而开始减小。即在达到剪应力极限后，继续增大剪应变率，将会出现润滑失效现象。

(3)对不同位置温度本构方程的分析表明，随着距离初始接触点距离的增大，润滑液的剪应力极限值逐渐减小。在整个润滑接触范围内，出口处润滑液能达到的剪应力极限值最小，印证了出口处为最危险点。