两种障碍距离变换栅格生成方法的对比分析

吴 凯 马艺文

(1. 济南市勘察测绘研究院, 山东 济南 250013; 2. 武汉市国土资源和规划信息中心, 湖北 武汉 430014)

0 引言

在现实世界中,两个目标物之间可以直接通行的情况较少,一般都需要绕过若干障碍物才可到达。地理空间问题中有很多典型的障碍空间问题,例如:军事问题中如何选择合适的进军路线以避开难以逾越的地理障碍及人为障碍[1];日常生活中交通工具绕开拥堵路段或施工路段的最短路径规划[2];灾害救援中“安全岛”问题[3];无人驾驶飞机的防撞避障和导航设计问题[4];科学研究中机器人避障路径规划问题[5];迷宫求解问题[6-7];障碍空间最近邻查询问题[8]。障碍空间,指空间中具有各种障碍物,此处的障碍物并非单指点或线或多边形,而是指全形态图形,它是点、线、面以及它们的组合,障碍本身不计算距离,并且不传递距离。

距离变换是计算并标识空间点(对参照体)距离的变换或过程。障碍距离变换,即在空间中存在障碍物时,距离的传播需要绕过障碍物,它属于条件距离变换[9-10]。这类问题比较抽象却来源于实际地理世界的需要,障碍距离变换是解决此类地理空间问题的有效途径。本文主要对比了两种障碍距离变换栅格生成方法,并进行了精度分析和对比。

1 障碍距离变换(DTO)

距离变换是将包含实体特征和空间背景两种像元的二值图像转变为距离图像的变换。在距离图像中,每一个像素值表示该像素到其最近的一个实体像素的距离,具体体现为每个实体的距离波不断地往外空间进行扩张,直到与邻近实体的距离波相遇。距离变换的结果往往是空间等距离线,任一点的趋源梯度线(即该线上任一点的切线方向都垂直于过该点的等距离线),即该点趋源的最短路径。

当考虑障碍空间问题时,上述距离变换则应扩展为DTO(Distance Transformation with Obstacles),即在障碍空间中进行距离变换。空间中有生成元还有若干障碍,生成元传播的距离波需要绕过障碍进行传播。由以上定义可知,一般意义上的距离变换可以看作是障碍物个数为零的障碍距离变换。

2 地图代数障碍距离变换算法(MA-DTO)

地图代数的障碍距离变换(MA-DTO)在二维障碍空间中是通过栅格路径距离变换实现的。可根据精度要求确定开窗大小,采用3×3,5×5等奇数(2n+1)×(2n+1)模板。模板栅格路径定义为模板的中心至其他各个栅格中心间的有限个方向线段的组合,模板栅格路径所对应的长度称为模板栅格路径长度。

3 ArcGIS障碍距离变换的实现方法(ArcGIS-DTO)

本文主要利用ArcGIS的成本距离(Cost Distance)工具,来计算每个像元到成本面上最近源的最小累计成本距离,即ArcGIS-DTO。在使用Cost Distance工具进行障碍距离变换时,生成元(Source Data)可以为矢量数据也可以为栅格数据,如果是栅格数据则具有 NoData 值的像元不包括在源集内,成本栅格数据(Cost Raster)中的NoData部分充当成本面中的障碍。

成本距离的算法如下:像元八邻域从像元0移动到四个与其边连接(1、3、5、7四像元)的近邻之一,取像元1时,跨越连接线移动到相邻结点的成本为a1=(cost0+cost1)/2,其中:cost0代表像元0的成本,cost1代表像元1的成本,a1为从像元0到像元1连接线的总成本。如果沿对角线移动,例如从像元0到像元8,则连接线上的行程成本为a2=1.414 214(cost0+cost8)/2,其中cost0代表像元0的成本,cost8代表像元8的成本,a2为从像元0到像元8连接线的总成本，如图1所示。

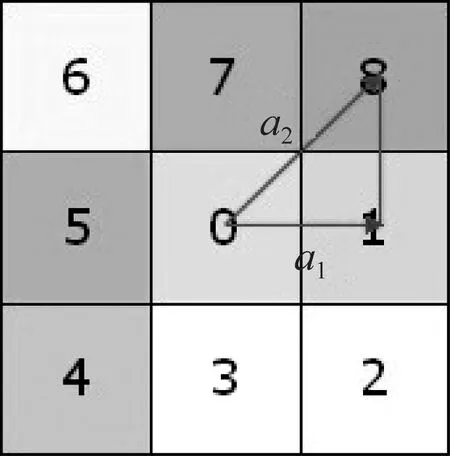
图1 像元八邻域

4 两种DTO算法的精度对比

4.1 理论分析

MA-DTO算法是一个统一的、通用的算法,具有优良的数据初始化、可视化性能,并且障碍物和发生元为全形态图。栅格空间下两定点之间的距离由其所属的两栅格中心间的距离定义。在障碍空间下由于连通概念的改变,障碍空间下的栅格路径定义为指定两定点a、b所属栅格中心间并由相通栅格中心间线段组成的有序线段集。栅格路径所对应的累计长度称为栅格路径长度。一般情况下,两定点之间的栅格路径并不唯一,往往有多条,所有路径中最短累计长度的栅格路径最有意义。实际上基于地图代数的距离变换给出了整个障碍空间所有点的趋源距离,并且给出了多生成元的整个障碍空间所有点的趋最近元距离。

ArcGIS-DTO的实现工具,成本加权距离通过将距离等同为成本因子来修改“欧氏”距离,该成本即为经过任何指定像元所需的成本。成本分配工具可以基于累积行程成本来识别最近(或成本最小的)源的像元。成本回溯链接工具将提供一个道路地图,用于标识从任何像元开始,沿着最小成本路径,返回到最近源的路径。

4.2 可视化对比

下面以一个点的距离变换为例,对比其距离波的形态,如图2所示,图2(a)为一个点的欧氏距离变换图,其产生的距离波为同心圆;图2(b)为ArcGIS中Cost Distance所使用的3×3模板距离变换,可以看出由于3×3模板的八邻域结构,生成的距离波是以等边八边形的方式逼近欧氏距离变换的圆形;图2(c)为地图代数方法一个点的距离变换结果,使用的是17×17模板,从距离波的形态上来看,已经十分精确地逼近欧氏距离变换结果。

图2 一个点的距离变换对比

用ArcGIS的距离变换结果叠加欧氏距离变换的同心圆,来观察ArcGIS实现结果的误差分布情况。如图3所示,为ArcGIS的3×3模板距离变换结果。

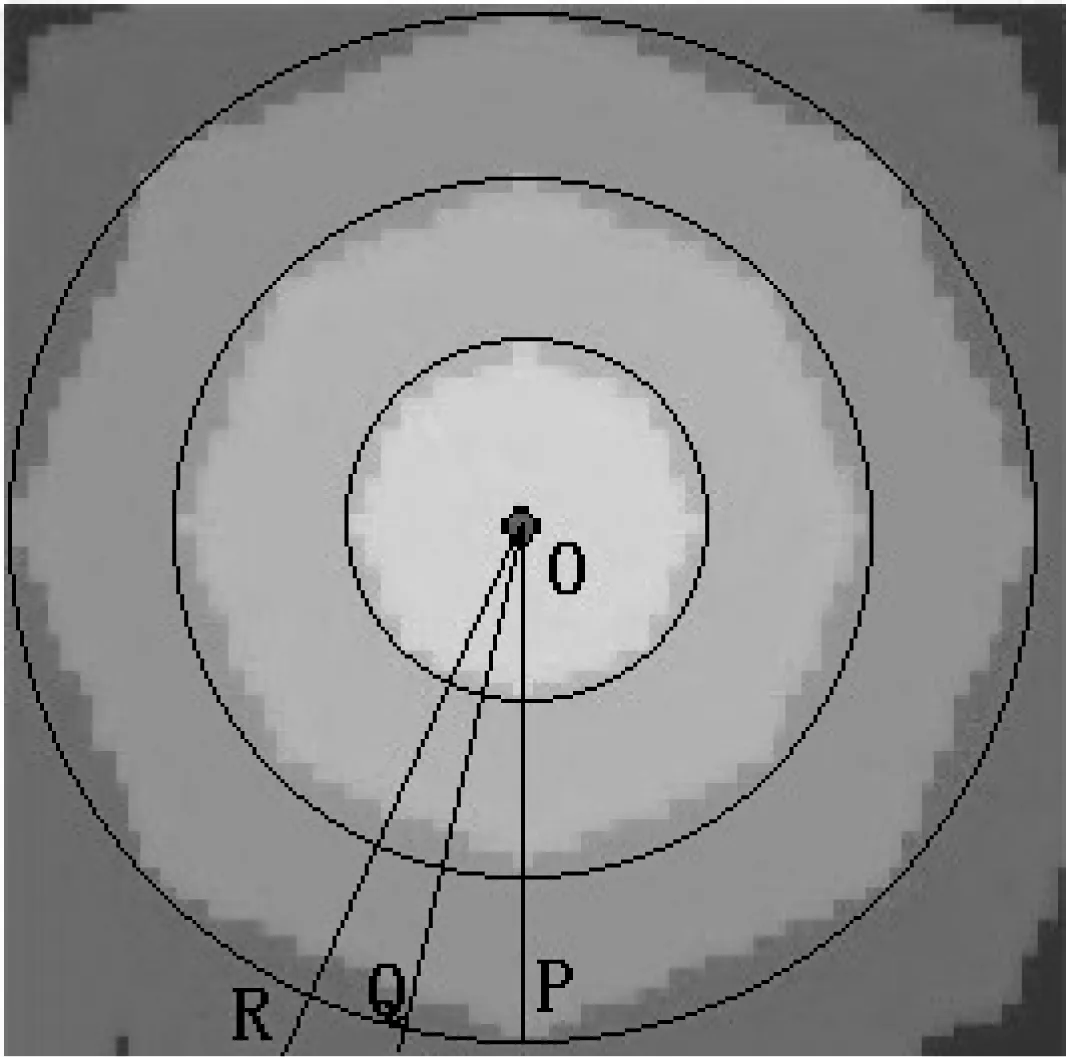
图3 误差分布示意图

叠加欧氏距离变换距离波同心圆可以看出,在八方向上,如线段OP所在位置,ArcGIS的结果和欧氏距离相等;在两个相邻八方向的中点,如线段OR所在位置,误差最大;误差随着向八方向的靠近而减小。设线段OP、OQ、OR所处位置处的误差分别为ΔOP、ΔOQ、ΔOR,则ΔOP<ΔOQ<ΔOR。

以线状生成元在障碍空间中的距离变换试验来进行两种DTO实现方法的精度对比,如图4所示,图4(a)中直线段生成元,螺旋区域内部为距离变换空间,外部为障碍空间;图4(b)为ArcGIS实现的DTO图;图4(d)为地图代数方法实现的DTO图。图4(c)和图4(e)分别为两种方法实现结果的局部放大图,放大部分为螺旋弯曲单元的转弯区域。对比图4(c)和4(e)可以看出:地图代数方法的距离波更平滑、更细腻,而ArcGIS的距离波在转弯区域容易形成折线,距离波纹不够平滑。

图4 线状生成元障碍距离变换精度对比

4.3 量化对比

如图5所示,图5(a)中点为生成元,共7个,线和面为障碍物;图5(b)为ArcGIS实现的多点生成元DTO图;图5(c)为地图代数方法实现的DTO图。两种方法所得距离波的形态不同之处前面已经进行了讨论。在此,布设距离变换图上n个随机点作为检查点,通过对比它们所在位置处两种距离变换结果的距离值,分析距离差值的变化规律。

图5 多点生成元DTO

在图幅范围内随机选取40个检查点,如图6所示,三角形点在此用P1,P2,…,P40来表示。图6(a)为检查点与ArcGIS-DTO结果的叠加图,图6(b)为检查点与MA-DTO结果的叠加图。

图6 随机点与DTO结果的叠加

采集40个检查点所在位置,ArcGIS-DTO和MA-DTO所得到的两个距离变换结果图中的距离值。如表1所示,D1为ArcGIS所得结果的距离值,D2为地图代数方法所得结果的距离值。再求出两种距离值的差值(ΔD),ΔD=D1-D2。对40个检查点按照距离值从小到大的顺序进行排序,排序后的结果如表2所示。

表1 随机点处距离值及距离差值 单位:m

表2 按距离值从小到大排序 单位:m

由于MA-DTO方法已十分接近于欧氏距离变换,所以本文将MA-DTO方法设为标准,考察ArcGIS-DTO的误差。则表2中距离差值ΔD可表示为ArcGIS-DTO的误差值。利用误差值(ΔD)和ArcGIS-DTO的距离值(D1)绘制成折线图,即误差随距离值变大的变化趋势图。如图7所示,图7(a)中的0值点即为上述的八方向上的点,在统计变化趋势前我们先将0值点去除,统计其余37个点的趋势图,如图7(b)所示。

图7 ArcGIS-DTO结果误差值随距离值的变化趋势图

对图7(b)所示的误差值随距离值的变化趋势图进行线性回归,如图8所示,线性回归函数为:

图8 误差随距离值变化趋势线性回归

y=1.926 54+0.062 38x(x为距离值,y为误差值),相关系数R=0.811 48。可以看出,虽然距离差值有波动,但整体上来讲,随着距离值的增大,也就是距离生成元越远,ArcGIS-DTO的误差越大。

5 结束语

通过可视化和量化两种方式的精度对比,本文得出以下结论:ArcGIS-DTO和MA-DTO在实现障碍空间的距离变换时都是模拟无障碍空间中欧氏距离变换的思想。地图代数算法使用的模板大小可以为3×3、5×5、奇数(2n+1)×(2n+1),随着n的增大误差会越来越小,越接近欧氏距离,精度也越高,但算法的复杂性也会增加;ArcGIS中使用的算法是固定的3×3模板,所以灵活性比较差,精度相对也较低些。