基于Mumford & Shah算法的Mark点图像修复研究

王业率，宋建华，何鹏，张龑

(湖北大学计算机与信息工程学院， 湖北 武汉 430062)

0 引言

随着电子半导体行业的不断发展，电子产品逐渐趋于小型化、精密化、高性能、高质量等特点，PCB板的制造工艺面临着巨大的提升需求.PCB板的制造流程中，曝光显影工艺环节需对PCB板位置进行高精度定位识别，进一步将定位位置发送至曝光设备进行曝光处理.而识别过程通常采用PCB板上Mark点完成.Mark点包括通孔、镭射曝光孔等多种形式，为方便简化后续工艺操作以及提高识别精度，PCB板通常较多采用通孔形式的圆形Mark点.

在实际生产过程中，在针对边缘有缺陷的圆孔时，常见算法在识别成功率以及识别精度存在提升空间，研究学者也做出大量工作.熊光洁等人针对Mark点的椭圆度提出了识别算法，采用Otsu’s算法对Mark点图像进行分割，然后实现坐标定位[1].乔闹生等人基于Hough变换提出图像边缘检测方法,该检测方法相对于具有一定算法优势[2].

此外，对覆有感光膜的圆孔进行图像采集时，会时常碰到感光膜反光现象，反光现象形成的反射光斑形状大小不固定.在机器视觉领域，可利用图像修复的方法将Mark点区域的反射光斑进行去除、修复.常见的图像修复算法目前包括三类：一类是基于偏微分方程(PDE)的数字图像修补技术；第二类是基于纹理合成(TS)的图像修复技术；第三类是基于稀疏表示(SR)方法的图像修复技术. 此外，FMM算法通过领域图像加权处理的方式进行修复，修复速度较快，修复效果较好，但是在边缘细节具有缺陷[3,4].

偏微分方程算法最早由Bertalmio等人提出BSCB算法，根据等照度线方向将完好区域图像信息延伸至待修复区域[5]， BSCB算法计算复杂度较高. Bertalmio等人对图像修复做出了大量研究，将流体力学中的Navier-Stokes模型(N-S模型)应用到图像修复算法中，图像边缘部分存在缺陷[6,7].

Mumford 以及 Shah提出了基于体积能量的Mumford & Shah算法(M&S算法)模型[8]. 针对该泛函中存在的复杂度问题，Ambrosio及Tortorelli使用椭圆形对泛函进行了逼近，且使用Euler-Lagrange方程及有限差分法降低计算复杂度[9,10]. 该算法在去除脉冲噪声较BSCB算法及Navier-Stokes算法具有一定优势，且降低了计算复杂度，同时在边缘细节处理方面也较FMM算法更优. 在具有长条状反光光斑的图像场景下，Mumford & Shah算法对于大块区域修复效果不佳的特点得以避免.

1 算法原理

1.1 Mumford & Shah泛函模型Mumford & Shah提出的图像修复模型是以最小化能量泛函为基础的，该能量泛函可以表示为[9]：

F[u|u0,I]

(1)

其中，I表示修复图像区域，u0表示图像的可用部分，可表示为加入高斯白噪声的图像.

根据贝叶斯原理，该泛函可进一步表示为数据模型部分与图像模型部分的和：

(2)

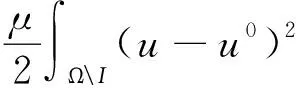
Mumford & Shah的图像分割理论将E[u]进一步表示为：

(3)

B 表示图像的边缘部分，并用一维Hausdoff 测度进行度量.因此，Mumford & Shah模型可表示为：

(4)

1.2 Ambrosio & Tortorelli改进模型Ambrosio & Tortorelli将原Mumford & Shah模型用椭圆泛函进行了简化，提高了收敛速度. 其做出的改进包括[10]：

(5)

(6)

χ为边缘部分的过渡区域.由此，修复问题可演化为求解最小化问题：

(7)

该最小化问题的求解过程主要包含u和χ的积分计算，使用有限差分法进行求解的过程较为简洁.

分别定义算子Lχ和算子Mu：

(8)

(9)

Euler-Lagrange方程可表示为：

(10)

Muχ=1

(11)

2 Mark点图像修复算法

2.1 Mark点图像PCB板生产过程中的Mark点定位工序通常需要将感光膜贴附在PCB板上.当PCB板上已附有铜箔图案时，铜箔图案在图案边缘区域部分具有落差，落差深度与腐蚀程度一致.感光膜通常厚度在0.3 mm以内，经压膜工艺处理时表面易产生形变，从而导致环形光源光线从感光膜反射至工业相机镜头处形成反射光斑，如图1所示.

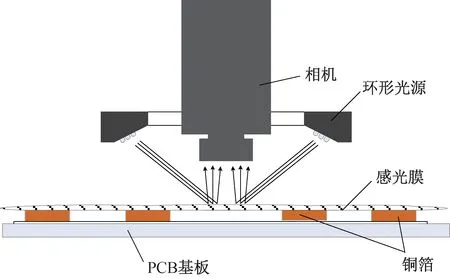
图1 PCB板机器视觉系统光源反射示意图

此应用视觉系统成像距离较短，且对清晰度要求较高，同轴光源在设计需求上存在缺陷，因此多采用环形光源作为光源方案.环形光源倾斜角的存在导致光源光线经过漫反射后易进入工业相机取景范围，从而在Mark点采样图像中形成光斑.

常见的最小二乘法、霍夫变换等圆拟合算法在干扰图形区域面积过大、干扰图形边缘距离圆弧距离过大等状况下，存在误差较大问题.待图像转移PCB板紧密吸附在曝光设备黑色台面上，Mark点通孔处图像灰度与台面保持一致，反射光斑区域图像灰度与光源保持一致.因此，在依赖灰度阈值作为轮廓化处理前提下，反射光斑、非通孔区域与通孔区域的边缘易形成较大灰度差，从而误识别为轮廓，如图2所示.

图2 含反射光斑区域Mark点图像轮廓化示意图

2.2 算法步骤本算法的具体步骤如下：

Step1：使用Otsu’s算法对图像生成蒙版图像.

Step2：初始化参数读入待修复图像和蒙版图像.

Step3： 在Euler-Lagrange方程边界条件确定情况下，定义微分算子Lχ及Mu.

Step4：采用算子Mu求解Euler-Lagrange方程中χ，更新迭代项χ.

Step5：采用算子Lχ求解Euler-Lagrange方程中u，更新迭代项u.

Step6：计算迭代项u与前值的差值.如果经迭代的图像u与前次迭代图像u之差小于预定阈值threshold_value，迭代结束；否则回到Step4继续进行迭代.

Step7：输出经修复的图像.

3 实验分析

基于前述理论算法，对进行了修复实验.实验所使用计算机配置包括： CPU为Intel酷睿i7-9700 3.0 GHz，内存为16 GB，算法用MATLAB R2018a进行实现.在本算法的实现过程中，令图像区域为Ω∈(0,1)×(0,1),迭代次数iter取20次，迭代误差阈值tol=1e-14.Ambrosio-Tortorelli模型逼近精度epsilon=0.05.

以PCB板上mark点通孔为实验对象，尝试对Mark点图像进行修复实验.Mark点图像大小为696×520像素，如图3(a)所示，图中Mark点通孔在方形铜箔图案中，感光膜由于压制不工整而产生褶皱，导致反光光斑产生.此类反光光斑图案为条状，条状区域宽度不一，以便针对不同情形下图像特征进行修复.使用Otsu’s算法对图像进行阈值分割，阈值参数为0.7，分割后光斑区域即图3(a)中噪点区域.由Otsu’s算法分割出的mask蒙版如图3(b)所示.经本算法修复后，图像中通孔内部光斑区域得到较好的修复，通孔边缘毛刺较少；铜箔图案处光斑区域出现了涂抹痕迹，显示该算法在具有大量纹路区域处缺乏修正，修复图像如图3(c)所示.

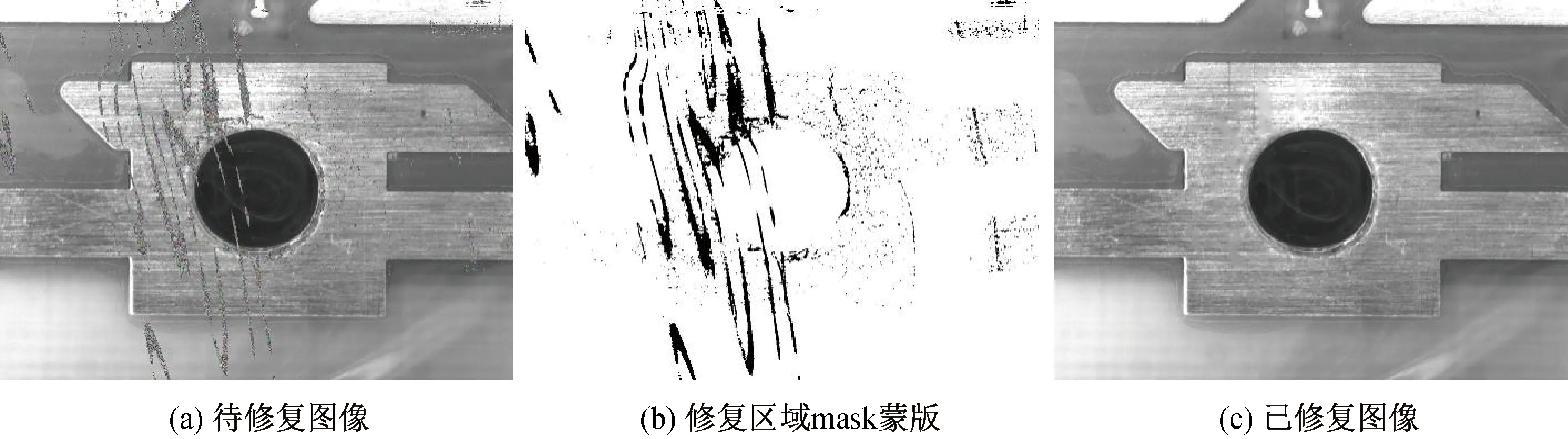
图3 Mark点修复结果

为检测噪声环境对图像修复的影响，特对待修复图片加入噪声进行修复实验，图片大小缩放为279×208像素.由于椒盐噪声能够体现出脉冲干扰性质的图像畸变，因此在待修复图像中加入噪声密度参数为0、0.01、0.05、0.1、0.5的椒盐噪声，以未加噪声情况下修复图片作为基准，采用MSE、PSNR、修复时间作为客观评价指标对基准图片进行修复效果评估，修复结果见表1. 添加的噪声对该修复算法影响较小，在噪声密度达到0.5时，PSNR仍然可达33.411，且修复时间随噪声密度增加的变化不大.

分别采用Mumford & Shah算法、BSCB算法、Navier-Stokes算法、FMM算法对图3所示图形进行对比修复实验，图片大小为279×208像素，取通孔左上角附近区域以及无铜箔区域作为实验一与实验二的实验对象进行修复实验，修复结果如图4及图5所示.

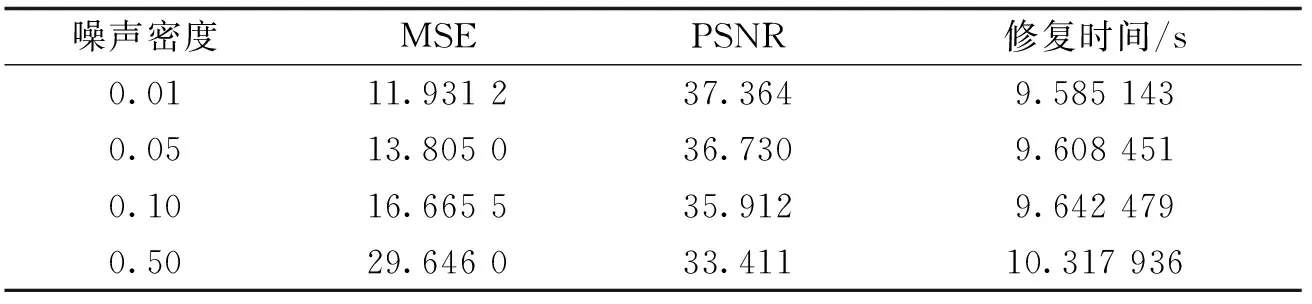
表1 不同椒盐噪声密度下的修复数据

图4 实验一修复结果

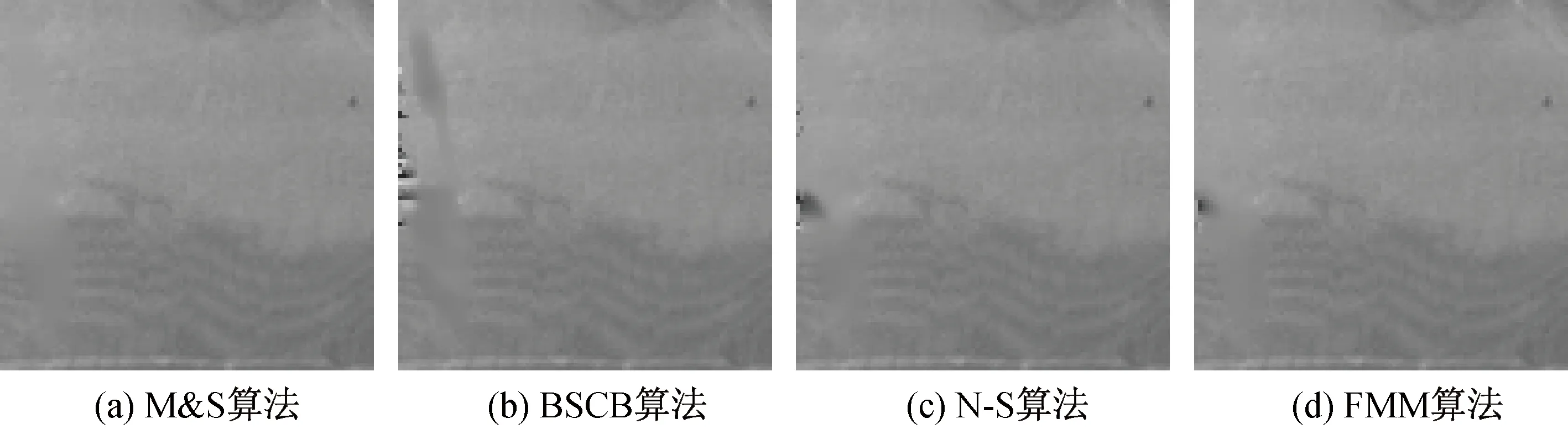
图5 实验二修复结果

本研究采用的Mumford & Shah算法能够对面积较小的反光区域进行有效修复，面积较大的修复区域图像细节较少；BSCB算法同样对细节有较好修复效果，但是在面积较大的修复区域修复效果不满意，图像中出现了修复过程产生的噪点；Navier-Stokes算法由边界向内进行修复，在修复区域边缘较平滑，但是在内部区域存在分块痕迹；FMM算法修复细节较丰富，在通孔边缘处仍存在毛刺状修复痕迹，实验二中细节部分出现了轻微噪点.

对实验一及实验二提取客观评估指标MSE、PSNR进行评估，MSE值越小，PSNR的值越大，说明修复效果越好，修复结果见表2. 通过实验结果可见，Mumford & Shah算法修复的效果最佳，体现了该算法对于此类条状修复对象的较佳适应性.

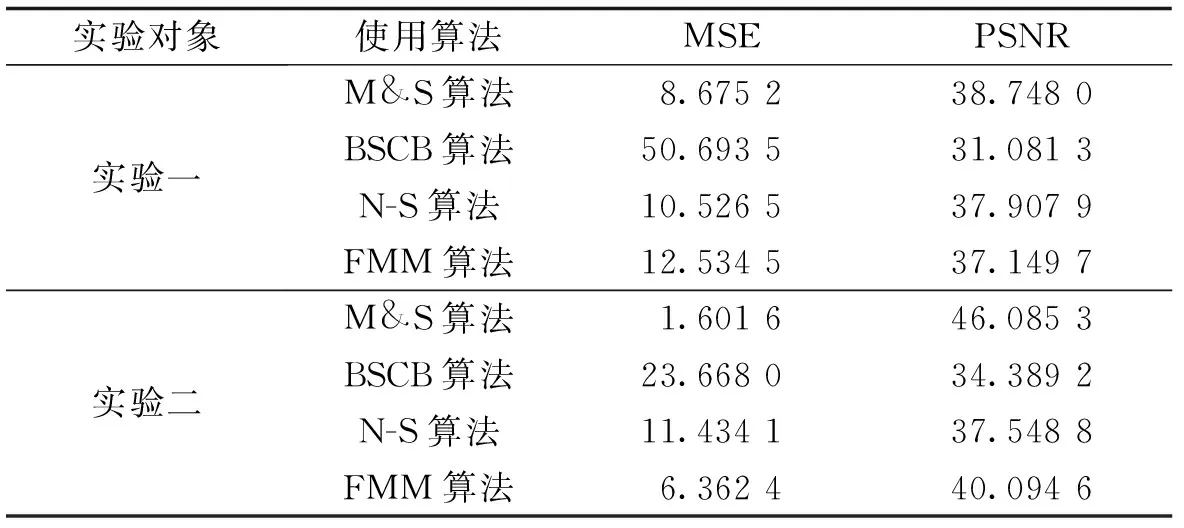
表2 使用不同修复算法的实验数据对比

4 结语

PCB板的曝光工艺是其生产线产能的瓶颈，而Mark点识别失败是曝光工艺环节停产的重要因素之一.现有的机器视觉算法在常见的异形孔识别成功率上尚存在提升空间，对异形孔之上反射光斑的修复处理将提高PCB板产能.

本研究采用Mumford & Shah算法对Mark点图像进行了修复处理.由于反射光斑显长条形的形状特征，且灰度上与通孔区域形成反差对比，因此，在边缘区域的修复效果较好.然而，该算法对于部分较大面积反射光斑的修复效果尚存在优化空间.后续可以对算法进行改进优化，或者使用深度学习方式对光斑区域进行识别、修复，以提高识别成功率以及精度.