剪弯梁宏细观多尺度非线性有限元分析
胡 彪,王宪杰,2,3,王思文,李承玥,王兆毅,翁振江
(1.云南大学建筑与规划学院,昆明 650500;2.浙江大学建筑与工程学院,杭州 310058;3.浙江东南网架集团有限公司,杭州 311209)
0 引 言
混凝土的多尺度研究,有利于充分了解其损伤机理[1]、非线性行为[2]、动力响应[3]、可靠度[4]等。混凝土宏观非线性力学行为及尺寸效应源于其细观非均质性[5],其内部粗骨料、细骨料、水泥等材料及孔隙裂缝的不均匀分布导致了这种细观的非均质性。
近年来,国内外学者从多个角度研究了混凝土细微观结构变化对宏观构件性能机理的影响。金浏等[6-8]从细观角度出发,提出了反映尺寸效应的混凝土力学性质的修正公式,并进行了数值模拟和论证。Escoda等[9]研究了骨料形状对混凝土有效剪切模量和有效体积模量的影响,指出当骨料力学性能与周围的水泥砂浆相差较大时,骨料形状对局部应力场有较大的影响。许文祥等[10]以椭圆形骨料为依托,分析了骨料的最大粒径和面积占比对混凝土边界效应的作用。以上相关研究一致认为,骨料粒径、形状及其分布对宏观力学性能起着至关重要的作用。王飞阳等[11]采用一致多尺度方法对混凝土结构模拟得到了带裂缝服役三点弯梁在不同裂缝深度条件下的弯矩-挠度曲线。Bin等[12]通过对混凝土非关键区、关键区、损伤区采用不同单元尺寸和理论建立了三级模型,模拟了在地震作用下细观损伤到结构破坏的跨尺度过程。Huang等[13]基于原位X射线得到了混凝土试样的电子计算机断层扫描(CT)图像,将二维模型自下向上叠加生成三维模型,并模拟试件拉伸断裂行为。然而,以上混凝土损伤研究主要集中于断裂现象与宏观力学行为关系的探究,并未考虑细观骨料级配中最大粒径的变化对宏观构件裂缝展开的影响。
为揭示混凝土尺度相关性与材料非线性损伤关系,本文通过生成多组符合Fuller级配的等面积占比细观骨料模型,选用不同的最大粒径,依据等效化理论求出混凝土细观单元等效化参数,并通过均匀化方法建立混凝土宏细观跨尺度关联。在此基础上建立混凝土宏观梁构件,模拟其在受力作用下的裂缝开展及损伤情况,使得混凝土细观层面上的变化在宏观力学性能上得到体现。
1 细观骨料级配生成
1.1 细观骨料Fuller级配
为使生成的混凝土模型具有较好的密实度和宏观强度,选用Fuller级配曲线确定其骨料粒径[5]。考虑实际工程中使用骨料的最小粒径,潘子超等[14]将Fuller级配下骨料质量累积分布函数表达式改写为:
P3M(D)=Dn-DnminDnmax-Dnmin
(1)
式中:P3M(D)为小于指定粒径Di的骨料占所有骨料的质量分数;D为选用的目标骨料粒径;Dmax为骨料最大粒径;Dmin为骨料最小粒径;n为与颗粒形状特性相关的指数,常取0.45~0.7。
基于式(1)推导得到骨料粒径公式:
D=[P3M(D)·(Dnmax-Dnmin)+Dnmin]1/n
(2)
显然当已知骨料最大、最小粒径时,通过唯一确定随机变量P3M(D)即可求得符合Fuller级配的骨料直径D。
1.2 多边形骨料生成
已有科研成果中部分二维细观模型骨料为椭圆形或者圆形,相关模型比较贴合卵石骨料的截面形状,但实际工程中碎石骨料的使用更为普遍。因此本文拟生成边数为4~12的凸多边形碎石骨料模型[15]。建模过程如图1所示,基本步骤为:
(1)在目标区域内随机生成直径符合式(2)的圆形,并确定圆心坐标。
(2)随机生成4~12的一个数字记为m,以圆心为极点,横坐标方向为极轴,随机生成m个值为0°~360°的角度,按从小到大顺序排列并记为θ1,θ2,…,θm,分别计算:
xi=Dcosθi2
(3)
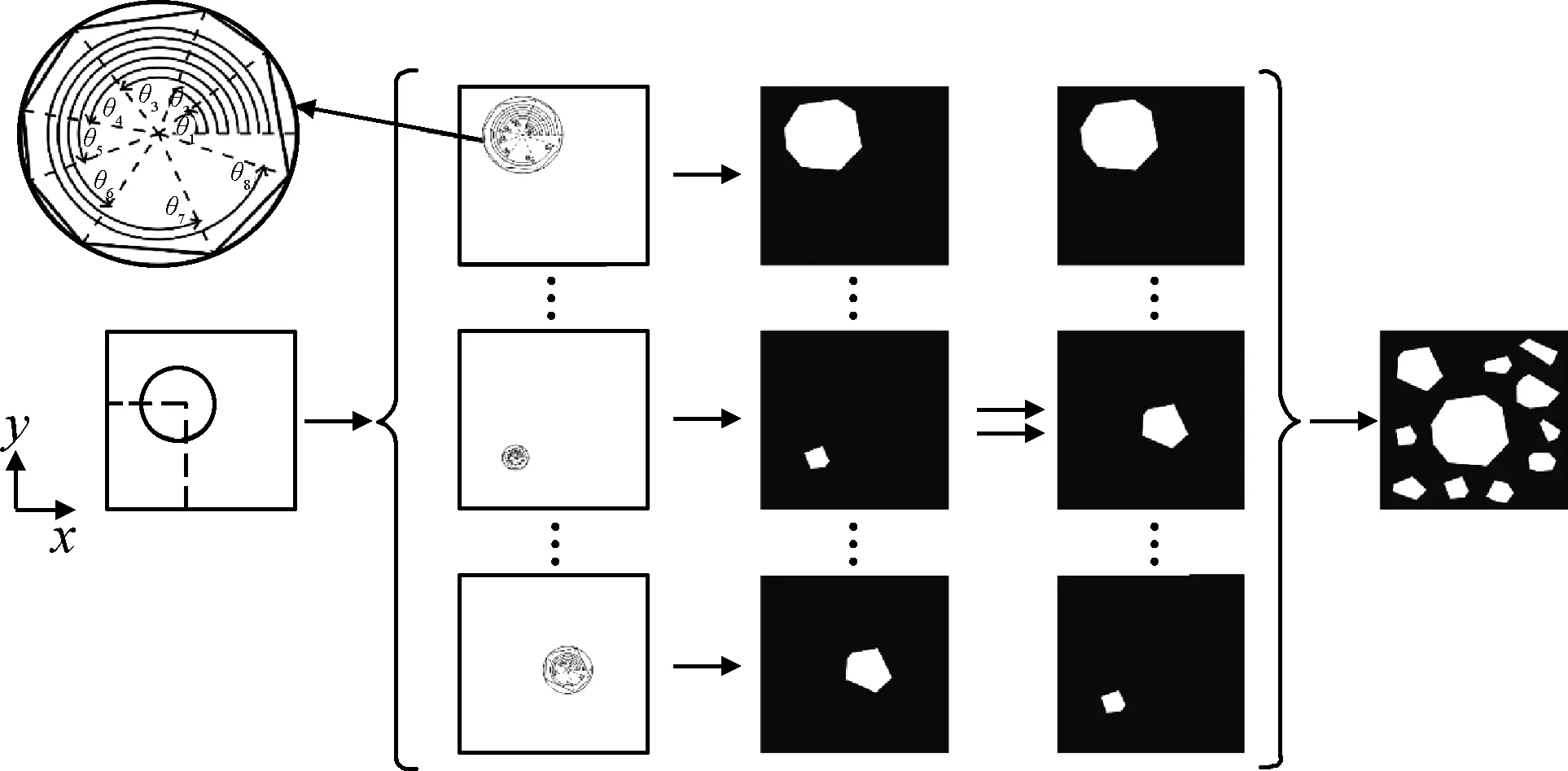
图1 多边形骨料模型生成过程Fig.1 Generation process of polygon aggregate model
(4)
式中:i为1~m之间的整数;xi、yi分别为多边形上第i个顶点的横坐标值和纵坐标值,得到m组坐标(xi,yi),并将其依次连接,得到符合预期的多边形。
(3)对多边形内部上色,计算多边形面积。
(4)重复步骤(1)~(3),直至生成的多边形总面积达到限值要求,并记录多边形总数。
(5)将多边形按面积从大到小排列,依次放置于目标区域内,通过识别放置位置像素的RGB(红绿蓝)值判断多边形是否重合,例如白色RGB值为(255,255,255),黑色RGB值为(0,0,0),比较RGB值,即可判断此处材料情况。
(6)导出生成的多边形模型。
2 细观-宏观跨尺度关联
2.1 等效化思想
考虑骨料在单胞内随机分布,为准确反映单胞内各个位置的性质,将单胞内部进一步划分为多个单元,在确保计算效率的条件下,尽可能划分更多的单元以提高计算精度[5]。同样采用像素色彩RGB识别方法,计算单元中骨料和砂浆的面积占比,求得每个单元的平均弹性模量和泊松比,并在有限元模型对应位置赋予相应的材料属性,再运用均匀化理论进行求解。模型等效化过程如图2所示。

图2 多边形骨料模型等效化过程Fig.2 Equivalent process of polygonal aggregate model
2.2 均匀化理论
均匀化理论以严格的数学推导为基础建立了从材料细观组成特性到宏观性质的联系[16-18],它假定材料的细观单胞结构具有空间周期性,利用单胞具备简化复合材料等效性能分析的能力[19],将宏观尺度上一点的位移、应力等物理量展开为与细观结构尺度相关的摄动量的渐近级数[20]。在二维弹性问题中,进一步引入单胞的静力平衡方程、几何方程和物理方程,并结合应力边界条件和位移边界条件,以此求得宏观结构的等效弹性参数。基于均匀化理论对生成的混凝土二维细观模型进行分析:首先由骨料最大粒径确定单胞内划分小单元的最大尺寸[20];其次计算每个小单元内的等效化力学参数;再次通过有限元软件分别求解单胞在单位横向、纵向、剪切应变及对应边界条件下的位移场;最后带入式(5)得到该模型的等效弹性模量矩阵,由此构建跨尺度关联。
EH=1|Y|∫Y(E-ETBχ)dY
(5)
式中:EH、E、ET分别为等效弹性模量矩阵、弹性模量矩阵和弹性模量矩阵的转置矩阵;Y为周期;B为节点位移向量至应变向量的变换矩阵;χ为位移场。
3 宏观混凝土损伤分析
3.1 混凝土本构关系
在确定混凝土细观结构规律和实现跨尺度关联的基础上,建立相应的宏观模型有助于理解其力学行为。为使模拟贴近实际工程中的表现,将细观模型所推导的等效力学参数带入混凝土受压、受拉力学性能统一计算方法[21-22]确定本构关系。相关公式及计算步骤为:
近似取受拉弹性模量(Et)与受压弹性模量(Ec)相等,并反推导混凝土立方体抗压强度可得:
fcu=(Ec9 500)3=(Et9 500)3
(6)
单轴抗拉、抗压强度统一计算式:
ft=0.24f2/3cu
(7)
fc=0.76fcu
(8)
单轴抗拉、抗压峰值应变统一计算式:
εtp=67f1/2t×10-6
(9)
εcp=520f1/3c×10-6
(10)
受压应力-应变曲线公式为:
yc=Acxc-x2c1+(Ac-2)xc, (xc≤1)
(11)
yc=xcαc(xc-1)2+xc, (xc>1)
(12)
受拉应力-应变曲线公式为:
yt=Atxt-x2t1+(At-2)xt, (xt≤1)
(13)
yt=xtαt(xt-1)1.7+xt, (xt>1)
(14)
式中:xc、yc、Ac、αc分别为受压应力-应变曲线的横坐标、纵坐标、上升段参数、下降段参数,分别满足xc=ε/εcp、yc=σc/fc、Ac=9.1f-4/9cu、αc=2.5×10-5f3cu;xt、yt、At、αt分别为受拉应力-应变曲线的横坐标、纵坐标、上升段参数、下降段参数,分别满足xt=ε/εtp、yt=σt/ft、At=Etεtp/ft、αt=1+3.4f2cu×10-4;ft、fc分别为混凝土单轴抗拉、抗压强度;εtp、εcp分别为混凝土单轴受拉、受压峰值应变;fcu为混凝土立方体抗压强度。
3.2 损伤因子
混凝土构件在服役过程中产生的裂缝会导致其性能的改变,为描述卸载时材料的刚度退化现象,将损伤因子带入混凝土本构关系[23],用于构件进入非线性阶段后的裂缝展开分析。
未受损材料弹性余能Wε0:
Wε0=σ22E0
(15)
受损材料等效弹性余能Wεd:
Wεd=22Ed
(16)
=σ1-d
(17)
式中:E0为材料未受损弹性模量;Ed为材料受损后弹性模量;d为损伤因子。
根据Sidoroff[24]的能量等价原理,因应力作用在受损材料和未受损材料上所产生的弹性余能具有相同的表达形式,所以可将应力替换为有效应力,或是将弹性模量替换为损伤时的弹性模量,即通过式(15)~(17)可求得材料应力(σ)应变(ε)与损伤因子(d)的关系式:
d=1-σεE0
(18)
将式(11)~(14)所求得混凝土材料在受拉、受压不同阶段下的应力应变关系带入式(18)中即可计算相应情况的损伤因子。
大多数民办高校教工党支部的组织生活仍然停留于传达上级的有关精神内容和完成上级的有关布置任务,组织生活活动方法陈旧或形式化,内容单一,缺乏创新意识,在民主生活会上的批评和自我批评时常流于形式而难出实际效果,这些都在一定程度上削弱了教工党支部的政治影响力。
4 算 例
4.1 细观骨料模型
本文建立了4组不同级配的混凝土二维细观模型,单胞尺寸均为300 mm×300 mm,每组均生成20个样本,骨料面积占比为40.00%~40.50%,混凝土中骨料和砂浆的材料参数按文献[25]选用,如表1所示。选取每组中较有代表性的细观模型如图3所示,组别编号1~4分别表示骨料级配为5~30 mm、5~40 mm、5~50 mm、5~60 mm。

表1 混凝土二相材料参数Table 1 Two-phase material parameters of concrete

图3 1~4组骨料级配细观模型Fig.3 No.1 to No.4 of aggregate grading mesoscopic model
处理1组细观模型并求解损伤因子的相关步骤为:
(1)对每个模型进行等效化处理,均划分成2 500个6 mm×6 mm的小单元;
(2)基于均匀化理论求得每个模型样本的等效弹性模量,并取平均值作为该组的弹性模量;
(3)将弹性模量带入式(6)计算混凝土立方体抗压强度;
(4)将混凝土立方体抗压强度带入式(7)~(10)求得混凝土单轴抗拉、抗压强度和峰值应变;
(5)取材料的四分之一峰值应变作为其进入塑性阶段后的应变增量,由式(11)~(14)求解相应的应力;
(6)将多对应变应力带入式(18)得到对应的损伤因子。
经上述步骤计算得到各组的数据,第一组结果如表2所示(因篇幅有限,取前10个数据)。各组抗压强度与受压损伤因子如图4所示,抗拉强度与受拉损伤因子关系如图5所示(选取具有代表性的10个点)。不难看出在混凝土进入塑性阶段之前,骨料最大粒径越小,抗压、抗拉强度越大;进入塑性阶段后,若达到相同的损伤因子,骨料最大粒径越小,所能承受的拉应力、压应力越大,即抗拉、抗压能力越强。观察不同骨料级配的差值变化可知,组别间抗拉强度的差值会随着损伤因子的增大而逐渐减小,抗拉强度降低至同一水平值;而组别间抗压强度的差值随损伤因子的增大,在达到极限抗压强度之前逐渐增大,在达到极限抗压强度之后,逐渐减小,抗压强度降低至同一水平值。

表2 混凝土计算参数Table 2 Concrete calculation parameters
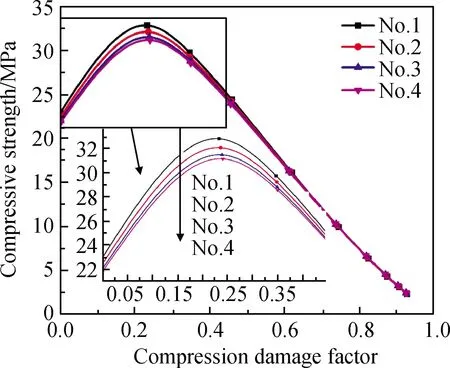
图4 抗压强度-受压损伤因子曲线Fig.4 Curves of compressive strength and compression damage factor

图5 抗拉强度-受拉损伤因子曲线Fig.5 Curves of tensile strength and strain damage factor
4.2 宏观剪弯梁模型
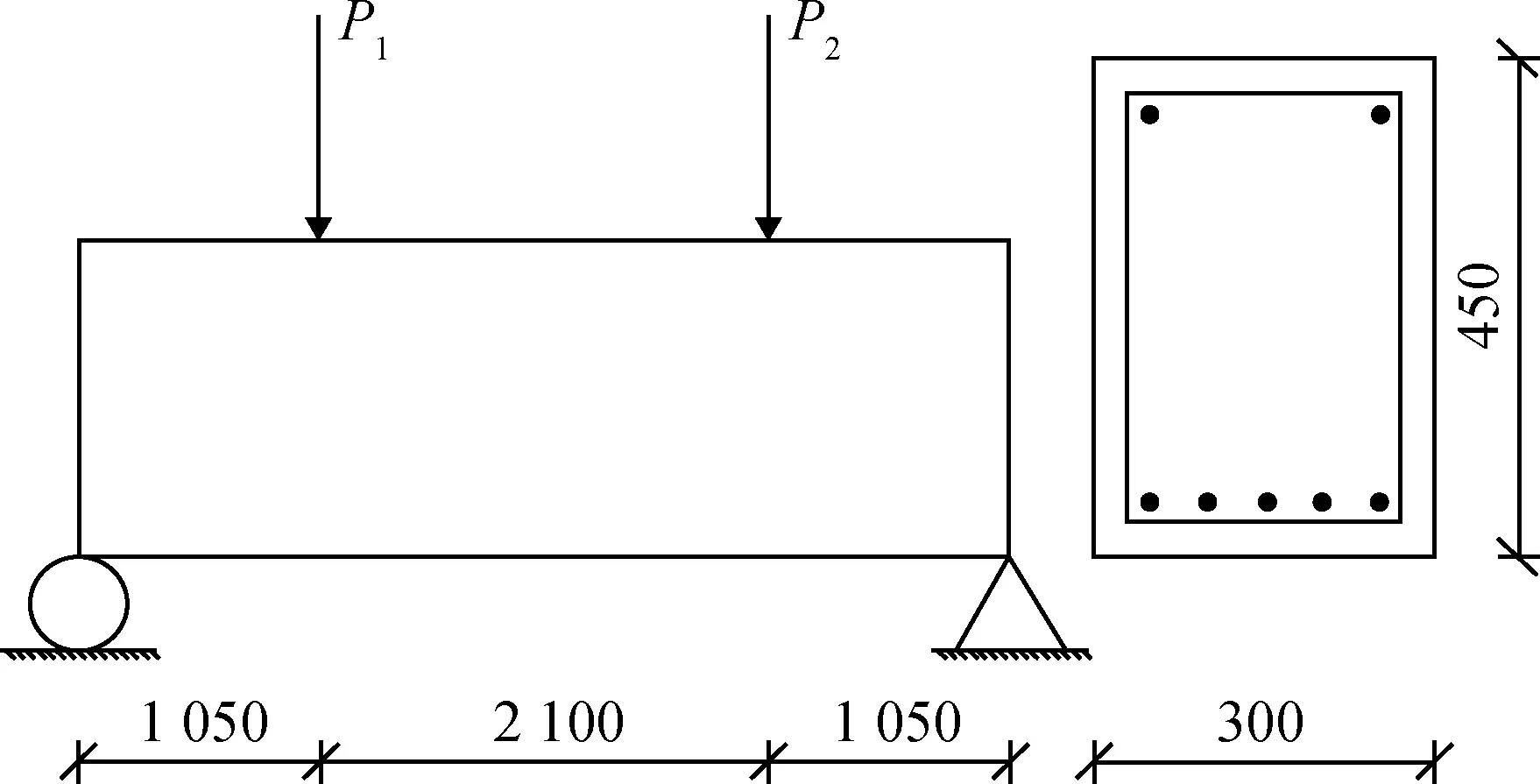
图6 剪弯梁计算简图(单位:mm)Fig.6 Calculation diagram of shear-flexural beam (unit: mm)

从图7中可以看出,每根梁中同时存在由弯矩引起的竖向裂缝和剪力引起的斜向裂缝,因梁在集中荷载作用点附近同时受到剪力和较大弯矩的影响,扩展最深裂缝均位于此处的弯剪斜裂缝,且裂缝整体分布较为对称,符合在两点集中荷载作用下,剪弯梁上剪力及弯矩的分布规律。
4根梁中,1号梁两侧斜向裂缝和跨中竖向裂缝发展最为明显,且裂缝分布范围最广,较长裂缝(超过截面高度40%的裂缝,下同)条数为17,但最大塑性应变值最小,为8.333×10-3,出现在集中荷载附近竖向裂缝的底部,呈现出正截面适筋破坏特征。2~4号梁中裂缝分布范围无明显差别,两侧斜向裂缝的延伸依次增强,较长裂缝条数依次为16、14、14,最大塑性应变值均出现在弯剪斜裂缝的中部,分别为1.114×10-2、1.147×10-2、1.222×10-2,呈现出斜截面剪压破坏特征,较1号梁脆性更为明显。

图7 剪弯梁最大塑性应变云图Fig.7 Maximum plastic strain diagram of shear-flexural beam
进一步分析模拟结果可知,在一定范围内选用的骨料最大粒径越大,混凝土梁构件出现较长裂缝条数越少,梁跨中部裂缝整体扩展深度越浅,即消耗应变能的能力越弱,因而导致最大塑性应变值越大。
5 结 论
(1)混凝土二维随机多边形骨料细观模型满足骨料面积占比相同且骨料级配均符合Fuller级配的条件时,在本文模拟尺寸范围内,混凝土骨料最大粒径越小,抗拉、抗压强度越大。不同骨料级配间抗拉强度的差值在进入塑性阶段后逐渐减小,而抗压强度的差值在达到极限抗压强度之前逐渐增大,在达到极限抗压强度之后,逐渐减小。
(2)宏观混凝土梁相同几何尺寸、钢筋配比和加载下,在本文模拟尺寸范围内,选用的混凝土骨料最大粒径越小,较长裂缝条数越多,最大塑性应变值越小,抗弯能力越强。
(3)混凝土梁构件选用的骨料级配最大粒径不同,有可能导致延性破坏向脆性破坏转变,即造成破坏模式发生根本性的变化,因此在施工过程中,严格控制骨料级配尤为重要。

