发电机螺栓松动故障特征检测方法及试验研究

李佳桐，张 跃，符栋梁，章 艺

（中船重工集团公司 第704研究所，上海200031）

电机与基础面存在接触刚度和接触阻尼，螺栓松动会对电机的振动特性产生很大的影响[1-2]，松动的螺栓会引发电机振动故障，威胁电机安全运行。由此，有必要研究螺栓松动特性与振动响应之间的内在联系，对系统的振动情况进行故障诊断。常用的故障诊断方法有解析冗余、神经网络、多元统计等，由于神经网络学习量大，收敛速度慢，不利于在线学习与诊断；解析冗余诊断结果受模型准确性限制，一旦出现外界干扰可能发生判断错误，本文利用系统的历史运行数据，来提取系统测量数据之间的内在相关性，选用主成分分析法将测量数据投影到残差子空间中，通过对比样本的平方预测误差与置信限，实现对螺栓松动的故障诊断[3]。

1 螺栓松动的故障特征诊断

1.1 基于EMD的信号处理方法

当大型旋转机械出现故障或负荷、转速发生变化时，其振动信号表现为时变的非稳定信号，为了正确地描述这类非线性、非平稳信号，提取典型故障特征，本文采用经验模态分解方法（Empirical Mode Decomposition，EMD）对故障信号进行处理，将其分解为若干个本征模式分量函数（intrinsic mode function，IMF）[4]。

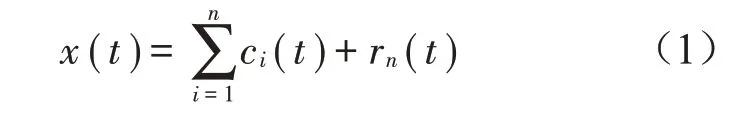
利用前5个分量提取特征[c1(t),c1(t),…,c5(t)]，这些IMF包括不同的频率分量。

1.2 主成分分析法

时域特征是信号特征的重要指标，通常分为维数指标和无量纲指标。尺寸指标对信号特性敏感，但在改变工况时缺陷不稳定，而无量纲指数可以排除这些干扰，具有较好的故障识别特性[5]，因此从原始数据和根据EMD 分解得到的5个IMF 中分别计算RMS值Xrms、标准偏差σ、峰度因子K4、峰值因数Ip和波因子Sf这5个无量纲特征，形成30 维向量：F=

利用上述计算得到的高维特征向量，应用PCA算法将特征维数降维，通过对高维相关变量空间进行降维映射，将其转化为相互独立的低维变量空间，实现对复杂过程数据的特征抽取，建立相应过程的数学模型[6-8]。投影过程如下：

（1）对原始数据进行筛选整理及标准化处理的预处理，设[x(1),x(2),…,x(m)]为m维向量，归一化处理如下；

（2）利用预处理数据，计算协方差矩阵[8-10]：

（3）对Σ进行特征分解，求得m个特征值λ1≥λ2≥Λ≥λm≥0 及特征值对应的单位特征向量矩阵P；

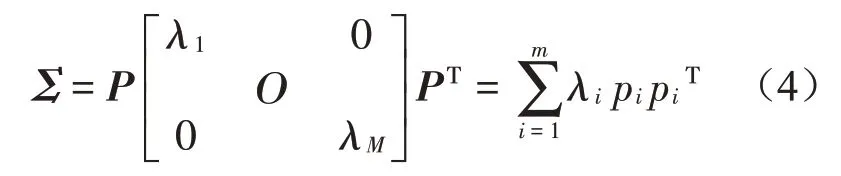
（4）按降序对特征值进行排序，确定最优的主成分数l，选取载荷矩阵；

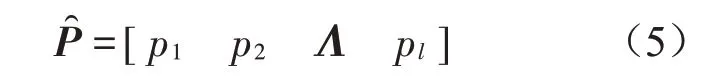
1.3 故障检测

利用正常运行条件下的测量数据建立PCA模型之后，将测量数据空间划分为主成分子空间和残差子空间[9-10]。在正常运行条件下，测量数据将主要投影到主成分子空间，投影到残差子空间的部分很小。反之，如果测量数据有异常或故障，测量数据投影到残差子空间的部分将明显增加。本文用过比较平方预测误差（SPE）和置信限（δ2）来检测螺栓松动故障；如果SPE≤δ2，则认为螺栓正常；如果SPE＞δ2，则认为螺栓发生松动，存在故障或异常。测量矩阵X可分分解为两部分。

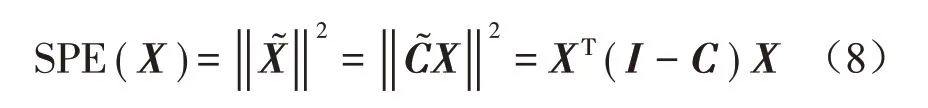
SPE可根据其定义式从测量数据矩阵中计算得到。SPE的置信限δ2可用式(9)计算得到。

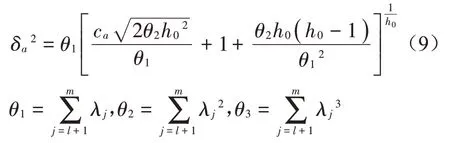
h0=式中：ca为正态分布的置信限；λ为协方差矩阵的特征值。

2 螺栓松动故障诊断试验研究

本研究在智能供水系统试验台架上进行，该系统可以模拟多种故障类型，如图1所示。可实现振动速度、振动加速度、管路压力、温度、转速等信号的采集和监控，并对系统常见故障进行识别和诊断。为揭示螺栓松动程度随电机振动响应特性变化的规律，在实验室现有的条件下，通过8个内六角螺栓将电机与底板连接，在泵和电机端基座分别安装振动加速度传感器，用于采集基座的振动信号。

图1 电机基础螺栓松动试验台架

采用PCA 方法对智能水系统台架螺栓松动故障进行检测。在系统正常运行条件下，测得一组数据，建立PCA模型。在其他工况不变情况下，分别载入螺栓松动一圈和松螺松动半圈的故障案例，并通过建立的PCA模型分别检测出螺栓松动的故障。在每次测试中，只有一个螺栓出现松动故障。

通过电涡流传感器获得轴转速，同时利用振动加速度传感器采集机脚的加速度信号。利用试验设备提供一个正常、螺栓松动0.5圈和1圈的松动故障样本，将采集数据进行数据过滤后输入已建PCA模型。设置65 536 Hz的采样频率，在每个工况下采样120 s，并将其分割成1 920个样本，样本经EMD分解后数据见图2，其中每个样本数据由4 096个点组成，1 000个样本用于训练，920个样本用于测试。

3 基于PCA的螺栓松动故障检测方法

3.1 建立PCA模型

利用上述算法对采集的信息进行处理，可得到1 000个样本的30维特征向量。

图2 螺栓松动信号的EMD分解

首先，计算样本数据的协方差矩阵Σ，然后，对Σ进行特征分解，求得其单位特征值和特征向量矩阵P，按降序排序的特征值如表1所示。

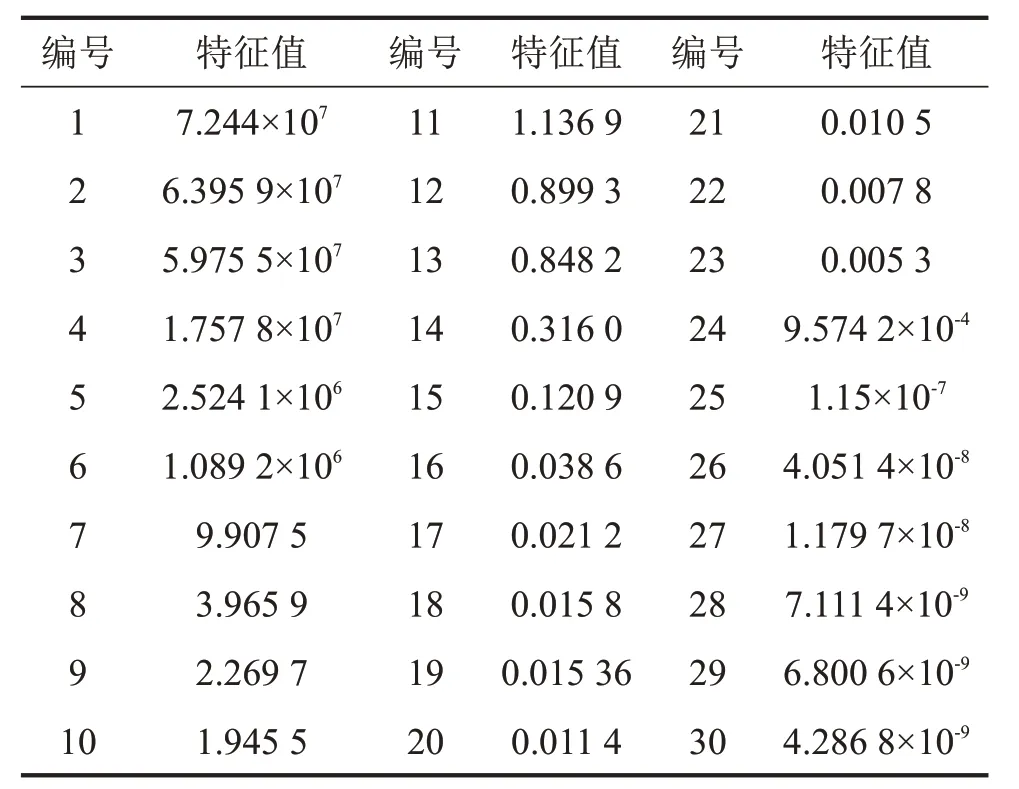
表1 训练样本的特征值

根据主成分分析法的原理，将N维数据降到K维数据主要是依据K维数据的坐标轴包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，从表1中可以看出，前6个特征值远大于其他特征值，于是，将前6个特征值对应的特征向量组成特征向量矩阵P^，从而得到主成分子空间PCS 和残差子空间RS的投影矩阵。由此，系统的主成分分析模型就被建立起来。

利用已建的PCA模型可计算SPE（测量向量X在RS内投影的平方）统计量的δ2置信限。经计算得到此时95%的δ2置信限为33.29。正常运行数据被用来检验已建立的PCA模型的正确性，其结果如图3所示。所测量数据的SPE值都在δ2控制限以下，从图中可以看出，所有数据均未超出置信限，表明系统运行正常，没有故障发生，同时也验证PCA模型建立的正确性。此时，当新的监测数据被采集到时，就可以对其进行检测。

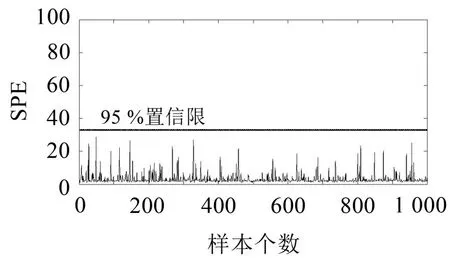
图3 正常数据的检测情况

3.2 故障测试验证

利用试验设备提供一个2只螺栓完全松动的故障样本，将采集数据进行数据过滤后输入已建立的PCA模型，故障开始的时间对应第501个样本，检测结果如图4所示。

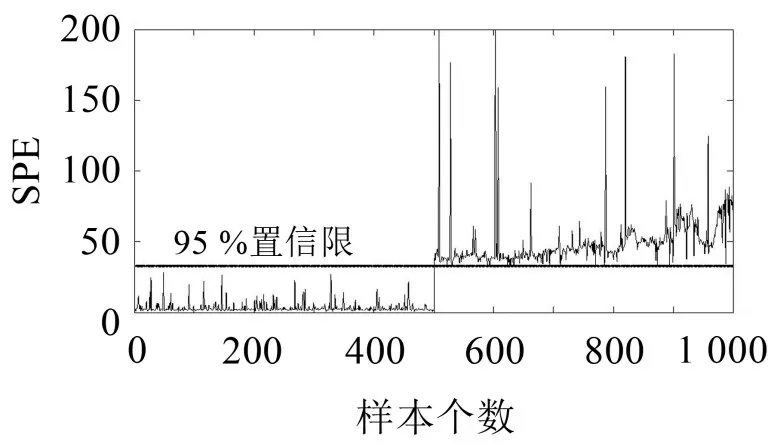
图4 螺旋松动故障检测数据值对比图

结果表明，在正常运行状态下，所有测量数据的SPE值都在95%置信限以下，可以判断系统运行正常，在输入4只螺栓完全松动的故障样本之后，可以看到从第501个样本开始，SPE值明显增加且超过了95%置信限，该对比结果验证了所建立的PCA模型检测故障的能力。

4 螺栓松动故障诊断测试

4.1 螺栓松动半圈工况测试

人为造成螺栓松动半圈故障，故障开始时间对应第一个样本。利用已建立PCA模型对故障数据进行检测，检测结果见图5。结果表明，当引入松动半圈故障后，样本的SPE值明显增加，部分样本的SPE值超过了置信限δ2，可以识别出系统螺栓出现松动，但也可以看到较多样本的SPE值处于置信限δ2的范围之内，说明八个螺栓中一个松动半圈造成的故障偏小，绝大多数采集的样本仍处于正常范围之内。

4.2 螺栓松动一圈工况测试

为进一步验证PCA模型对故障的检测能力，人为造成螺栓松动一圈故障并进行监测，检测结果见图6。

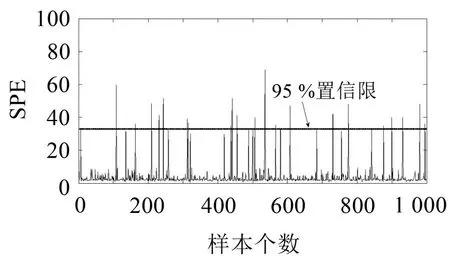
图5 单个螺栓松动0.5圈故障SPE值

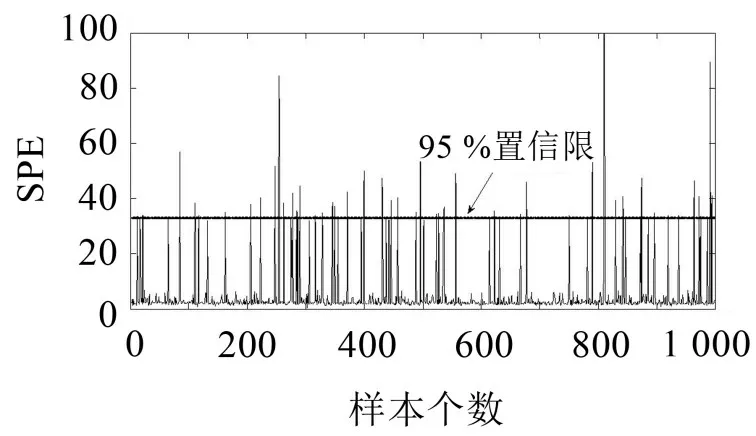
图6 单个螺栓松动1圈故障SPE值

可以看到，当引入松动一圈故障后，所有样本的SPE值都明显增加，有较多样本的SPE值超过了置信限δ2，可以明确识别出系统螺栓出现松动，说明单个螺栓中松动一圈后造成的故障样本相较于松动半圈的数据明显提升，置信限δ2的取值符合实际试验的客观规律。

4.3 频谱图对比

对正常状态下的数据样本和螺栓松动1圈的数据样本进行频域分析，图7显示了两种工况下振动幅值的频域分布状况。

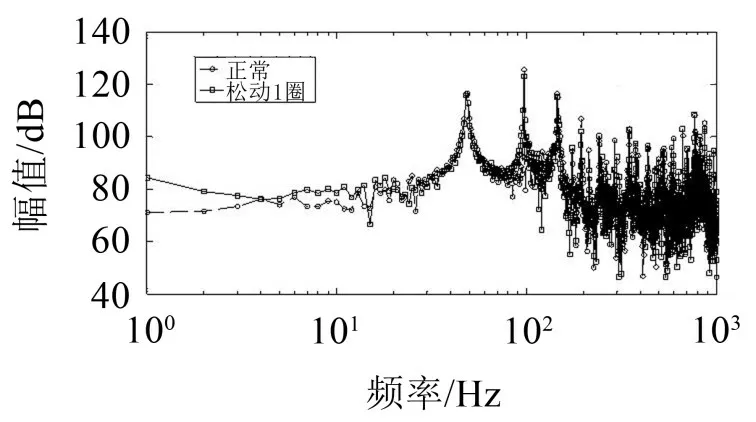
图7 频谱分析图

从频谱图中可以看到，两组数据在所测频段混杂在一起，很难明显判别出螺栓松动与正常情况，仅从频谱特性很难对螺栓松动故障进行判断，因此，相较于频域分析的方法，文中提出的基于PCA的故障检测方法可以更有效判别螺栓松动故障特征。

5 结语

本文提出了基于一种主成分分析法（PCA）的螺栓松动故障诊断方法，并进行了试验验证。首先对原始数据和由IMF组成原始特征向量的域特征进行了计算，在PCA模型建立后，计算了试验数据样本的SPE值作为故障检测的指标。在电机螺栓振动系统中对螺栓松动偏差故障进行了检测，试验结果显示基于PCA的故障检测方法可以较为明显检测出螺栓松动0.5 圈和1 圈的偏差故障，结果表明，基于PCA的螺栓松动故障检测方法是合理可行的。