复Finsler流形上的Laplace算子及其应用

邱春晖

(厦门大学数学科学学院，福建 厦门 361005)

1941年Hodge[1]提出了著名的Hodge定理:在任一紧致可定向的Riemann流形M上，所有次数等于p的调和形式组成的空间是一个有限维的向量空间，它的维数就是流形M的第p个Betti数.Hodge定理说明了M上的解析不变量等于拓扑不变量，不仅大大增强了对代数流形的理解，也将分析和拓扑意想不到地紧密联系起来，对这两大数学分支的迅速发展起着重要的作用.因此，著名数学家Witehead曾说过Hodge定理是20世纪最重要的定理之一.整体Riemann几何的基础工作之一是调和形式的Hodge理论.

熟知，Laplace算子在微分几何的调和积分理论和Bochner技巧中起着重要的作用.有关Kähler几何的调和积分理论，可参考文献[7-8].20多年来，在著名数学家陈省身先生的倡导下，实和复的整体Finsler几何取得了很大的进展[9-10].陈省身[11]指出：“Finsler几何可能在复域上是最有用的，因为每一个有边或无边的复流形都存在Carathéodory和Kobayashi拟度量.在适当(虽然有点严格)的条件下，它们都是C2度量，最重要的，它们自然都是Finsler度量.复Finsler几何是极其美丽的.”陈省身[12]还指出:“将调和积分理论推广到Finsler情形，将是微分几何研究的一块新园地，预计前景无限.”

研究Finsler流形上的调和积分理论和Bochner技巧的关键是定义一个适当的Laplace算子.目前，实和复Finsler流形上的Laplace算子取得了一些成果[13-23],但复Finsler流形上Laplace算子还没有统一的定义，主要有3种定义方法:第1种是在底流形M上定义Laplace算子[16,20-22];第2种是在全纯切丛T1,0M或射影丛PT1,0M或球丛SM上定义Laplace算子[17,19,23];第3种是定义均值Laplace算子[18].

1 复Finsler流形M上的Laplace算子

定义1[9]—个连续函数F:T1,0M→R+称为复流形M上的复Finsler度量，如果它满足下列性质：

(iii)F(ζv)=|ζ|F(v),对所有的v∈T1,0M和ζ∈C.

记为〈·,·〉,与此相关的Kähler形式

其中水平部分和垂直部分分别记为

定义2对于任意的ξ,η∈T1,0M,在T1,0M上定义内积

(1)

将内积延拓到∧p，qM.设φ，ψ∈∧p，qM,在局部坐标下

(2)

dVɡ

其中

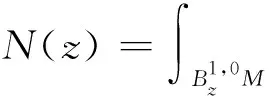
显然，N(z)是一个实值函数.类似于文献[20]中命題3.1,有

定义

其中

定义3设(M,F)是复n维强拟凸紧复Finsler流形.两个形式φ,ψ∈∧p,qM的整体内积定义为

(3)

显然定义3是整体定义的.并且

(4)

容易验证(，)满足下列性质：

(i)(φ,φ)≥0,并且(φ,φ)=0当且仅当φ=0;

(ii)(aφ+bφ,ψ)=a(φ,ψ)+b(φ,ψ),对任意的φ,φ,ψ∈∧p,qM和a,b∈C;

注2如果F是一个Hermite度量，则

N(z)=vol(B1,0M)ɡ(z),

∀ψ∈εp,q+1(M).

(5)

由于

我们有

(6)

其中

定义5Laplace算子定义为

(7)

显然Δ是一个自共轭算子，即对任意的φ,ψ∈Lp,q(M),有

(Δφ,ψ)=(φ,Δψ).

(8)

如果f∈C∞(M)，则由式(7)，有[20]

对于一般情形，有

注3如果F是Hermite度量，则

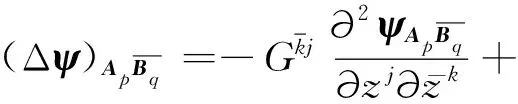
定理3[22]Laplace算子Δ是椭圆算子.

定义6对∀ψ∈Lp，q(M),如果Δψ=0,则称ψ为调和的.

我们有如下的关于Laplace算子Δ的Hodge分解定理.

定理5[22]设(M,F)是复n维强拟凸紧复Finsler流形，则

其中Dolbeault上同调群Hp,q(M)=Zp,q(M)/Bp,q(M),

2 T1,0M{0}上的Hodge-Laplace算子

相应的，对φ∈p，q;r，s，有

∂φ∈p+1,q;r,s⨁p,q;r+1,s⨁p+1,q+1;r,s-1⨁

在局部标架下，

引理1[26]设φ∈p，q;r,s，则

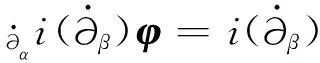
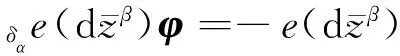
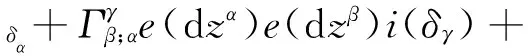
根据微分形式的类型，定义下列算子[16,26]

D=e(δvα)▽

(9)

(10)

定义7[16,26]设(M,F)是强拟凸紧复Finsler流形.两个形式φ,ψ∈p，q;r，s的整体内积定义为

(11)

容易验证(·,·)满足下列性质：

(i)(φ,φ)≥0,并且(φ,φ)=0当且仅当φ=0;

(ii)(aφ+bφ，ψ)=a(φ,ψ)+b(φ,ψ)对任意的φ，φ,ψ∈p，q;r，s和a,b∈C;

类似于Hermite几何[27],可定义Hodge星算子[16,26]

使得对任意的φ∈p，q;r，s

定理6[16,26]设(M,F)是复n维强拟凸紧复Finsler流形.则Hodge星算子*:满足：

(iii)**ψ=(-1)p+q+r+sψ.

由共扼性,有

我们可定义d的伴随算子d*=-*d*,则

(12)

容易看到

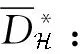
令φ∈p-1，q;r，s，ψ∈p，q;r，s，由微分形式的类型，有

类似地，

(D

由共扼性可得

定理7[26]设(M,F)是复n维强拟凸紧复Finsler流形，则

定理8[26]设(M,F)是复n维强拟凸紧复Finsler流形，则对任意的φ∈p，q;r，s,有

定义9定义下列微分算子：

注4文献[16]中定理5.7也给出了强拟凸紧复Finsler流形关于复Rund联络D同样的公式.实际上Δf=d*df的公式不依赖于复Rund联络或Chern-Finsler联络的选择.

显然，根据保持类型，Hodge-Laplace算子Δ=d*d+dd*可表示为

则对任意的φ,ψ∈p,q;r,s,有

因此，形式φ∈p，q;r，s为Δ-调和的当且仅当

定理10[26]设(M,F)是复n维强拟凸紧复Finsler流形，利用Chern-Finsler联络，可得

定理11(消灭定理)[26]设(M,F)是复n维强拟凸紧复Finsler流形.对任意的φ∈p,0；r,s,如果

则不存在非零的φ∈p，0；r，0使得

3 射影切丛PT1,0M上水平复Laplace算子

记

ω

则PT1,0M整体不变体积形式为

其中

记

Ap=(α1,…,αp),α1<α2<…<αp,1≤αi≤n,

An-p=(αp+1,…,αn),αp+1<…<αn,1≤αi≤n,

其中(α1,…,αp,αp+1,…,αn)是(1,2,…,n)的一个置换.类似地，记Bq=(β1,…,βq),Bn-q=(βq+1,…,βn),Cp=(c1,…,cp),Cn-p=(cp+1,…,cn),Dq=(d1,…,dq),Dn-q=(dq+1,…,dn),在这些记号下，p,q的元素在局部坐标下的表达式为

(13)

其中

(14)

设φ∈则算子p,q→p，q+1定义为

其中

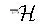
引理2[21]设(M,F)是复n维强拟凸紧复Finsler流形，则对任意的φ∈p，q,有

低阶项.

定理12[21]设(M,F)是复n维强拟凸紧复Finsler流形，则对任意的φ∈p，q,有

εp，q(M)作为p，q的子空间，其内积(·,·)由p，q所诱导，即对任意的φ,ψ∈εp，q(M),有

(φ,ψ)=(φ,ψ)PT1,0M.

(15)

记

则

设φ,ψ∈εp,q(M),定义[21,27]

(16)

则

(17)

利用PT1,0M上光滑水平(p,q)形式的内积(·,·)PT1,0M，取p,q的2闭包，记为Lp,q(PT1,0M).和的弱延拓仍然保持Lp,q(PT1,0M).因此,在Lp,q(PT1,0M)上是整体定义的，称为水平复Laplace算子.

引理4[28]设(M,F)是强拟凸紧复Finsler流形，则对任意的φ∈p,q，有

定理13[28]设(M,F)是复n维强拟凸紧复Finsler流形，则对任意的φ∈Lp,q(M),有

定理14[28]设(M,F)是复n维强拟凸紧复Finsler流形，则

注10如果复Finsler度量F是Kähler Finsler度量，则定理14退化成紧Kähler Finsler流形上水平复Laplace算子的自然投影的Hodge分解定理.

定义14如果□φ=0,则φ∈Lp,q(M)称为M上的调和(p,q)形式.

定理15[29]Hodge-Laplace算子□是自共扼的椭圆算子.

利用自共扼椭圆算子的分解定理，有如下的关于Hodge-Laplace算子□的Hodge分解定理.

定理16[29]设(M,F)是复n维强拟凸紧复Finsler流形，则

(i)M上所有调和(p,q)形式组成的空间Hp,q(M)={φ∈Lp,q(M)|□φ=0}⊆εp,q(M),并且，dimHp，q(M)<∞.

定理16说明了调和(p,q)形式空间Hp，q(M)与Dolbeault上同调群同构.

注12如果复Finsler度量F是Kähler度量，则算子□就是Kähler流形上通常的Hodge Laplace算子.因此，定理16退化成紧Kähler流形上的Hodge分解定理.

复Finsler流形上Laplace算子及其应用的研究刚刚开始，期待有更多的研究成果.