2020年高考数学试题亮点扫描

仓万林 李 红 (江苏省江阴市要塞中学 214432)

钱 鹏 (江苏省南通市天星湖中学 226010)

2020年高考数学试题是教学改革的风向标．《中国学生发展核心素养》提出了核心素养的总体框架和基本内涵，高考评价体系确立了高考中学科素养的考查目标，这标志着中国高考正在实现从能力立意到素养导向的历史性转变．[1]

纵观2020年的8份高考数学试题(全国卷3份，自主命题和新高考(山东卷)5份)，许多试题给人感觉耳目一新，试题设计重视学科本质，突出了数学阅读、数学文化、数学应用、数学探究的引领作用，加强了对核心素养的考查，有转型期高考试题风向标的价值，必将对今后的教学行为产生潜移默化的影响．

1 彰显数学文化

经过多年的尝试，数学文化进入高考试题已经成为一种新常态．尤其是湖北卷从2008年到2015年八年一贯的对数学文化试题的探索，如2015年高考中的“鳖臑”问题，引起了社会对数学文化的广泛关注，推动了数学文化的大众传播，成为一种社会文化现象．据笔者不完全统计，2020年高考中的数学文化试题概况如表1．

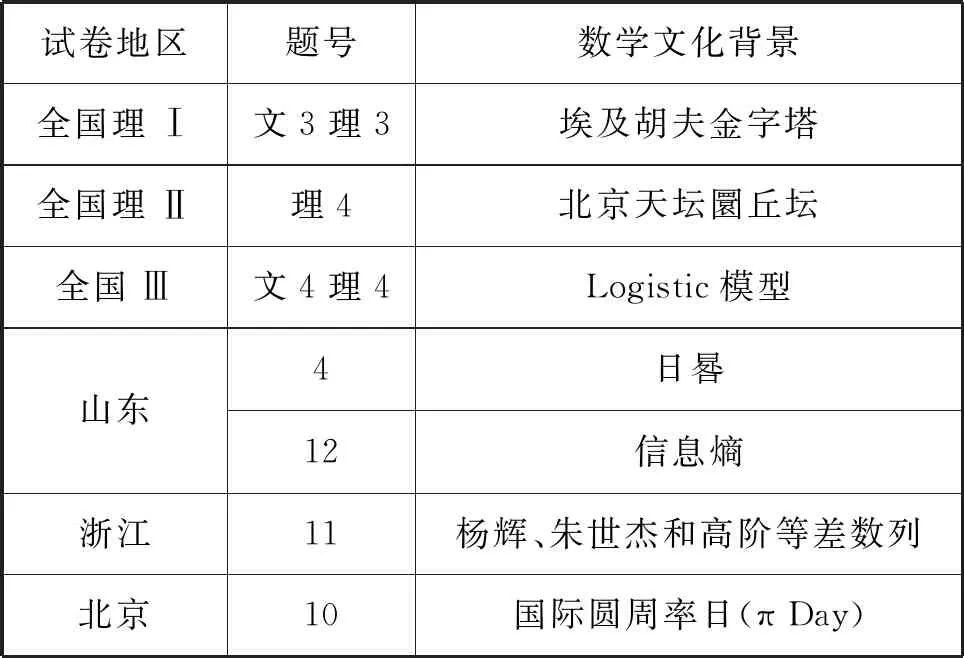
表1

例1(2020年北京)2020年3月14日是全球首个国际圆周率日(π Day)．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似，数学家阿尔·卡西的方法是：当正整数n充分大时，计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是( )．

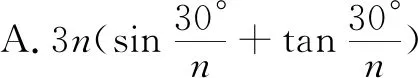
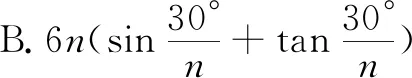
图1

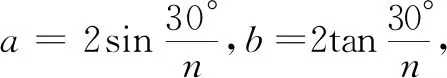
点评本题以圆的几何性质为载体考查数学文化，使学生在应用数学知识解决问题的过程中开阔视野，感悟数学之美，培养数学学科素养．

试题背景赏析圆周率π就是一个传奇．

这些数学家建议“τ宣言”，还在6月28日庆祝“真正的”圆周率日(图2)．

图2

如果在今后的高考试题中遇到这样的问题，你还会奇怪吗？

以数学文化为载体的高考试题，成为新课程背景下高考改革的一道靓丽风景，试题讲究素材背景的文化性和数学美的呈现，使考生在丰富多彩的试题背景中实现知识和信息的迁移，体验数学之美和数学文化．数学的文化性、应用性与理论性有机结合，相互渗透，真正考查考生的学习潜能和数学素养．试题促使数学文化进入高中数学课堂教学实践，引领教师去挖掘和探究课程中的数学文化元素，把数学文化教育潜移默化地渗透到课堂教学，达到数学学科立德树人的目的．

2 注重开放性题型

2020年高考数学试题在题型上进行了大胆改革和创新，开放性题型逐渐进入到我们的视野，成为一大亮点．

开放性命题颠覆了我们对于传统考查方式的认知，给学生提供了更多的自行搜索解答路径、检索知识储备、思维发散、综合解答问题和探究创新的可能，能够赋予学生更多自由发挥的空间．问题没有固定的模式，推动学生必须经过主动思考，综合运用观察、分析、归纳、推理等方法，在多角度、多方位思考问题的过程中发展其创新意识和实践能力．同时，问题的思维性和开放性使得开放命题符合了发展核心素养的要求．[2]

和以往的谨慎尝试相比，2017—2020年的北京卷，均在开放性命题方面作出了可贵的探索．

题1(2017年北京文/理)能够说明“设a,b,c是任意实数，若a>b>c，则a+b>c”是假命题的一组整数a,b,c的值依次为．

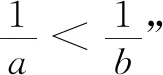
题3(2018年北京理)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立，则f(x)在[0,2]上是增函数”为假命题的一个函数是．

题4(2019年北京理12/文13)已知l,m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题．

题5(2020年北京14)若函数f(x)=sin(x+φ)+cosx的最大值为2，则常数φ的一个取值为．

结构不良问题是开放性题型的重要形式之一，具有很好的开放性，可能缺少解决问题的必要条件或者某个条件存在变数，其结论也是多样化的，甚至在某些特定条件下问题是无解的，问题的解决过程更是千差万别．高考中的结构不良试题，能够有效地考查学生建构数学问题的能力、分析问题和解决问题的能力，对数学理解能力、数学探究能力的考查是积极和深刻的．

注：如果选择多个条件分别解答，按第一个解答计分．

点评问题以解三角形为背景，给定若干条件(在这些条件下并不能确定三角形)，要求学生在另外给出的几个条件中自主选择，若问题中的三角形存在，求解三角形；若问题中的三角形不存在，说明理由．选择本身是试题要考查的内容之一，不同的选择可能导致不同的结论，难度与作答时间也会有所区别．

数学开放题的核心是培养学生的创造意识和创造能力，激发学生独立思考和创新的意识，是新的教育理念和课程理念的具体体现．高考试题中开放题的出现，有助于引导我们走出课堂教学中过度训练的传统误区，切实将教和学的重心转移到数学方法和思维训练上．

3 突出数学应用

数学应用问题是高中数学教学和考查的重要内容之一．自20世纪80年代第三次数学课程改革运动以来，数学应用引起世界各国关注，多个国家纷纷进行数学课程改革．培养学生应用数学解决问题的能力、建立简单数学模型并利用模型解决实际问题的能力已成为现代数学课程目标的主要内容之一．数学学科核心素养中的数学建模、数据分析等直接和数学应用问题密切相关．在数学教学活动中，加强建模能力的培养，“有利于学生养成用数学的眼光观察现实世界的习惯，有利于学生发展用数学的思维分析实际问题的能力，有利于学生形成用数学的语言表达实际问题的能力”[3]．

A．60 B．63 C．66 D．69

点评问题以新冠肺炎疫情传播的动态研究为背景，用数学模型揭示疫情遏制阶段的规律，选择适合学生知识水平的模型作为试题命制的基础，考查使用数学模型解决实际问题的能力．

(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数)；

(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01)；

(3)根据现有统计资料，各地块间植物覆盖面积差异很大．为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由．

(3)更合理的抽样方法是分层抽样，根据植物覆盖面积的大小对地块分层，再对200个地块进行分层抽样．

理由如下：由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关．由于各地块间植物覆盖面积差异很大，使得各地块间这种野生动物数量差异也很大.采用分层抽样的方法较好地保持了样本结构与总体结构的一致性，提高了样本的代表性，从而可以获得该地区这种野生动物数量更准确的估计．

点评试题以沙漠治理为背景，考查学生分析问题和解决问题的能力、数据处理的能力以及创新应用的能力．问题设计体现了新课程标准的基本理念，融数学建模和数学探究于其中，在不同版本的教材中，我们都可以发现问题的原型，源于课本又不拘泥于课本．

可以预见，应用问题的考查在今后会越来越被重视.该试题的出现也提醒我们一线教师，应用问题考查的方式可以多样化．另外，试题在建立模型之后的方案选择上，也体现了适当的开放性．试题也折射出数学阅读和表达的重要性．阅读理解是基于思维的认识活动，直接影响着人们发现问题和解决问题的能力，它既是获取知识的一种能力，也是影响思维和认识的一种重要能力．问题设计对表达能力有明显的要求，立足于全面考核学科素养，而这恰恰是我们在平常教学中所容易忽视的．可以预见，数学阅读和数学写作等隐性课程要素将在今后的课堂教学实践中得到越来越多的体现．

高考是大事，关注2020年高考题中的亮点和变化，无疑会给我们的教和学带来更多的启迪．