用于堆芯装载方案优化的遗传算法算子设计
郭 建,秦玉龙,王丽华,杨庆湘
(上海核工程研究设计院有限公司,上海200233)
广义的堆芯装载方案优化问题是多变量、多目标、多约束的复杂问题,直接使用数学优化中的方法求解,难度很大。在实际换料设计中,最常见的堆芯装载方案优化问题是一个单循环且固定燃料富集度、可燃毒物配置及换料燃料组件数目的多目标组合优化问题,即单循环堆芯装载方案优化问题。多数堆芯装载方案优化研究主要关注单循环、单目标堆芯装载方案优化问题。遗传算法作为一种通用的优化策略已广泛应用于多个工程优化领域[1],正逐渐成为解决堆芯装载方案优化问题的重要工具。如Tanker等应用遗传算法研究堆芯装载方案优化问题,取得了一定的优化效果[2];咸春宇等研究了遗传算法在堆芯装载方案优化问题中的编解码方法[3];王涛等通过将遗传算法与其他算法混合使用,改善了优化效果[4]。虽然这些研究将遗传算法用于堆芯装载方案优化问题,实现了编码、译码和遗传操作,但研究中大多使用通用的遗传算子,且对相关遗传算子的优化结果未进行对比分析。本文从组合优化问题的角度出发,首次对堆芯装载方案优化中各种组合优化算子的优化效果进行了对比分析,设计了一种适用于整数编码的交叉算子和变异算子,并使用分段整数编码,确保编码具有完备性、合法性和拉马克性质。
1 遗传算法
遗传算法是一种强有力且应用广泛的随机搜索和优化方法,是当前影响力最大的进化算法之一。20世纪60年代,Holland首先提出遗传算法[5]。该方法模拟了生物在自然界的演化过程,原理源于达尔文的“自然选择”法则,即在演化过程中,那些存活的个体既不是最强大的个体,也不是最聪明的个体,而是最能适应变化的个体。遗传算法作为一种通用的随机搜索策略,不需要提供变量之间的关系式,非常适于解决堆芯装载方案优化这种多变量耦合且解空间非常大的优化问题。
1.1 带精英策略的遗传算法
本文使用一种包含精英策略的遗传算法。Rudolph等使用齐次有限马尔科夫链方法,证明了经典遗传算法无论如何选择初始种群、交叉算子和目标函数,均无法保证算法收敛于全局最优解[6];但精英策略通过保留种群中的最优个体,可使遗传算法收敛于全局最优解。在单目标遗传算法中,精英策略一般指在种群中保留目前搜索到的已知最优解[7],无论精英策略的执行是在选择前还是在选择后,均可使遗传算法具备全局收敛特性。
1.2 编码和新解的产生方式
在实际的单循环换料设计中,新燃料组件的富集度、位置和可燃毒物的装载方式通常已基本确定,只需对“旧料”进行重新排列。大型先进压水堆的堆芯一般采用低泄漏换料方案[8],可以直接将外围燃料组件布置为“旧料”中反应性最低的燃料组件,降低需要排列的燃料组件数量。实际的单循环堆芯装载方案设计中,“旧料”的布置可以近似为一个组合优化问题。此外,燃料组件内部有一定的燃耗梯度倾斜,通过旋转燃料组件,改变其与堆芯中心位置的相对朝向,可以小幅度地展平功率分布,延长循环长度。
本文使用整数编码的方式处理燃料组件的排列组合和旋转。整数编码也称为字符编码,是离散优化问题最适合的编码方式,可以保证编码所表示的解具有合法性、完备性和拉马克性质[9]。合法性是指编码中基因的所有可能排列均对应着一个可行解,不存在编码无法解析为可行解的情况。整数编码与组合优化算子同时使用才能保证遗传操作中解的合法性。完备性是指任意解均对应着一组编码,可以保证解空间中的任意解在遗传搜索过程中都是可搜索到的。拉马克性质是指染色体编码中某个基因的等位基因含义不依赖其他基因。编码具有拉马克性质可以保证遗传操作的有效性。使用实数编码处理组合优化问题时,一般需要对编码进行修补,防止产生非法解。当使用基因的排列顺序对编码进行修补时,无法保证编码具备拉马克性质。
本文使用分段整数编码表示带燃料组件旋转的堆芯装载方案优化算法中的一个可行方案。堆芯装载方案设计需要满足燃料组件1/4对称布置要求,因此,只需要对1/4堆芯进行编码。堆芯装载区域的位置编号及燃料组件编号,如图1所示。中心燃料组件可以参与优化,但多数情况下,中心燃料组件可由经验直接指定。确定位置编码和燃料组件编号后,可以获得一个可行解编码。图2为分段染色体编码。其中,编码可分为2段,前半段(0~22)表示燃料组件位置,染色体位置的序号和堆芯装载区域位置的序号相对应,染色体基因表示可用燃料组件的序号,在旅行商问题中这种表示方式称为路径表示;后半段表示燃料组件的旋转角度,分别用0,1,2,3表示绕中心旋转0°, 90°, 180°, 270°。分段编码后,1条染色体既可确定燃料组件的位置,也可确定燃料组件的旋转角度。

(a)Location id
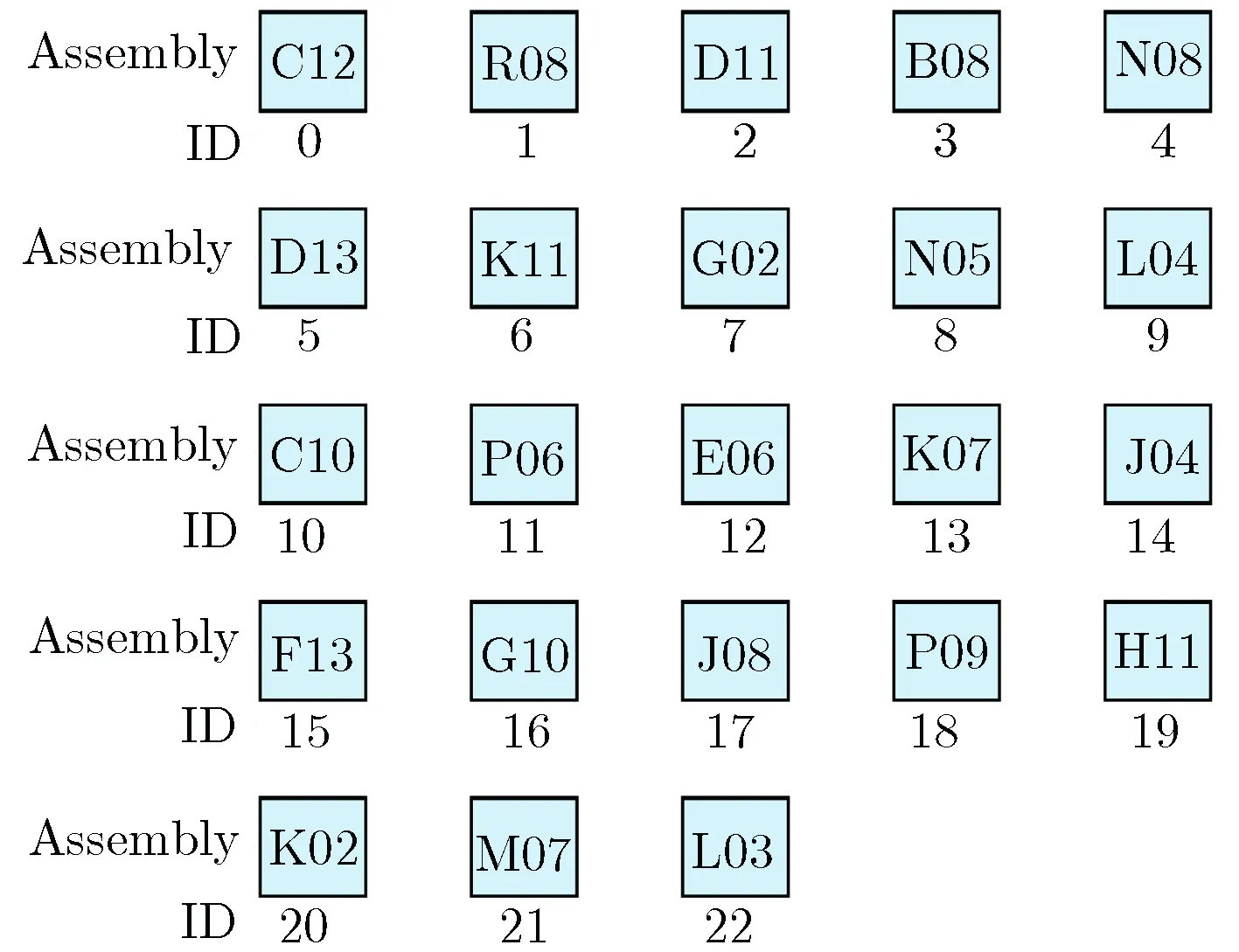
(b)Fuel assembly id图1堆芯装载区域的位置编号及燃料组件编号Fig.1 Location id and fuel assembly id for optimization of core load pattern

图2 分段染色体编码Fig.2 Segmented coding of chromosome
分段编码不仅能表示燃料组件的位置、旋转角度等不同类型信息,保证解的完备性,而且能应用不同的遗传算子。遗传算法通过交叉、变异等操作产生新的可行解。燃料组件位置的编码是一串整数的排列,进行交叉、变异等遗传操作后,解的合法性不应被破坏。因此,本文为保证解的合法性,对于分段整数编码中的不同片段使用不同的遗传算子进行交叉、变异等操作,编码的前半段是组合优化问题,采用组合优化中使用的算子,编码的后半段使用遗传算法中常用的遗传算子。
1.3 并行算法
遗传算法的计算速度较慢,计算量主要集中在对大量可行解的评价,通常要对数以万计甚至十万计的可行解进行评价后才能得到优化解。但遗传算法具有良好的并行特性,同代个体的适应值计算不存在相互依赖问题,且适应值计算为遗传算法计算量的主要部分。本文基于MPI并行实现了并行遗传算法,可以充分利用多个服务器的计算资源,大幅度提高算法的执行效率。除适应值计算流程外,并行遗传算法的计算流程与原来的遗传算法计算流程一致。并行遗传算法将种群按照进程数等分(种群数量无法被进程数整除时近似等分),每个进程负责所分配的个体适应值计算,所有进程均完成计算后,汇总适应值计算结果,然后按照正常的步骤进行遗传算法中的选择、交叉和变异操作。带精英策略的并行遗传算法计算流程,如图3所示。
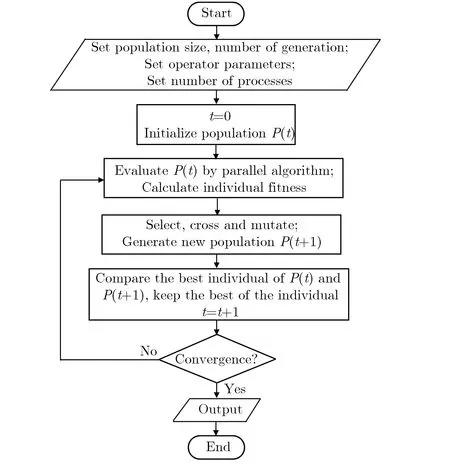
(a)Calculation flow chart

(b)Parallel algorithm图3带精英策略的并行遗传算法计算流程Fig.3 Flow chart of parallel genetic algorithm with elitism
2 组合优化算子
单循环堆芯装载方案优化是一个近似的组合优化问题。本文对堆芯装载方案设计过程进行深入分析,参考实际的优化过程,提出了一种基于随机子路径的交叉算子和一种基于随机子路径的变异算子应用于旅行商问题及单循环堆芯装载方案优化问题,并与其他多种组合优化算子的优化效果进行了对比分析。
2.1 随机子路径算子
在实际的单循环装载方案设计中,通常将几个位置的燃料组件调换次序以获得更好的装载方案。用随机子路径算子模拟该过程时,随机子路径算子会随机选择一些燃料组件,这些燃料组件的排列构成子路径。然后,对这些燃料组件的次序进行某种操作产生新的可行解。本文在随机子路径算子中引入交换概率Pe,用于表示随机选取子路径过程中燃料组件被抽中的概率。
2.1.1随机子路径交叉算子
随机子路径交叉算子(discontinuous sub-tour exchange crossover, DSE)先按照交叉概率Pc选择成对个体作为父代,再按照交换概率Pe随机选取一些燃料组件,保持燃料组件在父代中的顺序不变,交换对应位置的子路径。随机子路径交叉算子,如图4所示。其中,箭头表示随机选择的燃料组件及其位置,父代1个体的随机子路径为(2, 5, 6, 9),父代2个体的随机子路径为(5, 6, 9, 2),在交叉过程中子路径的顺序不变。在选择子路径过程中,燃料组件是随机选择的,在对应的父代个体中,子路径可能是连续的,也可能是不连续的。
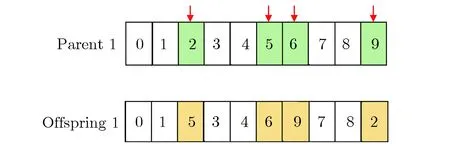

图4 随机子路径交叉算子Fig.4 Discontinuous sub-tour exchange crossover operator
2.1.2随机子路径变异算子
随机子路径变异算子(discontinuous scramble mutation, DSM)首先按照变异概率Pm选择一个个体作为父代;其次,按照概率Pe选择一些燃料组件生成子路径;最后,将子路径中的燃料组件打乱,并按照打乱后的顺序放回原来的位置。随机子路径变异算子,如图5所示。若随机选择的子路径为(3, 5, 7, 8),则打乱后子路径可以是(5, 7, 8, 3),将打乱后的子路径放回子路径原来的位置就得到一个新的可行解。本文的实际优化计算过程中,随机子路径变异算子的交换概率Pe与变异概率Pm取相同值。
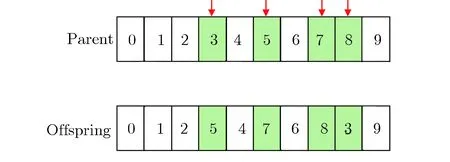
图5 随机子路径变异算子Fig.5 Discontinuous scramble mutation operator
2.2 组合优化算子
本文除提出了2种遗传算子外,还研究了经典组合优化问题中旅行商问题常用的多种基于路径表示的遗传算子,包括11种交叉算子和6种变异算子。这些遗传算子是专门针对组合优化问题设计的,在遗传操作中可保证不产生非法解。
2.2.1组合优化交叉算子
组合优化中常用的交叉算子,如表1所列。每个交叉算子的具体操作方式可参见相应的参考文献。这些交叉算子中, PMX和EX采用交叉和修补的方式产生新解;PMX使用子串的映射修补非法解;EX是由经典的2点交叉算子改进得到的,为了避免非法解的产生,使用基因的排列顺序对解进行修补;其余的交叉算子均不会产生非法的中间解。OX,OBX,PBX,SE,PMX,MPX这6种交叉算子也是基于子路径设计的,OX, SE, PMX, MPX这4种交叉算子按照2点交叉的方式选择子路径,OBX和PBX的子路径是离散的。交叉算子PBX, OBX, EX均引入了交换概率Pe用于调整交换基因的数量。 MPX和PMX的原理相似,在交叉操作中破坏的边界信息少,优化效果可能更好。VR是一个p-sexual交叉算子,即参与交叉操作的父代个体数量为p,p通常取2或4。ER是基于边界信息的交叉算子,比较适用于对称旅行商问题。AP通过按照顺序依次选择父代个体中的基因产生新的个体,选择过程中忽略已经选择过的基因。

表1 组合优化中常用的交叉算子Tab.1Commonly used crossover operatorin combination optimization
2.2.2组合优化变异算子
组合优化中常用的变异算子,如表2所列。表2中每个变异算子的具体操作方式可参见相关的参考文献。DM算子随机选择一个子路径,然后将子路径随机插入到染色体中。ISM算子的原理与DM算子相同,只是ISM的子路径仅包含一个基因。SIM和IVM随机选择一个连续子路径,SIM在原来的位置反转子路径中的基因,IVM将反转后的子路径随机插入到染色体中。SM选择一个连续子路径,将子路径随机打乱后放回原来的位置。EM算子和经典的互换变异操作相同,即交换染色体随机2个位置的基因。

表2 组合优化中常用的变异算子Tab.2Commonly used mutation operatorin combination optimization
3 计算结果
3.1 中国旅行商问题的优化结果
对中国旅行商问题(Chinese traveling salesman problem, CTSP),应用不同算子组合的数值实验,得到了相应的交叉概率、变异概率和交换概率的最佳选取方式,分析了不同算子的优化效果。中国旅行商问题中共有31个城市[15],表3列出了中国31个城市的坐标。从任意城市出发依次通过每一城市后返回出发城市的最短路径,即为该问题的最优解。中国旅行商问题的已知最短路径长度为15 381[16],路径示意图如图6所示。

表3 中国旅行商问题中的城市坐标Tab.3City coordinates for Chinese traveling salesman problem

图6 中国旅行商问题已知的最短路径Fig.6 The shortest known path to Chinesetraveling salesman problem
为了得到算子最佳交叉概率、变异概率和交换概率,使用不同的参数取值进行数值实验。数值实验中各参数的取值,如表4所列。在数值实验中,种群数统一取为500,演化代数统一取为200,使用竞标赛选择算子,统计得到各个交叉算子和变异算子组合在不同交叉概率、变异概率和交换概率下的最佳优化结果,如表5所列。分析表5中同一交叉算子与不同变异算子组合的平均路径长度可知,DSE,PBX, OBX的优化效果在12种交叉算子中的优化效果最好,这3种交叉算子与其他各种变异算子的组合均能获得良好的优化效果,且均获得了比目前已知最优解更短的路径,最短路径长度为15 378,路径示意图如图7所示。

表4 数值实验中交叉概率、变异概率和交换概率的取值Tab.4Probabilities for crossover, mutation and exchange in the numerical test

表5 中国旅行商问题数值实验得到的路径长度Tab.5Tour length for numerical test of Chinese traveling salesman problem

图7 用本文算子得到的中国旅行商问题最短路径Fig.7 The shortest path of Chinese traveling salesmanproblem based on the operator presented in this paper
本文提出的交叉算子DSE的平均值最低,优化效果最好。ER,OX,SE,MPX的优化效果次于DSE,PBX,OBX,优化路径平均长度均低于16 000,其余交叉算子的优化效果更次。
变异算子的引入是为了扩大遗传算法的搜索空间,避免陷入局部最优,但由于变异过程是随机的,引入变异算子后的可行解可能变好也可能变差。通过比较变异算子与不同交叉算子组合的优化结果可以看出,变异算子在遗传算法中的作用有限,当交叉算子的效果比较差时,变异算子并不能显著改善优化效果。综合比较变异算子与不同交叉算子组合的优化解平均值、最大值和最小值可以看出,SIM的效果最好,能明显改善PM交叉算子的优化效果。本文提出的变异算子DSM效果不突出,但在交叉算子优化效果较好时,DSM不会使可行解变差。
在分析最短路径长度的基础上,统计了各个交叉算子与DSM,SIM,IVM 3个变异算子组合获得最短路径时的相应参数,结果如表6所列。由表6可见,优化效果最好的3种交叉算子DSE,PBX,OBX对应的交换概率约为0.5,这表明交叉操作中2个父代个体交换一半的基因。对比变异概率为0.01和0.001时的结果可知,变异概率为0.01时的结果更好。统计得到路径长度随交叉概率的变化关系,如图8所示。由图8(a)可见,对于DSE,PBX,OBX,交叉概率变大时优化效果变好,交叉概率在0.7~0.9时优化结果较好。由图8(b)可见,对于AP和VR,交叉概率小于0.5时优化效果较好,交叉概率大于0.5时优化效果显著恶化;其他优化算子的优化效果随交叉概率的变化不发生明显改变。

表6 算子组合获得最优解时的参数取值Tab.6Parameters of operator combinations when obtain the best optimum solution
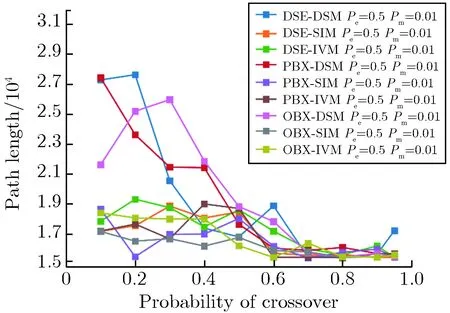
(a)Path length vs Pc for the combinations of 9 operators (b)Path length vs Pc for SIM with different crossover operators图8中国旅行商问题路径长度随交叉概率的变化Fig.8 Path length vs. crossover probability for Chinese traveling salesman problem
3.2 单循环堆芯装载方案优化问题
将本文提出的交叉算子DSE和变异算子DSM应用于单循环堆芯装载方案优化问题。为对比交叉算子的优化效果,根据中国旅行商问题的测试结果,在单循环堆芯装载方案优化问题中测试了不同交叉算子与SIM组合的优化效果。为测试变异算子DSM,对比了DSM与中国旅行商问题中优化效果较好的SIM和IVM变异算子。测试的算子组合只对编码的位置部分进行操作,编码的旋转部分使用同样的交叉和变异算子。旋转部分的交叉算子为均匀交叉算子[17],即在2个父代个体中随机选择一些基因位置并交换2个位置的基因。旋转部分的变异算子可从染色体中随机选择一个基因位置并改变该位置的基因。为方便比较,除AP和VR外,交叉算子的交叉概率统一取0.9,AP和VR的交叉概率均取0.3,交换概率统一取0.5,变异算子的变异概率取0.01,每代种群数为156,总演化代数为300,使用竞标赛算子。用实际工程中使用的核设计程序对可行解进行评价,为快速获得测试结果,以寿期初的硼质量分数为优化目标,硼质量分数越大,则可行解越好。在实际优化计算中也可根据需求选择其他的优化目标。本文测试的堆芯装载区域与图1类似,新燃料组件的位置固定不变,最外侧燃料组件为反应性最低的燃料组件,共包含13个燃料组件(1/4堆芯)的排列和旋转。
单目标堆芯装载方案优化问题中9种算子组合优化得到的初始临界硼质量分数,如表7所列。由表7可见,由于这9种算子组合是通过对中国旅行商问题测试得到的效果较好的算子组合,所以DSE,OBX,PBX 3种交叉算子的优化结果非常接近,优化后的临界硼质量分数均明显大于初始方案的临界硼质量分数1 764.4×10-6,3种交叉算子相互之间并没有明显的优势。变异算子中IVM和SIM的优化效果相当,略优于本文提出的变异算子DSM。
不同交叉算子和SIM变异算子组合优化得到的初始临界硼质量分数,如表8所列。

表7 单目标堆芯装载方案优化问题中9种算子组合优化得到的初始临界硼质量分数Tab.7Initial critical boron mass fraction for combinations of 9 operators of single-object core load pattern optimization problem

表8 单目标堆芯装载方案优化问题中不同交叉算子和SIM变异算子组合优化得到的初始临界硼质量分数Tab.8Initial critical boron mass fraction for SIM with different crossover operators of single-object core fuel load pattern optimization problem
由表8可见,在中国旅行商问题中优化效果好的交叉算子,如DSE,PBX,OBX,在单目标堆芯装载方案优化问题中的优化效果也较好,但在中国旅行商问题中最优的交叉算子(DSE,PBX,OBX)和次优的交叉算子(ER,OX,SE,MPX)之间优化效果的差异在堆芯装载方案优化问题中变小。在中国旅行商问题中优化效果较差的交叉算子,在堆芯装载方案优化问题中优化效果也较差。还有部分算子在这2个问题中的优化效果不一致,如ER和MPX在堆芯装载方案优化问题中的优化效果与在中国旅行商问题中的优化效果相比变差,CX算法的优化效果变好。
单目标堆芯装载方案优化问题中不同算子组合的收敛曲线,如图9所示。

(a)Convergence curve for combinations of 9 operators

(b)Convergence curve for SIM with different crossover operators图9单目标堆芯装载方案优化问题中不同算子组合的收敛曲线Fig.9 Convergence curve for different operator combinationsof single-object core load pattern optimization problem
由图9可见,除了AP交叉算子外,其他算子组合在100代附近均已收敛。由于使用了带精英策略的遗传算法,最优个体在种群中得到保留,所以收敛曲线是单调的。
4 结论
本文研究了单目标堆芯装载方案优化问题的遗传算子,提出了一种新的随机子路径交叉算子DSE和一种随机子路径变异算子DSM。测试结果表明,交叉算子DSE在单目标堆芯装载方案优化问题中的优化效果与PBX和OBX相当,DSE在旅行商问题中的优化效果优于其他算子。变异算子DSM在单目标堆芯装载方案优化问题中的优化效果与IVM和SIM算子相比略差。本文提出的基于分段整数编码进行遗传操作的新解产生策略,可以描述燃料组件的位置和旋转信息,避免了非法解的产生,具有良好的扩展性和通用性。后续将基于本文设计的优化算子开展多目标堆芯装载方案优化问题研究,给出多个优化目标下的结果。

