求解CMFD的改进流水线并行GMRES方法
郝 琛,韩立会,程有莹
(1.哈尔滨工程大学 核科学与技术学院,哈尔滨150001;2.国家核应急响应技术支持中心,北京100080)
基于特征线方法的全堆芯3维精细化物理计算方法是国际研究热点之一。目前,全堆芯精细化中子输运计算中多应用2维或1维聚合算法,并应用粗网有限差分方法(CMFD)加速3维输运计算[1]。在求解CMFD大型非对称线性稀疏系统时,首尔大学开发的全堆芯输运计算程序nTRACER应用BICGSTAB算法求解CMFD线性系统,可降低并行矩阵向量乘积计算的耗时[2]。先进轻水反应堆模拟仿真联盟开发的中子输运程序MPACT中采用无Jacobian矩阵的Newton-Krylov方法,将非线性牛顿法和有限差分方法相结合代替Jacobian矩阵向量乘积[3]。我国自主开发的堆芯高保真中子输运计算程序HNET中应用GMRES方法求解CMFD线性系统,但在多核并行环境下,由于传统GMRES算法中点积的计算比矩阵向量乘积计算更加耗时,所以CMFD的加速效果受到限制。例如,用标准的并行GMRES方法求解C5G7-3D多群CMFD线性系统,当计算核数为768时,全局通信用时高达GMRES求解总时间的95%[4]。因此,减少点积计算引起的全局通信用时是GMRES方法并行算法设计与实现的研究重点。s步GMRES方法通过减少内积次数可实现算法优化[5-6],但该方法的数值稳定性较差,且计算和全局通信连续执行,处理器在通信阶段处于空闲状态,会造成处理器计算资源浪费。本文采用流水线思想[7],重构GMRES算法,实现每次迭代仅一次全局通信,并以最大限度的计算任务隐藏全局通信造成的延迟,充分利用处理器的资源,开发了流水线式并行GMRES求解算法及线性求解器。数值结果表明,流水线式并行GMRES求解器的并行计算效率大大提高,可有效加速CMFD线性系统的求解。
1 求解CMFD的标准并行GMRES算法
1.1 并行GMRES算法特性分析
GMRES算法通常用于求解非对称线性方程组,可在一定迭代步数后将残差降到最小。并行GMRES算法涉及的主要计算包括矩阵向量乘积(SpMV)、向量点积(dot product)、向量校正(AXPY)及预处理。
CMFD方法的并行实现基于区域分解,矩阵向量乘积(通常包括预处理部分)仅涉及相邻子区域之间的数据交换,在相邻的处理器之间进行通信,因此,矩阵向量乘积不会造成使性能严重降低的通讯问题。向量校正不涉及处理器之间的通信,而向量点积的并行计算需要来自每个结点、每个计算核的信息,是一个全局通信的过程,需要所有处理器保持同步。随着并行核数的增加,全局通信的用时越来越大,对算法的并行可扩展性产生严重的负面影响,点积计算引起的全局通信成为限制并行GMRES算法的主要因素。
1.2 Gram-Schmidt正交化方法
GMRES算法利用Gram-Schmidt方法构造标准正交基,为提高数值稳定性,常用修正的Gram-Schmidt方法(MGS)取代经典的Gram-Schmidt方法(CGS)。基于MGS的GMRES算法(MGS-GMRES)为
1)r0=b-Ax0
3)fori=0,…,m-1,do
4)w=Avi
5)forj=0,…,i,do
6)hj,i=(w,vj)
7)w=w-hj,ivj
8)end for
12)对Hi+1,i应用Givens变换
13)end for
14)xm=x0+Vmym,其中,ym是使‖Hm+1,mym-‖r0‖2e1‖2最小的解。
该过程中,进行点积运算的w向量在内迭代过程中不断更新,且只有得到更新后的w向量才能进行下一次点积运算,因此,对于第m次迭代正交化过程,需要逐次进行m+1次点积运算。在并行环境下,这意味着要进行m+1次全局通信,造成巨大的通信用时,因此,MGS-GMRES算法不适用于多核并行计算。MGS-GMRES算法在4个处理机上的迭代过程,如图1所示。其中,绿色表示本地计算,在典型的并行实现中不需要处理机之间进行通信;蓝色表示矩阵向量乘积计算,只需要相邻处理机之间进行通信;红色实线表示全局通信。

图1 MGS-GMRES算法在4个处理器上的迭代过程Fig.1 Schematic representation of a single iteration of the MGS-GMRES algorithm on four processors
CGS方法在正交化过程中的点积运算彼此独立,不存在数据相关性。通过合理的算法设计,首先进行局部点积运算,然后将每次点积运算需要传递的数据合并,提高通讯粒度,进而通过一次全局通信得到正交化部分所有点积的计算结果,极大地降低了全局通信的次数。针对CGS方法的不稳定性,可以采取迭代CGS方法进行改善[8]。本研究中采用重启动GMRES算法提高计算精度和稳定性,保证基向量的正交性,测试表明,效果良好。
2 并行GMRES算法的优化
2.1 集中点积的计算
基于CGS的GMRES算法(CGS-GMRES)进行程序设计,实现正交化部分点积合并计算。CGS-GMRES算法正交化与标准化过程点积计算之间存在数据依赖性,本质上是串行过程,因而正交化部分与标准化部分的点积计算不能进行合并。分析每次迭代过程发现,通过算法重构可以将一次迭代正交化过程包含的点积与上一次迭代标准化过程中的点积集中进行计算,从而实现1次全局通信得到所有点积计算结果。该算法的主要过程为
fori>0,


1)forj=0,…,i-2,

7) forj=0,…,i-2
9)end for


A2vi-1=Azi
(1)
(2)
Hessenberg矩阵元素的计算可表示为
hj,i-1=(Avi-1,vj)=(zi,vj)=
(3)
(4)
(5)
2.2 非阻塞通信
大规模并行计算环境下,全局通信耗时巨大,在阻塞通信结束之前,各个计算核心必须等待同步通信结束才能进行下一项工作,因此,浪费了计算资源。流水线技术是高效率利用硬件资源的经典方法,当不同阶段需要不同资源时,多任务重叠可以同时利用不同资源[9]。本文采用流水线思想,应用非阻塞通信,将通信任务交给特定的通信硬件去执行,在该通信硬件进行通信操作期间,充分应用各个计算核心的计算资源,处理与该通信无关的计算任务,提高程序执行效率。
非阻塞通信,一般需要调用2个MPI函数。首先要启动非阻塞通信,但启动并不代表该通信过程的完成。为了确保通信的完成,还必须调用与该通信相关联的通信完成接口,如MPI_Wait或MPI_Test,以等待或查询非阻塞通信是否完成,完成了检测调用才真正将非阻塞通信完成。
2.3 并行GMRES算法优化
采用非阻塞通信方式,在确保程序正确性的基础上,调整程序各部分执行的先后顺序,确保尽早启动和尽晚结束非阻塞通信[10]。用最大限度的计算任务屏蔽通信延迟,充分利用处理机通信期间的空闲等待时间。
本文基于已有的GMRES求解器,采用MPI并行编程模型,对重构算法部分程序执行顺序进行调整,将第m+1次迭代的矩阵向量积计算调整至第m次迭代点积计算后进行。先发出点积计算非阻塞通信组归约命令,即调用MPI_Iallreduce函数,后进行下一次迭代矩阵向量乘积的计算,完成计算后再调用MPI_Wait函数,等待非阻塞通信的完成。这样上一次迭代还未结束,下一次迭代已经开始,2次迭代在时间上重叠了一部分。改进的流水线式并行GMRES算法简称为p1-GMRES算法。其中,p代表流水线,1表示在执行非阻塞组归约的同时进行一个矩阵向量乘积的计算。
应用非阻塞组归约操作,将2次迭代融合。图2为流水线式并行GMRES算法迭代示意图。虽然每次迭代构造标准正交基的用时未发生变化,但以流水线的方式工作,减少了总的求解时间。

图2 流水线式并行GMRES算法迭代示意图Fig.2 Schematic representation of pipelineparallel GMRES algorithm iteration
3 数值结果
3.1 计算平台及测试算例
数值试验均在“天河一号”超算平台上进行。选取C5G7[11]及VENUS2[12]2个基准例题为研究对象,分别构建相应的3维多群CMFD线性系统。
3.2 数值分析
图3给出了GMRES求解计算时间t随核数N的变化关系。由图3可见,p1-GMRES算法具有较高的计算性能,GMRES求解计算时间明显减小。

(a)C5G7 benchmark problem
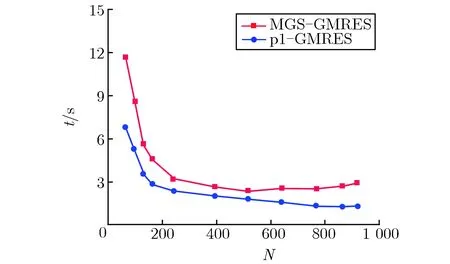
(b)VENUS2 benchmark problem
p1-GMRES算法和MGS-GMRES算法求解CMFD的用时对比,如表1所列。

表1 p1-GMRES算法和MGS-GMRES算法求解CMFD的用时对比Tab.1Comparison between p1-GMRES algorithmand MGS-GMRES algorithm for CMFD
由表1可见,在N<392时,即MGS-GMRES加速效果达到峰值前,p1-GMRES算法求解CMFD的用时比MGS-GMRES算法的用时减小约35%,可以有效加速CMFD线性系统的求解。
定义加速比SN为同一算法在单个计算核心上的运行时间与在N个计算核心构成的并行系统上的运行时间之比[13],即
(6)
图4给出了并行计算的加速比。由图4可见,p1-GMRES算法具有较高的加速比。对于C5G7基准题的CMFD线性系统求解,MGS-GMRES算法在核数为128附近加速比达到峰值,此后随着核数增加,加速比呈现下降趋势,运行时间逐渐增加;而p1-GMRES算法在核数大于128后加速比仍在增大,直到核数为416附近加速比达到峰值。对于规模更大的VENUS2基准题的求解,MGS-GMRES算法在核数为512附近加速比达到峰值;而p1-GMRES算法在核数为864附近加速比达到峰值,极大地提高了加速比。

(a)C5G7 benchmark problem
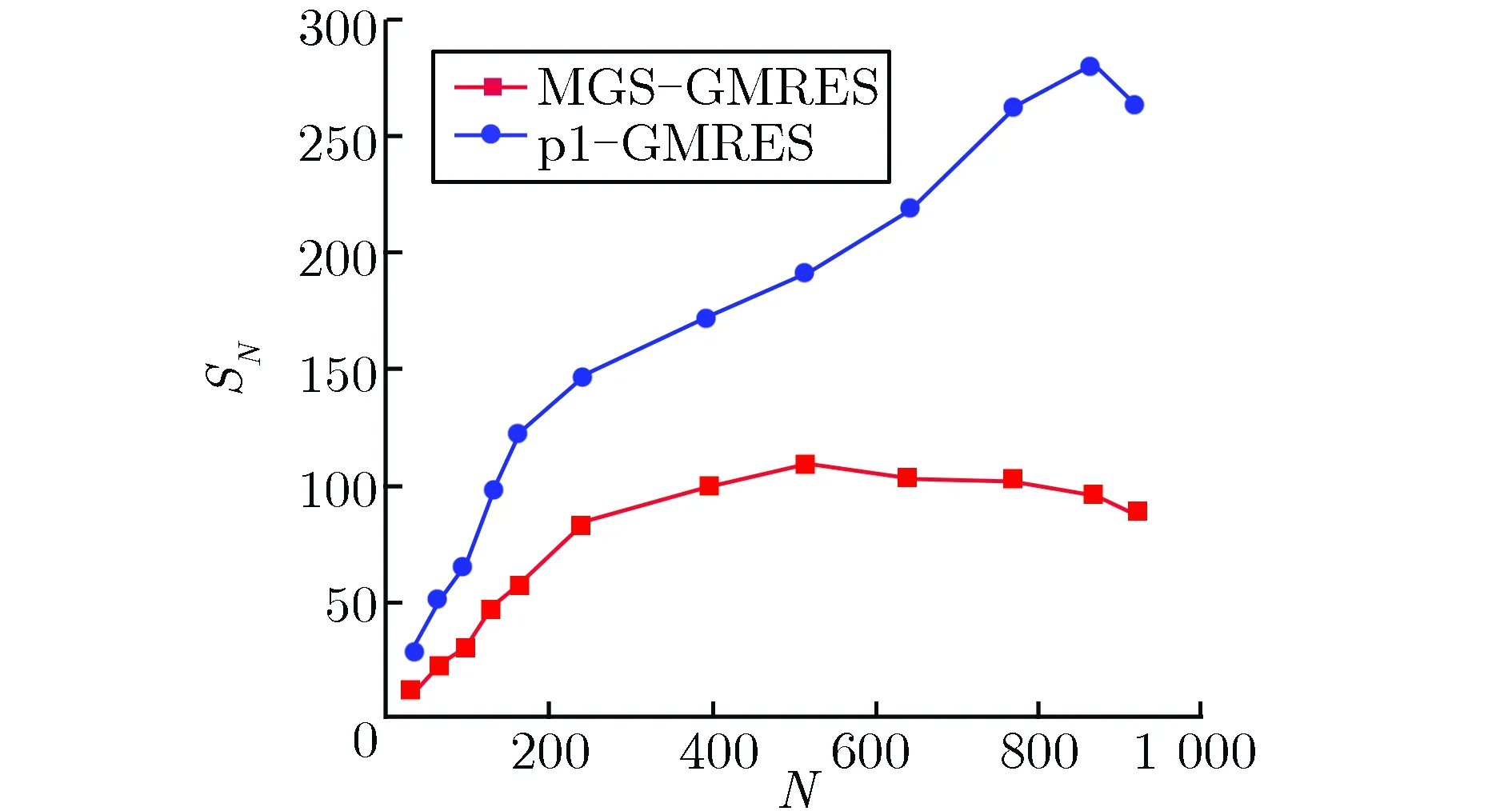
(b)VENUS2 benchmark problem
以稍微增加计算时间为代价,降低全局通信次数,并将全局通信与矩阵向量乘积的计算重叠,从而将全局通信用时降为最低。以求解C5G7基准题的CMFD线性系统为例,图5给出了并行GMRES算法各部分的执行时间。
由图5可见,p1-GMRES算法重叠计算后的全局通信用时比MGS-GMRES算法大大降低;而且,随着核数的增加,计算时间逐渐降低,全局通信用时逐渐增加,当加速计算的时间小于全局通信增加的时间时,运行时间开始增加。结合图3可知,随着核数增加,计算用时呈反比例关系迅速下降。与MGS-GMRES算法相比,在核数为768时p1-GMRES算法增加的计算量很小,且远远小于降低通信时所获得的时间收益。

(a)N=224

(b)N=392

(c)N=512
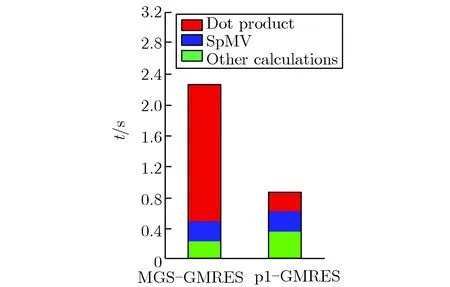
(d)N=768

(e)N=864

(f)N=918
并行效率反映一个计算核心的计算能力被有效利用的比率。并行效率的表达式为
(7)
表2给出了MGS-GMRES算法和p1-GMRES算法并行效率的对比。由表2可见,在对 C5G7基准题计算中,核数为128时,p1-GMRES算法的并行效率高于50%,而MGS-GMRES算法的并行效率小于30%;对规模更大的VENUS2基准题计算中,核数为224时,p1-GMRES算法的并行效率高于60%,而MGS-GMRES算法的并行效率小于35%。表2数据表明,p1-GMRES算法的并行效率显著提高,改进的流水线式并行GMRES求解器可以高效地利用处理器的计算能力,具有良好的可扩展性。
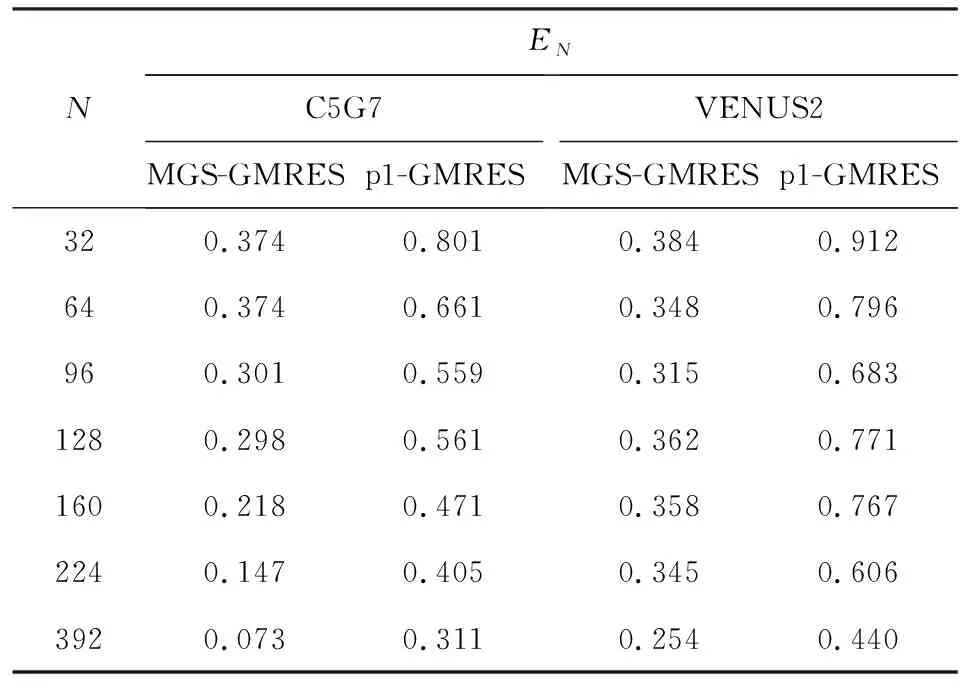
表2 MGS-GMRES算法和p1-GMRES算法并行效率的对比Tab.2Comparison of parallel efficiency betweenMGS-GMRES and p1-GMRES
4 结论
本文对并行GMRES方法中通信用时最长的向量点积并行计算进行了深入研究,采用MPI非阻塞通信方式,优化和重构了GMRES算法,提出了一种改进的流水线式并行GMRES算法,提高了通信粒度,开发了线性求解器,并将其成功耦合于精细化中子物理计算程序HNET中。以C5G7和VENUS2的3维CMFD线性系统求解为例,对MGS-GMRES算法与p1-GMRES算法的运行时间、加速比及并行效率进行了对比分析。数值结果表明,改进的流水线式并行GMRES算法极大地降低了向量内积并行计算对并行性能的影响,具有更高的加速比和并行效率,计算时间更短,可扩展性良好,实现了加速求解CMFD线性系统的目的。

