工业X射线检测图像预处理的研究进展

(洛阳欣隆工程检测有限公司 ， 河南 洛阳 471012)

随着科学技术和工业技术的迅速发展，近年来我国对铸造产品需求在数量和质量上都有大幅度的提升。铸件在出厂前几乎都需要对其进行无损检测以保证产品质量。如今，无损检测技术已在航空航天、石油化工、机械制造等领域得到了广泛的应用。

目前，射线检测技术在生产中的应用所占比例约40%，可见，射线检测仍然是十分重要的检测方法。传统的X射线检测技术是基于胶片成像和人工测评胶片，但这种方法存在工作效率低、人为客观因素影响大、无法实时成像、成本高以及图像管理不便等缺点。X射线实时成像及计算机图像处理技术结合了计算机数字图像处理技术与光电转换技术，可以通过图像增强将X射线图像转换为视频图像，再对图像进行数字化处理，以提高检测灵敏度和缺陷的识别能力，再利用计算机分析处理检测结果，进行检测结果评定，检测图像可长期在计算机或者光盘中进行保存，从而可使X射线检测实现自动化[1]。

一般情况下X射线原始检测图像灰度区间窄、对比度低、噪声多、缺陷边缘不清晰、缺陷特征被淹没、存在较大的背景起伏等缺陷，进而影响了无损检测人员对工件进行缺陷评定。图像预处理的目的主要是减少图像中的噪声，提高图像对比度，进而增强图像中缺陷的可识别性[2]。因而，有必要对检测图像的预处理进行研究，以提高检测图像质量。

1 检测图像的去噪处理

对检测图像的平滑处理技术进行研究的目的是消除噪声对检测图像影响的同时不会模糊检测图像的边缘轮廓[3-5]。目前，常用的去噪方法为空域法与频域法[6]。所谓频域滤波就是在一个频域内乘以一个滤波函数H(u，v)，频域滤波的处理的运算量较大，且图像的灰度区间较窄，灰度值小，限制了频域滤波的应用。

空域法滤波是借助模板在图像空间进行邻域操作完成的，可分为线性滤波和非线性滤波[7-8]。具体操作步骤如下：①将模板在图中漫游，使模板中心与图中一个像素位置重合；②使模板上系数与下对应像素相乘；③求和；④将模板输出响应值赋给途中对应模板像素中心像素。

1.1 线性滤波器

线性滤波器分为两种，即低通(平滑)滤波器与高通(锐化)滤波器[9]。低通滤波器可有效削弱或者消除傅里叶空间的高频分量而不影响低频分量，从而平滑图像；高通滤波器能够有效减弱或消除傅里叶空间的低频分量而不影响高频分量，从而锐化图像。

线性滤波器的基本思想是通过平均运算一点和其邻域来去除突然变化的点，从而去除噪声，但方法的缺点是图像会有一定的模糊。一般情况下模板不允许移除边界，因此经过处理后的图像会小于原图像。

采用尺度为s(M×N的矩形窗)的模板对f(x,y)进行运算，平滑处理后的灰度值如下：

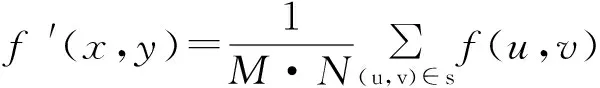
(1)

由式(1)可看出，模板尺寸的增大有助于噪声的消除，同时也会导致图像变得模糊。这就需要一个合适的阈值来减少邻域平均所导致的模糊效应。

高斯滤波前后图像对比如图1所示，从图1可看出，模板运算时，在去噪的同时会导致边缘细节的破坏[10]。

图1 高斯滤波前后图像对比

1.2 非线性滤波器

中值滤波是非线性滤波方法的一种，运算过程无需图像的统计特征，大幅度地简化了图像处理[11]。中值滤波并不会像线性滤波一样模糊图像细节，可保留图像边缘细节。中值滤波采用像素点邻域灰度值中值取代该点像素值。该方法对滤波脉冲的干扰、图像扫描噪声孤立点和线段的消除十分有效，而对消除高斯噪声的效果不佳。中值滤波并不适用于点、线、尖角较多的图像。目前常用的滤波有迭代中值滤波、加权中值滤波等。

中值滤波器可表示为：

g(x,y)=median{f(x-k,y-l),(k,l)∈W}

(2)

式(2)中g(x,y)噪声去除后的图像，f(x,y)为输入的原图像，W为二维模板，k模板长度，l模板宽度。

滤波效果很大程度上依赖中值滤波器窗口的尺寸及形状。中值滤波器窗口形状主要有线形、方形、圆形、十字形以及环形。较长缓变轮廓的图像常采用方形窗口。而存在尖角的图像常采用十字性窗口。一般从大到小逐步进行窗口尺寸的选择，直至滤波效果达到令人满意的效果。检测图像滤波前与滤波后的图像对比见图2。由图2中值滤波前后的对比如图可知，中值滤波可进行有效降噪，而不影响图像的轮廓[12]。

图2 检测图像滤波前与滤波后的图像对比

2 检测图像对比度的增强

射线检测图像的灰度大多数在一个很窄的区域内集中，会导致图像的观察困难。因此为扩大图像的灰度范围，需要对检测图像中每个像素的灰度进行灰度标度变换。目前还没有统一的图像增强理论，关于图像质量的衡量的客观标准也没有[13-17]。

2.1 灰度变换

2.1.1线性变换

线性变换有两种变换方式，分为全域线性变换与分段线性变换。全域线性变换为对全部像素同时乘以相同的系数，对全部像素做相同倍数的增大或者减小。分段变换为对检测图像感兴趣区域的灰度进行拉伸来改善图像质量。检测图像中灰度不明显区域的灰度通过拉伸或压缩，可改善检测图像的视觉效果。常用的分段拉伸方法是三段线性拉伸，其表达式如公式(3)所示，示意图如图3所示[18]。

(3)

公式(3)中f(x,y)为点(x,y)变换前的灰度值，g(x,y)为点(x,y)变换后的灰度值。

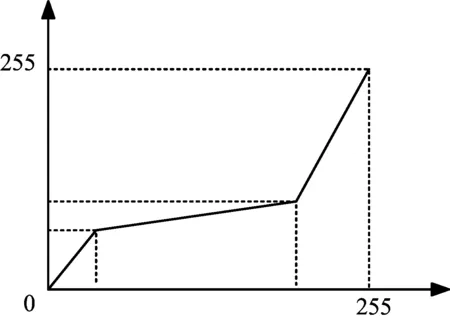
图3 检测图像灰度拉伸原理

使用分段线性灰度变换拉伸检测图像偏暗的灰度区间进而改善图像。如果使用分段线性灰度变换压缩检测图像偏亮的灰度区间进而改善图像。三段线性拉伸示意图如图4所示[19]。

2.1.2非线性变换

所谓非线性变换是指按照要求的非线性变换对检测图像进行变换，从而突出缺陷，淡化图像背景，改善检测图像质量。例如，有时需要在中间灰度级有较多的扩展，以便把在灰度级中间的缺陷凸显出来，而灰度范围两端有较少的扩展。

图4 三段性灰度拉伸图

非线性灰度变换常采用的函数有对数函数、指数函数及平方函数等非线性函数。非线性变换前后的检测图像对比如图5所示[10]。

图5 非线性变换前后检测图像对比图

2.2 直方图均衡化

把给定的直方图改变成均匀分布的直方图就叫做直方图的均衡化，也被称作灰度均衡[20]。均衡化后的直方图会增加检测图像的对比度。直方图经过均衡化处理后是近似均匀分布的，图像具有离散的灰度。

图像经直方图均衡化后检测图像的灰度动态范围及量化层间隔都会有多扩大，灰度级别会减少，因此有可能会导致轮廓的出现。

图像目标处与背景过渡处像素点较少，均衡化可把较少像素的灰度合并变成背景点或者目标点，进而使边界处变得陡峭。图像目标处与背景过渡处像素点较多，均衡化会增加像素灰度间的差距，进而增大背景和目标的对比度。

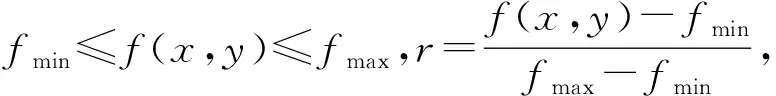
(4)

公式两端同时积分可得：

(5)

也就是说T(r)为函数Pr(r)的分布累计函数。

在检测数字图像中灰度是离散的，离散化直方图均衡公式可表示为：

(6)

式(6)中rk∈[0,1]，sk∈[0,1]，k离散灰度级，sk取值为T(rk)最近的灰度值。

图像实际显示时，可用公式(6)计算sk变换后的非正规灰度，即：

lk=‖sk×(fmax-fmin)+1‖

(7)

公式(7)表示四舍五入取整数。对检测图像进行均衡化后的效果如图6所示[8]。

图6 均衡化前后图像对比

3 结语

X射线图像的降噪与对比度增强作为图像预处理的重要环节，其效果直接决定检测图像的质量。图像的预处理方法都是具有一定的针对性，通用的预处理算法并不存在。本文主要介绍了X实时成像预处理的几种方法。非线性中值滤波在图像降噪方面的效果较好。直方图均衡化在对比度增强方面的效果较好。