一类带延迟项粘弹性方程的初边值问题的爆破

郑雅匀， 杨 晗， 李 莎

（1.电子科技大学 成都学院，成都611731；2.西南交通大学 数学学院，成都611756）

0 引 言

在初始能量为负的情况下，利用凸方法得到解的爆破情况。当1＜m＜∞，p满足条件（A2），且p＞m时，初始能量小于E1（其中E1的定义参见文献［3］中的引理2.3）时，构造爆破因子得到解的爆破。文献［3］不但考虑了文献［2］的初始能量为负的情况，还考虑了初始能量有上界的情形。在方程（4）的基础上，当不考虑非线性阻力项时，文献［4］研究了欧拉-伯努利粘弹性方程：

1 主要结论

首先给出初始能量为负的爆破情形。

其次给出初始能量为正的爆破情形。

定理2 假设记忆项满足条件（A1），源项指数p满足条件（A2），初值u0∈H20（Ω），u1∈L2（Ω），且

2 准备工作

引入一个新的函数

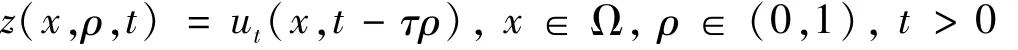
显然，

则可将问题（1.1）改写成：

3 主要结论的证明