一类A型仿射李超代数的Z-阶化超双导子

韩纪蕊， 远继霞

（黑龙江大学 数学科学学院，哈尔滨150080）

0 引 言

李代数的研究主要分为两个方面：结构理论和表示理论。导子的研究是李代数结构理论中不可缺少的一部分。在文献［1］中作者给出了导子的定义后，学者们相继对其进行了研究。在文献［2］中，作者证明了所有交换素环上的双导子都是内双导子。在文献［3］中，作者证明了有限维单李代数的导子是内的。在文献［4-5］中，作者研究了在自同构σ⊗τ（σ和τ分别是A和B上的有限阶自同构）下的不动点子代数的导子代数，对于仿射李代数L，得出结论D（L′）和D（L′/Z（L′）相似。李超代数是在李代数基础上发展起来的一个代数学分支，发展历程与李代数相似。在文献［6］中，作者探究了Heisenberg超代数超双导子的一些性质。在文献［7］中，作者证明了超Virasoro代数的超对称超双导子是内的。在文献［8］中，作者证明了所有的典型单李超代数的超双导子都是内的。在文献［9］中，作者对仿射李超代数进行了研究和分类，仿射李超代数分为扭仿射李超代数（见文献［10］-［12］）和非扭仿射李超代数（见文献［9］）。在文献［13］中，作者研究了仿射李超代数的超导子，本文将研究一类A型仿射李超代数的Z-阶化超双导子。

1 预备知识

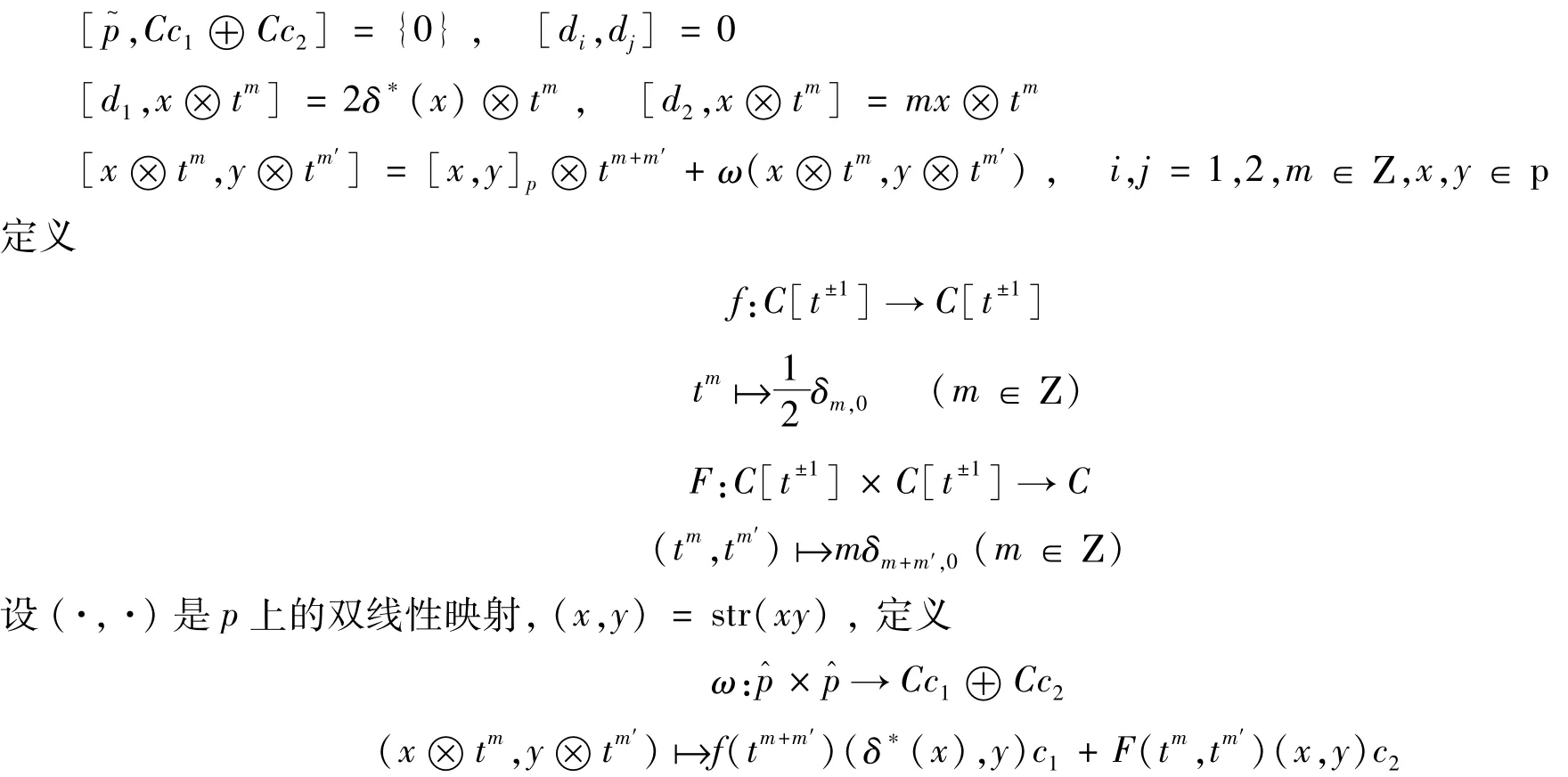
2 仿射李超代数p～的Z-阶化超双导子