考虑初期支护作用的引水隧洞衬砌结构配筋计算
许 韬,戚绍礼,胡天明,殷子文
(1.中国电建集团成都勘测设计研究院有限公司,四川成都610072;2.中国水利水电第七工程局有限公司,四川成都610213;3.河海大学,江苏南京210098)
0 引 言
尽管有许多学者对围岩和衬砌结构的联合受力开展了大量的研究工作[1- 4],也取得了一些成果,但目前,我国水工高压隧洞设计规范中并未考虑围岩和初期支护的承载作用[5]。初期支护作为安全储备,设计过于保守,往往导致二次衬砌结构断面尺寸偏大,配筋量增大[6]。随着施工期安全要求的提高,在施工过程中,现场往往会采取超强的临时支护措施,如果在这种情况下,仍然不考虑初期(临时)支护的作用,势必造成工程投资的无谓增加,影响施工。因此,在工程设计过程中适当考虑临时支护的作用是必要的,也是贯彻工程设计“既安全又经济”原则的主要做法。本文结合固增水电站引水隧洞施工过程揭露的地质现象,进行了围岩参数反分析,开展了考虑临时支护措施的衬砌结构受力分析,对衬砌配筋进行了优化。
1 工程概况
某水电站采用引水式开发方式,工程枢纽由拦河闸坝、进水口、引水隧洞、调压室、压力管道、地面发电厂房组成。压力引水隧洞沿木里河左岸布置,引水线路长11.06 km,平面上共设置5个转点,纵坡i=2.086 9‰。引水线路位于高山峡谷地貌区,地形高差悬殊,沿线沟谷深切,多呈不对称的“U”和“V”形谷,植被较发育。隧洞沿线支沟较为发育,从上游到下游发育规模较大的冲沟有洼开沟、撒洼沟,沟内常年性流水,洪水期流量较大。隧洞区围岩分类原则以岩性为基础,结合地质构造的发育情况,按DL/T 5410—2009《中小型水力发电工程地质勘察规范》围岩工程地质分类标准,将隧洞区围岩划分为Ⅲ、Ⅳ和Ⅴ共三类,本次计算以Ⅳ类围岩为例开展分析。
引水隧洞马蹄形开挖马蹄形衬砌,过流断面尺寸为6.1 m×7.8 m(底宽×高),并根据围岩类别采用不同的支护形式和衬砌厚度。引水隧洞沿线垂直埋深一般为150~400 m,本次计算断面埋深320 m。
2 分析理论与方法
2.1 本构模型
围岩分析计算采用经典的传统弹塑性模型,屈服准则采用ABAQUS自带的D-P准则(或霍克-布朗准则),即M-C外角点外接圆准则。D-P系列屈服准则是在Mises强度准则的基础上,考虑平均应力p或I1,而将Mises强度准则推广成为以下形式:
(1)
式中,I1为应力张量的第一不变量;J2为应力偏量第二不变量。α与k为与岩石内摩擦角φ和粘结力c有关的实验常数,可由下式计算得到
(2)
(3)
2.2 配筋计算方法
根据相关材料整理部分计算所需数据:按照运行工况下,即衬砌所受拉应力最大截面分析,顺水流方向长度取1 m。混凝土强度等级为C25,fcd=12.5 MPa,钢筋等级采用HRB400(fsd=f′sd=360 MPa,ξb=0.518)。取保护层厚度as=35 mm,则截面有效高度为h0=h-as。
对于隧洞结构,可以将应力转换成内力,按照截面破坏内力来计算钢筋用量。并假定构件破坏时截面全部裂通,拉力全部由钢筋承受,按照受拉构件计算。
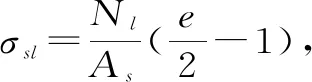
γdNe≤fsdAs(h0-a′s)
(4)
故所需钢筋面积
(5)
式中,AS为所需钢筋面积;γd为钢筋混凝土结构的结构系数;N为截面所受轴力;h为截面高度;as和a′s为截面两端保护层厚度;fsd为钢筋抗拉强度;h0为截面有效高度。
3 有限元模型建立
3.1 几何模型与边界条件
计算选用典型断面建立三维模型,模型上下左右边界距离洞轴线各50 m。隧洞沿水流方向长度取120 m。模型中衬砌剖分4层网格,喷射混凝土剖分1层网格,灌浆圈厚4.5 m,分为5层,灌浆圈和喷射混凝土层之间设置过渡薄层。有限元分析计算网格模型见图1。选用OXYZ坐标系,模型左下角为坐标原点,其中,X方向为垂直水流方向,Y方向为洞轴线方向,Z方向为竖直方向。模型底部固定x,y,z方向位移,左右侧固定x方向位移,前后侧固定y方向位移,顶部为自由面。模型顶部施加对应埋深处的自重应力,来模拟上部荷载。
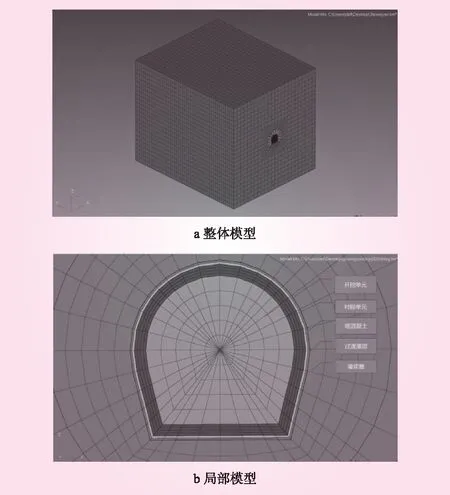
图1 有限元计算网格模型

图3 围岩开挖围岩位移云图(单位:m)
3.2 计算参数
(1)材料力学特性参数。岩土力学参数的合理性与否是进行岩土工程稳定性分析的关键环节。本文根据位移监测资料运用智能优化方法进行参数反演,并将遗传算法融入到反演分析的过程当中,编写了相关的遗传算法的Fortran源程序;以此对ABAQUS软件进行了二次开发,并基于所建立的反分析模型对围岩参数开展了反演分析研究。选取计算对应的典型断面4+852的监测数据开展反分析,如图2所示,所得围岩参数见表1。
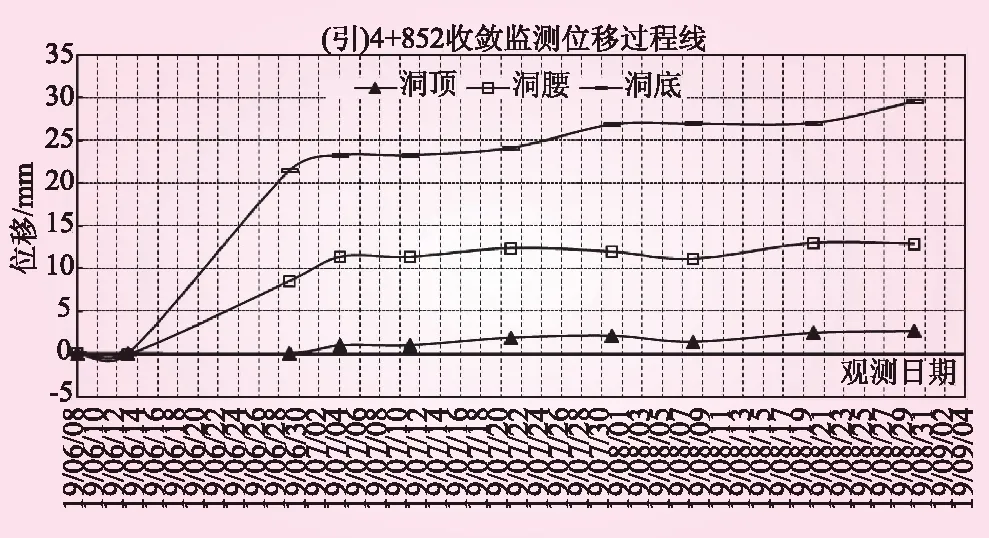
图2 典型断面监测数据(2019年)
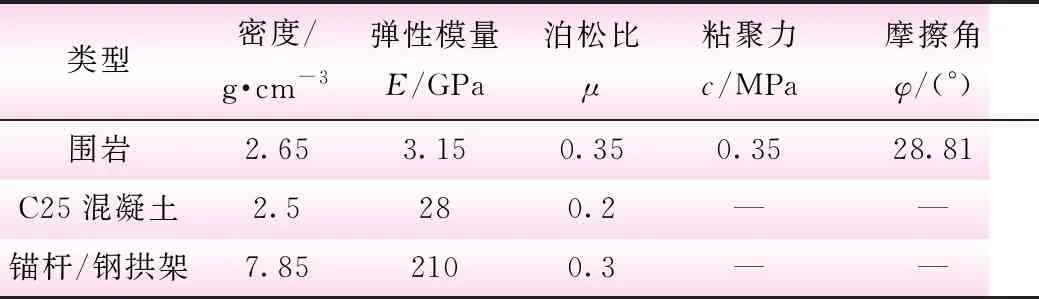
表1 计算模型力学参数
(2)支护参数。计算选用的支护参数由设计院提供,具体如下:喷混凝土12 cm,钢筋混凝土衬砌厚度40 cm;锚杆采用Φ25型号,长4.5 m,间排距1.5 m;工字钢采用I16型号,间距1.5 m;在顶拱120°范围内进行回填灌浆。
3.3 计算工况
本次计算共选取了施工期、检修期和正常运行3个工况。其中,施工期重点考虑了回填灌浆压力、山岩压力等荷载;检修期主要考虑了外水压力、山岩压力、结构自重等荷载;正常运行期主要考虑了内水压力、山岩压力、结构自重等荷载。经计算,结构配筋控制工况为正常运行工况,因此,本文均以该工况进行整理说明。
4 成果分析
本文对有无初期支护两种情况下的围岩稳定性和衬砌结构受力特性进行了分析计算。
4.1 围岩稳定性分析
围岩稳定性判别主要以相对位移和塑性区开展深度为判定依据,判断围岩稳定性。位移值为“+”表示竖直向上,为“-”表示竖直向下。
洞室开挖后,围岩变形主要以竖向位移为主,具体见图3。由图3可知,洞室底部有上升趋势,顶拱则是下沉。在没有任何支护措施的情况下,最大竖向位移为5.31 cm。施加支护后,最大位移为3.19 cm。
洞室施工完成后,部分岩体发生塑性变形,如图4所示。从图4可以看出,洞周两侧是塑性区较为集中的部位。隧洞顶部和底部并未进入塑性状态。裸洞开挖时塑性区范围较大,开展深度约为2.5 m;施加支护后,开展深度减小到1.3 m左右,为保证岩体稳定,应加强隧洞两侧的支护措施。
计算结果表明,施加初期支护后,围岩变形、应力有了很大改善,塑性区范围也明显缩小。因此,施加初期支护可以提高围岩自身的承载能力,减小围岩变形,提高围岩的稳定性,从而加强围岩在运行期内水压力作用下的承载比,减少衬砌受力。
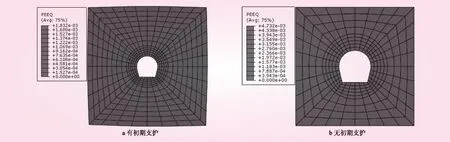
图4 围岩开挖塑性区分布

图5 运行期无支护衬砌受力(单位:kPa)

图6 运行期有支护衬砌受力(单位:kPa)
4.2 衬砌结构受力分析
运行期隧洞内充水,衬砌在内水压力作用下,应力以受拉为主。以下仍按照有无初期支护两种情况来分析衬砌受力。
无初期支护时,衬砌受力以垂直水流方向为主,最大拉应力出现在边墙底板交接处,应力集中。顺水流方向最大拉应力为0.69 MPa,垂直水流方向最大拉应力为2.56 MPa。应力云图见图5。
有初期支护时,衬砌受力以垂直水流方向为主,最大拉应力出现在边墙底板交接处,应力集中。施加初期支护后,应力数值有所改善,顺水流方向最大拉应力为0.49 MPa,垂直水流方向最大拉应力为2.10 MPa。应力云图见图6。
从计算结果可知,施加初期支护后,衬砌应力值得到了改善。其中,顺水流方向应力值较小,可按构造要求配置纵向钢筋;垂直水流方向应力值较大,超过混凝土设计强度,需要对其进行配筋改善结构受力。
4.3 衬砌结构配筋及裂缝开展宽度验算
(1)结构配筋。笔者根据衬砌受力情况计算出有无初期支护两种情况下的配筋结果,同时将设计院按照边值法计算的配筋成果一起比较发现,考虑围岩—衬砌联合受力的配筋量明显减小,且考虑施加初期支护后的围岩—衬砌联合受力情况下,衬砌结构配筋量更小。具体配筋情况如表2所示。
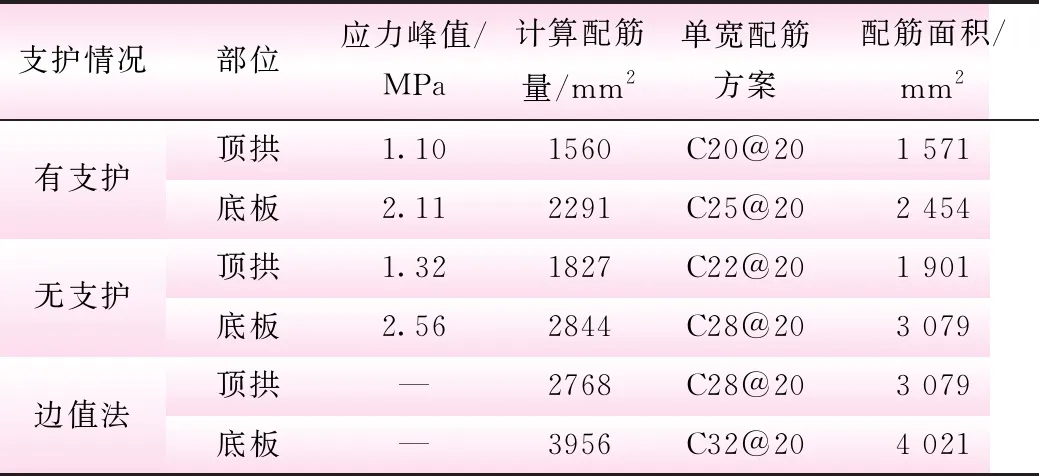
表2 衬砌结构环向配筋
(2)裂缝开展宽度验算。根据数值计算的配筋量,按照DL/T5195—2004《水工隧洞设计规范》中的附录公式计算衬砌裂缝宽度,Ⅳ类围岩取中值时衬砌的最大裂缝宽度为0.165 mm,发生在下侧拱与底板连接处,最大裂缝的宽度小于裂缝宽度允许值0.3 mm,满足规范要求。
5 结 论
本文以实际工程为例,采用数值方法模拟了水工隧洞的开挖和充水运行过程,通过对比有无初期支护两种情况下围岩稳定性和衬砌受力情况来对衬砌结构配筋进行计算。得到了如下结论:
(1)对于地质条件复杂,围岩参数无法准确给出的情况,可以利用参数反分析方法,根据施工过程中监测的位移数据进行反分析,从而获得较为实用的围岩参数。
(2)数值计算方法可以充分考虑围岩自身的承载能力和支护的作用效果,与工程实际相符,因此,有条件的情况下,可以采用数值分析方法开展地下工程的稳定性评价和衬砌结构配筋设计,作为工程建设的主要依据。
(3)计算结果表明,运行期是衬砌受拉应力最大时期,内水压力由围岩和衬砌共同承担。初期支护可以极大地提高围岩的承载能力,对比有无初期支护两种情况的配筋方案可以得出,施加支护后底板配筋量减少了30%左右。

