基于Gumbel Copula函数的堆石坝沉降模型因子优选研究
仲静文,朱 晶,周 健,顾 冬,刘永涛
(1.南京市水利规划设计院股份有限公司,江苏南京210022;2.南京新港开发总公司,江苏南京210038;3.河海大学水利水电学院,江苏南京210098)
0 引 言
面板堆石坝因其成本较低、施工快速方便、地形地质适应性强等优点迅速发展为一种重要的坝型[1]。面板堆石坝的沉降变形是影响其安全稳定的重要因素,故研究面板堆石坝的沉降,特别是施工期和蓄水期沉降以评估其安全状态就十分必要[2]。研究面板堆石坝沉降的模型和方法有很多,如传统的统计预测模型、智能算法模型、有限元计算模拟方法等。目前,研究学者们提出了大量智能优化算法的大坝沉降模型,如万臣等提出了基于新维BP神经网络-马尔科夫链模型的大坝沉降预测方法[3];朱创家等基于极限学习机分析预测了面板堆石坝施工期沉降[4];蓝善勇等构建了基于最小二乘法的逻辑回归的土石坝沉降预测模型[5]等。上述模型和方法在研究沉降问题上总体精度较高、适应性较好,但很多堆石坝沉降模型没有考虑每个影响因子的影响因素,如水位、时间、温度等因子,从而导致局部过拟合、计算结果精度不高。
影响因子的选择一般有相关系数法、逐步回归法、主成分分析法等。相关系数法要求变量之间线性相关,局限性大;逐步回归法挑选步骤繁琐,无法直接准确地将预选因子引入方程中;主成分分析法将多个变量降维后选取比重大的因子作为主成分进行分析,但因子之间相关性较差时误差较大[6]。为此,陈西江等采用不同相关系数法,基于BP网络进行大坝位移预报[7],但前期无效数据影响到预报稳定性;进一步,袁从贵等提出偏互信息(PMI)确定预测输入因子,同时联合最小二乘定尺度支持向量机进行咸潮预测[8];麦紫君等在传统构造模型的基础上,采用偏互信息(PMI)筛选与月径流相关性较强的气候因子,从而预测中长期径流[9]。通过研究多个偏互信息方法筛选效果,偏互信息法(PMI)不仅计算方便快捷、适应性强,对于因子的优选精度也已达到较高标准,且较少应用在堆石坝沉降因子优选。由于偏互信息法计算回归值时误差较大,对筛选正确率不利[10],因此本文以大坝沉降变形为例,采取双重因子优选:①根据Pearson及Kendall秩相关系数等方法,预选因子集;②分析二维Gumbel函数,采用基于PMI的Copula熵法,优选因子集,并将其引入方程中,对大坝沉降值进行拟合及预测。
1 基本原理
1.1 沉降统计模型
面板堆石坝的沉降位移中,固结所占比例较大,同时温度及水位等也有一定影响,而时效因子的性质部分由固结引起。故运行期沉降值由水压分量δH、温度分量δT和时效分量δθ组成,统计模型[11]为
(1)
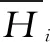
1.2 Gumbel Copula函数

H(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))
(2)
若边缘分布即F1,F2,…,Fn连续,则C唯一,否则,C在RanF1×RanF2×…×RanFn上是唯一的。
Copula函数中椭圆分布族和阿基米德分布族最为常见,而后者中Gumbel Copula函数的概率密度函数图形呈“丁”字形,呈现明显的上尾相关性,适合变量非对称变化,从而得到推广和应用。本文以二维Gumbel Copula函数为例,即
(3)
式中,u、v分别为两变量的边缘分布函数F(x)、F(y);α为参数,且α∈[1,∞]。
1.3 Copula熵理论
熵理论由Shannon提出解决随机变量不确定性的方法[13],多维联和熵为

(4)
考虑与大坝变形相关的二维随机变量情况
(5)
式中,f(x1,x2)为Copula函数的概率密度函数。
则分布函数及密度函数为
F(x;δ1,δs,θ)=C(F1(x1;δ1),F2(x2;δ2),θ)
(6)
f(x;δ1,δ2,θ)=c(F1(x1;δ1),F2(x2;δ2),θ)1f1(x1;δ1),f2(x2;δ2)
(7)
1.4 偏互信息
偏互信息由Sharma提出,为互信息的改进方法,可以估计大坝变形在预选因子基础上,新加入因子与变形值的相关性。具体如下

(8)
x′=x-E[x|Z];y′=y-E[y|Z]
(9)
式中,E为期望值,x为输入因子;y为输出值;Z为预选因子集。又H(x′,y′)=H(x)′+H(y′)+Hc(u′,v′),则PMI=-Hc(u′,v′)。
1.5 影响因子选择指标
1.5.1预选因子指标
Pearson相关系数及Kendall秩相关系数等是常用的度量变量相关性的方法,前者主要用来衡量两个变量的线性关系,后者基于Copula函数,用来描述变量之间的线性与非线性的相关关系[14]。后者方法具体如下

(10)
(11)

1.5.2因子优化指标
在计算出因子与输出值的偏互信息后,需要为PMI一个阈值作为确定最有因子的指标。本文采用Fernando等和May等研究成果,以Hampel检验作为PMI算法的停止准则[15-16]。具体如下
(12)

综上所述,模型因子集的确定步骤如图1所示。

图1 模型因子优选流程
2 实例分析
2.1 工程概况
某混凝土面板堆石坝位于我国东南地区,坝址以上流域面积667 km2,设计洪水位365.04 m。坝基最低部位高程274.20 m,坝顶高程368.0 m,坝顶长210.0 m。考虑到蓄水初期面板堆石坝常规统计模型的欠拟合情况,采用基于Gumbel Copula函数的大坝沉降位移模型,选取坝顶典型测点2及测点4、5、6进行计算。实测资料时间为1997年2月2日至2014年12月31日(监测频次为每月一次),预测资料时间选取2015年1月1日至2015年5月31日。本文以测点2为例进行分析。
2.2 模型因子优选
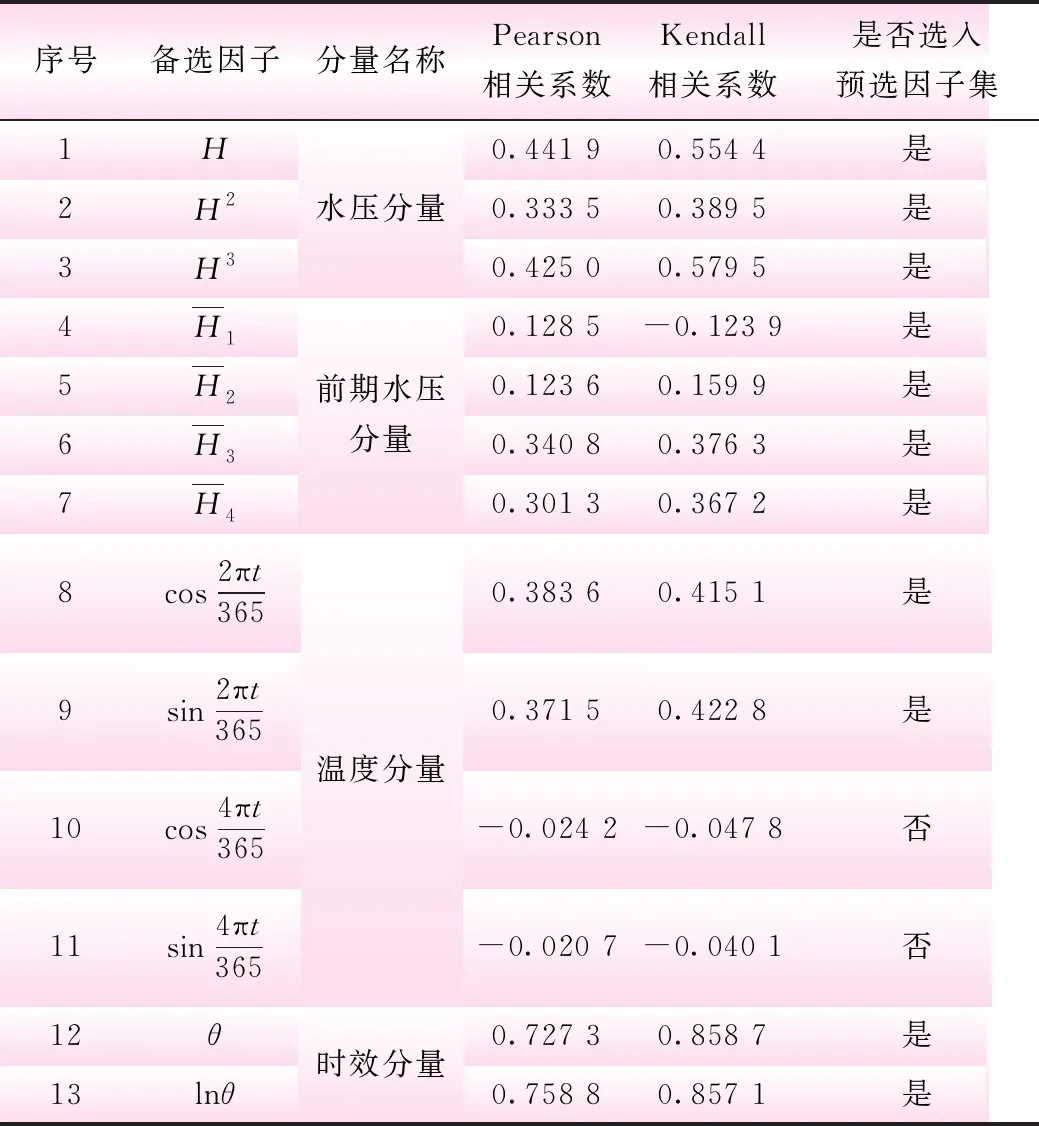
表1 预选因子集统计

2.3 结果对比
为了验证Gumbel Copula函数在大坝沉降模型中的可行性,对Copula熵优化后的模型与多元回归统计模型进行计算及对比分析,结果如表2、3及图2所示。

表2 测点的拟合结果对比

表3 2015年测点2沉降值预测结果及误差分析

图2 测点2沉降模型曲线拟合及预测情况对比
由表2可知,Gumbel函数模型的拟合效果明显优于多元回归模型,精度较高。经计算测点4、5、6沉降预测值的多元回归模型平均残差分别为4.5、4.14、3.68 mm,平均相对误差分别为3.97%、3.26%、2.81%;Gumbel函数模型的平均残差分别为2.10、1.66、1.62 mm,平均残差分别为1.85%、1.31%、1.25%。Gumbel函数模型预测沉降值的平均残差和平均相对误差明显小于多元回归模型。表3和图2的对比结果同样验证了Gumbel函数模型的拟合效果更优。
3 结 论
(1)本文建立了基于 Copula 熵的因子优选流程,对影响沉降的因子集采用了Pearson和Kendall双重相关系数进行预选,通过Copula熵理论进行筛选,提高了模型的稳定性,该方法为堆石坝沉降模型的因子优选提供了新思路。
(2)通过与常规模型的结果对比,基于Gumbel Copula函数的因子优选方法可以有效地筛选掉影响较小的因子,解决蓄水初期堆石坝拟合不佳的问题,降低了回归误差,提高了堆石坝沉降的预测精度,减小了计算工作量和复杂程度。
(3)由于采用的是二维Gumbel Copula函数,可以进一步研究高维Gumbel Copula函数在沉降模型的应用。

