集对分析在岩溶区流域水资源预测中的应用

莫崇勋，王亚芳，阮俞理，莫细喜，孙桂凯，麻荣永

(1.广西大学土木建筑工程学院，广西南宁530004； 2.工程防灾与结构安全教育部重点实验室，广西南宁530004; 3.广西防灾减灾与工程安全重点实验室，广西南宁530004)

0 引 言

水资源预测与分析是水资源合理开发利用的基础与前提。水资源预测方法有多种[1-3]，但是如何处理不确定性是目前需要解决的主要问题之一，而集对分析就是处理不确定性问题较为理想的方法。目前，集对分析在水资源预测方面已经有很多应用，如Feng等[4]将集对分析用于中国山都站新疆伊犁河进行水资源的预测，结果表明基于集对分析的拟合值与山都站年平均流量等级的实际值吻合较好，说明预测是有效的。Li等[5]应用小波去噪特性，利用汾河水库坝下站1959年～1989年的资料建立小波去噪SPA模型，通过对单一预测模型和水文预报与实测序列综合预测模型的对比，结果表明综合预测模型优于单一预测模型。卢家海[6]将集对分析应用于小浪底水库，对径流组合预测模型进行模拟，结果显示组合预测模型预测精度高于单个模型的预测。吴新新[7]将G-SPA预测模型应用于新疆黄水沟年径流量预测中并与GRNN神经网络模型以及AR(2)模型的预测结果进行对比，结果表明G-SPA模型的预测精度高于与GRNN神经网络模型以及AR(2)模型。李深奇等[8]将G-SPA预测模型应用于沱江三皇庙站，并与GRNN神经网络模型及AR(2)的预测结果对比，结果表明G-SPA模型预测精度偏高。刘玉晶等[9]将集对分析用于潘家口水库进行径流预测，结果表明该方法原理简单且实用性强，适合径流的中长期预测。

虽然集对分析在水资源预测中有一定成果，但大都是针对非岩溶区流域，而岩溶区流域因下垫面条件特殊，径流影响因素复杂，能否运用集对分析方法对岩溶区流域水资源进行预测是需要关注的问题。因此，本文以中国西南典型岩溶区流域-广西澄碧河流域为研究对象，用年径流量为评价指标，根据互相关系数统计假设检验和集对分析检验，确定影响水资源变化的主要物理因子。在此基础上，基于集对分析的同、异、反三个方面对影响预测水资源变化的主要物理因子与历史年的主要物理因子进行相似性分析，用多个最相似的历史样本径流量的加权平均值作为预测年径流量的预测值，然后根据预测结果评价集对分析方法的适用性，以资为岩溶区流域水资源调查评价提供帮助。

1 流域及资料

广西澄碧河流域总面积2 087 km2，其中岩溶区面积1 121 km2，占比为53.7%。流域内以高峰丛洼地和峰丛洼地为主要地貌特征，各种岩溶形态发育齐全，是中国南方较为典型的岩溶区流域之一。澄碧河流域内平塘水文站控制流域面积1 326 km2，占全流域面积的63.5%。资料采用1963年～2007年共45 a的平塘站径流、气温、蒸发量和降水数据；1963年～2007年的太阳黑子、多变量ENSO指数(MEI)、海洋尼诺指数(ONI)、北极涛动指数(AO)、南极涛动指数(AAO)、北大西洋涛动指数(NAO)；太平洋涛动指数(PDO)、东亚夏季季风指数(EASMI)、南亚夏季季风指数(SASMI)和南海夏季季风指数(SCSSMI)等10个气候因子。

2 方法简介

2.1 互相关系数统计假设检验原理

根据研究区域水资源的物理成因机制和统计关系，初选影响研究区域水资源yi的物理因子为{xij|j=1-m} ，i=1-n。其中n和m分别为样本容量和初选的物理因子数目。物理因子xij与水资源yi的互相关系数为[10]

(1)

根据抽样分布理论，当

(2)

则认为物理因子xij与水资源yi之间在统计上相关显著，否则它们在统计上相互独立[11]。式中，α为显著水平；tα/2为自由度n-2的t分布双侧检验的临界值；rmin为相关性显著所需的最低相关系数值。

2.2 集对分析原理

对不确定性系统中有关联的两个集合构成集对，对集对中某一特定属性做同一性、差异性、对立性分析，利用联系度描述集对的同、异、反关系[12]。

设有关联的集合X和Y，其中集合X和Y均有n项特性，即X=(x1，x2，…，xn)，Y=(y1，y2，…，yn)。X和Y构成集对H(X，Y)，描述H(X，Y)间关系的联系度定义为

(3)

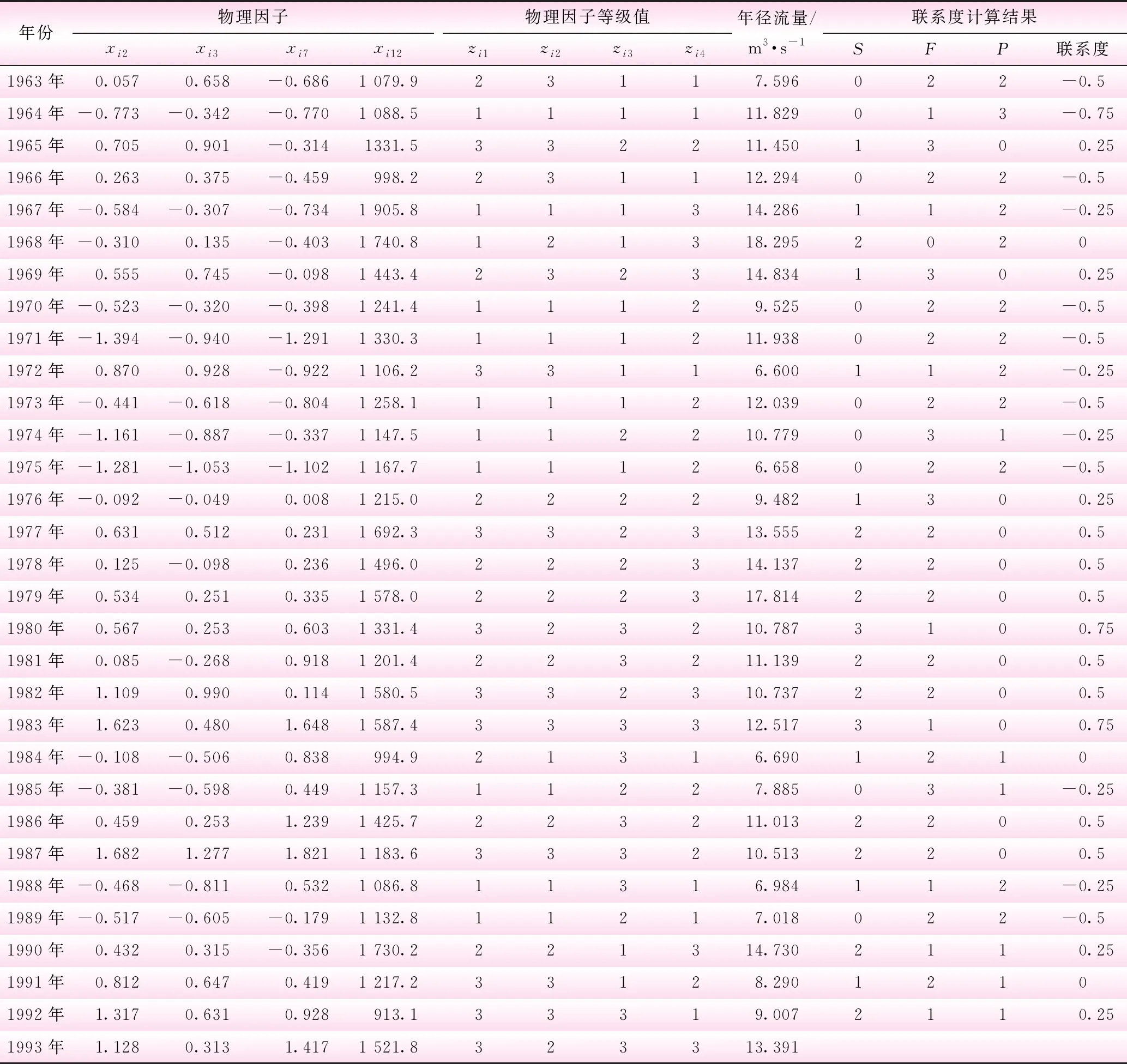
式中，S为集合X与Y对应的符号相同的个数；F为集合X与Y对应的符号相差一级的个数；P为集合X与Y对应的符号相差两级的个数；N为样本容量；I为差异度系数，在[-1，1]取值；J为对立度系数，一般恒取-1；a、b、c分别为集对H(X，Y)的同一度、差异度、对立度，且a+b+c=1。在联系度uX-Y中，a、b、c分别为集合X与Y中变量之间相关结构中存在正相关趋势、既非正又非负的不确定性的相关关系以及负相关关系；a>c表示变量之间存在正相关关系，a

b<0.50

(4)

则表示这种正相关或负相关关系是相对确定的，否则是不确定的。

显然，联系度uX-Y∈[-1，1]。若集合X与Y间的差异性越大，则uX-Y越接近于-1，表示这两因子集越倾向于不相似性；若这两因子集间的差异性越小，则uX-Y越接近于1，表示这两因子集越倾向于相似性。可见联系度uX-Y就是可变模糊集“X与Y间的相似性”的一种相对差异度函数。于是该模糊集的相对隶属度函数为

vX-Y，i=0.5+0.5uX-Y(i=1-n)

(5)

从n个历史样本中选取与预测年径流量的主要物理因子最相似(即联系度最大)的K个历史样本，这K个历史样本的径流量值以uX-Y所对应的相对隶属度vX-Y，i为权重进行加权平均，即得径流的预测值为

(6)

2.3 预测结果检验

选取纳什效率系数NSE和均方根标准差比RSR作为集对分析径流预测精度的评价标准[13](见表1)。具体公式为

(7)

(8)

表1 预测精度评价标准

3 结果与分析

由于人类活动对径流影响复杂，且难以量化，本文仅考虑气候因子对径流的影响，所以研究时段选取人类活动影响相对较小的时期(1963年～ 2007年)。首先本文根据互相关系数统计假设检验与集对分析检验，确定影响水资源变化的主要物理因子；在此基础上，根据影响预测径流量(1993年～2007年)的主要物理因子与历史年(1963年～1992年)的主要物理因子之间的相似性，建立径流量变化的相似预测模型，分析该流域的预测结果。

3.1 径流影响因子的确定结果与分析

由式(1)计算径流量yi与物理因子xij的互相关系数，结果见表2。在显著性水平0.05下的允许的最低相关系数值rmin=0.137；根据式(2)可知ENSO指数(MEI)xi2，海洋尼诺指数(ONI)xi3，太平洋涛动指数(PDO)xi7和降水量xi12与径流量yi之间在统计上相关显著。根据均值标准差对物理因子和径流量分别进行等级符号化处理，根据式(3)计算联系度(见表2)。

由表2知：yi与xi2间正相关趋势的比例为0.382，负相关趋势比例为0.145，不确定相关关系的比例为0.473，综合起来表现为正相关；yi与xi3间正相关趋势的比例为0.400，负相关趋势比例为0.145，不确定相关关系的比例为0.455，综合起来表现为正相关；yi与xi7间正相关趋势的比例为0.418，负相关趋势比例为0.164，不确定相关关系的比例为0.418，综合起来表现为正相关；yi与xi12间正相关趋势的比例为0.618，负相关趋势比例为0.036，不确定相关关系的比例为0.345，综合起来表现为正相关。综上所述，根据式(2)、(4)的检验要求，影响径流量yi变化的主要物理因子为ENSO指数(MEI)xi2，海洋尼诺指数(ONI)xi3，太平洋涛动指数(PDO)xi7和降水量xi12。

表2 各物理因子与年径流量的联系度和相关系数的计算

3.2 年径流预测结果与分析

为了充分利用历史数据，提高预测精度，每次仅预测1年，如预测1993年的径流量，使用1963年～1992年的历史数据；如预测1994年的径流量，使用1963年～1993年的历史数据；以此类推。

把1993年～2007年径流量主要物理因子Bn+1={zn+1，j|j=1，2，3，4}看作一个集合，1963年～1992年的径流量的主要物理因子Bi={zij|j=1，2，3，4}(i=1-30)看作另一集合，Bn+1与Bi建立集对H(Bn+1，Bi)。根据均值标准差对互相关系数统计假设检验和集对分析检验确定的主要物理因子和径流量分别进行等级符号化处理，I=0，J=-1，由式(3)得到联系度(见表3)。

因预测数据比较多，所以以1993年为例，根据最大联系度原则，从表3的30个历史样本中选出与1993年主要物理因子最相似的历史样本有2个，分别是1980年和1983年；再根据式(5)和式(6)求得1993年径流的预测值为11.653 m3/s，而实际值为13.391 m3/s，相对误差13%，满足精度要求。同理，根据上述步骤求得1994年～2007年的径流预测值。1993年～2007年径流预测值与真实值的对比结果见图1，纳什系数NES和均方根标准差比RSR见表4。

表3 年径流量的物理因子等级值和联系度计算

图1 集对分析1993年～2007年径流量的预测

表4 集对分析预测径流精度参数结果

由图1可看出，1993年～2007年实际径流量与预测径流量相接近，2004年实际值与预测值的相对误差最小，预测精度最好，而1997年和2000年实际值与预测值偏差相对较大，精度较差，原因可能是1997年是历史时期最大的水文丰水年，2000年是历史时期最小的水文枯水年，样本径流的加权平均难以达到最大最小值，致使预测值和实际值偏差较大。由表4可知，1993年～2007年径流预测NSE为0.687，RSR为0.559，整体达到“良”等级，平均误差11.4%，预测精度符合《水文情报规范》[14]要求，说明集对分析对径流的预测效果良好。

4 结 论

(1)通过互相关系数统计检验和集对分析检验的分析，影响岩溶区澄碧河流域径流量变化的主要物理因子为ENSO指数(MEI)xi2、海洋尼诺指数(ONI)xi3、太平洋涛动指数(PDO)xi7和降水量xi12。

(2)岩溶区澄碧河流域1993年～2007年径流预测的NSE为0.687，RSR为0.559，整体达到“良”等级，平均误差11.4%，表明集对分析方法在岩溶区流域中长期水资源预测中有很好的适用性，能为流域水资源调查和评价工作服务，特别适合在实测资料缺失的中小岩溶区流域。

(3)本文仅考虑气候变化对径流预测的影响，但随着人类活动加剧，势必影响岩溶区流域的径流量，需要加强这方面的研究。