基于直觉模糊层次分析法的学生认知能力综合评价

魏朝晖，骆紫燕，杜 鹃

(西安航空学院 a.能源与建筑学院；b.外国语学院；c.教务处，西安 710077)

0 引言

随着世界经济格局的变化，我国经济持续发展的内在动力是创新[1]，而人才是创新的第一资源[2]，因此，人才的培养显得就尤为重要。但是，由于每个学习个体的差异性，其认知能力也就有差别，有其擅长和不擅长的[3]。教育就是要在尊重个体的差别的基础上，实施个性化教学，为社会、经济的发展提供助力。正如法国教育学家蒙田提出教师要按学生的能力施教，这里的能力指导就是学生的认知能力。因此，对学生认知能力进行相对合理地评价，对实施个性化教学具有十分重要的意义。

近些年来，一些学者根据美国心理学教育学者布卢姆认知能力理论[4]，研究并建立了认知型学生模型。文献[5]根据布卢姆教育目标分类理论将所有知识分为识记、理解、分析、应用、综合和评价6类，然后利用作者开发的ICAI系统计算学生认知能力。文献[6]根据高中英语课程标准，利用布卢姆认知理论对2007-2012年间高考英语试卷中117份阅读理解进行分析，得出高考阅读理解主要测试学生的记忆与理解，侧重词法和句法层面的考核，而高级认知能力考查不足，思辨能力引导不够，并据此提出高考阅读理解改革建议。文献[7]根据证据中心设计理论构建一个考试的学生模型，然后根据布卢姆认知理论对高中生物的必修知识进行分类和编码，再将某编码知识内容的占比作为该编码知识的权重，汇总所有知识模块的权重得到所有知识模块的认知能力要求，以此构建了高中生物学业水平合格性考试的学生模型，并为高中生物考试提出建议。虽然基于布卢姆认知理论评价学生的认知能力取得了一些成绩，但关于认知能力定量评价的研究较少，对认知能力的权重计算不够具体，对学生测试成绩等级量化研究不够深入，满足不了个性化教学和学习的发展需求。文献[8]将布卢姆理论中的6类认知目标作为评价指标，采用偏相关系数确定各指标权重值，然后利用白化权函数确定灰色评价权值，对学生综合认知能力进行定量评价，但专家的主观性对各指标权重值影响较大，影响了评价结果的准确性。

综上所述，本文将直觉模糊层次分析法(Intuitionistic fuzzy analytic hierarchy process, IFAHP)应用于学生认知能力评价中。首先，根据修正布卢姆认知理论，从知识和认知历程两个维度建立学生认知能力评价指标体系。然后，根据学生认知能力评价指标体系制作试题测试学生，并利用三角形隶属度函数模糊化学生成绩，得到模糊评价矩阵。再聘请行业专家根据IFAHP法对学生认知能力重要性打分，获得权重矩阵。最后，对模糊评价矩阵和权重矩阵进行内积，得到学生认知能力的综合评价值。

1 布卢姆教育目标分类学

2001年，安德森等数位专家在《面向学习、教学和评价的分类学——布卢姆教育目标分类学的修订》中，将知识从知识和认知历程两个维度进行分类[9]。知识维度从内容角度明确学生学什么或教师应该教什么，认知历程维度从知识掌握程度明确学习认知过程或教师教学目标[10]。知识维度将知识分为4类：事实性知识(Factual Knowledge)、概念性知识(Conceptual Knowledge)、程序性知识(Procedural Knowledge)、元认知知识(Metacognitive Knowledge)。认知历程维度分为6类：记忆(Remember)、理解(Understand)、应用(Apply)、分析(Analyze)、评价(Evaluate)、创造(Create)。由于布卢姆教育目标分类学能很好的处理了教学目标、过程以及评价中的知识与能力关系[11]，为了综合评价学生的知识和能力，本文将知识维度的四类作为学生综合认知能力评价的一级评价指标，将认知历程维度的6类作为学生综合认知能力评价的二级评价指标。

2 综合评价的过程分析与建模

由于影响学生认知能力的因素比较多，如智力、情感、状态、激励等，而情感、状态、激励等非智力因素不易量化，造成了学生认知能力评价困难。一些学者使用模糊层次分析法[8,12]研究学生认知能力，取得了不错的效果。但是模糊层次分析法对指标权重的确定主观性过强，客观上对评价结果产生一定影响。因此，本文引入直觉模糊层次分析法(IFAHP)削弱人为主观性过强的问题[13]。

2.1 综合评价指标的构建

根据本文第一部分内容，综合知识和认知历程维度的定性定量指标建立学生认知能力评价指标集，如表1所示。在该评价指标集中，“准则层”的事实性知识、概念性知识、程序性知识和元认知知识每一个分别用“指标层”的记忆、理解、应用、分析、评价和创造。

表1 学生认知能力评价指标集

2.2 权重矩阵的确定

学生认知能力的综合评价应该是认知能力评价指标集某指标点的得分与其权重进行内积得到。不同的知识点对学生的认知能力要求不同，其权重也就不相同。而指标点的权重属于定性的变量，一般采用专家打分法。本文采用IFAHP法，聘请行业或领域内权威专家根据实际情况对学生认知能力各指标的权重进行打分，然后根据打分情况对直觉模糊判断矩阵进行一致性检验和修正，最后确定计算指标层权重。

2.2.1 直觉判断矩阵的建立

根据IFAHP法[14]，专家依据评价等级对照表(见表2)对指标层中做两两指标进行比较，得到两两指标之间直觉模糊数α=(μij,υij)。其中，μij指的是隶属度，表示i指标比j指标的重要程度；υij指的非隶属度，表示j指标比i指标的重要程度。因此可以得到直觉模糊判断矩阵R=(rij)n×n=(μij,υij)n×n,(i=1,2,…,n;j=1,2,…,n)，其表达式为

表2 评价等级对照表

其中，0≤μij≤1，0≤υij≤1，μij+υij≤1。因为专家是对两两指标互相比较，所以有μii=υjj=0.5，μij=υji，μji=υij。定义πij=1-(μij+υij)表示专家对指标i和指标j相对重要程度的不确定度或犹豫度。

2.2.2 一致性检验及修正

由于专家对指标层的打分带有一定的主观性，有可能出现指标权重不符合逻辑关系，需要对直觉模糊判断矩阵进行一致性检验[15]，具体流程如图1所示。

图1 直觉模糊判断矩阵一致性检验及修正计算流程图

首先，根据文献[16]，构造直觉模糊一致性判断矩阵

(i=1,2,…,n;j=1,2,…,n)

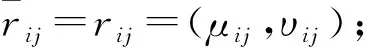
在新的直觉模糊判断矩阵R′的基础上，再进行一致性检验，直至满足一致性检验，则迭代结束，最后修正的矩阵便是满足要求的直觉模糊判断矩阵，还记作R=(rij)n×n=(μij,υij)(i=1,2,…,n)。

2.2.3 权重的确定

对于通过了一致性检验的直觉模糊判断矩阵R=(rij)n×n，采用式(7)[15]计算指标层的权重(μi,υj)n(i=1,2,…,n)。

由于式(7)还是直觉模糊矩阵，需要引入模糊转换函数[13]，然后采用式(8)计算指标层各指标的权重。

对于多位专家打分情况，由于受到专家各自知识、工作经验和学科背景的影响，各专家的打分可能有差异[16]，为了综合考虑专家打分的差异性，可根据参考文献[13]确定多专家打分时指标层的权重系数。

对于准则层的权重，由于课程大纲中规定了课程的内容，所以准则层4类知识的权重可根据大纲规定相应内容的占比确定权重。在本文中，准则层的权重用B=(bj),(i=1,2,…,m)表示(角标m表示准则层指标数目)。

2.3 评价矩阵的构建

学生的认知能力受其非智力因素影响，如身体状态、心情、情感等，其成绩具有一定程度的模糊性、不确定性。由于模糊推理具良好的鲁棒性、容错能力和自适应能力[17]，因此本文利用模糊推理对学生的测试成绩进行模糊化处理。

2.3.1 模糊评价集的建立

模糊推理的核心思想就是利用数学手段模仿人脑处理不精确、不完整信息的方式[17]。在进行模糊推理时首先要建立能将输入的信息转换为模糊语言的模糊评价集。针对百分制测试，本文将其对应五个级别的模糊评价语言，并给优、良、中、及格和不及格，如表3所示。

表3 模糊评价级别

2.3.2 模糊评价矩阵的构建

采用测试的方式测试学生认知能力时，指标层各指标点分值权重不一定相同，为了具有相同的评价尺度，需要对指标层各指标点进行归一化处理。本文采用文献[18]中的方法进行归一化处理。

由于学生的测试成绩具有一定的模糊性，需要对学生测试成绩进行模糊化处理，以提升其容错能力和自适应能力。对于经过归一化处理后的学生测试成绩，本文利用三角形隶属度函数[19]进行模糊化，并认为非智力因素影响的成绩误差为[-5,5]。如果用G=(gi)s(i=1,2,3,4,5)表示优、良、中、及格和不及格的权重矩阵，用表示测试成绩，则学生某指标认知模糊评价等级用式(9)～(13)计算，模糊三角形隶属度计算模型如图2所示。

图2 模糊三角形隶属度计算模型

学生的模糊判断评价矩阵用式(14)表示

其中：角标i表示指标，共有n个指标；角标j表示评价等级，共5级。

2.4 模糊综合评价

模糊评价矩阵W乘以直觉模糊判断矩阵G，可得到准则层下各类型知识的评价H=WG=(hm)n。

S=BH=(bm)4×(hmi)4×5=[s1,s2,s3,s4,s5] (16)

3 案例分析

布卢姆教育目标分类学从知识和认知历程两个维度定性描述了教学目标，对学习目标的描述带有一定的模糊性，只能给学习者大致的学习方向，不能说明学习目标的相对完成度情况。因此，本文以西安航空学院传热学课程为例，采用直觉模糊层次分析法定量评价学习目标相对完成情况。

3.1 构建综合评价指标

西安航空学院是一所地方应用型本科院校，主要面向地方培养应用型人才，对概念性知识和程序性知识要求较高，专业基础课传热学侧重于记忆、理解、应用、分析能力的培养。因此，本文针对西安航空学院的传热学课程，分别从准则层和指标层构建学生认知能力评价指标体系。其中，准则层包括概念性知识和程序性知识，指标层包括记忆、理解、应用和分析。

3.2 确定权重矩阵

首先，根据传热学课程大纲确定概念性知识和程序性知识的占比为，将和作为概念性知识和程序性知识的权重。然后，邀请传热学课程领域专家，参照表2(评价等级对照表)从概念性知识和程序性知识两个角度对指标层的记忆、理解、应用、分析的相对重要程度打分，结果如表4和表5所示。

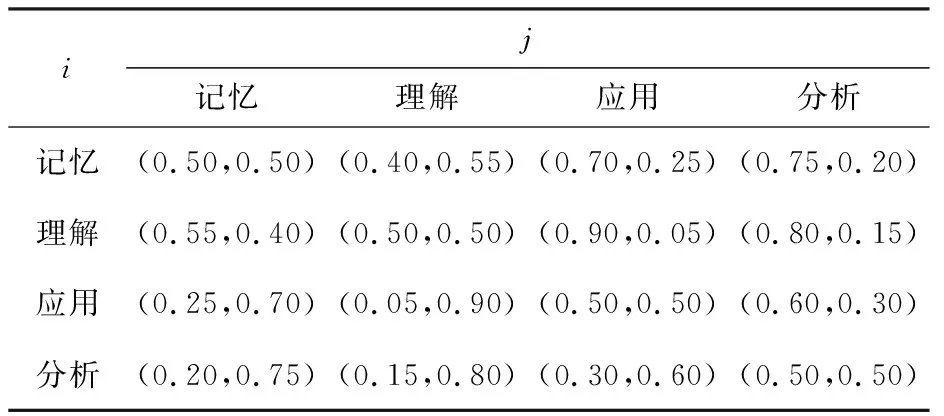
表4 概念性知识专家打分表

表5 程序性知识专家打分表

根据表4可以得出概念性知识直觉判断矩阵为

根据表5可以得出程序性知识直觉判断矩阵为

根据式(2)和式(3)，概念性知识和程序性知识的直觉模糊一致性判断矩阵分别为

将修正后的直觉判断矩阵R1和R2代入式(7)和式(8)，计算得到概念性知识各指标点权重w1=[0.3221,0.3721,0.1705,0.1353]，程序性知识w2=[0.1602,0.1856,0.3230,0.3294]。

3.3 构建评价矩阵

根据学校的人才培养定位，按照传热学课程教学大纲命制的试题，主要测试概念性知识和程序性知识学习情况。其中，概念性知识中记忆、理解、应用和分析的分值分别为15分、13分、18分和12分，总分58分；程序性知识中记忆、理解、应用和分析的分值分别为5分、13分、12分和12分，总分42分。对某班42名同学进行测试，抽取其中一名学生成绩进行分析，该生具体成绩如表6所示。

表6 班级及某同学测试成绩分配情况

由于各指标总分值不同，不能直接对各指标进行对比，需要根据该班42名同学的测试成绩，对某同学的成绩进行归一化处理，以便各指标点之间具有可对比性，同时也能体现该同学相对该班其他同学认知能力的强弱。本文采用min-max标准化法对该同学成绩进行归一化处理，处理结果如表7所示。

表7 班级及某同学测试成绩分配情况

将表7中的数据代入式(9)～(13)，可得该生认知能力模糊测试情况，如表8所示。

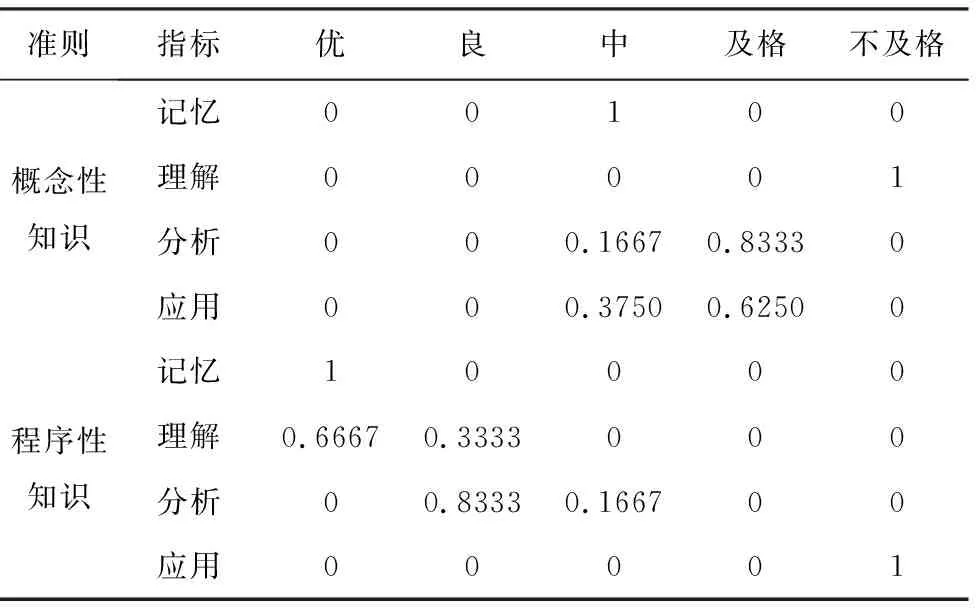
表8 某学生认知能力模糊评价表

该同学的概念性知识模糊评价矩阵如下式

该同学的程序性知识模糊评价矩阵如下式

3.4 模糊综合评价

将概念性知识各指标点权重w1和模糊评价矩阵G1代入式(15)，得到该同学概念性知识模糊评价

=[0 0 0.4102 0.2266 0.3721]

将程序性知识各指标点权重w2和模糊评价矩阵G2代入式(15)，得到该同学程序性知识模糊评价

=[0.2858 0.3310 0.0538 0 0.3294]

H1与H2组成准则层模糊评价矩阵H=[H1,H2]T。将准则层权重B=[0.58,0.42]T准则层评价模糊矩阵H=[H1,H2]T代入式(16)，可得该生综合模糊评价值S=BH

=[0.1200 0.1390 0.2553 0.1314 0.3542]

从该同学概念性知识模糊评价H1可以看出，该生优、良、中、及格、不及格占比分别为0%、0%、41.02%、22.66%、37.21%。从该同学程序性知识模糊评价H2可以看出，该生优、良、中、及格、不及格占比分别为25.58%、33.1%、5.38%、0%、32.92%。说明该生相对其他同学，在概念性知识方面表现较差，优和良成分皆为0%；在程序性知识方面，虽然优和良成分占了一半的成分，但仍有32.92%的不及格成分，仍有薄弱点。

该生综合模糊评价优、良、中、及格、不及格占比分别为12%、13.9%、25.53%、13.14%、35.42%，不及格占比超过35%。基于知识相对重要性考虑，该生有超过35%的知识认知不达标。结合表8可以看出该生认知能力特点。该生擅长程序性知识学习，特别是程序知识中的记忆和理解能力较强，而弱于概念性知识学习，尤其是概念性知识中理解能力非常薄弱。究其原因，该生虽然记住了概念性知识大部分知识点，但未能理解，影响到了记忆能力，进而影响到了分析和应用能力；该生虽擅长程序性知识的记忆与理解，但不能融会贯通，影响了应用能力。

基于上面分析，该生在以后概念性知识学习中，重点应该放在理解能力的提升上，特别是知识细节的理解，多接触工程案例，提升分析和应用能力。在以后程序性知识学习中，重点放在知识的运用上，多做练习，多应用知识。

4 结论

学生认知能力易受非智力因素影响，且不易量化。因此，本文以布卢姆理论为基础，采用层次分析法构建学生认知能力评价体系，然后使用直觉模糊法计算各指标权重，使用三角形隶属度函数模糊化学生测验成绩，将指标权重与模糊化后的测验成绩取内积，得到学生模糊综合认知能力评价，最后结合具体案例，验证了该方法的有效性，并根据案例计算结果分析了某学生认知能力，对其以后学习提出建议，说明该方法具有一定的实用价值。