基于循环神经网络和卡尔曼滤波器的多变量混沌时间序列预测

胡 艳

(广西财经学院防城港学院 广西 南宁 530003)

0 引 言

在许多工程应用领域中均存在时间序列类型的数据，对时间序列的挖掘处理必须考虑数据间的时间关系，从复杂的海量时间序列中挖掘有价值的知识，具有重要的意义[1-2]。混沌时间序列是一种由非线性动力系统所产生的复杂行为，是一种普遍存在的不规则运动，典型的混沌时间序列包括煤矿瓦斯浓度[3]、航站楼离港旅客流量[4]和数控机床热误差时间序列[5]等。许多研究表明混沌时间序列具备短期内的可预测性[6-7]，因此混沌时间序列的预测成为当前的一个热门研究领域。在多变量的混沌时间序列问题中，容易出现多重共线性的现象，多变量之间由于存在高度相关性，导致预测模型的泛化能力有限，预测性能降低，容易陷入局部极小，且收敛速度慢[8]。

利用统计机器学习和深度学习技术对时间序列进行在线预测是当前最为常见的一类方法，而向机器学习或神经网络加入多重非线性的处理机制存在一定的困难。文献[9]为极限学习机的权重调节矩阵引入惩罚因子，通过惩罚因子降低高相关性变量的权重，从而缓解了多重共线性的效应。文献[10]为神经网络的输出权重设计了平滑处理机制，通过正则项缓解混沌时间序列的多重共线性效应。现有的多重共线性解决机制大多通过增加一个独立的检测和调节模块，而这些模块一般也通过若干次的迭代学习搜索最佳的输出权重矩阵，导致计算负担较重。

多变量混沌时间序列预测算法为了保证较低的模型复杂性，大多采用单层神经网络结构。混沌时间序列的鞍点数量远多于局部最优点数量，许多研究表明，深度学习技术对这种问题的效果明显好于单层神经网络。本文运用可扩展性较好的循环神经网络(Recurrent Neural Network,RNN)作为序列学习机，使用实时递归学习算法搜索最小化预测误差的最优网络参数，采用Levenberg-Marquardt算法对神经网络进行迭代训练。将序列的学习问题映射到动态线性模型是解决多重共线性问题的一个有效手段，本文利用卡尔曼滤波器对网络的输出权重进行调节，缓解隐层输出矩阵的多重共线性问题。此外，将卡尔曼滤波器和神经网络集成，能够减少奇异矩阵的运算量，加快网络的训练速度。

1 基于循环神经网络的序列学习

1.1 深度循环神经网络(DRNN)

DRNN由栈式网络层构成，使用实时递归学习算法(Real Time Recurrent Learning,RTRL)进行非线性训练。本文DRNN序列学习机结构如图1所示。

图1 基于DRNN的时间序列预测流程

Yn(k)=fANN(Yn(k-1),Yn(k-2),…,Yn(k-q),

U(k-1),U(k-2),…,U(k-p),Φ)

(1)

式中：函数fANN表示输入信号和输出信号之间的非线性关系。

将循环网络关于时间展开，则变为深度前馈神经网络。图2所示为RNN关于时间展开的结构示意图。图中每个圆形为一个网络层，可能是输入层、隐层和输出层。单隐层RNN的展开结构如图2(a)所示，该RNN网络以一定的步长采集当前的输入信号，单隐层的RNN结构仅能处理时间t的输入数据，而多隐层的结构可以采集当前时间t输入数据不同深度的数据空间，本文的多层RNN在时间域和空间域均达到了较高的深度。

(a) 单层循环神经网络

1.2 训练DRNN

DRNN结构的训练程序包括计算误差和计算梯度两个步骤。

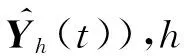
U(k)↔U(k-1)↔…↔U(k-p)]

(2)

式中：“↔”表示序列连接操作。隐层(s=1,2,…,n-1)和输出层(s=n)的输出向量分别定义为：

nets(k)=[net1,net2,…,netNs]+Bs

(3)

式中：s=1,…,n-1,n;⊙表示矩阵元素间的乘法。

(4)

训练DRNN等价于调节DRNN网络参数Φ的过程，训练过程中DRNN的输出序列逐渐接近真实的序列。网络的训练目标定义为：

(5)

(6)

(7)

2) 计算梯度。使用RTRL算法[11]训练DRNN。以4层神经网络为例介绍本文梯度学习的过程，其包括1个输入层、2个隐层和1个输出层。输出层误差ei(k)关于W3,2的偏导数计算为：

(8)

(9)

式中：zim=(i-1)q+m；σ表示克罗内克函数。如果n3=d或n2=l，则σ(n3,d)(n2,l)=1；否则σ(n3,d)(n2,l)=0。

隐层误差ei(k)关于W2,1的偏导数计算为：

(10)

(11)

(12)

(13)

输入层误差关于权重W1,0的偏导数计算为：

(14)

(15)

(16)

(17)

采用基于梯度的Levenberg-Marquardt方法[12]训练DRNN模型。

2 卡尔曼滤波器调节隐层输出

2.1 卡尔曼滤波器

使用卡尔曼滤波器调节隐层的输出权重，利用卡尔曼滤波器处理多重共线性问题。考虑一个动态系统，其状态向量定义为能够唯一描述系统动态行为的最小数据集，记为xk，k表示离散序列的时间点。一个动态系统可定义为以下的方程组形式：

xk+1=Ak+1|kxk+wk

(18)

yk=Hkxk+vk

(19)

式中：xk为状态向量；yk为观察序列的向量；Ak+1|k为状态xk从时间k到时间k+1的转移矩阵。yk为时间点k的观察样本，Hk为度量矩阵。式(18)和式(19)分别为系统的状态方程和度量方程。噪声表示为：

(20)

式中：wk表示加性高斯白噪声，噪声的均值为0；Qk为协方差矩阵。

卡尔曼滤波器是一种回归型估计器，算法1是估计状态的卡尔曼滤波器递归程序。

算法1估计状态的卡尔曼滤波器递归算法

2.P0=E[(x0-E[x0])(x0-E[x0])T]

3. whilek≠n

//传播状态的估计

//传播协方差的误差

//计算卡尔曼增益矩阵

//更新状态的估计

//更新协方差的误差

9. endwhile

在动态系统中，式(18)-式(20)的矩阵Hk、Ak、Rk(测量噪声的协方差矩阵)、Qk是已知的，而在时间序列的学习问题中，这些参数的历史数据是已知的，本文假设时间序列模型的矩阵依赖一个未知的向量参数，记为ψ。ψ的经典求解方案是最大似然估计，但这种方案增加了卡尔曼滤波器的矩阵求逆运算数量和矩阵乘法运算数量，所以导致序列学习算法的计算成本大幅度升高。

本文采用低计算复杂度的噪声自协方差估计算法[13]估计未知参数ψ，该方法将状态方程映射为一个线性时不变模型，其解是离散矩阵Ak和Qk，两个矩阵分别定义为：

Ak=exp(FΔtk)

(21)

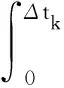
(22)

式中：F、L、Qc为常量矩阵，描述了模型的行为；Δtk=tk+1-tk为离散变换尺度的增量。F为反馈矩阵，其值定义了状态估计的传播速率，如果F值接近0，其状态估计类似于传统的线性回归过程，如果F值较大，其状态估计的变化速度较快；L为噪声效应矩阵，一般设为单位矩阵；Qc为指定对角元素的密度矩阵，对角以外元素的缺省值为0。

一些情况下通过式(22)无法计算出协方差矩阵Qk，此时通过以下的分数分解处理：

(23)

然后，协方差矩阵Qk可计算为：

(24)

该方法无需通过迭代程序来估计矩阵Ak和Qk，所以其计算复杂度明显低于最大似然估计方法。

2.2 非线性卡尔曼滤波器

对卡尔曼滤波器进行扩展，使其满足非线性系统优化滤波器的条件。使用高斯近似联合分布处理系统的状态和度量，基于泰勒序列进行线性变换：

x～N(m,P)y=g(x)

(25)

式中：x∈Rn,y∈Rm,g:∈Rn→Rm为非线性函数；m为估计的状态均值，P为状态的协方差。变量x和y的线性近似值定义为：

(26)

(27)

基于卡尔曼滤波器更新循环神经网络隐层的输出权重。初始化阶段使用式(21)和式(24)估计转移矩阵A和协方差矩阵Qk，通过度量训练时间序列的协方差计算出矩阵Rk。然后对于每一批新到达的时间序列，通过卡尔曼滤波器更新网络的输出权重。在序列学习过程中矩阵A、Qk和Rk为常量，仅仅更新回归系统的参数。最终，使用卡尔曼滤波器输出的回归系数调节网络的输出权重矩阵。

3 实 验

仿真实验在Intel Core i5-8265 CPU,主频1.80 GHz,8 GB内存，MATLAB R2011b编程环境下完成。

3.1 实验数据集

为证明提出模型的有效性，选择7个公开的多变量混沌时间序列数据集作为基准数据集，分别为Abalone、Auto MPG、Blog、Communities、Cycle、Energy和Housing数据集[14]。表1所示是基准数据集的数据量和属性数量，将每个数据集按60%、10%和30%的比例分别划分为训练集、验证集和测试集。

表1 实验的基准数据集

3.2 实验方法

实验中时间序列的每批长度选定为5个观察信号，采用1.2节的训练方法训练每个数据集。通过预处理实验训练每个数据集的最优网络参数，每个数据集的最优结构参数如表2所示。

表2 每个实验数据集的DRNN结构

每数据集的实验采用表2所示的DRNN网络结构，隐层采用log-sigmoid激活函数f(γ)=1/(1+e-γ)，输入层和输出层采用线性激活函数。在线学习序列的过程中，仅通过卡尔曼滤波器实时计算递归位置参数，并根据该参数调节DRNN隐层的输出权重矩阵。

每组实验独立地运行30次，统计30次的平均值和标准偏差作为最终的性能结果。

选择5个考虑多重共线性问题的时间序列预测算法与本文算法比较，横向验证本文算法的有效性。对比方法如下：

(1) CVEA[15]：采用交叉验证解决自回归模型的多重共线性问题。

(2) DTS[16]：通过矩阵分解处理网络的输出权重矩阵，再通过距离度量评价分解元素之间共线性严重程度。

(3) ROTSP[17]：一种基于单层循环神经网络的时间序列预测算法，并未包含多重共线性问题的处理机制。

(4) LSTM[18]：一种基于长短期记忆的循环神经网络模型，其有效地提高了循环神经网络的学习效率。

(5) AWNN[19]：一种基于小波神经网络的时间序列预测模型，通过小波函数实现了非线性预测能力，并且接近单层神经网络的效率。

3.3 预测准确率实验

采用根均方根误差(Root Mean Square Error,RMSE)作为预测性能的评价指标，定义如下：

(28)

图3所示为6个时间序列预测算法对于7个测试数据集的预测误差结果，本文算法对于Abalone、Auto MPG、Communities、Cycle、Energy和Housing数据集的预测误差均低于其他对比方法。综合比较图中的结果，可看出深度神经网络的预测性能好于单层神经网络。DTS算法虽然考虑了多重共线性问题，但是单层神经网络也严重限制了总体的预测性能。

图3 时间序列的预测误差实验

3.4 多重共线性实验和结果分析

多重共线性的出现情况一般为两个以上的预测器之间高度相关，这种情况下，模型包含的预测器越多，则预测的准确率越低。本文首先评估原数据集属性之间的线性依赖程度，采用方差膨胀系数(Variance inflation factor, VIF)和条件指数(Condition Index, CI)评估每个属性的多重共线性的严重程度。第k个属性的VIF定义为：

(29)

CI定义为：

(30)

式中：λ1为矩阵的最大特征值；λl为第l大的特征值。如果CI值在0～10范围表示属性之间是弱依赖性；如果CI值在10～30范围表示属性之间是普通依赖性；如果CI值在30～100范围表示属性之间是高度依赖性；如果CI值大于100表示属性之间是强依赖性。

表3所示为原数据集的最大VIF值和最大CI值。经多次测算，Blog数据集的最大VIF值很大，且无确切数值。可以看出，Cycle数据集和Housing数据集的属性之间依赖性较低，Abalone数据集和Auto MPG数据集的属性之间依赖性中等，而Blog数据集、Communities数据集和Energy数据集的属性之间依赖性很高。

表3 数据集特征的多重共线性分析

在神经网络模型中，经过隐层映射之后的输出矩阵列之间一般具有高度的相互依赖性，但如果依赖性过高，则会出现多重共线性问题，导致预测的性能受到严重影响。本文网络模型对每个数据集分别独立地训练50次，统计了其中最大的CI值和VIF值以及平均CI值和VIF值，结果如表4所示。结果显示，原数据集中相关性过低的数据集经过本文网络模型的学习，相关性得到提高，符合神经网络的特点；而原数据集中相关性过高的数据集经过本文网络模型的学习，有效地降低相关性，体现了卡尔曼滤波器的权重调节效果。

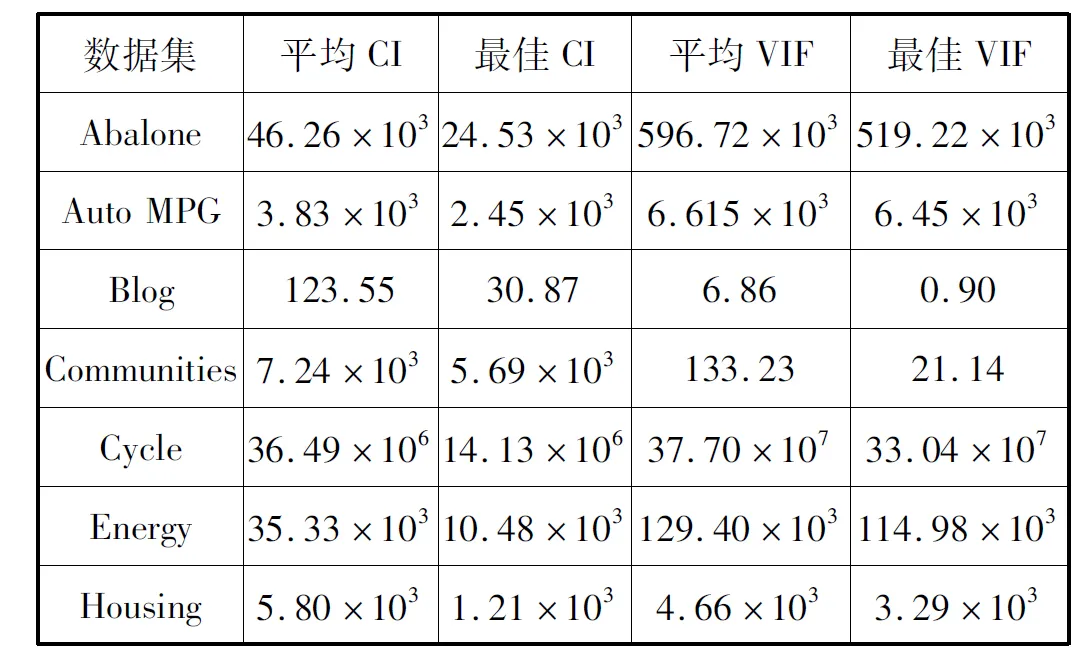
表4 数据集特征的多重共线性分析平均值(RBF激活函数)

3.5 训练时间对比

对比本文DRNN模型与LSTM模型、AWNN模型的训练时间。将LSTM网络的隐层数量设为和本文DRNN一致，将隐层深度记为L，每个数据集的L值设为参数优化程序的平均值。

统计平均训练100个观察时间序列数据的平均时间，结果如表5所示。可以看出，AWNN的小波函数对于混沌时间序列的计算量依然很高，其训练时间高于DRNN。而LSTM在训练高维混沌时间序列的过程中，包含大量的矩阵求逆运算，导致其训练时间较长，而本文方法的激活函数较为简洁，且卡尔曼滤波器避免了大部分的矩阵求逆运算，仅保留了非奇异矩阵的求逆运算，因此达到了较好的训练效率。

表5 不同网络模型的平均训练时间 s

4 结 语

本文利用具备时间域和空间域可扩展能力的循环神经网络作为序列学习机，使用实时递归学习算法搜索最小化预测误差的最优网络参数，采用Levenberg-Marquardt算法对神经网络进行迭代训练。利用卡尔曼滤波器对网络的输出权重进行调节，缓解隐层输出矩阵的多重共线性问题。此外，将卡尔曼滤波器和神经网络集成，能够减少矩阵的运算量，加快网络的训练速度。实验表明，本文算法有效地缓解了多变量混沌时间序列的多重共线性问题，并且对时间序列实现了较好的预测性能，其时间效率也高于传统的深度神经网络。

本文DRNN的网络结构参数选定过程依然较为繁琐，目前预处理的训练程序较为耗时。未来的研究重点是设计一套深度循环神经网络的结构参数优化程序，通过少量训练集选定最优的网络结构参数。