Impacts of sampling design on the abundance estimation of Portunus trituberculatus using crab pots*
Chunyang SUN, Yingbin WANG
School of Fisheries, Zhejiang Ocean University, Zhoushan 316022, China
Abstract Fishery-independent surveys can provide high-quality data and support fishery assessment and management. Optimization of sampling design is crucial to increase the quality of fishery surveys.Crab pots are important fishing gears used to catch crabs. We analyzed the impacts of sampling design of crab pots on the abundance of Portunus trituberculatus in the Changjiang (Yangtze) River estuary to the Hangzhou Bay and its adjacent waters in East China Sea. The crab pots were cylindrical, 240 mm in height and 600 mm in diameter of the iron ring. Our sampling designs (including fixed-station sampling, simple random sampling, stratified fixed-station sampling, and stratified random sampling), three number of stations(9, 16, and 24), and three numbers of crab pots (500, 1 000, and 3 000) were simulated and compared with the “true” abundance that obtained from bottom trawl surveys in the study area in 2007. The scenarios with 16 stations were set in stratification as a control group for comparison with unstratified designs. Results show that simple random sampling can obtain more stable results than fixed-station sampling in the abundance estimation of P. trituberculatus. In addition, stratified sampling resulted in more accurate abundance than unstratified sampling. The accuracy of the simulated results improved with the increase of the number of stations. No remarkable differences in the results were found among the scenarios of diff erent number of crab pots at each station. However, resource-intensive areas exerted great impacts on simulation results. Thus,prior information or pre-survey results about resource abundance and density distribution are necessary. This study may serve as a reference for future sampling designs of crab pots of P. trituberculatus and other species.
Key word: sampling design; number of sampling station; sampling time; Portunus trituberculatus;abundance estimation; crab pot
1 INTRODUCTION
Fishery survey data are the basis of stock assessment and management (Jardim and Ribeiro,2007). The design of sampling schemes has received increasing attention because of the demand for highquality data of fishery resources (Chen, 1996; Cao et al., 2014). However, limited funds, time, and complex marine geological conditions are frequently encountered problems in resource surveys (Barbraud et al., 2012; Dorner et al., 2013; Cao et al., 2014).Simulations using computers for sampling design can eff ectively avoid the above problems because they can save cost while ensuring the complete use of data,maximize the investigation benefit (Simmonds and Fryer, 1996; Liu et al., 2009), and give the optimal option by comparing diff erent sampling designs.
Scientific survey design can provide information about the target population, such as resource abundance and distribution at a certain spatialtemporal scale (Jardim and Ribeiro, 2007). In 2017,the Ministry of Agriculture selected Zhejiang North Fishing Ground as a pilot area to carry out the catch quota management (CQM) of Portunus trituberculatus(Anonymous, 2018). CQM is currently an advanced measure in fishery management. Based on the scientific monitoring and assessment of fishery resources, a total allowable catch (TAC) of target species over a certain period is determined and assigned (Huang and Huang, 2002). Thus, survey data are the basic factor for determining the appropriate TAC.
Portunus trituberculatus is an important coastal economy species in China (Song et al., 2006). The total catch of P. trituberculatus in China exceeded 500 thousand tons in 2016 (Editorial Committee of China Fishery Statistical Yearbook, 2017). Zhejiang is the province with the highest yield of P. trituberculatus, which accounts for about 35% of the total catch in China of this species (Editorial Committee of China Fishery Statistical Yearbook,2019). The catch of P. trituberculatus in Zhejiang Province increased about 30% during the past 10 years(Sun, 2018). The annual TAC of P. trituberculatus in the pilot area was determined by resource survey.Therefore, a scientific and reasonable sampling plan for crab pots is crucial.
Fixed-station sampling is often used in China’s fishery resource survey. By investigating resources at fixed stations, this method can compare the dynamic changes of resources in diff erent years (Zhao et al.,2014; Wang et al., 2018). Simple random sampling is the basis of other sampling method and is often used as the standard to compare with other sampling methods (Jin et al., 2008; Liu, 2012). Stratified random sampling is supported by the theory of classical statistics (Cochran, 1977; Manly et al., 2002;Miller et al., 2007), which is widely used in the scientific investigation of fishery resources because it can make selected samples more representative and improve the estimation accuracy of parameters (Smith and Gavaris, 1993; Gou, 2005; Xu et al., 2015).
Crab pots are passive fishing gears with the advantages of simple structure, low cost, convenient operation, high catch, and less damage to the ecological environment (Lin et al., 2013; Zhang et al.,2015). Therefore, crab pots are used worldwide and are very popular in Europe, America, Australia, New Zealand, South Korea, Japan, and other countries(Watanabe and Yamasaki, 1999; Stevens et al., 2000).For example, almost all commercial crab fishermen in Louisiana and the Gulf Coast of Mexico use crab pots(Yang, 1999). Crab pot fishery in the East China Sea began in 1980-1990 and was introduced from South Korea and Taiwan of China to Zhejiang, Jiangsu, and Fujian Provinces. The crab pot fishery flourished in the early 1990s, and has now become an important form of fishery in the East China Sea (Zhang et al.,2010b).
Despite the above advantages, the shortcomings of using crab pots in survey methods are obvious. The soak time of pots can produce biased simulation results for the catch of Dungeness crabs (Miller, 1979;Smith and Jamieson, 1989). The difference among seasons can also aff ect the estimation of crab abundance (Bennett, 1974). Previous studies lacked the research on the algorithm of crab pots capturing P. trituberculatus.
In the current study, we conducted a pre-experiment on soaking time. Then, we assessed four sampling designs (including fixed-station sampling (FS),simple random sampling (SR), stratified fixed-station sampling (SFS), and stratified random sampling(SRS) designs) in the Changjiang (Yangtze) River estuary to the Hangzhou Bay and its adjacent waters of East China Sea for four seasons using an independent algorithm that we established for the simulation of P. trituberculatus capture. The goals were to establish an algorithm to calculate the probability that each P. trituberculatus could be caught in the sampling area to estimate the abundance of P. trituberculatus in the study area; to compare the performances of diff erent sampling designs (fixedstation sampling and simple random sampling,stratified sampling and unstratified sampling) in the study area; to compare the eff ectiveness of diff erent numbers of stations when estimating the abundance of P. trituberculatus; and to compare the impact of diff erent numbers of crab pots on sampling results.
2 MATERIAL AND METHOD
2.1 Study area and data collection period
The study area was the Changjiang River estuary to the Hangzhou Bay and adjacent area (29°N-32°N,120°E-125°E), which is the pilot water of the CQM of P. trituberculatus (Fig.1). The water depth of the study area was between 20 and 50 m (Su, 2005).Fishery resources are abundant in this area, which is a traditional fishing ground in Zhejiang, Jiangsu,Fujian, Shanghai, and Taiwan, China (Ding et al.,1987; Zheng et al., 2003).
The distribution and density data of P. trituberculatu were collected quarterly (February, May, August, and November) in 2007 from 34 sampling stations, which were identified through fixed-station sampling (Fig.1).A single otter trawl vessel with main engine power of 50 kw was used to conduct the bottom trawl surveys.The towing speed was 2 knots and hauled 1 h at each sampling station. The eff ective open width of the sampling net was 15 m.

Fig.1 Study area and original sampling stations in 2007
2.2 Dynamic distribution base map of Portunus trituberculatus
The “true” abundance of P. trituberculatus was estimated using the sweep area method based on the data collected from 34 stations in the study area in the four seasons in 2007 (Han et al., 2019). Then, the survey area was divided into 850 sampling grids of about 6′×6′, and the Kriging interpolation method was used to interpolate the unknown elements in the whole study area (Cressie, 1993; Rivoirard et al.,2008; Liu, 2012). The abundance of P. trituberculatus varied greatly among in season and in region for breeding, feeding, and overwintering (Wu et al.,2016). The base maps of resource distribution of the four seasons were produced and then used as the base of the sampling design for the next work (Petitgas,2010; Pokhrel et al., 2013) (Fig.2). P. trituberculatus individuals were allowed to move in the actual situation rather than fixed to allow predation, avoid predators, and adapt to the external environment(salinity, current, temperature, etc.) (Cheng et al.,2012; Ding et al., 2014; Sun, 2018). In addition, each sampling scenario was repeated 1 000 times. The fixed resource distribution base map not only interrupts the actual situation but also makes repeated simulation work meaningless. The principle of the individual distribution on the base map was that the P. trituberculatus abundance within each sampling unit was known. The corresponding coordinate values were randomly generated inside the unit area when the unit was selected, representing each location of P. trituberculatus. New coordinates were randomly generated in each sampling unit and each sampling scenario was repeated 1 000 times by computers.
2.3 Specification and placement of crab pots
The fishing gear and fishing method of crab pots were determined according to the investigation in Daishan County of Zhejiang Province (Lin et al.,2013). The crab pots were cylindrical with 240 mm height, and the diameter of the iron ring was about 600 mm. All crab pots had the same specifications. As a passive fishing gear (Tang and Wu, 1990; Zhang et al., 2010a), the crab pot has an upper limit of catching capacity. No relevant literature and independent experiments were available about the maximum catch of crab pots as support. Therefore, experts and fishermen were consulted, and 10 was considered as the maximum number of catch for each pot (personal communication).
In our simulation work, the crab pots were placed in the north-south direction (Lin et al., 2013). The fishing boat travelled at a constant speed (8-10 kn) in a constant direction, and a group of crab pots was placed in the water in turn (Lin et al., 2013). In total,500, 1 000, and 3 000 crab pots were selected in the simulation work. Then, 500 and 1 000 crab pots were connected to one main rope. The interval between two crab pots was 8 m. Furthermore, 3 000 crab pots were divided into three parallel lines with 1 000 crab pots on each line, and an interval of 0.2 n mile was assumed between two strings.
Crabs approach the pots along the odor field gradient of the bait, and the bait in the pot plays an important role in the induction (Chapman and Smith,1978). The trapping eff ect of bait is also the biological basis of the algorithm established in our research. In our simulation work, the dates when the pots were placed into the sea were consistent with the actual sampling work for the four seasons, which was performed at the beginning of February, May, August,and November.
The soaking time of crab pot in the sea has a great impact on the quantity of capture (Hong et al., 1999).Three time options (6, 10, and 16 h) with nine sampling stations and 1 000 crab pots were set for simulation analyses to determine the appropriate soaking time (Lin et al., 2013; Zhang et al., 2015).The optimal soaking time was chosen and then used in each simulation scenario.
2.4 Sampling design
Four sampling designs, including FS, SR, SFS, and SRS, were selected for the simulation study. Three numbers of station (9, 16, and 24) were set to evaluate the influence of station number on the estimated results (Fig.3).
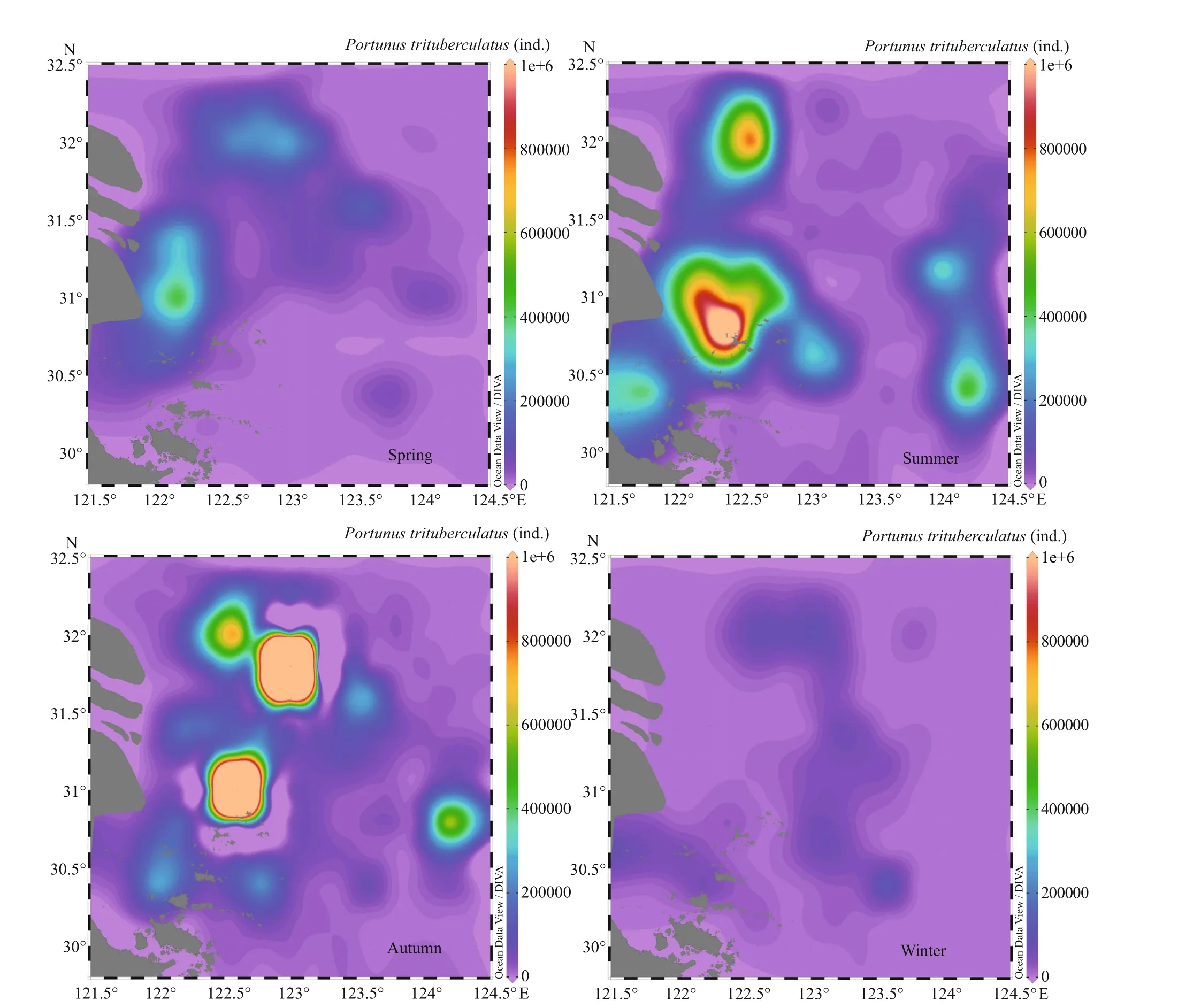
Fig.2 Base map of dynamic distribution of P. trituberculatus resources in each season
1) FS (fixed-station sampling): 9, 16, and 24 stations out of the 850 potential sampling stations were selected (Li et al., 2015). One sampling station was set in the estuary to ensure the sampling can better represent the study area because of the special environment of hydrology and ecological characteristics in this area.
2) SR (simple random sampling): 9, 16, and 24 stations were randomly selected from all 850 potential stations without replacement in each simulation.
3) SFS (stratified fixed-station sampling): Based on the resource distribution and isobaths, three strata(A, B, and C) were divided and the number of sampling stations in each stratum was allocated according to the stratum’s area and the variance of density of resource in each stratum. The scenario of 16 stations was selected as a control group of stratified sampling, and 10, 4, and 2 sampling stations were chosen for strata A, B, and C, respectively.
4) SRS (stratified random sampling): the situation of 16 stations was conducted, and the locations of sampling station (10, 4, and 2) in each stratum (A, B, and C) were selected randomly without replacement.
Three numbers of crab pots (500, 1 000, and 3 000)were assumed to put in each station to evaluate the impact of the number of crab pots on the estimated results.
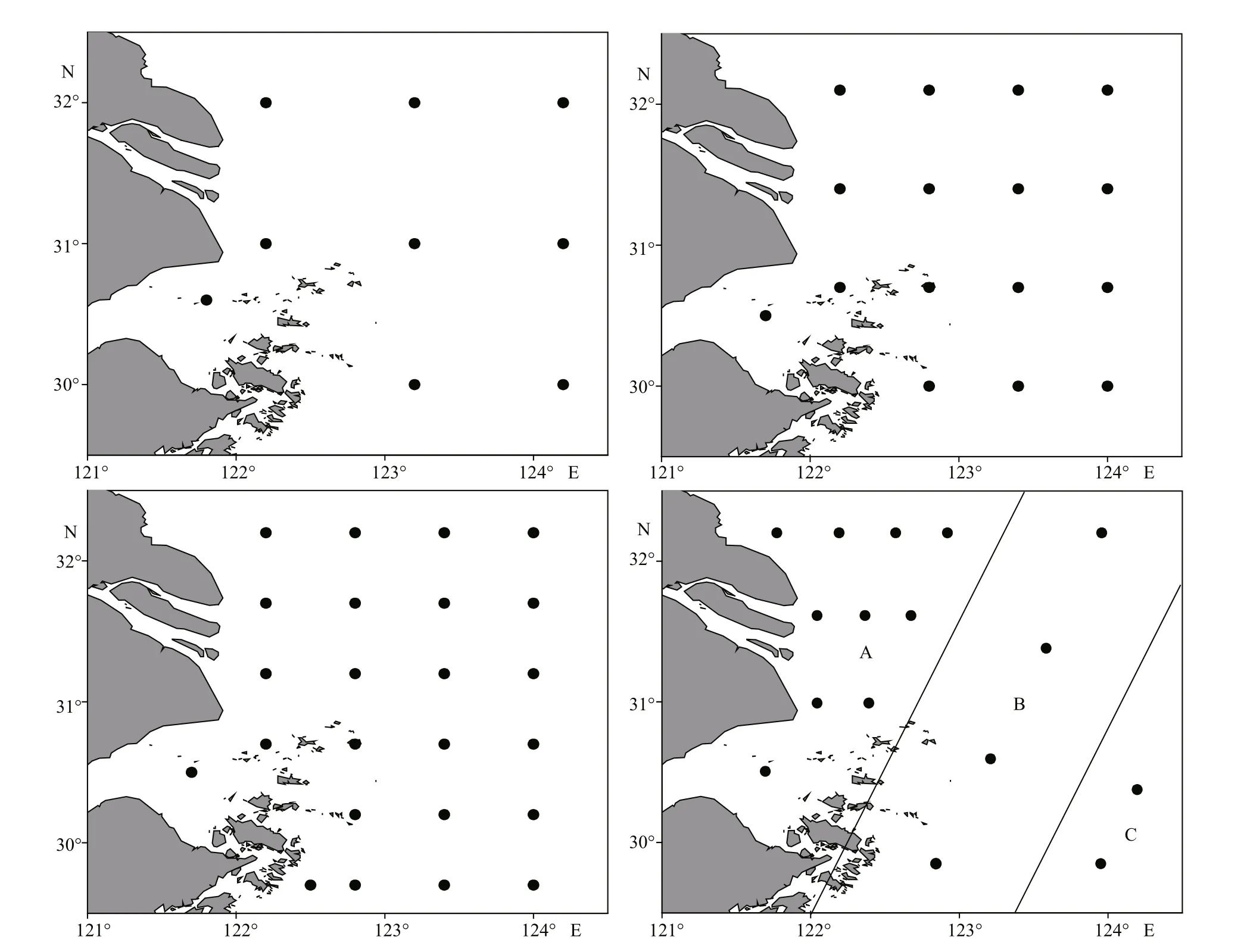
Fig.3 Layout of 9, 16, and 24 stations in fixed-station sampling and 16 stations in stratified fixed-station sampling (strata A, B, C)
2.5 Algorithm and performance indices
An algorithm calculating the capture probability of crab pots and the number of P. trituberculatus that can be caught by the crab pots was built. The schematic diagram of the crab pot catching P. trituberculatus shows the principle of fishing (Fig.4). The formula(Eq.1) is as follows:
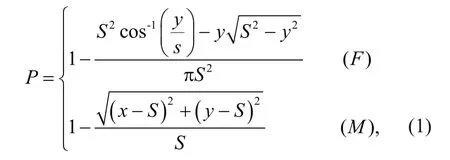
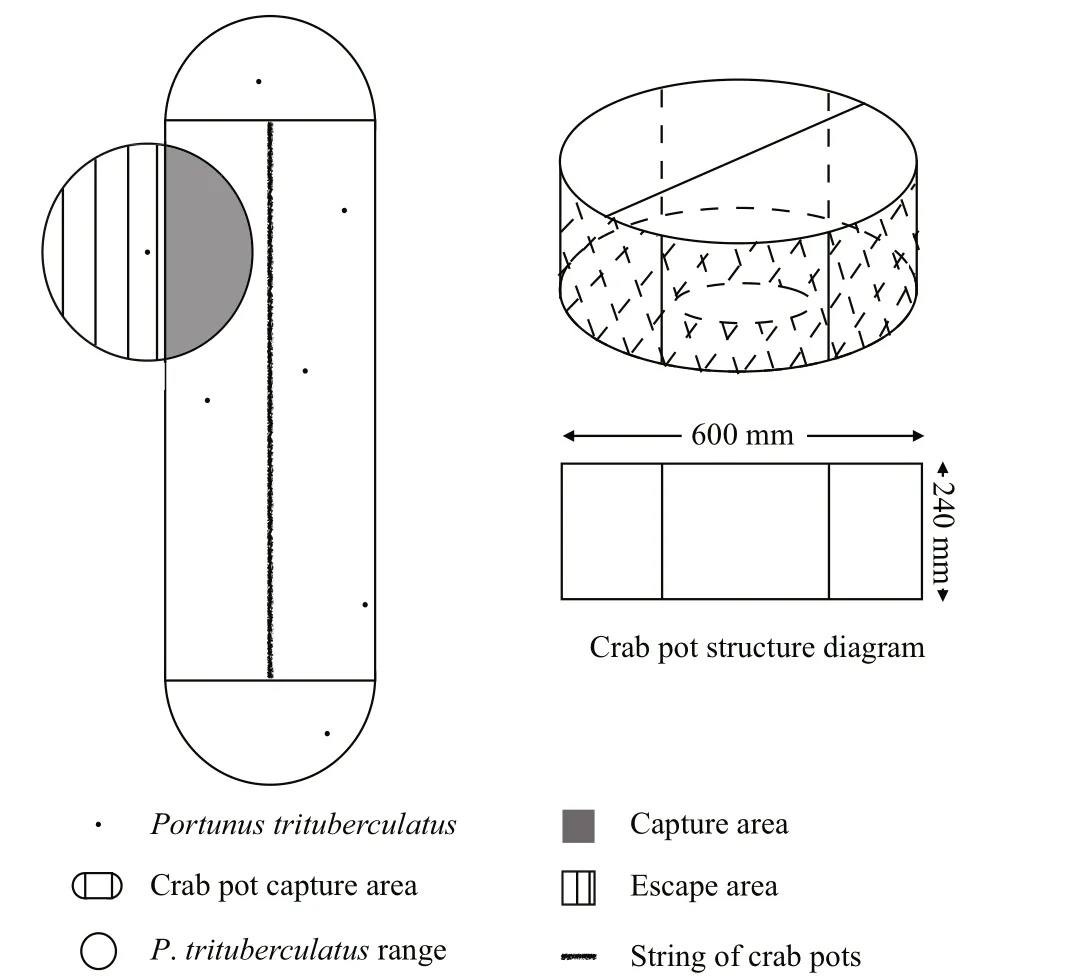
Fig.4 Schematic diagram of the crab pot catching P. trituberculatus
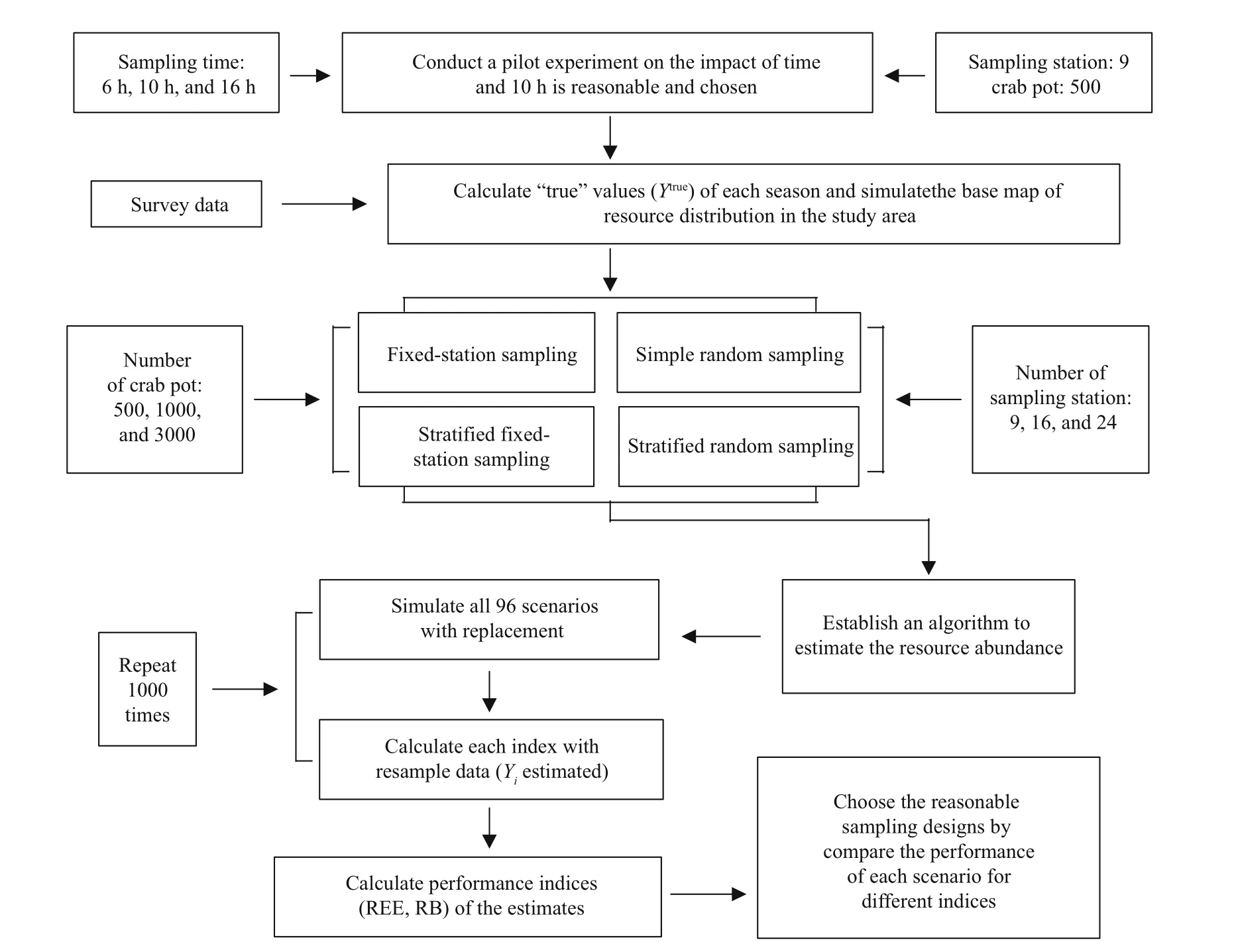
Fig.5 Flowchart of the simulation study summarizing the simulation framework for the reasonable sampling station designs for fishery-independent survey using crab pot
where P is the probability that each P. trituberculatus could be caught; S is the furthest distance that P. trituberculatus can move during the crab pot sampling time; x and y represent the position of each P. trituberculatus that can be caught within the range of the crab pots. The crab pot capture area was divided into one rectangular area and two semicircular areas(Fig.4). When the individual’s location is in the rectangular area, equation ( F) should be selected;when the individual’s location is in the semicircular areas, then equation ( M) should be selected. In a simulated sampling process, all the calculated P values were added to obtain the nominal probability of P. trituberculatus that can be caught by this sampling design.
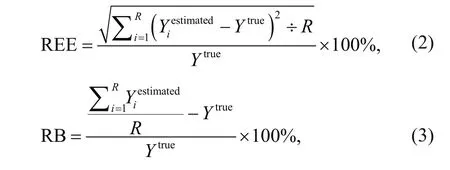
The relative estimation error (REE) and relative bias(RB) were calculated to evaluate the results of abundance for diff erent sampling scenarios (Eqs.2 & 3).
2.6 Simulation procedure
A simulation framework for sampling design was developed (Fig.5). Four sampling designs (FS, SR,SFS, and SRS) with three numbers of sampling stations (9, 16, and 24) and crab pots (500, 1 000, and 3 000) composed 96 scenarios (Table 1). The sampling area of the crab pots is located inside the sampling unit of the dynamic resource distribution base map.Individuals of P. trituberculatus in the crab pots sampling area were selected, and the probability that each P. trituberculatus could be captured was calculated using the established algorithm. The sum of the values was considered the amount of P. trituberculatus resources that this sampling scheme could capture. Then, the sweep area method was used to simulate the abundance of P. trituberculatus in the study area. Each sampling scenario was repeated 1000 times. The performance indices (REE, RB) were calculated to compare the simulation eff ect of diff erent sampling scenarios and then choose the reasonably sampling designs.
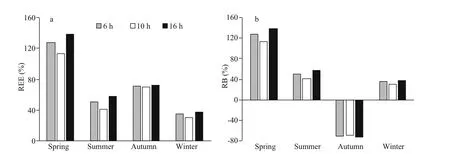
Fig.6 Relative estimation error (REE) and relative bias (RB) of diff erent sampling times
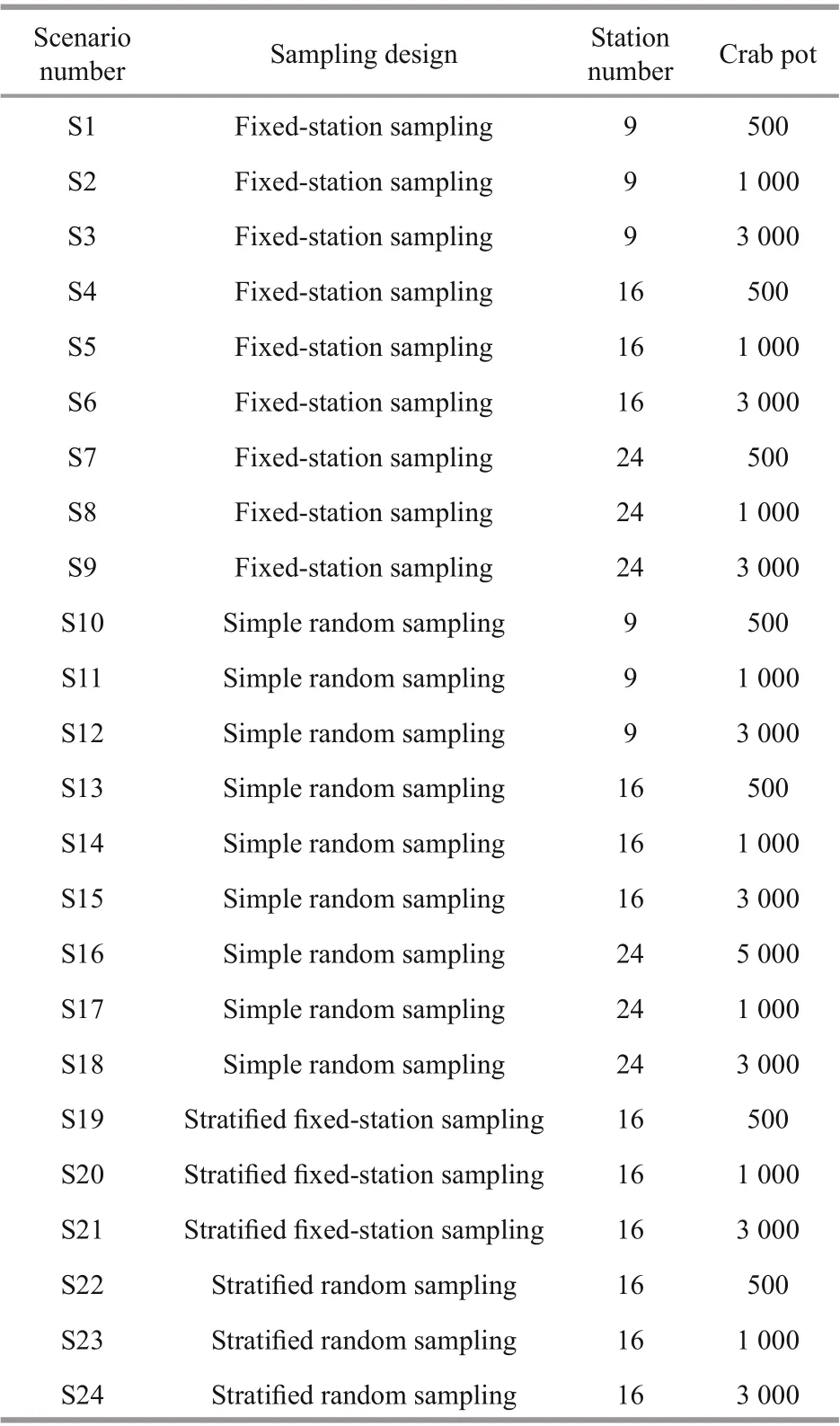
Table 1 Diff erent scenario schemes for the simulation study
3 RESULT
3.1 Determination of the soaking time
When the soaking time of crab pots was prolonged from 6 h to 10 h, the REE and RB values gradually decreased. For example, the REE value in winter decreased from 35.07% to 30.50%, and the RB value decreased from 35.05% to 30.47% (Fig.6). When the soaking time was prolonged from 10 h to 16 h, the REE and RB values increased. For example, the REE value in winter increased from 30.50% to 37.11%,and the RB value increased from 30.47% to 37.08%(Fig.6). The best simulation results occurred in 10 h.Thus in the current study, 10 h was selected as the soaking time at each sampling station during the simulation studies.
3.2 Comparison of diff erent sampling designs
The REE values of FS and SR varied from 4.21% to 113.91% and from 31.90% to 65.11%, respectively(Fig.7). Overall, FS had a wider range of REE values.The REE values of SFS and SRS varied from 1.37% to 44.96% and from 31.61% to 56.71%, respectively(Fig.7). The REEs of SFS and SRS were relatively more stable and less variable than those of FS and SR.Therefore, stratified sampling resulted in less deviation than unstratified sampling. The corresponding REE values of fixed-station sampling (FS and SFS) were smaller than those of random sampling (SR and SRS),except for the scenarios with nine sampling stations(Fig.7). For the RB values, we obtained similar results as the REE values, i.e., stratified sampling worked better than unstratified sampling. The RB values of SFS and SRS varied from -44.96% to 2.72% and from-54.02% to -4.67%, respectively. Meanwhile, the RB values of FS and SR varied from -69.97% to 113.76%and from -60.63% to -8.20%, respectively (Fig.8).
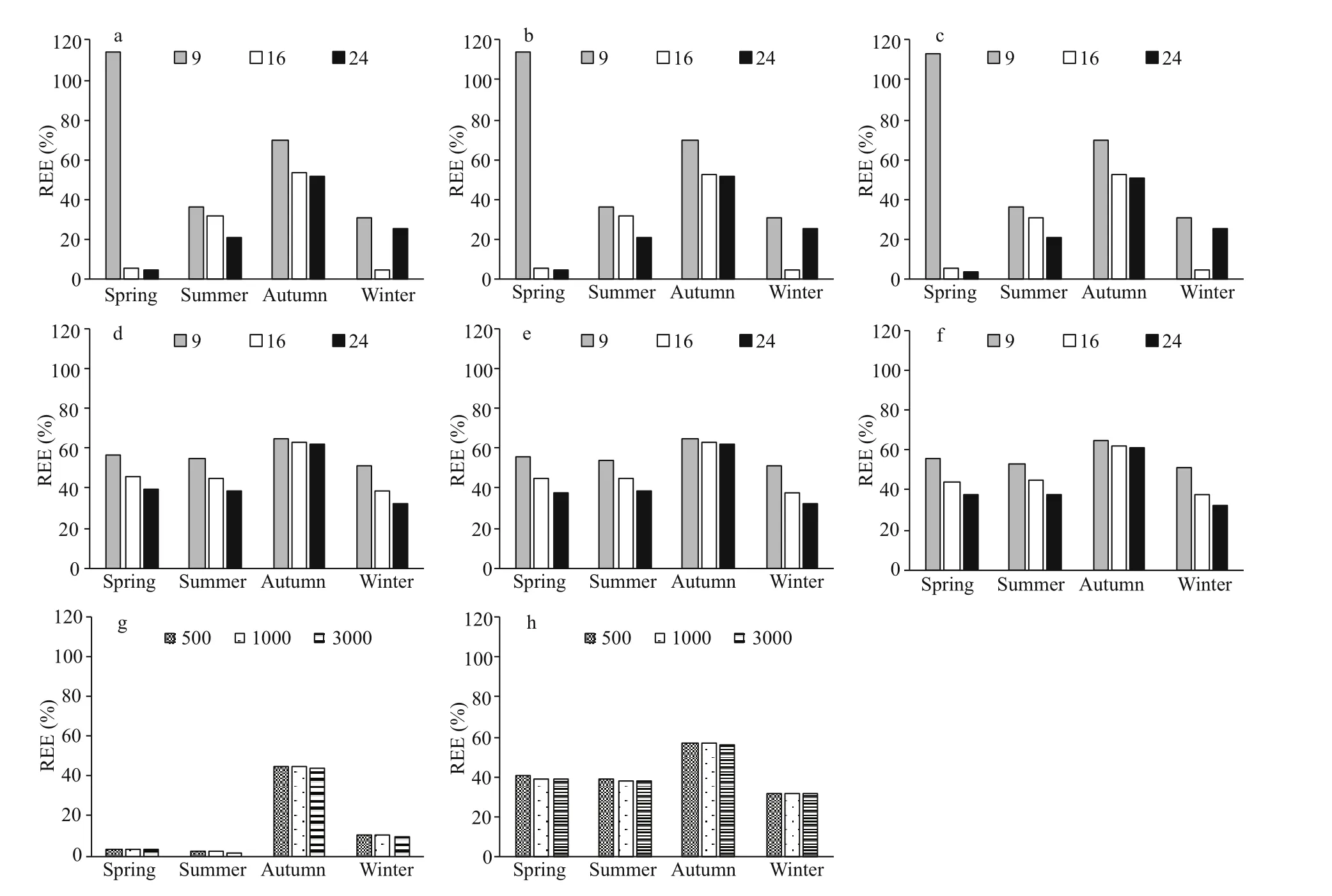
Fig.7 Relative estimation error (REE) of diff erent sampling designs (totally 96 scenarios)
3.3 Comparison of the number of sampling stations
The number of sampling stations exerted a great impact on results. The REE values of FS decreased with the increase in station numbers from 9 to 24 except for the scenario of 24 sampling stations in winter (Fig.7). However, the decrease rate was not uniform. In spring and autumn, for example, when the number of stations was increased from 9 to 16, REE decreased rapidly (spring: from 113.91% to 5.88%;Autumn: from 69.98% to 53.35). When the number was increased from 16 to 24, REE slightly decreased(spring: from 5.88% to 4.44%; Autumn: from 53.35%to 51.75%) (Fig.7a-c). The REE values of SR decreased with the increase in station number. The decrease rates were stable for all the cases (spring:55.75% to 44.62% to 38.03%) (Fig.7d-f). Overall,the RB values of FS and SR showed a similar trend with REE values (Fig.8). The RB values of FS gradually approached 0 with the increase in station numbers from 9 to 24, except for the scenarios of 24 sampling stations in winter (Fig.8a-c). In SR, all RB values were less than 0. The RB values of autumn(-60.63%) were much lower than those of the other seasons, and those of winter (-8.20%) were closer to 0 (Fig.8d-f).
3.4 Comparison of the number of crab pots
The REE values gradually decreased and RB values gradually increased as the number of crab pots was increased, but the eff ect of the number of crab pots on the results was not remarkable. The most obvious change trend occurred in SR. For the scenarios of nine stations in summer, the RB value increased from -24.43% to -18.83%. For the most cases, when the number of crab pots was increased from 500 to 3 000, the range of REE and RB values varied by less than 2%.
3.5 Eff ect of density variance of spatial distribution
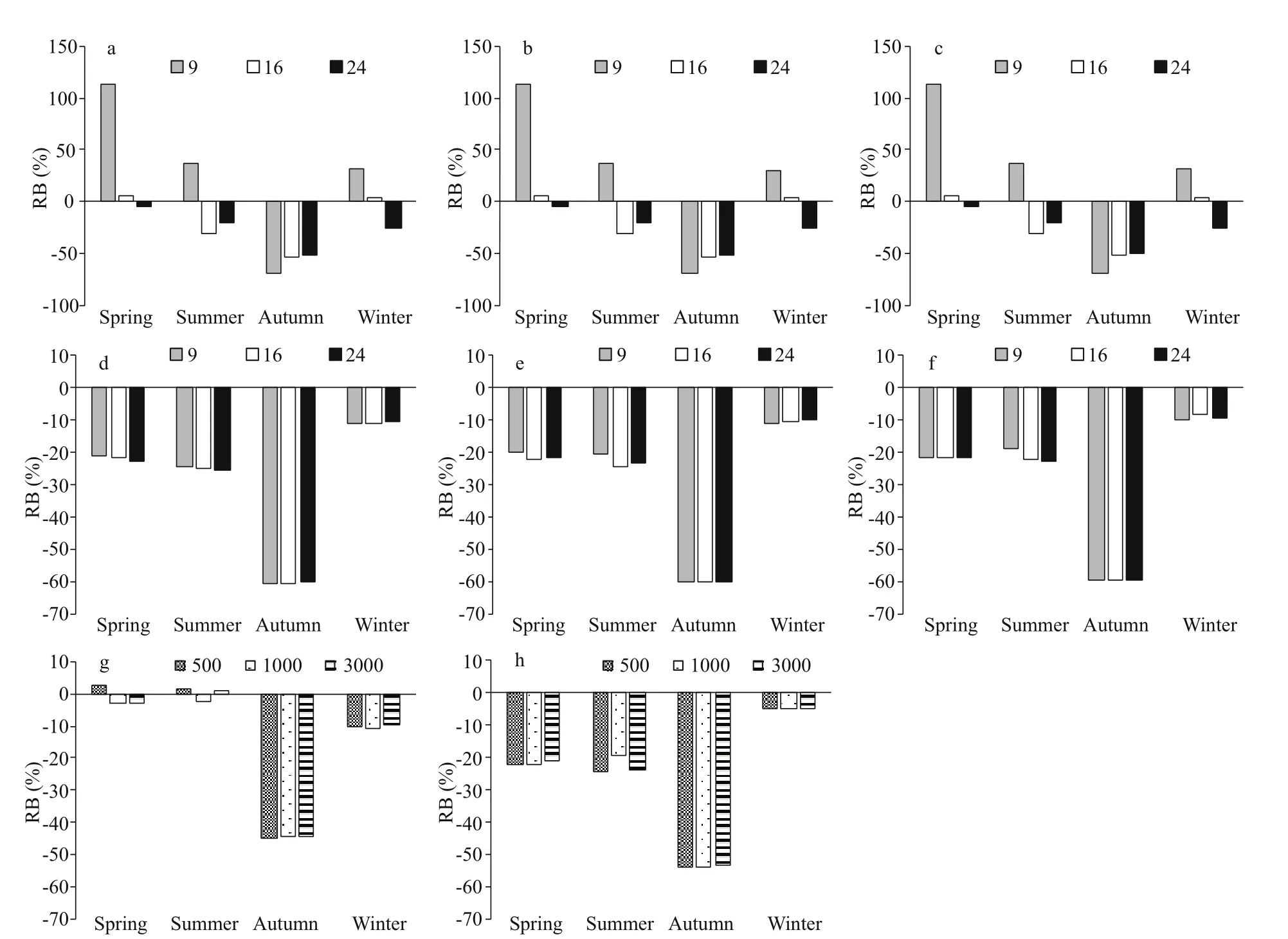
Fig.8 Relative bias (RB) for diff erent sampling designs (totally 96 scenarios)
Resource density and distribution exerted remarkable eff ects on the sampling results, especially in FS. In the current study, the density variances of the P. trituberculatus abundance in spring, summer,autumn, and winter were 38.06, 85.68, 441.11, and 8.85, respectively. The resource intensive areas appeared in spring, summer, and autumn. In winter,the resource distribution was relatively even comparing with the three other seasons. In spring, the estimated abundance values for the scenario of nine sampling stations were much higher than the “true”value (REE=113.91%) because one of the selected sampling stations was located in the center of resource-intensive areas. All the RB values in SR and SRS were negative because of the limitation of crab pot capture capacity (Fig.8). The RB values in autumn were the worst, whereas those in winter were closer to 0, and the difference between spring and summer was not remarkable (Fig.8).
4 DISCUSSION
4.1 Discussion of soaking time
The soaking time of crab pots in the sea plays an important role in P. trituberculatus resource survey.The current study results indicate that 10 h of soaking time is reasonable. Too long or too short soaking time reduces the accuracy and precision of the estimated results. In specific, a long time is needed for the bait to attract the crab into the crab pot when the pot is placed in the sea, whereas the catching effi ciency of the crab pot cannot be fully utilized in a short period(Tang and Wu, 1990). The crabs in the pot reached a certain amount with time. The catch effi ciency of the crab pot decreased (Wu, 1996).
The soaking time of crab pots is a factor aff ecting the catches of crab. Zhang et al. (2015) indicated that the soaking time of crab pots is more reasonable between 8 and 11 h. Hong et al. (1999) found that the catch of crabs increases rapidly after 1 h of crab pot soaking, peaks at 8-9 h, and then decreases with time.They deemed 9-10 h as the optimal choice. Their conclusions are consistent with our study. However,Robertson (1989) and Öndes et al. (2017) reported that the catch per unit eff ort of Scylla serrata and Cancer pagurus in the pot fishery does not increase remarkably with the soaking time. This phenomenon may be due to the differences in species, fishing gear,and fishing methods.
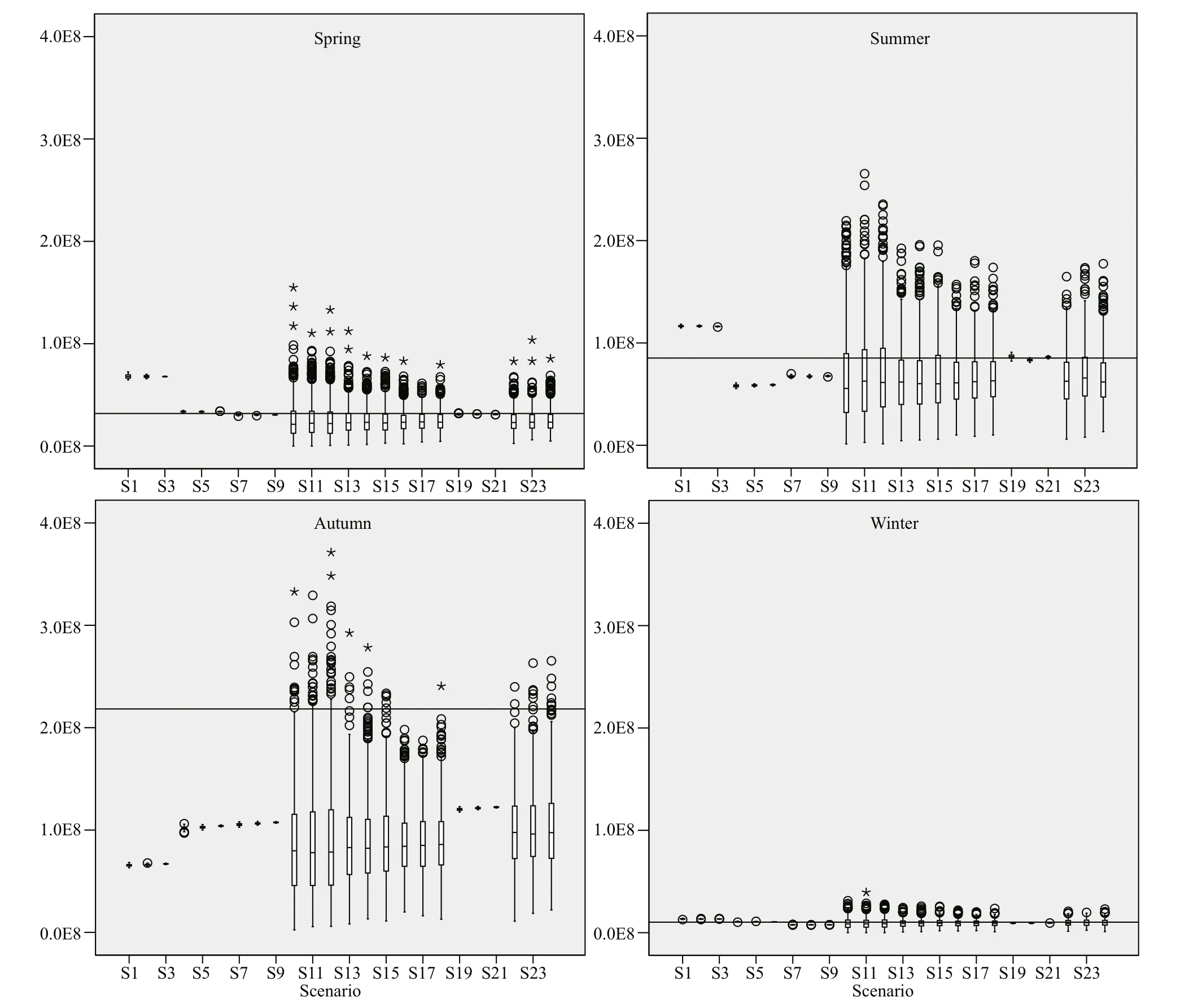
Fig.9 Box plot of the P. trituberculatus abundance simulated 1 000 times for each season in all simulated sampling designs
4.2 Sampling design selection
The REE and RB values of FS varied greatly between seasons and station number (Fig.7a-c;Fig.8a-c). Reasonable station selection can produce accurate simulation results. Therefore, the selection of sampling stations in FS is particularly important. If the resource distribution is stable, FS is reasonable because it can reflect the annual change of the resource(Wang et al., 2018; Sun and Wang, 2019). The distribution ofliving resources may be extremely uneven and constantly moving in diff erent seasons.Thus, FS should be the final choice if other sampling designs can be made.
The REE values of SR were stable and gradually decreased as the number of stations was increased when compared with FS because SR can reduce the intervention of subjective factors and make the results more objective (Figs.7 & 8). However, the simulation results of SR showed a large deviation because of the randomness of simple random sampling, and almost all the outliers appeared in SR (Fig.9). The deviation of FS was small because FS only repeated the sampling procedure 1 000 times at the fixed stations(Fig.8). A previous study obtained similar simulation tests for bottom trawl and obtained the same conclusion that the deviation of SR is large (Sun and Wang, 2019). In a word, SR is more suitable for areas with uniform distribution of resources or exploring resources in the study area.
In this study, the stratified sampling (SFS, SRS)had advantage over unstratified sampling (FS, SR).Many relevant studies obtained the same conclusion that stratified sampling works better than unstratified sampling under the same conditions because it can obtain more accurate results (Yuan et al., 2011; Liu,2012; Zhao et al., 2014). In stratified sampling, the definition of strata directly aff ects the quality of the estimated abundance, and proper strata can yield good results, which would otherwise be worse than those of unstratified sampling (Smith and Gavaris,1993; Li, 2010; Yuan et al., 2011). In our simulation,the results of stratified sampling with 16 stations were not only better than those of unstratified sampling with 16 stations but also better than those of 24 stations, which was more obvious in the scenarios of FS (Fig.7). Stratified sampling can reasonably allocate stations, make diff erent sampling effi ciencies among diff erent strata, and thus improve sampling accuracy(Gavaris and Smith, 1987; Chen et al., 2006).
4.3 Determination of the station number
Many studies have also shown the same conclusion that more stations can obtain higher-quality survey data (Lai and Kimura, 2002; Sun and Wang, 2019).However, too many sampling stations not only increase the funding and time but also generate redundant information, which reduces the precision and accuracy of estimated results (Zhao et al., 2014).Moreover, oversampling damages the biological resources and ecological environment of the surveyed area (Conners and Schwager, 2002). The REE values of SR gradually decreased when the station number was increased from 9 to 24, and a slight difference was observed between seasons. However, large errors appeared in FS with nine sampling stations. The same results as above also appeared in our previous sampling design study on trawling (Sun and Wang,2019). Therefore, 24 stations can obtain viable survey data in this study, and 16 stations are necessary if the fund and time are limited. Nine stations are feasible to SR, but 16 stations are necessary for FS. Abnormal results appeared in S9 in winter because the resources in winter were fewer than those in the three other seasons, and too many sampling stations generated redundant information.
4.4 Selection of the number of crab pots
Three diff erent numbers of crab pots in each station(500, 1 000, and 3 000) were set to explore the impacts of the number of crab pots on the estimated abundance of P. trituberculatus and choose a reasonable number of crab pots. Other scholars, such as Zhang et al.(2015), Tang and Wu (1990), Ye (2001), and Lin et al.(2013), used 50, 300, 500, and 3 000 crab pots for resource surveys, respectively. According to the current study, the number of crab pots exerted no remarkable eff ect on the simulation results. Therefore,when using crab pots to investigate the resources of P.trituberculatus, a small amount of crab pots can still achieve similar results with a large number of crab pots. A small number of crab pots should be selected from the perspective of saving time and funding or protecting fishery resources and the environment. In addition, a small amount of crab pots can improve the safety of fishing boats (Zeng, 2016).
4.5 Density of resource
The distribution of fishery resources changes and individuals are not distributed in the entire sea area because of the influence of environmental and human factors (Zhang et al., 2017). Temporal factors are closely associated with resource production (Wang et al., 2012). In spring, summer, and autumn,P. trituberculatus has obvious resource-intensive areas, especially in autumn. In winter, the resources of P. trituberculatus are evenly distributed. Therefore,a certain proportion of zero value and high catch value appeared in the survey month, which aff ected the mean value and variance of the estimation results and then aff ected the accuracy of resource estimation.
The abundance of P. trituberculatus in autumn was much higher than that in other seasons but much lower than the “true” value in autumn (Fig.9). This finding can be attributed to the fact that as a passive fishing gear, crab pot has the upper limit ofits catching capacity. The external crabs will not enter the crab pot when the number of crabs in the pot reached the capture capacity (Tang and Wu, 1990). In addition,the freshness of the bait and the competitive behavior to the territory will also aff ect the catching ability of the crab pot (Wu, 1996). Therefore, when using crab pots for fishery resources survey, it is necessary to attach great importance to seasons with high resources or resource-intensive areas. In these cases, the limitations of crab pots may cause underestimation of resources.
The previous relevant studies neither used statistical methods nor involved the catches based on the probability algorithm. In the current study, we established a statistical algorithm to calculate the probability that each individual can be caught in the study area, which is more consistent with the actual situation. In addition, some scholars reported that fishery-specific factors, such as pot design, escape gaps, freshness of bait, and agonistic interactions among conspecifics inside and at the entrance of pots,influence the catchability of crabs in the pot fishery(Miller, 1979; Brown, 1982; Smith and Jamieson,1989). Some of these factors will be considered in our future works.
5 DATA AVAILABILITY STATEMENT
All data generated and/or analyzed during this study cannot be shared at this time as the data also forms part of an ongoing study.
6 ACKNOWLEDGMENT
The authors are grateful for all scientific staff and crew for their assistance with data collection during all the surveys.
 Journal of Oceanology and Limnology2021年2期
Journal of Oceanology and Limnology2021年2期
- Journal of Oceanology and Limnology的其它文章
- Predicting sediment flux from continental shelfislands,southeastern China*
- Laboratory simulation of dissolved oxygen reduction and ammonia nitrogen generation in the decay stage of harmful algae bloom*
- Development of high-resolution chloroplast markers for intraspecific phylogeographic studies of Phaeocystis globosa*
- Effects ofiron and humic acid on competition between Microcystis aeruginosa and Scenedesmus obliquus revealed by HPLC analysis of pigments*
- Effect of river plume on phytoplankton community structure in Zhujiang River estuary*
- Exploring the sublethal genotoxic effects of class II organophosphorus insecticide quinalphos on freshwater fish Cyprinus carpio
