基坑开挖对下卧管线竖向变形影响的数值分析
吴 峥, 姚黎芳, 陈学良, 张恒志, 徐长节,3,4*
(1.杭州市市政设施监管中心, 杭州 310003; 2.浙江大学滨海和城市岩土工程研究中心, 杭州 310058; 3.华东交通大学-土木工程国家实验教学示范中心, 南昌 330013; 4.华东交通大学江西省岩土工程基础设施安全与控制重点实验室, 南昌 330013)
目前,城市不断发展地下停车场、地下街道、地下综合管廊等多种地下空间,由此产生了许多新建基坑工程。同时,城市地下空间已经运营着大量地铁隧道及各类管线,使得新建基坑上跨于既有运营隧道或管线的情况越发普遍。基坑内土体的卸荷会改变周边土体应力场和位移场,从而引起下卧隧道或管线产生附加应力及变形,影响运营隧道或管线的安全。
许多学者通过理论推导、数值模拟及实测分析的方法,研究了基坑开挖引起下卧隧道或管线变形位移的问题。在理论推导方面,姚燕明等[1]考虑残余应力的影响,通过地基沉降计算公式给出基坑开挖引起下卧区间隧道及地下管线的变形计算方法;陈郁等[2]采用Mindlin弹性半空间应力解和弹性地基梁理论得到了求解下卧隧道隆起量的计算方法;欧雪峰等[3]综合考虑了土体卸荷和基坑降水的影响,基于Mindlin解和Pasternak双参数模型提出了一种计算下卧隧道变形的解析计算方法。在数值模拟方面,Zheng等[4]基于平面应变假设,应用有限元软件ABAQUS/Standard建立二维数值模型,研究了不同开挖深度以及隧道离坑底不同垂直距离情况下隧道的变形情况;张玉成等[5]结合海珠广场发展项目基坑工程,利用三维有限元程序Ansys建模,对该工程下方地铁隧道的变形及管片附加应力进行了详细的分析;李平等[6]用FLAC3D模拟了南京火车站站前广场龙蟠路隧道西段施工全过程,总结出了下卧隧道的变形规律,并对不加固、桩板支护和旋喷桩满堂加固三种工况进行了对比分析,得到了三种工况下隧道的变形规律;Shi等[7]用ABAQUS建模对基坑施工引起下卧既有隧道的影响进行了详细的参数分析,包括基坑长短边尺寸、基坑开挖深度、土层密度、隧道刚度,总结出了基坑施工对下卧隧道变形的一般规律。在实测分析方面,陈郁等[8]通过分析上海某基坑上跨既有隧道的监测数据,得到了下卧隧道的隆沉变化规律。
综上,目前很少有从管线与基坑之间的夹角出发研究基坑开挖引起下卧管线的变形。当基坑与管线处于不同夹角时,探究管线的隆沉位移可以得出下卧管线的变形机理,同时也可以比选出实际工程的最优方案。因此,以杭州市沿江大道管廊基坑工程上跨污水管段为依托,利用ABAQUS建立三维有限元模型对该实际工程进行模拟,在此基础上分析了管线周围土体注浆加固的作用,并通过改变管线与基坑夹角的角度,研究了下卧管线的变形规律。
1 工程概况
杭州市沿江大道综合管廊基坑位于钱江新城二期扩容区块内,管廊西起观潮路,东至和睦港,全长约3 650 m,主要布置在沿江大道北侧绿化带内,局部布置在道路车行道范围内。
基坑位于污水管正上方,且与污水管斜交,夹角约60°;基坑底与污水管垂直净距1.0 m,两根污水管轴心距为5.3 m。管廊基坑与现状污水管的位置关系如图1所示,本段污水管为两根重力管,内径2.4 m,管壁厚0.18 m,设计坡度0.6‰,设计流速1.66 m/s,管道工作压力0.06 MPa。

图1 管廊基坑上跨污水管平面图Fig.1 Plan view of sewage pipe underneath foundation pit
1.1 基坑支护及加固方案
基坑开挖深度约5.0 m,采用放坡结合土钉墙支护开挖。墙面坡度1∶0.3,坡面喷射100 mm厚的C20素混凝土,内设φ8 mm@200 mm×200 mm钢筋网。土钉采用φ20 mm钢筋,根长5~12 m,成孔直径120 mm。基坑支护横剖面如图2所示。

图2 管廊基坑支护横剖面图Fig.2 Profile of foundation pit support
由于基坑位于管线正上方,基坑内土体卸荷容易引起管线上浮。工程设计中考虑对污水管两侧3 m、管顶0.5 m范围内进行注浆加固土体,加固土体28 d无侧限抗压强度大于0.8 MPa。注浆钢花管不予拔除,基坑开挖后,铺设钢筋网片,钢筋网片与钢花管焊接或扎紧后及时浇筑混凝土封闭基坑,减少污水管上浮。污水管注浆加固如图3所示。
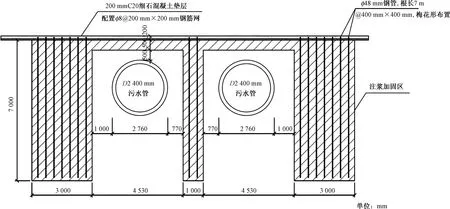
图3 污水管加固图Fig.3 Reinforcement of sewage pipe
1.2 场区地层条件
本场区地层自上而下分为:①1杂填土层,平均厚度5.1 m;①2素填土层,平均厚度5.5 m;③4砂质粉土层,平均厚度2.5 m;③5粉土夹粉砂层,平均厚度2.3 m;③6粉砂夹粉土层,平均厚度9.0 m;⑥1淤泥质粉质黏土夹粉土层,平均厚度为4.2 m;⑥2淤泥质粉质黏土层,平均厚度2.5 m。各土层的物理力学指标如表1所示。

表1 土体分层及物理力学指标Table 1 Physical and mechanical properties of soils
2 三维有限元模型及验证
2.1 有限元模型的建立
利用ABAQUS建立三维有限元模型,基坑开挖尺寸为20 m×11.3 m×5 m,为消除边界效应对计算结果的影响,取模型侧边边界范围为4倍基坑开挖深度,底边边界范围为5倍基坑深度,本次模型尺寸取为50 m×50 m×30 m。几何模型如图4所示,污水管与加固区的位置关系如图5所示。

图4 管廊基坑上跨污水管三维有限元模型Fig.4 Three-dimensional finite element model of pipe underneath foundation pit

图5 管线与加固区位置示意图Fig.5 Relative position between pipe and reinforcement
为方便计算,对模型作如下假设:①同一土层中,土体是均匀、连续、各向同性的;②土体是理想的弹塑性体;③管道、土钉是材料均匀的线弹性体。
模型网格如图6所示,土体单元采用C3D10实体单元,选用Mohr-Coulomb模型;土钉单元采用T3D2桁架单元;面层采用C3D10实体单元;管道单元采用S3壳单元。

图6 数值分析模型网格图Fig.6 Mesh of model for numerical simulation
2.2 计算参数的确定
土层所采用的计算参数见表1,土钉、面层及管道的计算参数见表2。基坑开挖对开挖面以下土体产生了竖直方向的卸荷作用,导致坑底土体产生回弹现象,要正确计算或描述这种回弹位移与卸荷量之间的关系,卸荷模量的取值尤为重要。文献[9]研究表明,软土卸荷模量远大于常规三轴试验所获得的压缩模量或弹性模量,而本文所使用的Mohr-Coulomb模型是弹-完全塑性模型的一种,它认为土体在达到抗剪强度之前的应力-应变关系符合虎克定律,不能区分加荷和卸荷,故使用弹性模量以该本构模型进行计算得到的回弹量会偏大。文献[10-11]将卸荷模量作为输入参数以减少Mohr-Coulomb模型模拟卸荷带来的误差,研究表明使用该方法能得到较合理的结果。参考文献[5]中对卸荷模量的取值,取弹性模量的1.3~1.7倍作为输入参数进行计算。

表2 结构计算参数Table 2 Structural parameters for computation
2.3 施工步骤的模拟及结果验证
利用ABAQUS中Model change功能控制单元的“生死”来模拟基坑的开挖。大量对实际工程进行数值模拟文献的表明,施工步骤的模拟接近实际工况步骤常常能得到与实测值相符的计算结果,且所得到的计算结果有很好的参考意义。故本文施工步骤按照实际工况进行模拟,实现施工全过程的动态模拟。具体数值模拟步骤如表3所示。

表3 数值模型关键工况Table 3 Numerical simulation steps
由于左右两侧管线位移基本一致,故仅以左侧管线为研究对象。图7为左侧管线的隆沉位移计算值与实测值对比图,可以看出,两者变形趋势基本吻合。由于上方土体的开挖卸荷,使得管线呈现出“中间大、两边小”的上凸型变形模式,且在基坑开挖范围内隆起变形较为显著,在基坑中心处达到最大值。其中计算最大隆起量为3.23 mm,实测最大隆起量为2.91 mm,两者相差11%。由于数值模型未能考虑基坑围护结构中其他部分的加固作用,导致计算值整体略大于实测值。

图7 左管线隆起位移计算值与实测值对比Fig.7 Comparison between the calculated and measured heave displacement of the left pipe
3 敏感性因素分析
3.1 注浆加固对管线位移的影响
为了研究注浆加固土体对于保护管线的作用,还设置了管线周围土体未加固的工况。如图8所示,通过计算得到两种工况下左侧管线隆起位移量,两种工况管线均呈现“上凸型”变形模式,最大值均出现在基坑中心,且加固工况的管线隆起量均小于未加固工况。因此对下卧管线周围采用注浆加固能有效减少基坑开挖引起的管线隆起变形,且在加固区范围内,这种效果更加明显。

图8 两种工况下左线管道隆起位移对比Fig.8 Comparison of heave displacement of left pipeline under two working conditions
在模型中选取平行于基坑长边方向的剖面1-1(图6),模拟管线周围土体加固与未加固的两种工况,分析基坑坑底土体沿剖面1-1的回弹变化。如图9所示,当土体未加固时,坑底回弹变形为三峰曲线,曲线上两个波谷刚好对应管线所在位置,这是由于管线刚度比土体刚度更大,管线和周围土体起到限制土体位移的作用,管线位置的坑底回弹较小,且由于管线距离坑底较近,限制土体位移的作用比较明显。而在注浆加固后,坑底回弹曲线变为了双峰曲线,且回弹量整体减少,峰值出现在加固区的两侧,加固区内的坑底回弹则趋于一致,坑底最大回弹量减少了2.45 mm。由此可知,该注浆加固方式使得加固区内整体刚度增加,但对加固区外的影响较小。
3.2 管线与基坑夹角对管线位移的影响
为研究管线与基坑夹角对管线位移的影响,本文以未加固工况为基础,通过改变单根管线与基坑长边的夹角,设计了如图10所示的七个不同夹角方案。基坑长短边比为1.73,当夹角为30°时,管线轴线刚好与基坑对角线重合。

图10 管道与基坑不同夹角情况示意图Fig.10 Schematic diagram of different intersection angles between pipe and foundation pit
图11为夹角为0°、30°、60°及90°四个方案计算所得管线隆起变形,可以看出,当夹角为0°时,管线的整体位移最大;当夹角为90°时,管线的整体位移最小。这与参考文献[7,12]得出的结论一致,即在基坑尺寸固定的情况下,管线与基坑长边垂直时,管线的隆起变形最小。
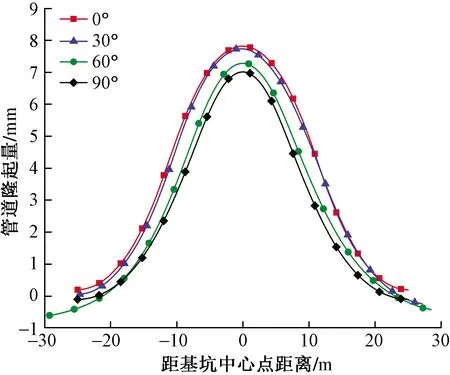
图11 不同夹角情况下左线管道隆起位移对比Fig.11 Comparison of heave displacement of left pipeline under different angle conditions
值得注意的是,0°夹角与30°夹角引起的管线隆起相差很小,为更直观的分析管线与基坑长边夹角对管道隆起的影响,以夹角值为横坐标,分别以图10中七个夹角方案计算所得管线最大隆起量和基坑范围内管线长度为纵坐标绘制图12、图13。
如图12、图13所示,当管线与基坑长边夹角在0°~30°范围内时,下卧管线最大隆起量与其在基坑开挖范围内的长度负相关,随着基坑范围内管线长度的增加,下卧管线最大隆起量在减少,这是因为夹角在0°~30°范围内时,随夹角值的增加,尽管基坑范围内管线长度在缓慢增加,但管线更靠近基坑刚度较大的角部,使得管线隆起量最终呈现出随夹角值增加而缓慢下降的趋势。而当管线与基坑长边夹角在30°~90°范围内时,基坑范围内管线的长度和管线的最大隆起量均随夹角值的增加而呈现出一致的下降趋势,此时下卧管线最大隆起量与其在基坑开挖范围内的长度正相关,这与参考文献[13]中相关结论一致,在30°~90°范围内时,随夹角值的增加,基坑范围内管线长度在显著减少,此时该因素占主导地位,使得最终管线的最大隆起量随夹角值变化的趋势和基坑范围内管线长度随夹角值变化的趋势一致。

图12 管线与基坑夹角对管线最大隆起位移的影响Fig.12 Effect of angle between pipeline and foundation pit on maximum uplift displacement of pipeline
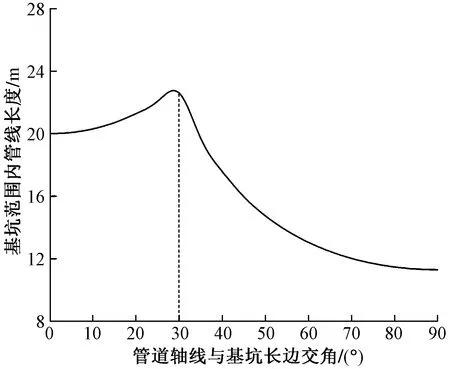
图13 管线与基坑夹角对基坑范围内管线长度的影响Fig.13 Effect of angle between pipeline and foundation pit on length of pipeline under foundation pit
4 结论
以杭州市沿江大道管廊基坑工程上跨污水管段为依托,利用ABAQUS建立三维有限元模型对该实际工程进行模拟,在此基础上分析了管线周围土体注浆加固的作用,并通过改变管线与基坑的夹角,研究了不同夹角的下卧管线变形情况,得出了以下结论。
(1)由于上方基坑的开挖,会使下卧管线呈现出“中间大、两边小”的上凸型变形模式,且在基坑中心处隆起位移最大。
(2)在坑底未加固时,下卧管线的存在会限制土体回弹变形,减小管线上方坑底的隆起量。对下卧基坑管线周围进行合理的注浆加固,能有效地减少管线整体隆起变形。
(3)在基坑尺寸固定的情况下,当管线与基坑长边垂直时,管线的隆起变形最小。本文所研究基坑的长短边比为1.73,下卧管线与基坑长边夹角的增加会使管线的隆起量减小,且在0°~30°时减小速度较缓,30°~90°时减小速度较快。 在实际工程方案比选中,应尽量选择管线与基坑长边垂直或管线与基坑长边交角大的方案,可以减少管线的隆起变形。
本文仅考虑了下卧管线与基坑长边交角对长短边比为1.73基坑的影响,对于其他长短边比的基坑还需要作进一步的探讨研究。

