低层装配式竖缝中空剪力墙抗震性能

申彦利, 石佩云

(1.河北工程大学土木工程学院，邯郸 056000； 2.河北省装配式结构技术研究中心，邯郸 056000)

近年来，随着中国产业结构的调整和相关政策的出台，传统的建筑方式面临革新，建筑产业化成为行业热点，大力推广装配式建筑是实现产业化的途径之一。在装配式结构形式中，装配式剪力墙结构占据装配式结构的90%[1]，改善传统装配式剪力墙结构的抗震性能，成为学者研究的热点之一。

为改善其受力性能，相关学者做了许多有益的尝试，如组合耗能填充剪力墙[2]、摇摆耗能剪力墙[3]等。对于相同受力形式的构件也作了改进，范栋鑫等[4]通过对带有横槽的桥墩进行抗震性能分析，结果表明，带有直槽的桥墩抗震性能及受力性能较好，说明带有横缝的桥墩可以有良好的耗能性能；王宇亮等[5]研究了采用阻尼器连接的竖缝剪力墙在低周反复加载下抗震性能，结果表明阻尼器在受力过程中进行耗能，承载力与现浇结构相差不大；秦士宏等[6]对竖向拼缝剪力墙抗震性能进行研究，试验结果表明竖向拼接缝对于构件的延性及耗能有显著的提升。目前，对于装配式结构的研究多为构件之间的连接方式，或者利用外加阻尼器进行耗能研究，成本较高，而对于利用构件自身改变抗震性能，少有学者研究，不够系统完善，因此，在前人的研究基础上，提出了新型装配式竖缝中空剪力墙为验证新型装配式竖缝中空剪力墙的抗震性能，通过有限元软件研究不同缝间墙高宽比对墙体抗震性能的影响，为该类结构体系提供设计依据。

1 低层装配式竖缝中空剪力墙的构造

为了进一步研究抗震性能更优的低层装配式剪力墙，本文提出了装配式竖缝中空剪力墙结构，这种形式的装配式剪力墙构造如图1所示。

图1 装配式竖缝中空剪力墙示意图Fig.1 Detailed of assembled vertical seam hollow shear wall

(1)墙体中有单块矩形孔洞，即去除实心墙体墙身的部分混凝土，矩形孔洞居中布置，减少了墙体的自重，进而减少结构在地震中吸收的能量。

(2)在墙体的前后设有贯穿的人工竖缝，将整块墙体分成若干小墙肢。

(3)墙体的端部设有边缘构件暗柱，暗柱的设置可以减小墙体的刚度退化。

剪力墙中间的矩形孔洞以及竖缝间放入保温板，不仅可以减少墙体热传导，使墙体具有一定的节能效果，还加快了施工速度，单块矩形孔洞周围两侧双向布筋，开缝处钢筋按照规范进行加固处理。

2 数值模型

2.1 模型计算简图及基本假定

利用有限元软件建立了4片缝间墙高宽比分别为3、4、6、8的装配式竖缝中空剪力墙数值模型，为墙体分析对比简洁明确，设定竖缝的高度h与竖缝间距b的比值为n，即

(1)

运用有限元软件进行竖缝中空剪力墙模型在低周反复荷载下的数值模拟对比，计算模型如图2所示。模型由加载梁、墙体以及地梁三部分组成，墙体下端固定，墙体的竖向分布筋直接锚固在加载梁和地梁中，最后浇筑混凝土，使三者融为一体,对计算模型做了如下假定。

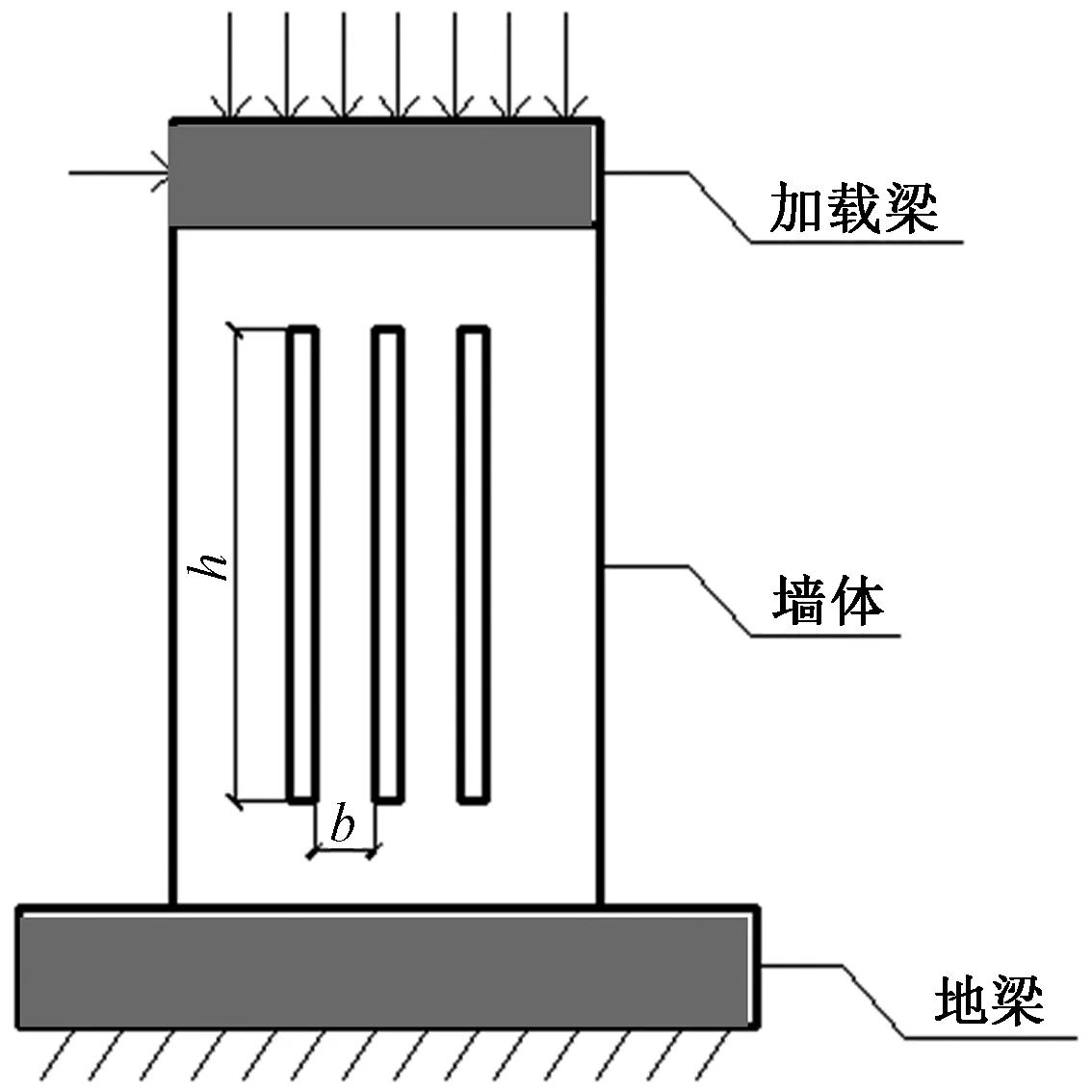
图2 装配式竖缝中空剪力墙计算模型Fig.2 Calculation sketch of assembled vertical seam hollow shear wall

(1)将墙体上部竖向荷载和水平位移荷载简化为集中荷载作用于墙体顶部的加载梁。

(2)加载梁、墙体与地梁之间采用刚性连接，地梁与地面完全固定。

(3)不考虑结构的二阶效应。

2.2 模型有效性验证

为验证模型的有效性，以文献[7]中的一片实心剪力墙为参考，通过对模型进行低周反复加载，得到模型与原试验的荷载-位移曲线对比如图3所示,各个阶段特征参数数值对比如表1所示。

表1 数值模拟和试验结果特征参数对比Table 1 Feature point paramerers of comparison of numerical simulationand test results

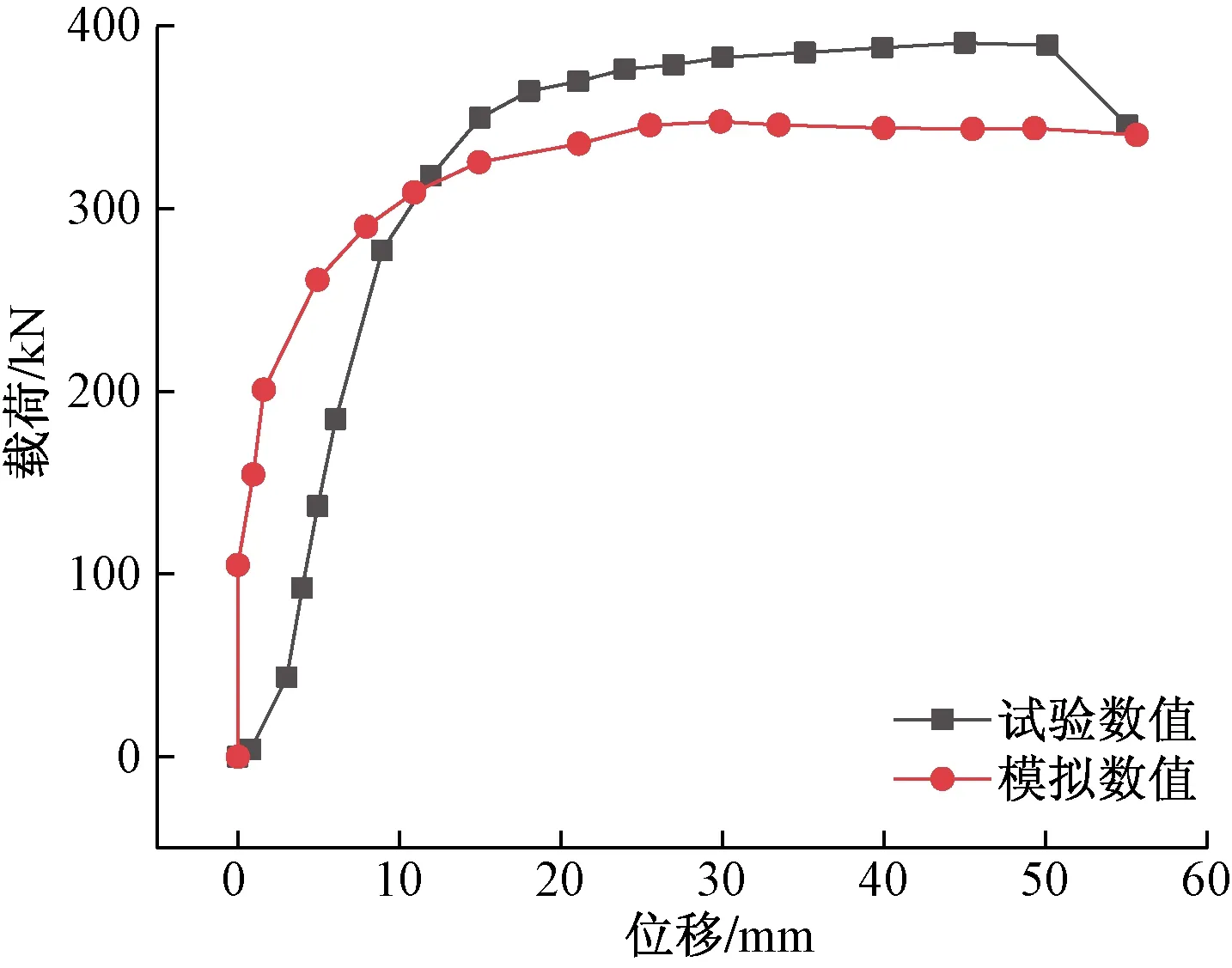
图3 试验与数值模拟荷载-位移曲线对比Fig.3 Comparison of simulation and test results of shear wall load displacement curve

实测数据是利用竖向加载装置带有反力横梁、竖向液压千斤顶、千斤顶与反向横梁之间的滑板和分配梁等所测得。固定墙体采用地锚螺栓和压梁,将地梁固定在结构实验室的地面；同时为防止在加载过程中试件产生水平位移，采用机械千斤顶挤压地梁的两端的横截面，同时压试件地梁两端的机械千斤顶，防止试件在施加水平力时发生移动。

由图3可知，有限元分析得到的曲线，初始刚度较大，导致屈服位移减小，这是因为模拟时将混凝土视为连续均匀的材质，而实际是非均匀材料，且试验仪器与构件间也存在一定的误差。由表1数据可知，剪力墙各个特征点的数值与试验相差在11%以内，模拟的荷载-位移曲线与原试验中的曲线吻合较好，整体变化趋势相同，因此认为数值模型的建立是有效的，能够模拟竖缝中空剪力墙在地震作用下的受力。

2.3 数值模拟试件设计与参数

为研究墙体抗震性能与缝间墙高宽比(n)的关系，将墙体模型以缝间墙高宽比为变量，标号为ZW1 、ZW2 、ZW3 、ZW4。根据《建筑抗震设计规范》[8]，进行剪力墙墙体尺寸的设计与计算，墙体尺寸为1 650 mm×2 600 mm×200 mm，加载梁尺寸设计为1 650 mm×400 mm×250 mm，地梁尺寸为2 850 mm×450 mm×400 mm，其中单块矩形中空孔洞尺寸为1 000 mm×2 600 mm×50 mm,配筋及构造要求参照规范确定[9]，具体见表2，竖缝条数及尺寸见表3，剪力墙数值模型中所有的钢筋均选用HRB400钢筋， 质量密度为7 800 kg/m3，钢筋均采用三级钢。假定钢筋受拉弹性模量与受压弹性模量相等，均为2×105MPa；为准确模拟模型低周反复加载下的响应，取C30级混凝土的弹性模量为3×104MPa，泊松比为0.2，钢筋的力学性能见表4，图4为装配式竖缝中空剪力墙的墙体配筋图，中间为贯穿墙体的竖缝，竖缝周钢筋加固按照规范进行。

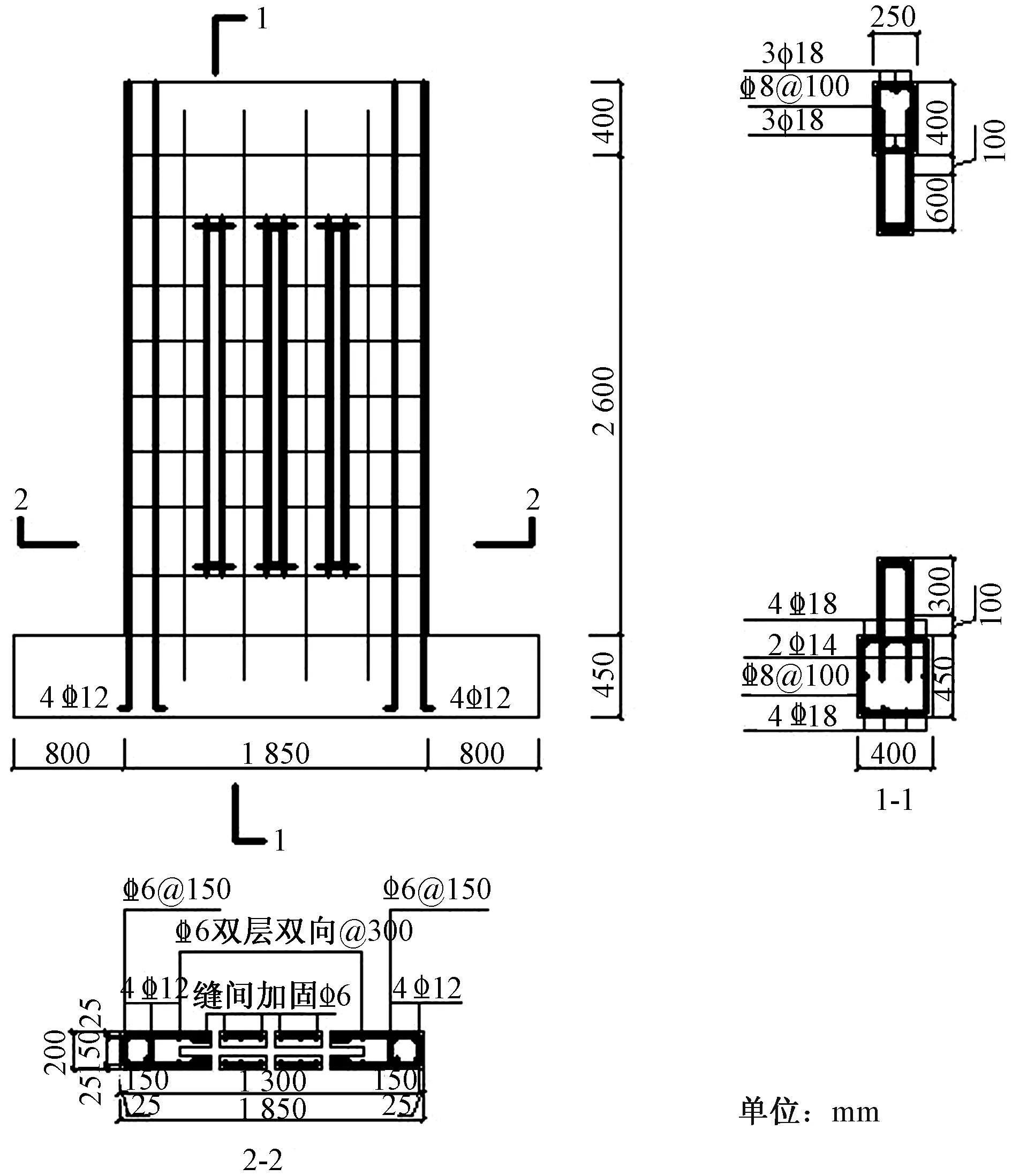
图4 ZW4墙体配筋详图Fig.4 Detailed drawing of reinforcement of ZW4 shear wall

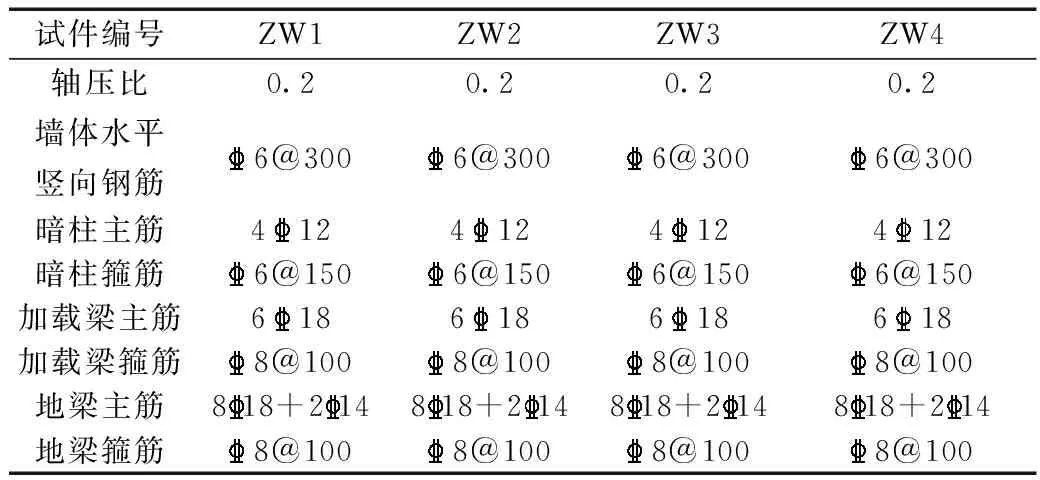
表2 模型具体参数Table 2 Model specific parameters

表3 剪力墙竖缝尺寸Table 3 Vertical seam hollow shear wall

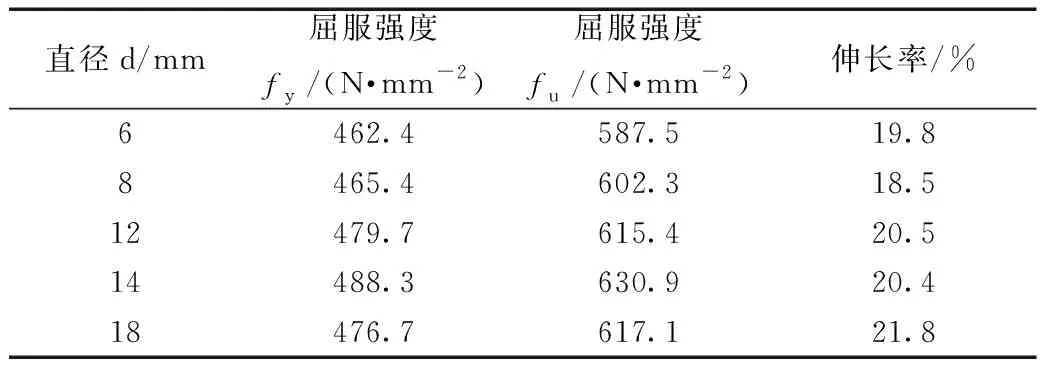
表4 钢筋力学性能Table 4 Mechanical properties of reinforcement bars

2.4 单元选取和本构关系

混凝土采用C3D8R单元，钢筋选用T3D2单元，有限元软件中，混凝土损伤塑性模型是假定其因各向同性的压碎和拉裂而导致的连续损伤模型。

根据规范[9]规定，确定混凝土的受压和拉伸的损伤因子dc以及dt，钢筋本构关系采用双斜线模型。

(2)

(3)

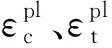
混凝土受压损伤因子dc和受拉损伤因子dt与开裂应变εin的关系图5、图6所示。

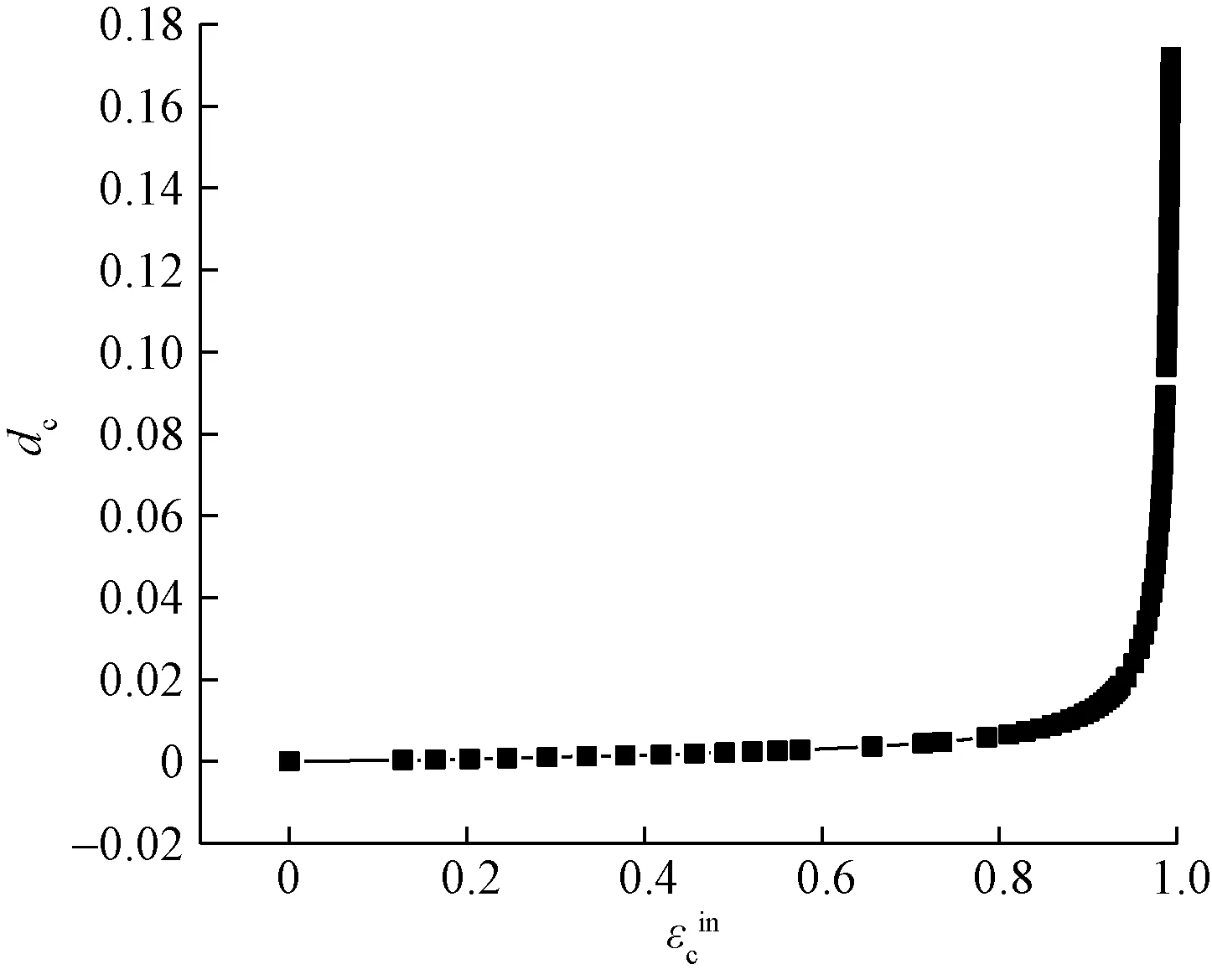
图5 dc与的关系Fig.5 Relationship of dc and

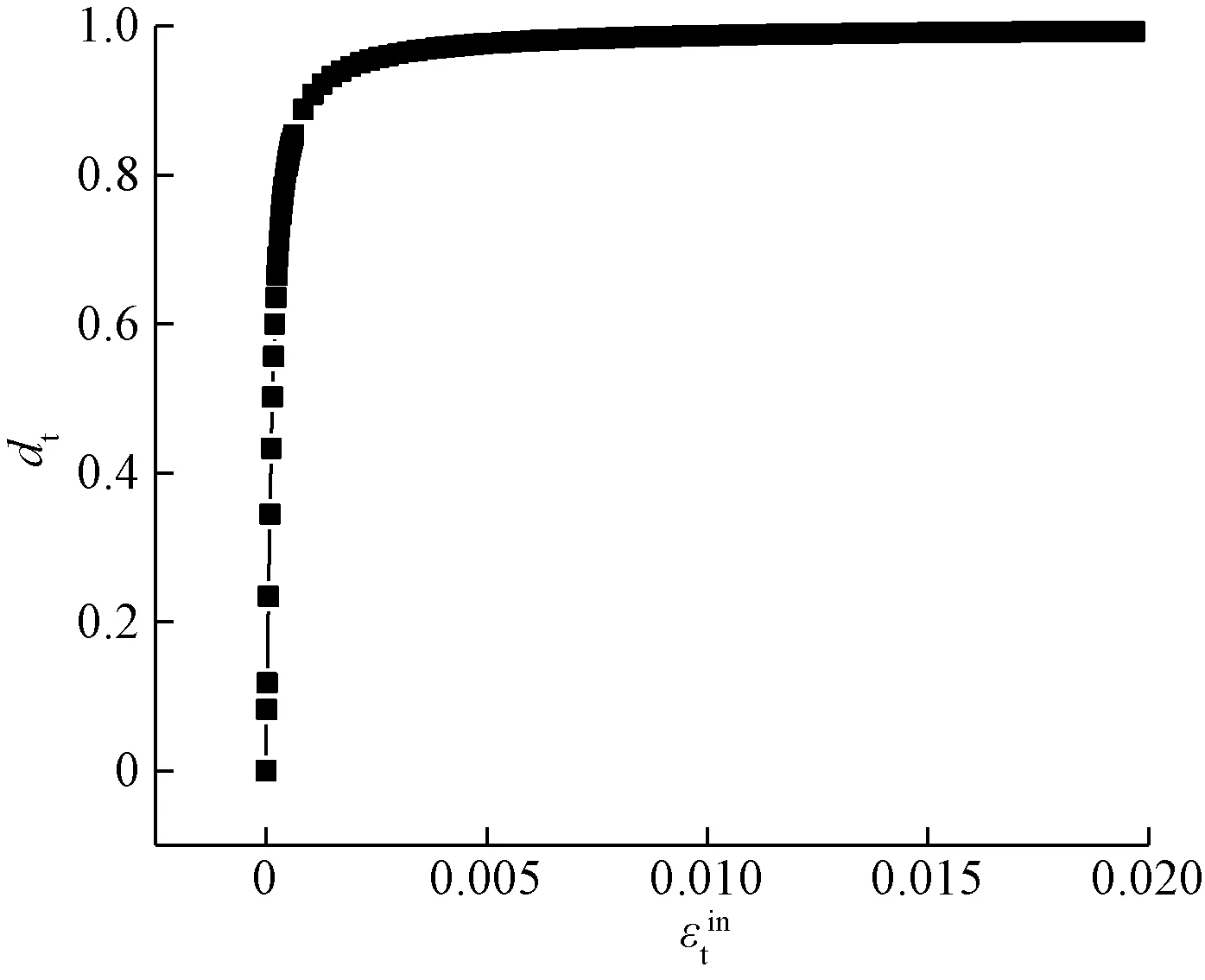
图6 dt与的关系Fig.6 Relationship of dt and

2.5 加载制度

模型受到竖向荷载和水平荷载的同时作用，根据轴压比计算出的竖向荷载换算成均布荷载来模拟试验中的竖向力；水平位移加载采用分级式加载，加载全程共12级，位移加载幅值初级为5、10、15 mm，并由此类推，每增加一级增加 5 mm，最大位移加载到60 mm，每级加载循环两次。具体加载制度如图7所示。

图7 加载制度示意图Fig.7 Schematic diagram of loading system

3 数值试验结果与墙体抗震性能分析

3.1 滞回曲线

四片墙体滞回曲线如图8所示，可知：

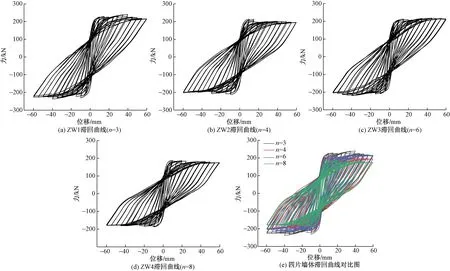
图8 四片墙体滞回曲线Fig.8 Hysteresis curves of shear wall

(1)四片墙体的滞回曲线没有捏缩，不同竖缝形式墙体滞回曲线形状一致，相对饱满，说明装配式竖缝中空剪力墙是耗能较好的墙体。

(2)滞回曲线的饱满程度随墙体比值n的增大而提升；滞回曲线饱满程度越高，说明墙体中钢筋与混凝土协同性越强，墙体耗能能力越好。

3.2 骨架曲线

墙体模型骨架曲线对比如图9所示。加载后期，墙体逐渐屈服，曲线没有明显的峰值点；墙体承载力随比值n的增加而降低，但承载力下降速率缓慢，表明竖缝中空墙体在弹塑性阶段有较强的变形能力。

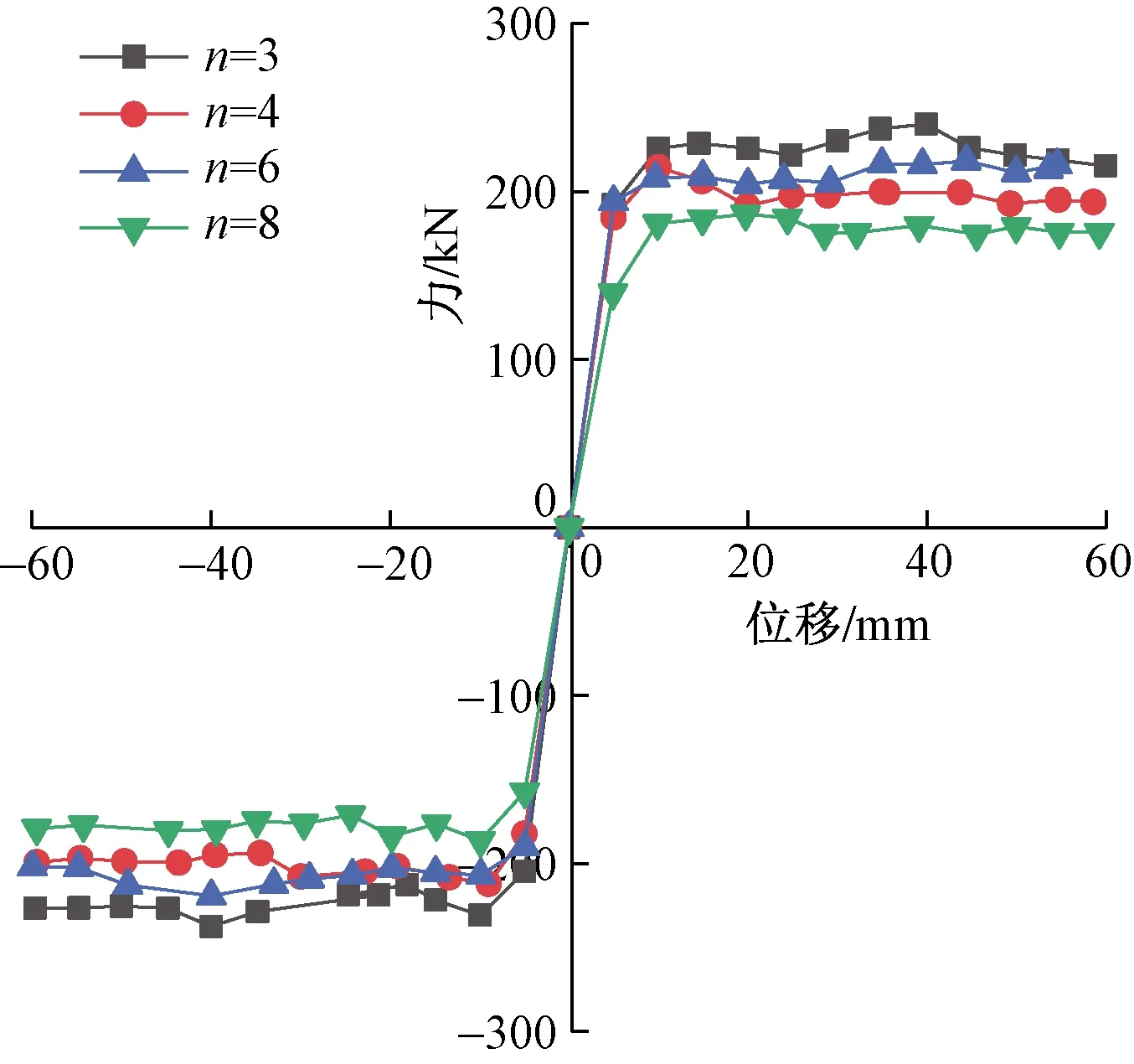
图9 剪力墙骨架曲线Fig.9 Shear wall skeleton curve

3.3 耗能与等效黏滞阻尼系数

耗能能力是评判结构或构件抗震性能的主要指标[11]，用荷载-位移曲线所包围的面积来表示。一般采用等效黏滞阻尼系数(he)对耗能能力进行评定，计算公式为

(4)

等效黏滞阻尼系数计算简图如图10所示，经计算得到的阻尼系数随墙体缝间墙高宽比变化如图11所示。

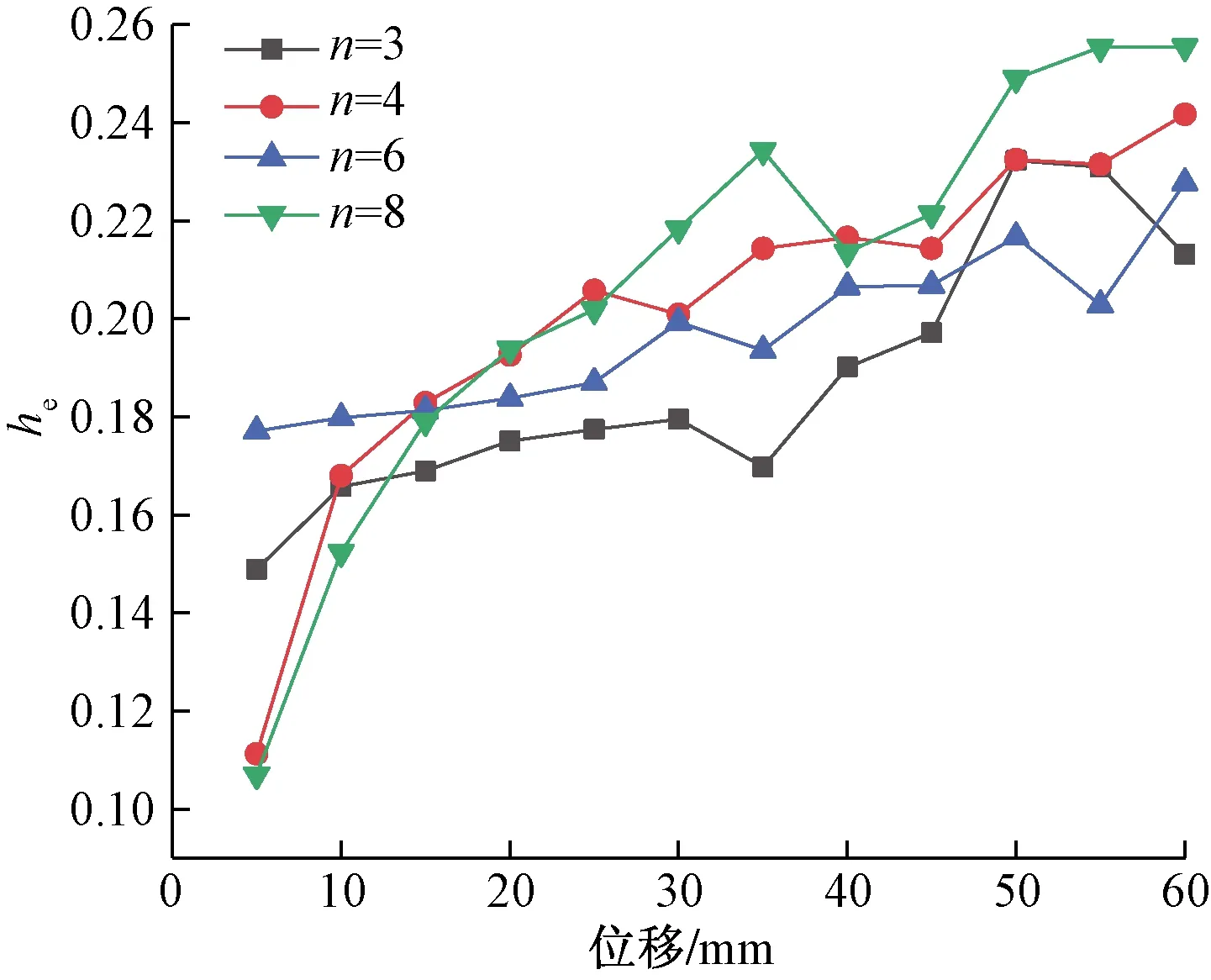
图10 等效黏滞阻尼系数示意图Fig.10 Equivalent viscous damping coefficient

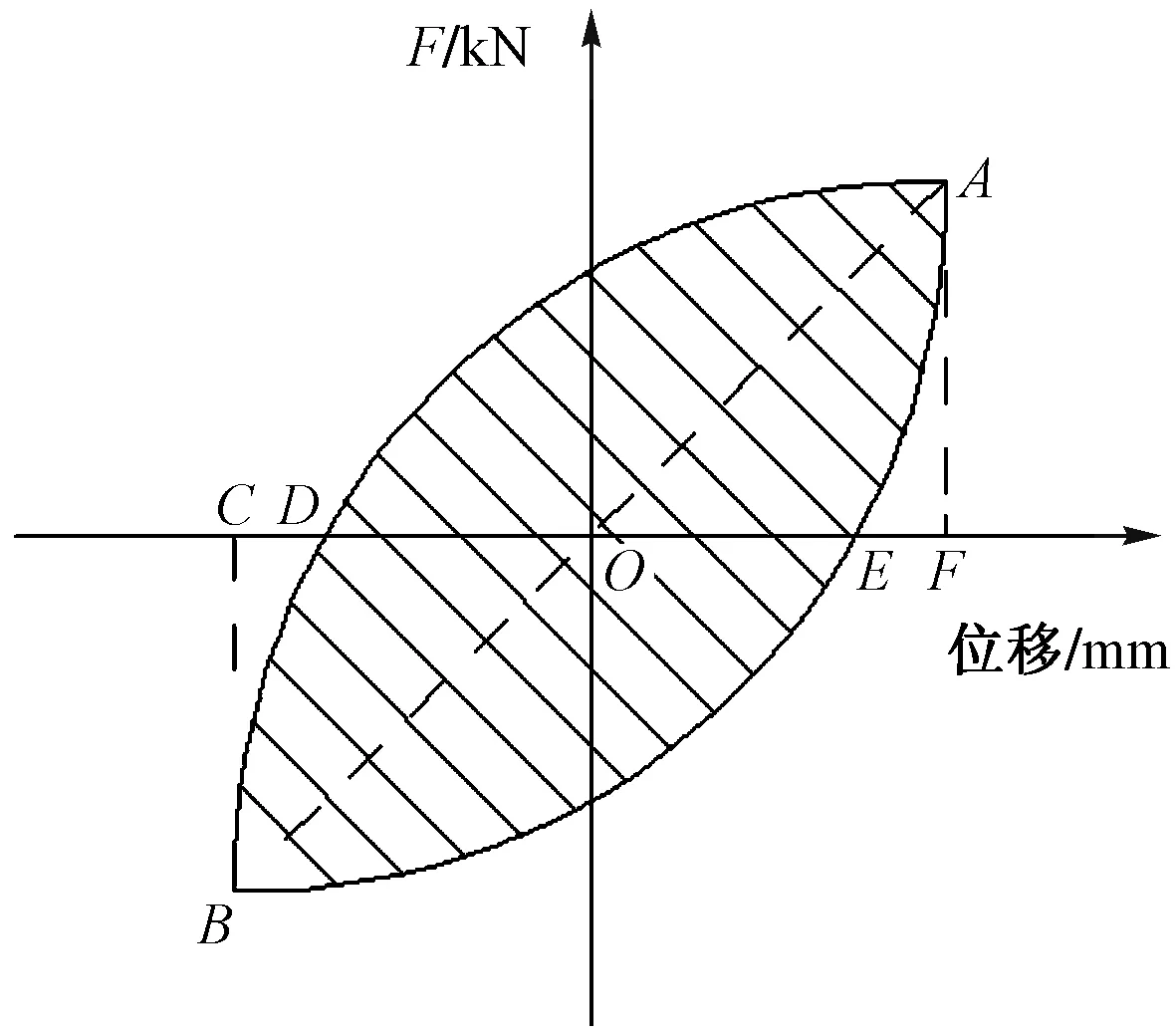
图11 剪力墙等效黏滞阻尼系数Fig.11 Viscous damping coefficient curve of shear wall

通过黏滞性阻尼系数对比图，可知：每片剪力墙的耗能能力都很好，墙体的等效黏滞阻尼系数随缝间墙高宽比(n)的增大而变大，原因是竖缝的设置改变墙体的受力形式，从而改善了墙体的延性；说明缝间墙高宽比通过影响结构的受力形式，进而影响结构的延性，延性越好，耗能能力越强。

3.4 刚度退化

为研究墙体在低周反复加载作用下的刚度退化特性，一般用平均刚度Ki来评定，即

(5)

式(5)中：Pi、Δi分别为第i次加载所达到的最大荷载以及相应的最大位移，四片墙体刚度退化曲线对比如图12所示，可以得出:

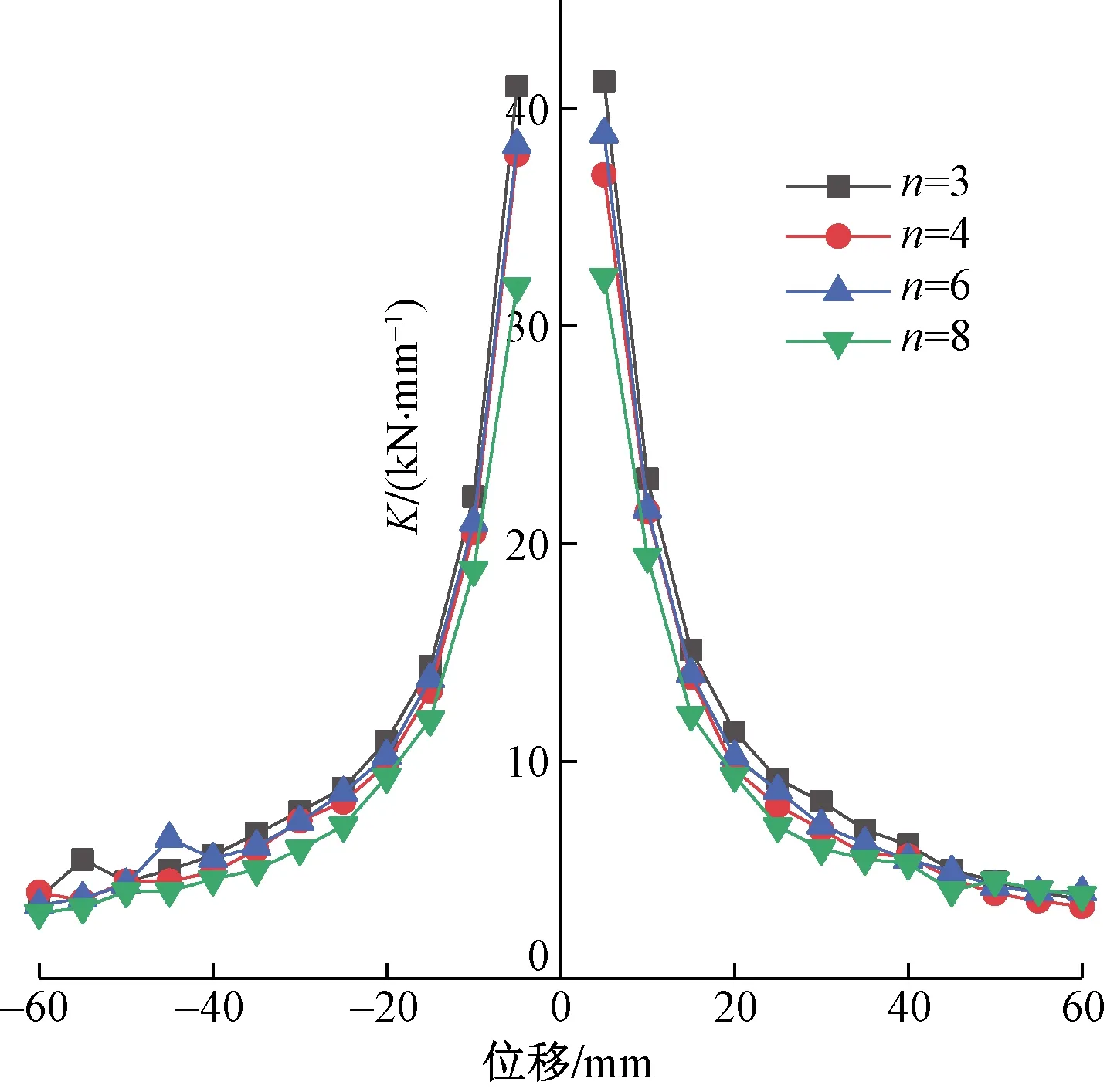
图12 剪力墙刚度退化曲线Fig.12 Stiffness degradation curve of shear wall

(1)加载初期，ZW1初始刚度较大，ZW4初始刚度最小，ZW2与ZW3墙体刚度接近，表明缝间墙高宽比影响墙体的初始刚度。

(2)在加载过程中，ZW1刚度退化最快，ZW4刚度退化最慢，说明缝间墙高宽比越大，刚度退越缓慢。

3.5 墙体的延性性能分析

为研究结构或构件的延性，选取位移延性为指标，具体公式为

(6)

式(6)中：Δu表示极限变形；Δy表示屈服变形。各剪力墙的位移特性以及延性系数如表5所示。

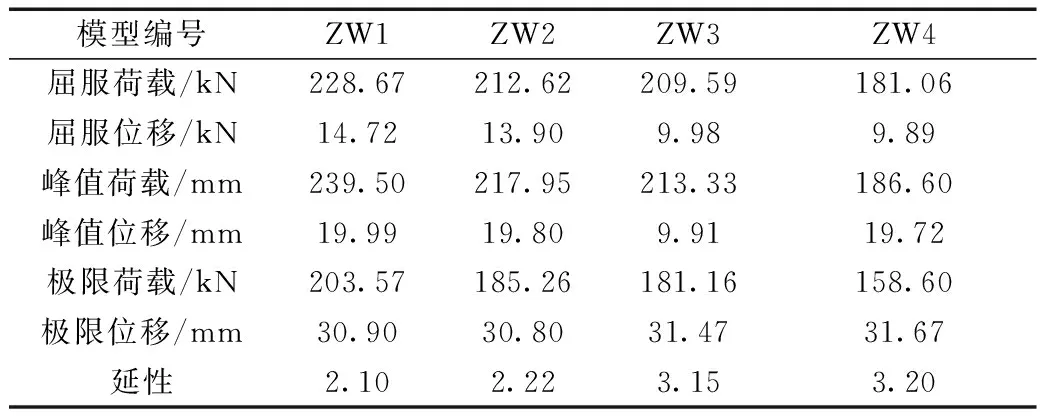
表5 模型特征点参数Table 5 Feature point parameters

分析表5数据得到：①墙体的屈服荷载随墙体比值n的增大而降低；②墙体的延性随着缝间墙的高宽比的增加而增大。说明墙体从明显屈服到极限荷载有较长的发展过程和较好的变形能力，有利于墙体达到“大震不倒”的效果。

4 结论

研究利用数值模拟的方法，研究不同缝间墙高宽比对竖缝中空剪力墙抗震性能的影响，得出以下结论。

(1)缝间墙高宽比影响墙体的耗能能力，即增大缝间墙高宽比，耗能能力提升。

(2)缝间墙高宽比增大，削弱了墙体的刚度，同时减缓了刚度退化速度。

(3)竖缝的设置影响墙体的破坏形态，改善了墙体的延性，提高了墙体的抗震性能。

因此，在保证墙体承载力前提下，选择缝间墙高宽比较大的剪力墙，抗震性能更好。