T700纤维缠绕发动机壳体力学性能分析及优化设计

王 伟， 常新龙， 张有宏， 胡 宽， 王春文

(火箭军工程大学， 西安 710025)

复合材料具有比强度大、比模量大、耐高温、耐腐蚀、易于设计等优良特性，应用广泛[1]。

复合材料具有安全可靠性高、使用寿命长、承压能力大等特点，在航空航天、医疗、新能源汽车等领域的应用前景较为广阔[2-3]。纤维缠绕复合材料发动机壳体采用湿法缠绕成型工艺，材料采用T700/环氧树脂，湿法缠绕是将经过树脂胶液浸渍的连续纤维或布带按一定规律缠绕到芯模上，然后固化、脱模成为复合材料制品的工艺[4]。壳体作为固体火箭发动机的重要组成部分，在工作过程中承受高温、高压的作用。复合材料具有强度高、质量轻的优点，符合发动机壳体设计的需求，在保证发动机壳体的力学性能的同时，有效降低固体火箭发动机的消极质量[5]。纤维缠绕壳体是发动机主要承力结构，研究复合材料壳体的力学性能分析及优化设计在生产制造中是切实可行的，也是必不可少的。

李瑶[6]采用有限元软件对固体火箭发动机壳体建模，利用网格理论分析纤维缠绕壳体的强度，分析不同铺层顺序对强度的影响，并提出最优铺层方式，在满足结构使用需求的情况下对壳体优化设计；Akbari等[7]采用纤维缠绕工艺制品，研究纤维复合材料圆柱壳体的力学性能与屈曲性能；林松等[8]基于网格理论，对发动机壳体强度进行设计，研究制造工艺，结合水压爆破试验验证设计方法的有效性；Asghari等[9]采用有限元软件ANSYS对复合材料壳体刚度矩阵进行计算，并与实验件计算结果数据相关联，研究探讨了碳纤维复合材料壳体的残余应力的发展。

在发动机壳体临界爆破压强下，减少纤维用量，降低成本，减轻发动机壳体质量是解决问题的关键，故现通过有限元优化设计软件首先对纤维缠绕壳体进行力学性能分析，研究容易发生失效部位，为纤维缠绕壳体优化设计提供理论依据；纤维缠绕壳体的优化设计以纤维缠绕层的厚度为设计变量，有限元分析的应力应变结果为约束条件，纤维缠绕壳体质量为优化目标，在满足纤维缠绕壳体临界爆破压强下，对纤维缠绕壳体进行优化设计，并对优化后的壳体基于强度理论进行校核。

1 纤维缠绕固体火箭发动机壳体建模

1.1 纤维缠绕固体火箭发动机壳体基本尺寸计算

复合材料壳体是由纤维缠绕结构、前后裙和前后接头组成的回转壳体，两端为半椭球形状，中部为直筒段[10]。纤维缠绕固体火箭发动机壳体采用T700/环氧树脂材料，材料性能如表1所示。

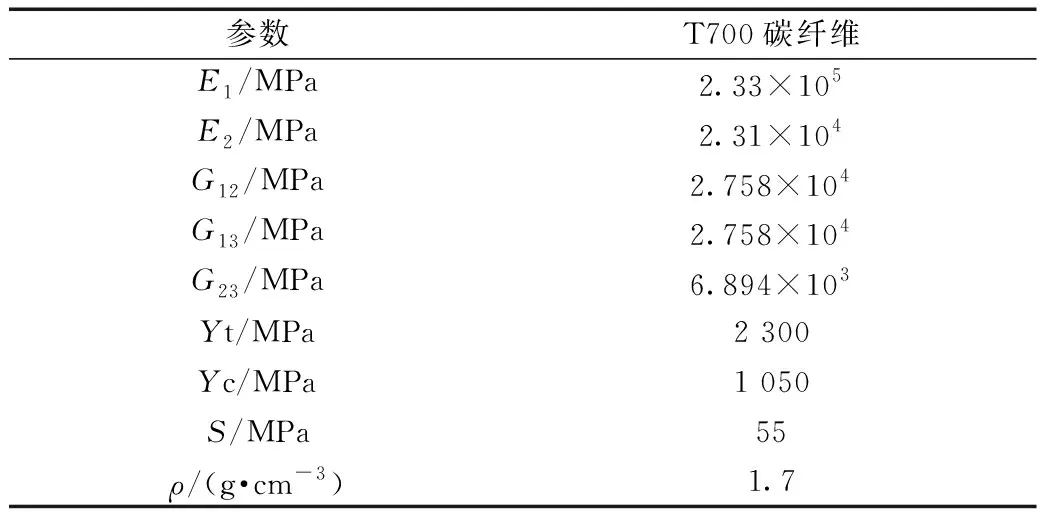
表1 T700碳纤维/环氧树脂材料力学性能Table 1 Mechanical properties of T700 carbon fiber/epoxy resin

纤维缠绕壳体经过湿法缠绕制备而成，壳体封头段椭球比2∶1，纤维缠绕壳体封头段极孔直径为70 mm，直筒段直径为150 mm，直筒段长度为 150 mm，纤维缠绕壳体直筒段纤维缠绕角度为±28°、90°，缠绕顺序为[90°2/±28°2]3，共12层，总厚度约为2.2 mm，由于不同位置复合材料层的厚度与纤维缠绕方向均不相同，因此，建模时需将原本连续的壳体内侧的椭圆线离散成一定的分数[11]。纤维缠绕壳体封头段不同位置纤维缠绕角度计算公式为

(1)

式(1)中：θx为纤维缠绕壳体封头段不同位置的缠绕角度；R0为纤维缠绕壳体极孔半径；Rx为纤维缠绕角度对应的纬度圆半径。当R0=Rx时，纤维缠绕方向与壳体封头段极孔相切，θx=90°，随着壳体封头段纬度圆半径Rx的逐渐减小，θx逐渐增大，并越来越接近于壳体极孔处。

如若将壳体封头段细致划分，计算量相对庞大，过程相对烦琐。为了提高计算效率，并且考虑计算准确性的影响，将纤维缠绕壳体封头段分为8个区域，将式(1)计算的纤维缠绕角度分别对应到8个区域。壳体封头段纤维缠绕角度按区域，自极孔向筒身段方向分别为90°、46.2°、37.3°、32.6°、30.2°、28.4°、27.4°、27.1°，纤维缠绕方式为[90°]6、[±46.2°]3、[±37.3°]3、[±32.6°]3、[±30.2°]3、[±28.4°]3、[±27.4°]3、[±27.1°]3，如图1所示。

图1 纤维缠绕壳体封头段区域角度示意图Fig.1 Angle diagram of head section of filament wound shell

依据网格理论，封头段的厚度随纬度圆的半径而变化，厚度hf方程为

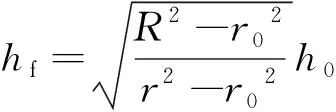
(2)

式(2)中：hf为纤维缠绕壳体不同位置处的厚度；R为纤维缠绕壳体直筒段半径；r为纤维缠绕壳体不同位置处的纬度圆的半径；r0为纤维缠绕壳体封头段极孔半径。根据式(1)、式(2)，计算得出较拟合的纤维缠绕壳体封头段厚度，纤维缠绕固体火箭发动机缩比壳体实物如图2(a)所示，根据纤维缠绕缩比壳体实物尺寸及计算所得纤维缠绕壳体封头段不同位置厚度，构建相应的纤维缠绕壳体有限元模型如图2(b)所示。

图2 纤维缠绕壳体实物与有限元模型Fig.2 Material object and finite element model of filament wound shell

1.2 纤维缠绕固体火箭发动机壳体有限元模型网格划分

对纤维缠绕固体火箭发动机壳体模型简化，认为是对称的3D有限元模型，受力状态与边界约束条件同样具有对称性，所以采用纤维缠绕壳体有限元模型的1/8进行计算，简化仿真计算，提高计算效率，根据上文计算得出的纤维缠绕壳体直筒段与封头段的厚度，建立对应的纤维缠绕壳体1/8有限元模型如图3所示。

图3 纤维缠绕1/8壳体有限元模型示意图Fig.3 Schematic diagram of finite element model of filament wound 1/8 shell

采用Hyper Mesh有限元网格划分软件，首先对纤维缠绕壳体封头段进行网格划分，网格使用四面体单元，在网格划分过程中，纤维缠绕壳体封头段不同位置处厚度不同，纬度圆半径不同，故网格划分不均匀。对网格质量检查，并细分网格，查找重复单元，重新调整网格划分数量，共1 740个单元。

纤维缠绕壳体直筒段与封头段因为形状不同，会导致网格单元发生变化，纤维缠绕壳体封头段接近筒身段区域与纤维缠绕壳体直筒段壳体厚度相近，采用相同大小的有限元网格单元，纤维缠绕壳体直筒段为固体火箭发动机受力主体，具有相同的铺层角度与厚度，采用四面体网格划分，进行网格质量检查，并细化网格，查找重复单元。纤维缠绕1/8壳体模型有限元网格划分最终结果如图4所示。

图4 纤维缠绕1/8壳体有限元模型网格划分示意图Fig.4 Mesh generation of finite element model for filament wound 1/8 shell

纤维缠绕固体火箭发动机壳体有限元模型是对称结构，故施加边界约束也是对称的。纤维缠绕壳体直筒段皆为接触面，故施加固定约束；纤维缠绕壳体封头段两侧为连接面，施加固定约束。

2 纤维缠绕固体火箭发动机壳体力学性能分析

纤维缠绕固体火箭发动机壳体承受35 MPa的压强时，产生的形变量、应力结果如图5、图6所示。

图5 纤维缠绕壳体形变示意图(1∶15)Fig.5 Schematic diagram of filament wound shell shape variation(1∶15)

图6 纤维缠绕壳体应力云图(1∶15)Fig.6 Stress nephogram of filament wound shell(1∶15)

图5所示为纤维缠绕壳体承受内压的形变示意图，从图5可以看出，纤维缠绕壳体发生形变主要集中在封头段极孔附近和直筒段中间部位，产生最大位移为1.436 mm，沿中心轴向方向逐渐减小，但考虑到纤维缠绕壳体封头段极孔处是交界面，存在复合材料与金属材料交界，故该交界面实际情况更容易发生失效。

如图6所示，纤维缠绕壳体承受均匀35 MPa压强时，产生的Von-Mises应力沿轴线逐渐变大，并集中在直筒段，因为在纤维缠绕壳体中，直筒段是主要承载部位，受力最大，较容易发生失效；纤维缠绕壳体封头段产生应力变化较小，但应考虑复合材料与金属材料交界面处同样较容易发生失效。

3 纤维缠绕固体火箭发动机壳体质量优化及强度分析

3.1 纤维缠绕壳体质量优化

结构优化设计是从多个设计方案选择最优的设计方法，以数学理论为基础，根据结构设计需要满足的性能指标，设定约束条件，选择设计优化变量，建立目标函数，寻找最优解。

利用有限元优化设计软件Hyper Works中OptiStruct尺寸优化功能对纤维缠绕壳体进行质量优化。OptiStruct是一款以有限元为基础的优化设计软件，优化功能强大，主要包括拓扑优化、形貌优化、尺寸优化、铺层顺序优化等。尺寸优化是在具有一定模型设计思路后对结构件进行详细的设计，通过改变单元的属性完成设计目标。以纤维缠绕壳体质量最小化为设计目标，有限元分析的应变结果为约束条件，小于有限元分析产生的最大应变，以纤维缠绕铺层厚度为设计变量，对纤维缠绕固体火箭发动机壳体进行质量优化。

设计要求在满足使用需求的前提下，减少壳体质量，减少纤维用量，降低成本，采用与上文有限元分析相同的纤维缠绕模型，以纤维铺层厚度为设计变量，依据计算得出的纤维层铺层厚度，封头段网格自上而下纤维缠绕厚度tf取值范围分别为[6.00 mm，6.33 mm]、[4.20 mm，4.54 mm]、[3.00 mm，3.33 mm]、[2.50 mm，2.82 mm]、[2.20 mm，2.54 mm]、[2.20 mm，2.37 mm]、[2.20 mm，2.27 mm]、[2.20 mm，2.22 mm]，直筒段纤维缠绕层铺层厚度取值范围为[1.8 mm，2.4 mm]。

纤维缠绕壳体承受35 MPa的压强时，位移最大为1.436 mm，故纤维缠绕壳体优化的约束条件为小于内压力产生的最大位移，要求优化后的壳体满足设计使用需求，优化纤维缠绕层的厚度，寻找最优结果，优化结果如图7所示。

如图7所示，优化后的纤维壳体缠绕层厚度直筒段厚度为1.8 mm，共12层，单层缠绕厚度为 0.15 mm，纤维缠绕壳体封头段厚度最大厚度为 6 mm，最小厚度为2.26 mm，纤维缠绕壳体优化前后的厚度变化如图8所示。

图7 纤维缠绕壳体厚度优化示意图(1∶15)Fig.7 Schematic diagram of thickness optimization of filament wound shell(1∶15)

图8 纤维缠绕壳体厚度优化变化量示意图(1∶15)Fig.8 Schematic diagram of optimized variation of filament wound shell thickness(1∶15)

如图8所示，纤维缠绕壳体厚度在直筒段与封头段连接处变化较小，因为在纤维缠绕壳体直筒段与封头段处，存在形状突变，失效较为容易产生，所以需要纤维缠绕壳体交界处过渡相对平滑，保证满足设计使用需求；纤维缠绕壳体直筒段厚度变化最大，优化后的结果满足约束条件，故优化结果满足设计使用需求。质量最小化优化结果主要集中在纤维缠绕壳体直筒段，纤维缠绕壳体封头段厚度变化较小。

3.2 优化后纤维缠绕壳体强度校核

采用优化后的纤维缠绕壳体厚度，建立有限元模型，施加相同的边界条件，对纤维缠绕壳体均匀施加35 MPa压强，同样采用1/8纤维缠绕壳体进行分析计算，提高运算效率。引入强度比概念，即：许用值/计算值，许用值即纤维缠绕壳体材料的临界强度，许用值即施加的35 MPa均匀内压，分析结果如图9所示。

图9 纤维缠绕壳体强度校核示意图(1∶15)Fig.9 Schematic diagram for strength check of filament wound shell(1∶15)

如图9所示，优化后的纤维缠绕发动机壳体封头段强度比均大于1，表明壳体许用值大于计算值，且在封头段与直筒段交界处，强度最高，不容易发生破坏；直筒段的厚度中心处，强度最大，不容易发生破坏，沿中心轴向逐渐减小，最小值接近1，即施加均匀载荷已经达到纤维缠绕壳体临界爆破压强。优化后的纤维缠绕壳体强度校核示意图与壳体承受均匀压强时，产生的位移、应力图相似，均沿中心轴向，更容易发生失效，验证了对纤维缠绕壳体力学性能分析的正确性。优化结果表明：优化后的壳体满足强度设计使用需求，优化方法是真实可靠的。

4 结论

采用有限元优化设计软件对纤维缠绕固体火箭发动机壳体进行力学性能分析及质量优化，分析纤维缠绕壳体承受内压时产生的应力应变结果；利用尺寸优化功能，优化纤维缠绕固体火箭发动机壳体质量，并对优化后的结果进行强度分析，得到以下结论。

(1)纤维缠绕复合材料壳体经过优化后，壳体质量减轻12.09%，优化结果满足约束条件，是可行的设计。

(2)引入强度比概念，对优化后的壳体进行强度校核，结果表明：优化后的壳体满足壳体材料强度，优化的方法是切实可行的，这也为纤维缠绕壳体的生产实践提供了理论基础。