基于非线性PID的连续搅拌反应釜控制方法

范 政, 赵 虹

(桂林理工大学机械与控制工程学院, 桂林 541006)

比例-积分-微分(proportion integration differentiation, PID)控制算法是过程控制系统中普遍运用的算法，在化工、冶金、机械等领域得到了广泛的运用。随着控制理论的不断发展，各种新型的控制方法层出不穷，但是PID控制算法拥有结构简单、鲁棒性强等特点，仍然是控制领域运用最多的算法之一。但是PID控制算法参数固定不变，因此，人们利用非线性函数对传统PID控制器进行改进，使控制器的控制性能和鲁棒性提高[1]，以达到提高系统控制性能的目的，研究和运用越来越广泛。

非线性PID(nonlinear PID, NPID)控制器的形式可以根据特定的系统控制要求进行构造。韩京清等[2]提出一种非线性跟踪-微分器的控制方法，在运动控制系统中得到运用。Lee等[3]用一种基于误差的非线性函数构造NPID控制器，与传统线性PID相比控制性能更好。李明哲[4]在结构振动控制中运用NPID控制器，通过仿真实验证明了该方法相比线性二次型调节器控制更灵活。晏东[5]使用一种基于修正的非线性函数的NPID控制方法对永磁直线同步电机控制进行控制，相比传统PID控制，响应速度更快，位置动态跟踪误差更小。阮晓钢等[6]针对一种可以在二维平面全向移动的球形轮移动机器人系统，提出一种双闭环NPID控制策略，仿真结果证明了所提控制策略相比传统PID控制算法稳定性更强。Najm等[7]针对六自由度四旋翼无人机控制系统的平移和旋转运动，提出一种NPID控制器，运用于滚转、俯仰、偏航、高度和位置子系统，仿真结果表明NPID控制系统在跟踪速度、动态性能和稳态性能上比线性PID更优。

连续搅拌反应釜(continuously stirred tank reactor, CSTR)是化工生产的主要设备之一，可以用于原料发酵、微生物、化学原料的充分混合及油漆、制药、试剂、合成材料等工业生产中。CSTR对象存在非线性、不稳定性和参数不确定性[8]，线性PID控制难以满足系统控制需求。因此，现将一类NPID控制器运用于CSTR控制系统中，以改善线性PID算法的控制效果，提高控制性能。

1 CSTR过程模型

以一个CSTR为研究对象，系统存在强非线性，CSTR化学反应是不可逆转的放热反应。CSTR的结构图如图1所示[9]。

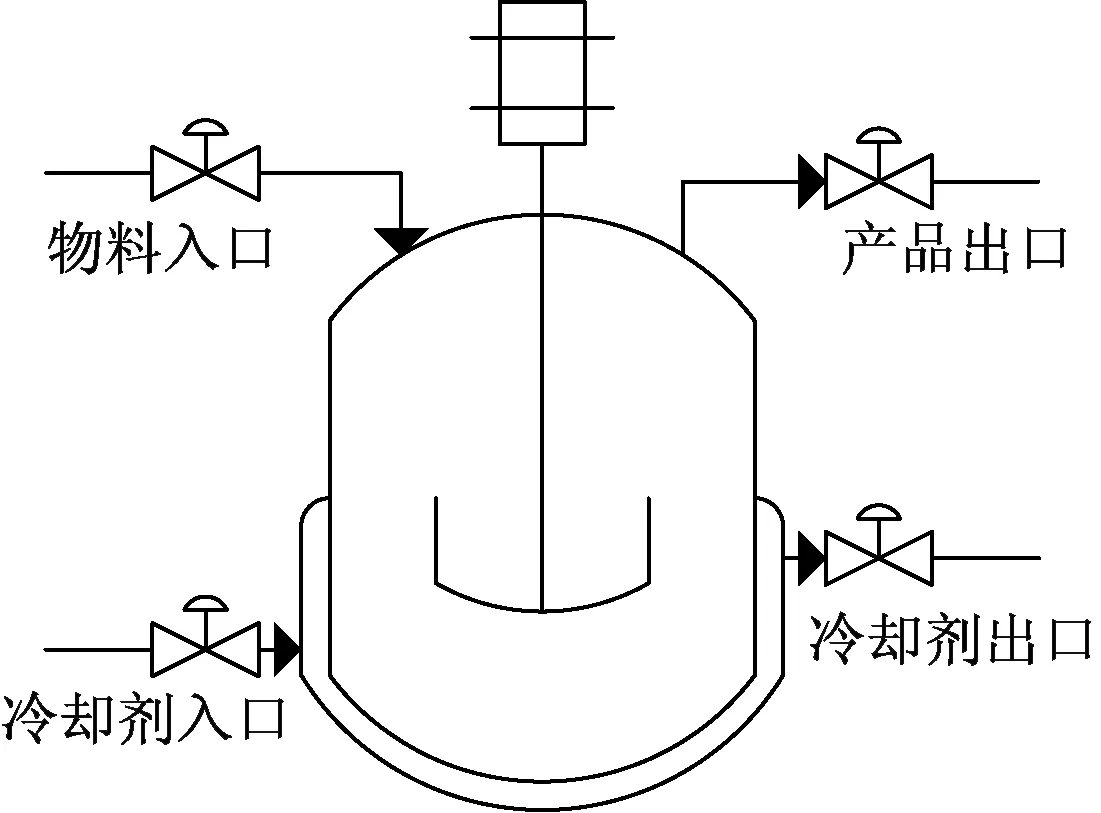
图1 CSTR结构图Fig.1 CSTR structure diagram

从图1可知，反应物料进入CSTR容器中，在内部发生不可逆放热反应后，得到产品，反应过程为强放热过程，需要向冷却夹套内通入冷却剂，通过控制冷却剂的流量来控制反应釜内温度，使其恒定在一定范围内。

不考虑冷却剂温度，根据冷却剂温度与CSTR出料温度的关系，建立对象的数学模型[9]为

(1)

(2)

式中：UA为传热系数；S为传热面积；其他各个变量所表示的含义及参数的具体数值[9]如表1所示。

表1 CSTR各参数取值Table 1 Each parameter of CSTR

续表1

(3)

(4)

2 NPID控制算法描述

PID控制器以系统设定值与实际值之间的偏差e(t)作为控制器输入信号，通过调节控制器的比例系数kp、积分时间Ti、微分时间Td三个参数，以满足系统的控制要求。PID控制系统框图如图2所示，控制器的控制规律数学表达式为

图2 PID控制系统框图Fig.2 PID control system diagram

(5)

采用PI控制器对CSTR出料温度进行控制，以4∶1衰减比整定CSTR出料温度控制曲线，得到图3所示的出料温度响应曲线。

图3 CSTR出料温度响应曲线Fig.3 Response curve of CSTR discharge temperature

从CSTR出料温度的响应曲线可知，采用PI控制器控制CSTR出料温度时，温度曲线超调量过大，调节时间长，通过分析误差与PID参数的关系，从初始段到第一个波谷，系统误差e(t)经历先减小后增加的过程。在系统误差逐渐减小的过程中，为了使CSTR温度超调量减小，要求比例增益系数Kp随误差变化经历先逐渐减小后逐渐增大的过程，积分增益系数Ki随误差变化的过程为先增大后减小。同理，在第一个波谷到第一个波峰阶段，系统误差同样经历由大变小，而后由小变大的过程，要求比例增益系数Kp随误差变化经历先逐渐减小后逐渐增大的过程，积分增益系数Ki随误差变化的过程为先增大后减小。在控制系统的调节过程中，为达到减小超调量的目的，微分增益系数Kd应在系统误差逐渐减小的过程中，增大微分增益系数Kd，误差逐渐增大时，减小微分增益系数Kd，且要求微分增益系数Kd的变化幅度不宜过大，避免系统抗干扰能力变差。根据上述分析，可以将NPID控制器在CSTR温度控制过程中参数Kp、Ki、Kd随误差变化的曲线总结为图4，其中比例增益系数Kp、积分增益系数Ki、微分增益系数Kd的变化规律[11]为

图4 NPID控制器参数Kp、Ki、Kd随误差变化的曲线Fig.4 Parameters of Kp, Ki and Kd of NPID controller curves varying with error

Kp[e(t)]=ap+bp{1-sech[cpe(t)]}

(6)

Ki[e(t)]=aisech[bie(t)]

(7)

Kd[e(t),e(v)]=ad+bd/{1+cdexp[dde(t)]}

(8)

式中：ap、bp、cp、ai、bi、ad、bd、cd、dd为常数，分别用于调整NPID控制器的参数变化范围和变化速率。

通过上述NPID比例、积分、微分增益系数的描述，以及线性PID控制规律的数学表达式，可以得到NPID控制器的控制规律表达式为

(9)

3 仿真分析

以一个具有强非线性的CSTR对象为研究对象，文献[10]给出了CSTR需要满足的约束条件，其中，反应釜温度T变化范围[400,460] K、出料浓度CA变化范围[0,1] mol/L、冷却剂流量qc的变化范围为[0,130] L/min，在正常工作条件下，系统达到平衡时出料浓度0.1 mol/L，出料温度438.54 K，冷却剂流量为103.41 L/min，对象的数学模型如式(3)、式(4)所示，用于验证NPID控制器在CSTR闭环反馈控制系统的控制性能。根据前人的研究结果，式中各参数的取值为a=1.0，β=0.3，γ=20.0，b=-8.0，Da=0.072。CSTR出料温度控制系统的Simulink仿真图如图5所示。其中NPID控制器的Simulink仿真结构图如图6所示，NPID模块Simulink结构图如图7所示，CSTR对象的Simulink仿真模型如图8所示。

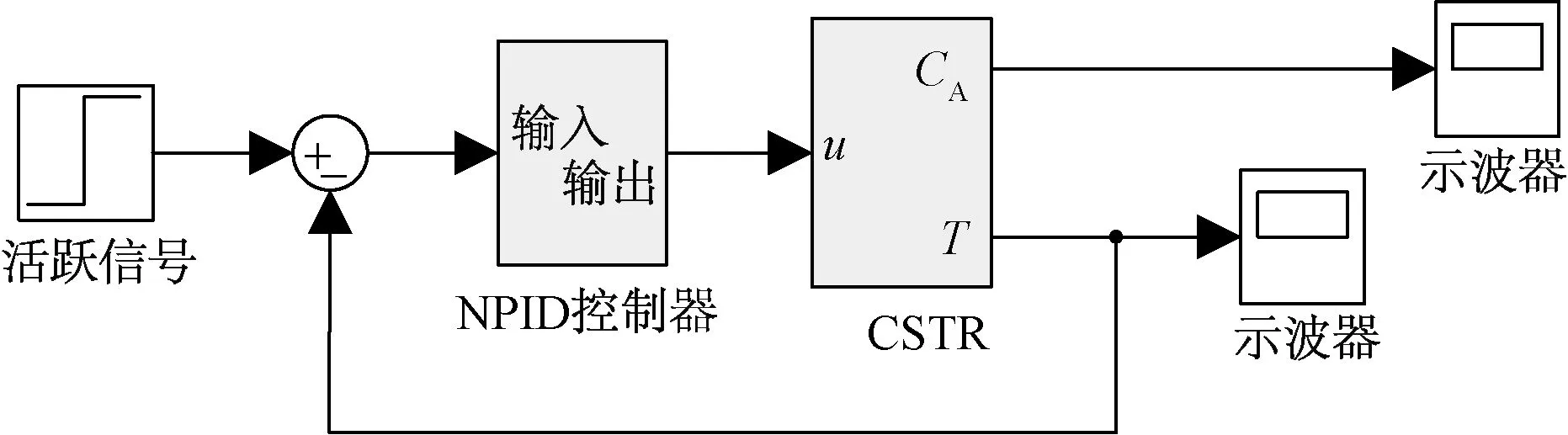
图5 CSTR出料温度控制系统的Simulink仿真图Fig.5 Simulink simulation diagram of CSTR discharge temperature control system

图6 NPID控制器的Simulink仿真结构图Fig.6 Simulink simulation structure chart of nonlinear PID

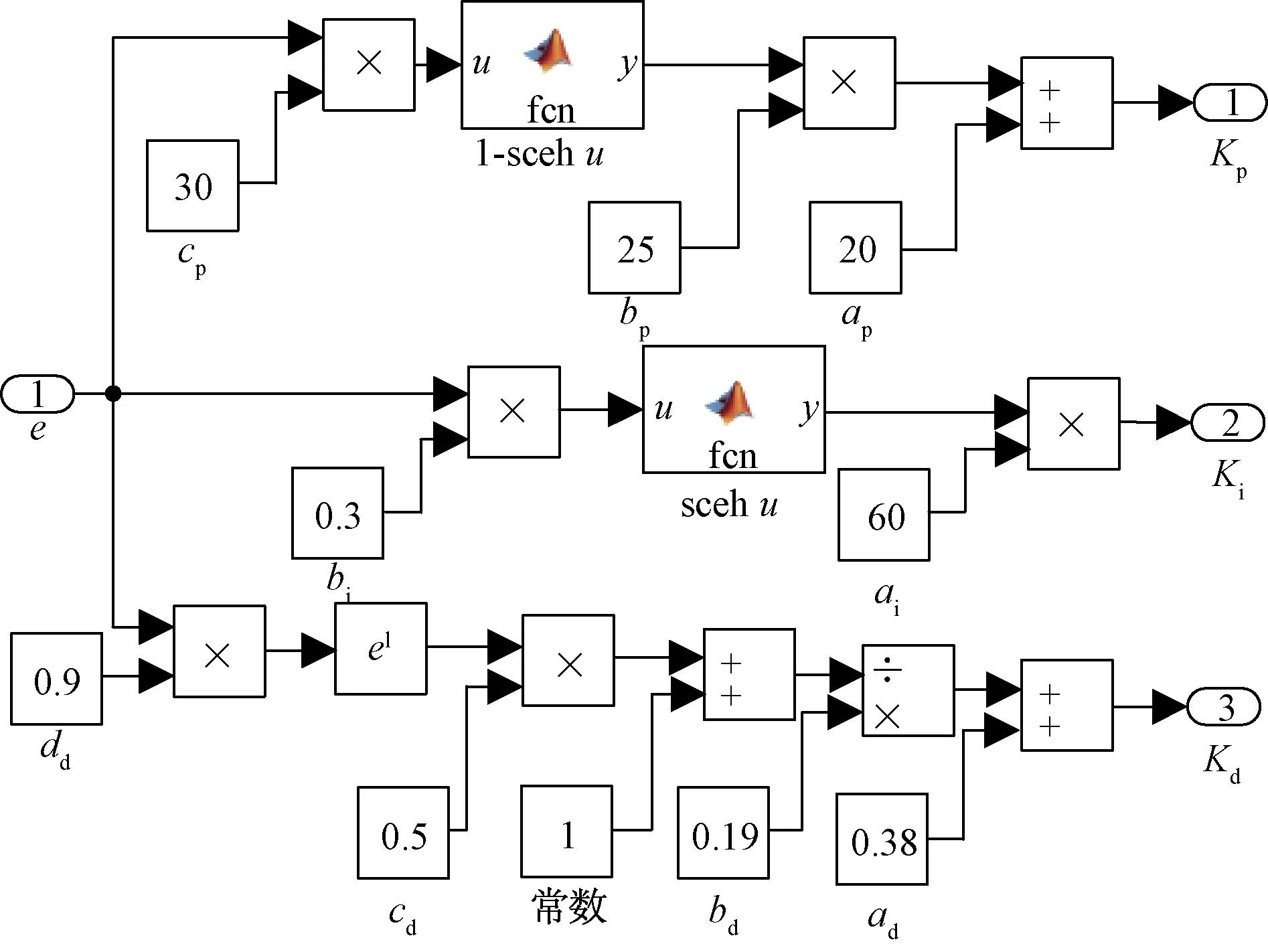
图7 NPID模块Simulink结构图Fig.7 Simulink diagram of NPID module

图8 CSTR对象的Simulink仿真模型Fig.8 Simulink simulation model of CSTR object

3.1 基于NPID控制的CSTR阶跃响应

为了验证NPID控制器的控制性能，以阶跃信号作为系统设定值，通过不断调整控制器的参数，得到理想的响应曲线，并与线性PID控制下，CSTR系统的响应曲线进行比较。给CSTR分别施加幅值为1和1.5的阶跃信号，根据多次反复试凑，得到线性PID控制器的各个参数取值为Kp=10，Ti=15,Td=0.5，NPID控制的各个参数取值为ap=20，bp=25，cp=30，ai=60，bi=0.3，ad=0.388，bd=0.192，cd=0.5，dd=0.9。图9和图10分别表示两类控制器在不同幅值的阶跃信号输入下系统的响应曲线。

图9 CSTR系统的阶跃响应曲线(幅值为1)Fig.9 Step response curve of CSTR system(amplitude 1)

图10 CSTR系统的阶跃响应曲线(幅值为1.5)Fig.10 Step response curve of CSTR system(amplitude 1.5)

从系统的响应曲线可得，系统在幅值为1和1.5的阶跃信号输入下，两种算法控制下系统最终都能回到稳定状态，系统稳态误差为0。为了更加直观地展示两种方法的控制效果，以系统动态性能指标(包括上升时间tr、峰值时间tp、调节时间ts、超调量σ)和时间乘以误差绝对值积分(ITAE)性能指标作为观测量。系统阶跃响应下出料温度响应曲线对应性能指标如表2、表3所示。

表2 CSTR出料温度阶跃响应性能指标(幅值为1)Table 2 Step response performance index of CSTR discharge temperature(amplitude 1)

表3 CSTR出料温度阶跃响应性能指标(幅值为1.5)Table 3 Step response performance index of CSTR discharge temperature(amplitude 1.5)

从表2、表3、图9和图10可知，NPID算法的控制效果更好，系统调节时间更短，出料温度和出料浓度曲线更加平滑，大大改善了系统的动态性能，系统运行更加稳定、高效、快速。

3.2 抗干扰分析

在实际生产中，往往存在众多不可预测的干扰，对控制系统的设计必须考虑系统的抗干扰能力。系统阶跃响应曲线进入稳定状态后，在仿真时间为5、9 s时，对NPID控制系统和线性PID控制系统分别系统施加幅值为1和-1.5的扰动，系统响应曲线如图11所示。对比两种控制方法的响应曲线可知，两种方法在扰动作用下最终都能使系统重新回到稳定状态，且系统稳态误差为0，但是幅值为-1.5的扰动下，线性PID控制CSTR的出料浓度响应曲线出现超调。NPID控制器的抗干扰能力明显强于线性PID控制器，NPID控制算法使得扰动作用下CSTR的出料温度及出料浓度的过渡曲线更加平滑，调节时间更短。

图11 扰动作用下CSTR系统响应曲线Fig.11 Response curve of CSTR system under disturbance

3.3 鲁棒性分析

在化工生产过程中，CSTR内部发生复杂的化学反应。在生产过程中，各个操作过程不同和设备老化等因素影响，可能会引起CSTR系统的参数发生变化，因此CSTR系统是一个时变系统。为了验证NPID控制算法在CSTR系统中的鲁棒性，选取对系统影响较大的Da、b、β作为参数摄动的变量，将3个参数分别变化20%和40%，即Da=0.072→0.086 4、b=-8→-9.6、β=0.3→0.24和Da=0.072→0.100 8、b=-8→-11.2、β=0.3→0.18。CSTR系统在幅值为1的阶跃信号输入下，得到的系统的出料温度和出料浓度响应曲线如图12、图13所示。参数摄动20%和40%时，系统阶跃响应对应的出料温度响应曲线性能指标如表4、表5所示。

表4 参数摄动20%时CSTR出料温度响应曲线性能指标Table 4 Performance index of CSTR discharge temperature response curve with parameter perturbation of 20%

表5 参数摄动40%时CSTR出料温度响应曲线性能指标Table 5 Performance index of CSTR discharge temperature response curve with parameter perturbation of 40%

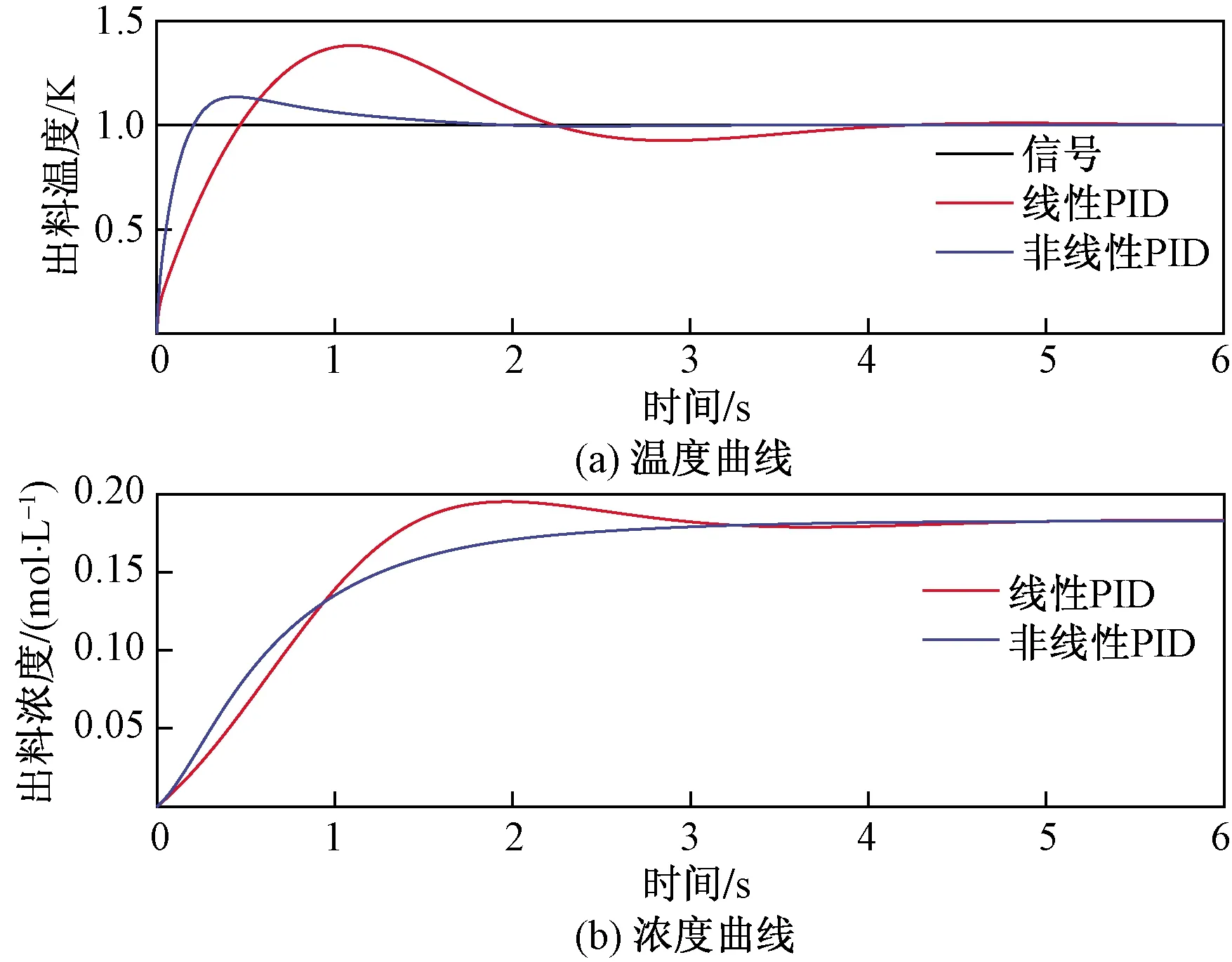
图12 参数摄动20%时CSTR出料温度和浓度响应曲线Fig.12 Response curve of CSTR discharge temperature and concentration with parameter perturbation of 20%

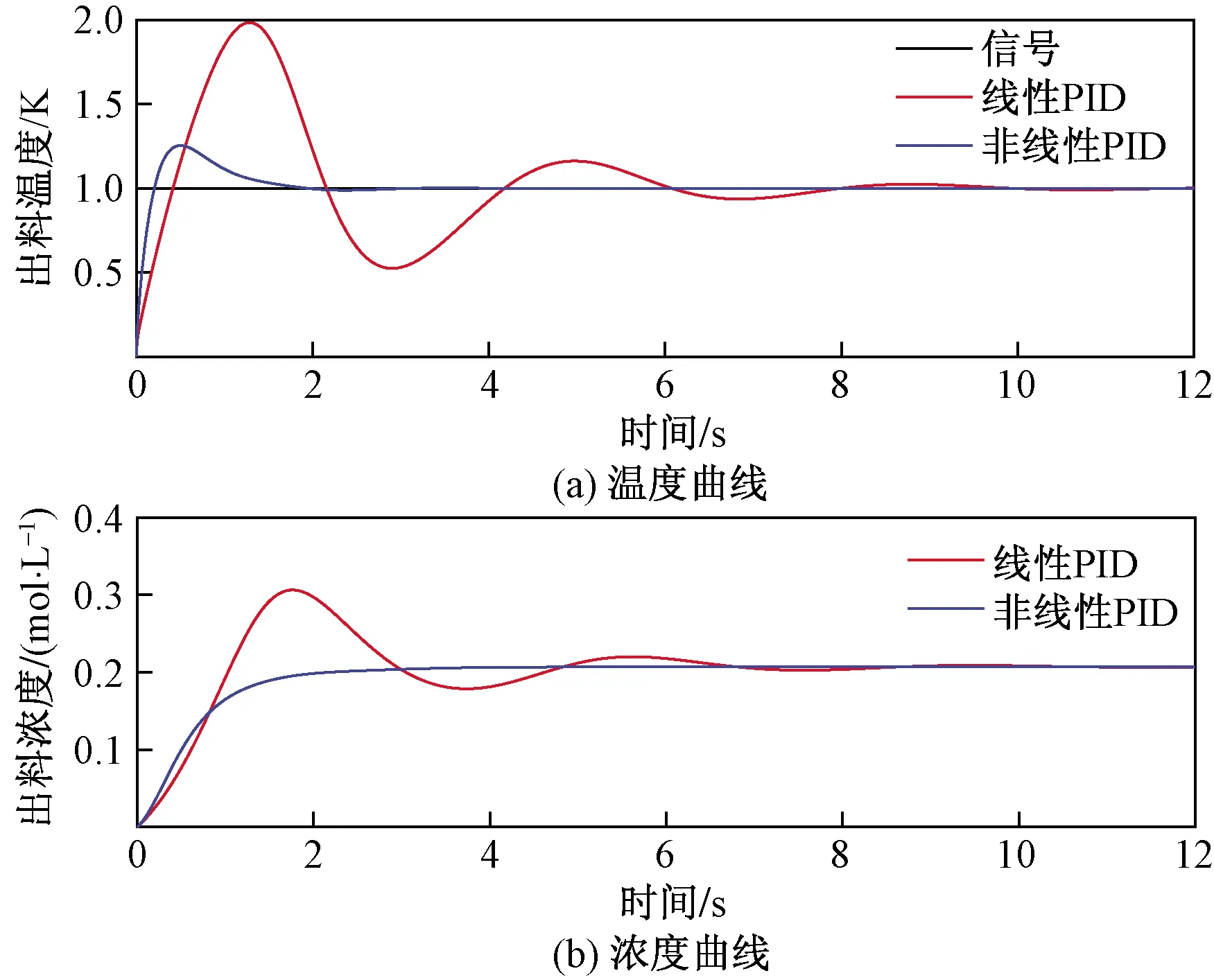
图13 参数摄动40%时CSTR出料温度和浓度响应曲线Fig.13 Response curve of CSTR discharge temperature and concentration with parameter perturbation of 40%

从表4、表5、图12和图13可知，参数摄动20%时，线性PID控制和NPID控制的出料温度响应曲线上升时间tr和峰值时间tp相比原参数曲线变化不大，调节时间ts变化分别为1.31→1.55和2.21→3.83，变化幅度分别为18.3%和73.3%，超调量变化分别为7.9→13.6和18.5→38.3，变化幅度分别为72.2%和107%，ITAE性能指标变化分别为0.05→0.096和0.32→0.85，变化幅度分别为92%和165.6%，NPID控制的出料浓度响应曲线过渡平稳，而线性PID控制的出料浓度响应曲线出现超调。参数摄动40%时，线性PID控制和NPID控制的出料温度响应曲线上升时间tr相比原参数曲线变化不大，峰值时间tp调变化分别为0.43→0.51和1.07→1.27，变化幅度都为18.6%，调节时间ts变化分别为1.31→1.64和2.21→9.15，变化幅度分别为25.2%和314%，超调量变化分别为7.9→25.4和18.5→98.4，变化幅度分别为221.5%和431.9%，ITAE性能指标变化分别为0.05→0.17和0.32→5.05，变化幅度分别为240%和1 478%，NPID控制的出料浓度过渡过程曲线依然平稳，而线性PID控制的出料浓度响应曲线震荡严重，不利于化工生产正常进行。从系统的响应曲线和定量分析数据可知，CSTR系统中，NPID控制算法的鲁棒性比线性PID控制算法更优。

4 结论

以一类CSTR为研究对象，进行了仿真研究。对象具有高度的非线性、不稳定性和参数不确定性，线性PID控制算法不能满足CSTR系统的控制需求。为了提高CSTR系统的控制品质，设计了一种能够根据响应曲线误差变化实时调整PID参数的NPID控制算法。在阶跃信号输入、系统存在扰动、系统在运行过程中参数摄动变化三种情况下，对NPID和线性PID控制算法进行对比仿真研究。实验结果表明，NPID控制算法的控制效果更好，在扰动和参数摄动的情况下，CSTR的出料温度和出料浓度曲线变化更平滑，系统的抗干扰能力和鲁棒性更强。