平茬周期对沙柳林地土壤孔隙结构分形特征的影响

王 凯， 裴志永*， 王文明， 郝少荣， 庞国辉

(1.内蒙古农业大学能源与交通工程学院， 呼和浩特 010018； 2.鄂尔多斯市乌审旗林业局， 鄂尔多斯 017300)

毛乌素沙地是中国风沙治理并取得显著成效的重点区域之一[1]。沙柳作为当地防风固沙的先锋种[2]，其大面积种植有效地改善了林地土壤质地，并且对当地治沙防沙、土壤修复有着重要意义[3]。分形理论已被应用于土壤科学中，并为研究土壤科学提供了新思路。通过分形分析，可以实现对更加复杂空间尺度上土壤结构的定量表达，并能反映植被类型对土壤质地的影响[4]。当前对毛乌素沙地土壤分形维数的研究主要集中于土壤颗粒质量分形维数[5]和体积分形维数[4]，对不同平茬周期(stumping period，SP)下的土壤孔隙结构分形特征的研究较少。沙柳平茬周期的不同会导致林地土壤水、肥、热等条件不同，同时枯落物回归的量也不同。长此以往会对土壤结构的稳定性产生一定的影响。

针对土壤表面分形维数的研究方法主要有压汞法、热力学方法、气体吸附法等。王升福等[6]对人工冻融软黏土采取压汞法研究其孔体积分布分形特征和孔表面积分布分析特征，为研究其孔隙特征提供了新途径。胡康博等[7]同时利用FHH模型法和热力学方法得出河渠泥沙沉积物表面的分形特征。Pfeifer等[8]首次采用吸附法研究了多孔介质的孔隙结构和分形特征。氮气吸附法主要测定的是孔径小于100 nm的孔隙，在研究微孔和中孔时较有优势[9]，气体吸附曲线已经被广泛用于计算多孔材料的分形维数[10]。

现以不同平茬周期的人工沙柳林地的土壤为研究对象，基于氮气吸附法测得不同平茬周期的沙柳林地土壤的试验数据，采用FHH(Frenkel-Halsey-Hill)模型计算分形维数，对林地土壤孔隙结构进行定量描述，分析分形维数与不同平茬周期的人工沙柳林地土壤孔比表面积、总孔体积和平均孔径之间的相关关系，阐明林地土壤孔隙结构的分形特征。以期为该地区的沙柳林地土壤演化规律及营林决策等研究提供理论依据。

1 样品采集和试验方法

1.1 研究区概况

研究地点为地处毛乌素沙地腹部的乌审旗乌兰陶勒盖国有林场。地理位置109°12′E，38°52′N。属温带半干旱半荒漠性气候，年平均气温 7.5 ℃,年温差 30 ℃,年平均风速3.4 m/s，全年风向以西北风为主，年风沙日数 100～252 d，多集中在3—5月。平均降水量300 mm，年平均蒸发量2 100 mm，干燥度 1.9。土壤以栗钙土为主。毛乌素沙地生态系统以灌木为主,主要天然灌木种有：沙柳(Salixpsammophila)、沙蒿(Artemisiasphaerocephala)、柠条锦鸡儿(Caraganakorshinskii)和沙棘(Hippophaerhamnoides)等[11-12]。

1.2 样品采集

试验于2019年6月中旬开展，选取三个相同营造时间(1987年)的丘间低地沙柳林试验区，如图1所示，试验区间距为200～300 m。3个试验区内的沙柳林被当地林业部门按平茬周期为3、5、7 a进行长期抚育，配置形式为一行一带式，呈西南-东北走向，林带间距为3 m,株间距为2 m，在3个试验区内选取长势良好、均匀的沙柳林作为试验样地，大小为20 m×30 m,并调查和采集样地内沙柳林的平均株高、冠幅、叶面积指数等参数，如表1所示。取土样方设置在相邻的沙柳林带之间，大小为1 m×1.5 m，对样方内的土壤进行剖面分层取土。由于研究区的地下水位较高，且沙柳主要吸水根系分布在30 cm左右，故取土深度设置为0～50 cm，取样间隔为10 cm，即0～10、10～20、20～30、30～40、40～50 cm，分别用直径和高均是5 cm、体积为100 cm3环刀分层取土，按五点取样法每层取5个重复土样，将其带回实验室充分混合均匀，最后取适量土壤样品进行氮气吸附试验。

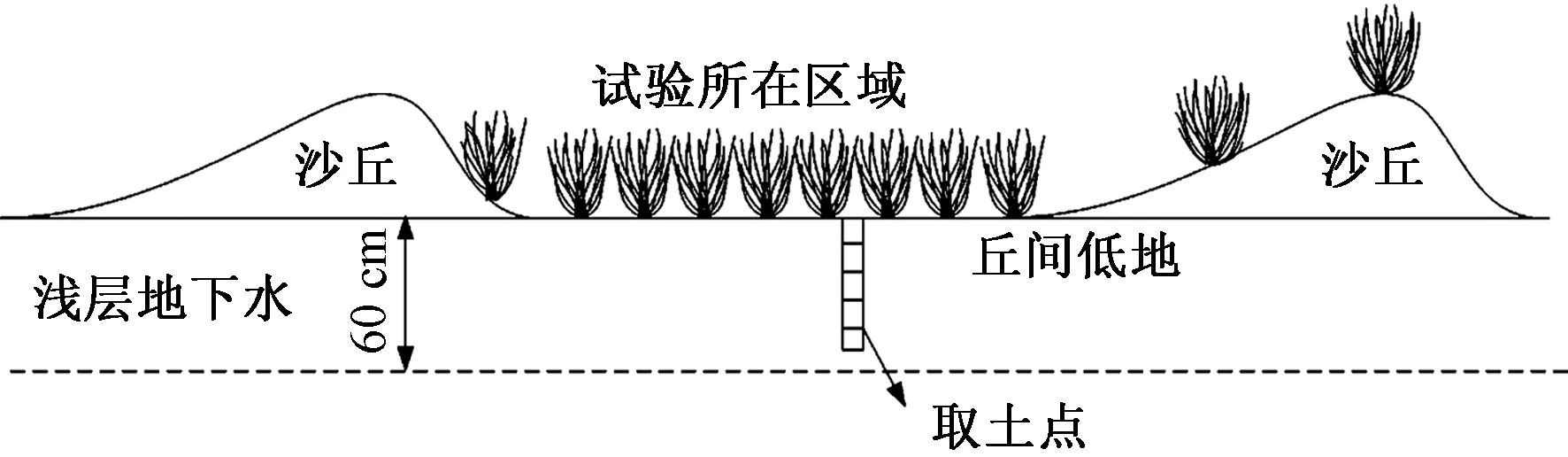
图1 样地所在区域Fig.1 Area of the sample

表1 毛乌素沙地人工沙柳木林试验样地基本特征Table 1 Basic characteristics of test plots of artificial sallow forest in Mu Us Sandy Land

1.3 试验方法

氮气吸附试验采用美国Micromeritics公司生产的Gemini Ⅶ 2390型比表面积测试仪,如图2所示。试验前需要将脱气台温度调至300 ℃ 去除样品中的水分和杂质，并打开和脱气台连接好的氦气瓶及氮气瓶的减压阀对样品进行4 h的脱气处理。采用容量法在室温下以高纯度氮气(大于99.99%)液氮为吸附质，以相对压力(范围为0.01～1 MPa)为横坐标，单位样品质量的氮气吸附量为纵坐标，绘制得到土壤样品的吸附等温线。比表面积的获得根据BET[13]多分子层吸附理论得到，孔径和孔隙体积分布根据BJH理论[14]和 Kelvin 方程[15]得到。

图2 Gemini Ⅶ 2390型比表面积测试仪Fig.2 Gemini Ⅶ 2390 specific surface area tester

1.4 分形维数的计算方法

林地土壤的孔隙结构由许多大小、形状各不相同的微孔、中孔和少量的大孔组成，其结构形状具有统计意义上的自相似性质[16]。描述林地土壤分形特征的定量参数是分形维数D，陶高梁等[17]的研究认为其分形维数在2～3，D越接近于2则表面越光滑；而D越接近于3，则表面越粗糙，不规整程度更高。

根据气体吸附等温线计算分形维数的方法，并利用低温氮气吸附试验所得数据，提出了基于FHH模型的分形维数理论计算方法，对在分形表面上的气体吸附有

lnV=Kln[ln(p0/p)]+c

(1)

式(1)中：V为相对吸附量,m3；p/p0为相对压力，p/p0>0.5；K为与吸附机理和分形维数D有关的常数；C为常数。

Avnir等[18]的研究表明，K的表达式为

K=D-3

(2)

根据测得的氮气等温吸附数据，按照式(2)进行数据处理，以ln[ln(p0/p)]为x轴，lnV为y轴作图并进行线性拟合，斜率为K，即可得FHH分形模型的分形维数D=K+3。

2 结果与分析

2.1 氮气等温吸附曲线

图3所示为不同平茬周期下沙柳林地不同深度土壤样品的吸附曲线。由图3可知，各曲线形态略有差别，但整体均呈反“S”形。在相对压力较低(0

0.95之后,吸附等温线发生跃阶,并且在接近饱和压力p/p0=1时氮气吸附量急速上升, 说明孔道形状为狭缝状，并且孔道分布不均匀。

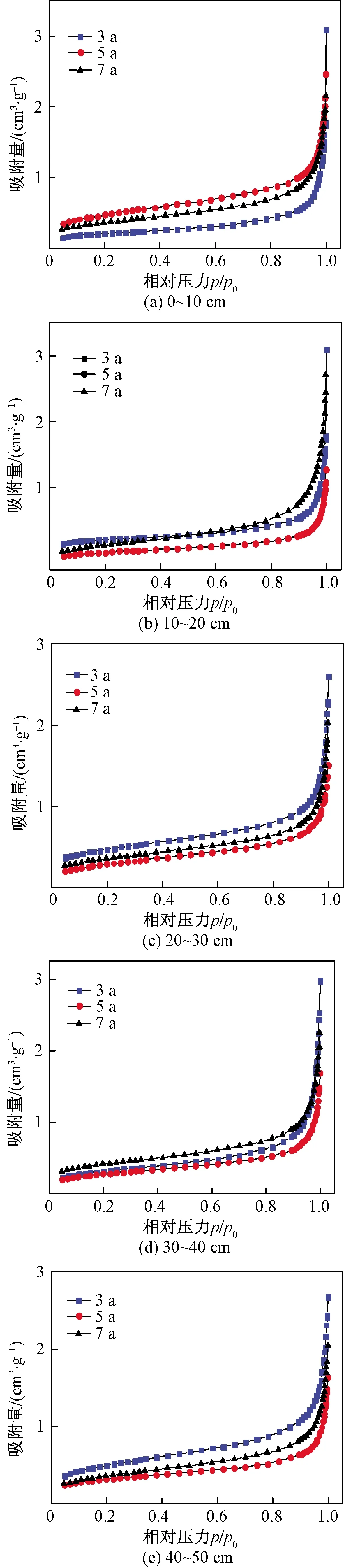
图3 不同平茬周期沙柳林地不同深度土壤的等温吸附曲线Fig.3 Isothermal adsorption curves of Salix psammophila forests at different depth in different stubble periods

2.2 孔隙结构参数分析

2.2.1 结构参数

表2所示为低温氮气吸附试验所得的孔隙结构数据，对比可知，相同平茬周期的沙柳林地土壤随着土层的加深各孔隙结构参数变化不一；随着沙柳平茬周期的延长，三个不同平茬周期下的林地土壤孔隙的BET比表面积和BJH总孔体积的平均值都有所增加，而平均孔径的均值无明显变化规律。SP-3 a(SP表示平茬周期)和SP-7 a的沙柳林地土壤孔隙结构参数变化范围较大，其中SP-7 a的比表面积和总孔体积最大，平均孔径最小，说明其孔隙内表面越不规则、孔隙结构越复杂；而SP-3 a的平均孔径最大，比表面积和总孔体积最小。根据国际纯粹与应用化学联合会(International Union of Pure and Applied Chemistry，IUPAC)孔隙分类准则可知，该研究区林地土壤孔径以中孔(直径为2～50 nm)为主。

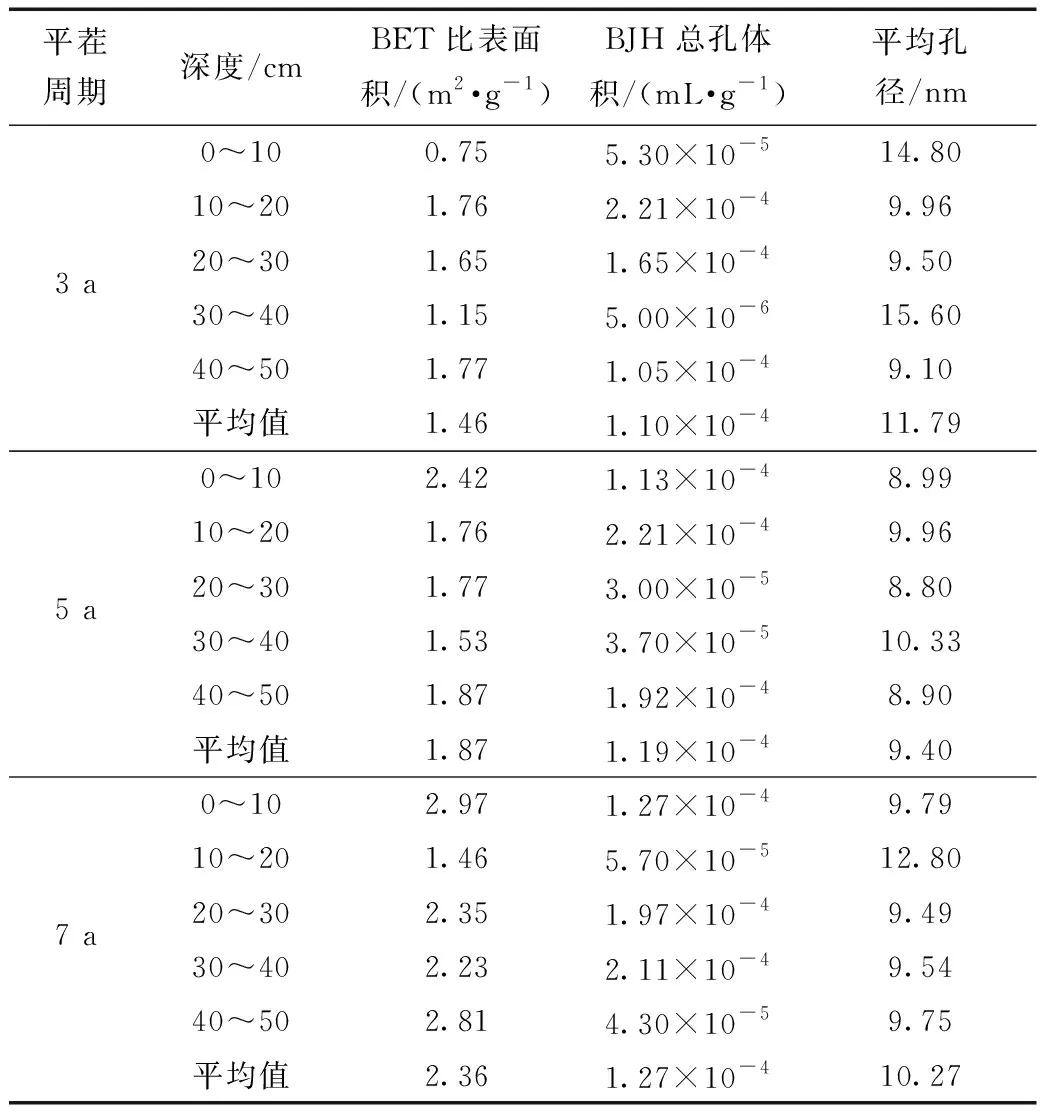
表2 低温氮气吸附试验所得孔隙结构参数Table 2 Paore structure prameters obtained by low temperature nitrogen adsorption test

2.2.2 孔隙结构参数之间的相关性分析

对得到的不同平茬周期下的沙柳林地土壤孔隙结构参数进行相关性分析，如图4所示，SP-3 a的沙柳林地土壤的BJH总孔体积、BET比表面积与平均孔径均呈负相关，而BJH总孔体积与BET比表面积呈正相关。说明对于SP-3 a的沙柳林地土壤而言，孔隙的平均孔径越小，BJH总孔体积和BJH比表面积越大，BJH总孔体积越大，BET比表面积也越大；对于SP-5 a的沙柳林地土壤，BET比表面积和平均孔径呈负相关，与总孔体积相关性较小；对于不同平茬周期的沙柳林地土壤，BET比表面积与平均孔径大体上都呈负相关，SP-3 a的R2最大为0.762 2；而SP-7 a的林地土壤，平均孔径和BJH总孔体积的相关性明显小于平均孔径和BET比表面积的相关性。综上可得出：SP-3 a的沙柳，对林地土壤的孔隙结构的影响最大，SP-5 a的沙柳，对林地土壤孔隙结构的影响最小，而SP-7 a的沙柳，只影响林地土壤的BET比表面积和平均孔径。

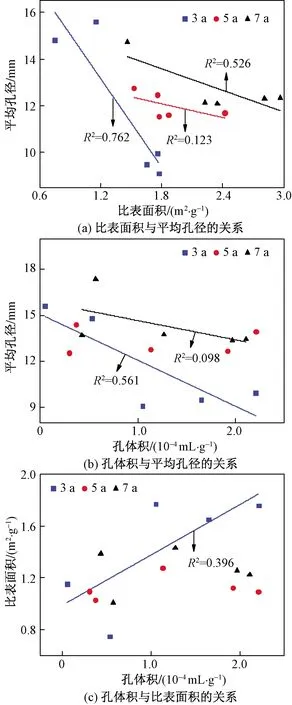
图4 孔隙结构参数间的关系Fig.4 Pore structure parameter diagram

2.3 FHH模型分析维数的计算结果

根据土壤样品的等温吸附曲线和孔径分布，将吸附相对压力分为三个区间，为0

表3 FHH模型计算的分形维数Table 3 Fractal dimension calculated by FHH model

2.4 分形维数与不同平茬周期沙柳林地土壤的孔隙结构参数的关系

2.4.1 分形维数与孔比表面积的关系

图5描述了不同平茬周期的沙柳林地土壤孔比表面积与分形维数D1、D2、D3的关系。由图5可知，对于SP-3 a和SP-5 a的林地土壤，所有分形维数与孔比表面积的相关性不明显，但都有增大趋势，并且D1的变化范围相对较大，SP-3 a和SP-7 a的土壤孔隙中有部分的孔的表面粗糙程度不一样；对于SP-7 a的林地土壤，分形维数D2与孔比表面积的相关系数R2=0.765 0，分形维数D1与孔比表面积的相关性不明显；分形维数D3与孔比表面积的相关系数R2=0.665 3。表明SP-7 a的沙柳林地土壤孔隙的分形维数与孔比表面积呈正相关，即分形维数D2、D3越大，孔比表面积就越大，孔的内部表面粗糙程度越大，孔隙结构分形也越明显，空间分布情况也越复杂。因此，分形维数可以很好地描述孔隙表面的不规则性和孔隙结构的复杂性特征。

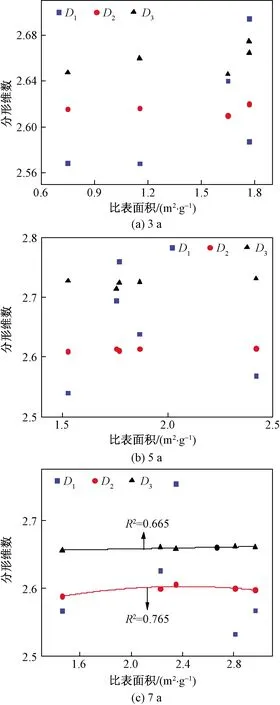
图5 不同平茬周期的沙柳林地土壤孔比表面积与分形维数的关系Fig.5 Relationship between soil pore specific surface area and fractal dimension of Salix psammophila forests with different flat periods

2.4.2 分形维数与总孔体积的关系

图6反映了不同平茬周期的沙柳林地土壤总孔体积与分形维数D1、D2、D3的关系。由图可知，分形维数D2、D3与SP-5 a的林地土壤的总孔体积呈正相关，相关系数分别为0.754 9和0.860 4，即分形维数越大，总孔体积越大；而与SP-3 a和SP-7 a的相关性不明显，但随分形维数D1、D2、D3的增大，总孔体积有增大趋势。表明不同平茬周期的林地土壤分形维数与总孔体积呈正相关，即分形维数越大，总孔体积越大。

图6 不同平茬周期的沙柳林地土壤总孔体积与分形维数的关系Fig.6 Relationship between total pore volume and fractal dimension of Salix psammophila forest in different flat periods

2.4.3 分形维数与平均孔径的关系

平均孔径是反映平均孔径大小的参数，平均孔径越小，表示孔隙结构中小孔数量越多，反之则大孔数量较多。图7描述了不同平茬周期的沙柳林地土壤孔隙的平均孔径与分形维数D1、D2、D3的关系。由图7可知，对于SP-7 a的沙柳林地土壤，分形维数D2、D3与平均孔径的相关性较好，相关系数分别为0.769 1和 0.752 6，而分形维数D1与平均孔径的相关性不明显；对于SP-5 a的沙柳林地土壤，分形维数D2与平均孔径的相关性较好，相关系数为0.830 7，D1、D3与平均孔径的相关性不明显；对于不同平茬周期的沙柳林地土壤的分形维数，随着分形维数的增大，平均孔径都有减小的趋势，说明可以通过分形维数来反映林地土壤孔隙结构中平均孔径的相对大小关系。正是由于林地土壤中小孔隙增多，使土壤的孔隙结构变得复杂，最终导致土壤分形维数增大。

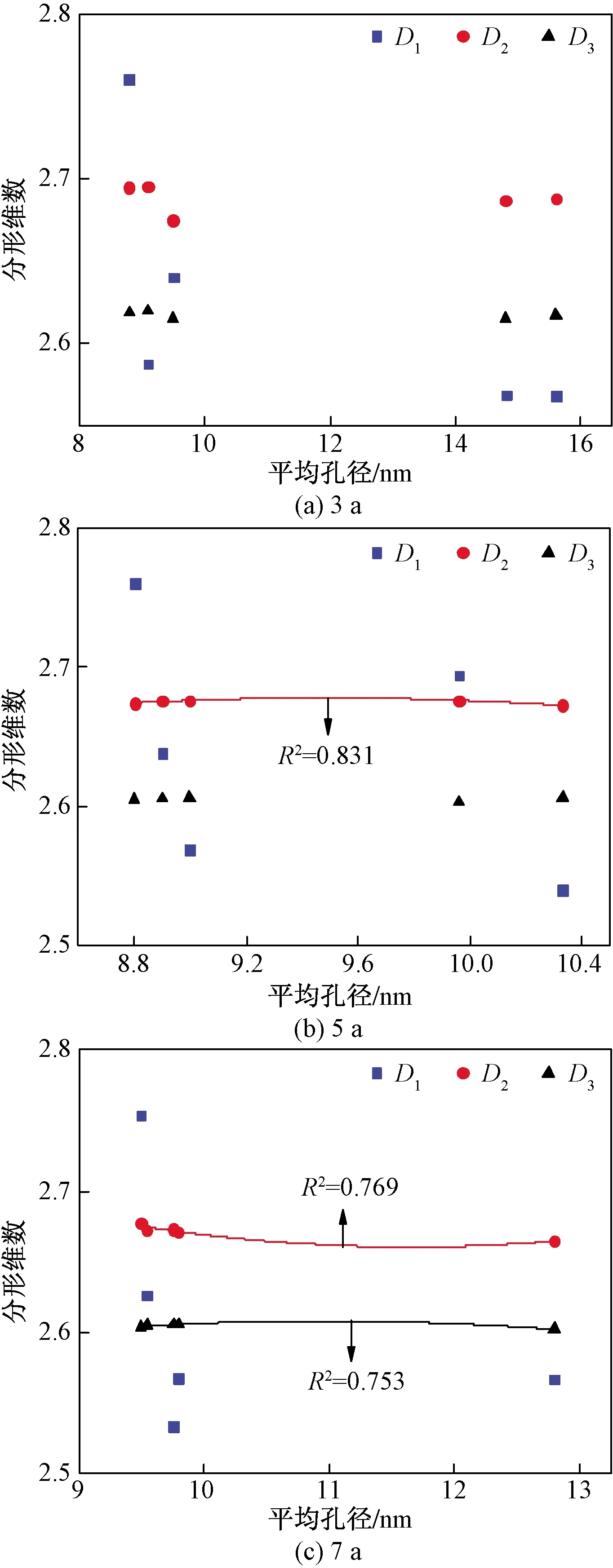
图7 不同平茬周期的沙柳林地土壤平均孔径与分形维数的关系Fig.7 Relationship between average pore size and fractal dimension of Salix psammophila forests with different flat periods

3 讨论

毛乌素沙地人工沙柳林定期的平茬复壮有效地改善了当地的生态环境，同时沙柳的平茬周期不仅会影响沙柳的可持续经营，还对土壤结构发育产生一定的影响。采用氮气吸附法及分形维数评价指标，来综合反映不同平茬周期沙柳林地土壤孔隙结构，也可对该研究区林地土壤孔隙表面复杂、粗糙和不规则程度进行描述。目前，氮气吸附法较多的运用于页岩孔隙结构[19-20]和煤体孔隙结构[21-22]；而将该方法用于林地土壤孔隙结构的研究相对较少，考虑到毛乌素沙地沙柳林地土壤中微孔和中孔较多的孔隙结构特征，将氮气吸附法用于毛乌素沙地沙柳林土壤孔隙结构和表征林地土壤表面的分形特征研究是可行的。

通过氮气吸附法测得林地土壤的吸附等温线的形状为反“S”形，与Paz-Ferreiro等[23]研究的黏性土壤的氮气吸附等温线相比，三者吸附量不同，但类型相似，均为IUPAC分类图中的Ⅱ型等温吸附曲线[24]，说明林地土壤具有很好的分形特征。通过氮气吸附实验测得的土壤孔隙结构参数间对比及相关性分析发现，孔隙结构参数的变化与平茬周期有密切关系，平茬周期为5 a时对林地土壤孔隙结构参数变化影响最小，土壤结构状况最好，保水保肥能力较好；平茬周期为7 a时对林地土壤孔隙结构参数变化影响最大，土壤结构状况较差，保水保肥能力也差。综上分析，从土壤结构变化来讲，平茬周期为5 a时较适宜，同海龙等[25]、段广东等[11]分别从平茬复壮以及防风效益角度研究得出毛乌素地人工沙柳林最优平茬时间为4a基本相符。可见合理的平茬周期不仅可实现沙柳灌丛复壮更新和持续发挥防风效益，还可使林地土壤结构得到改善。

实验结果表明，林地土壤孔隙结构的分形维数随土层深度变化不显著(α=0.05)。利用FHH模型法计算得到的林地土壤表面分形维数平均值为2.684 9，结果与党亚爱等[26]对黄土高原土壤剖面研究计算得到的体积分形维数相近，与胡康博等[7]利用热力学方法得到的河渠泥沙沉积物的分形维数范围也基本接近。通过分形维数与各孔隙结构参数的相关性分析得出，平茬周期为7 a时，林地土壤孔隙结构分形维数与各孔隙结构参数的相关性最强，对孔隙结构参数的变化更敏感；而平茬周期为5 a时，林地土壤孔隙结构分形维数与各孔隙结构参数之间的相关性最弱，进一步说明平茬周期为5 a时更有利于土壤结构的稳定形成。本研究以平茬周期来衡量其对林地土壤孔隙结构的影响，结果表明采用合理的平茬周期有利于林地土壤结构状况保持一定的稳定性，进一步使营造的沙柳人工林达到其自身的生产经营目的。

毛乌素沙地地形主要以丘间低地及沙丘为主，但本文主要以丘间低地处的土壤为研究对象，而在不同平茬周期下，沙柳对不同坡位处的土壤结构和表面分形特征有何影响，还需进一步的探究，也是团队接下来需要开展的工作。

4 结论

(1)该研究区的林地土壤孔径以中孔(2～50 nm)为主，有少量的微孔(≤2nm)和大孔(≥50 nm)。

(2)不同平茬周期的沙柳林地土壤孔隙结构分形特征明显，分形维数范围为2.497 1～2.779 7，平均为2.684 9，可较好地描述林地土壤孔隙表面和孔隙结构的分形特征，且不同平茬周期下林地土壤分形维数与各孔隙结构参数有密切关系，分形维数越大，孔隙表面越粗糙，不规整程度越高。

(3)对于该研究区沙柳人工林，平茬周期为5 a时较适宜林地土壤发育并保持结构稳定。