两指并联微操作手的动力学建模及仿真分析

耿冉冉,黄家才,王宇奇,温秀平

(1. 南京工程学院工业中心、创新创业学院, 江苏 南京 211167；2. 南京工程学院自动化学院, 江苏 南京 211167)

并联微操作手以其结构紧凑、运动惯性小、定位精度高、承载能力强等优势被广泛用于机械工程领域中的微加工、生物医学领域中的微创外科等方面[1-4].

国内外众多学者设计并研制了不同结构形式的并联微操作手,并进行了微操作手的动力学性能研究.文献[5]设计一种三自由度的具有桥式位移放大器的整体式柔性并联微操作手,通过数学建模和有限元分析建立微操作手的动力学模型；文献[6]采用模块化设计方法设计出一种Stewart柔性并联微操作手,以压电助动器为驱动元件,利用伪刚体模型建立并求解了微操作手的逆运动学方程,通过有限元仿真了解微操作手的六自由度运动能力；文献[7]研制了一种具有灵活抓取性能的四自由度微操作手,采用Cosserat Rod模型对微操作手进行了运动学建模,并利用仿真计算得出一组抓取实例；文献[8]设计了一种能够实现大工作空间的平面解耦并联微操作手,通过解析获得机构的运动学正反解,并建立机构的三维虚拟样机,仿真分析了其运动规律和特性.

两指微操作手相对于单指微操作手更具操作灵活性,可以实现对微小物体的夹取、调整位姿等微操作[9-11].直线超声电机具有运动精度高、输出力大、响应速度快、断电自锁等优点[12-13],近年来开始被应用于微操作领域.本文设计一种由直线超声电机驱动的两指并联微操作手,基于能量等效原理,采用分支结构建模法,分别计算4个子系统的动能和势能,利用拉格朗日方程建立两指并联微操作手的动力学模型.采用ADAMS动力学分析软件对两指并联微操作手进行反向动力学仿真和向前动力学仿真,得到两指并联微操作手在运行过程中的动态特性和重要参数.

1 两指并联微操作手的结构

本文所设计的由直线超声电机驱动的两指并联微操作手结构如图1所示,包括手臂、沿手臂中轴线均匀分布的3部直线超声电机、圆盘、柔性铰链、活动手指、固定手指、探针和底座等构件.其中,固定手指安装在手臂上始终静止不动,活动手指安装在圆盘上,通过直接输出直线运动的超声电机驱动实现2个转动自由度、1个移动自由度的运动.该两指并联微操作手的结构简单紧凑,便于装配,通过直线超声电机驱动能够达到较高的控制精度和较大的操作空间.

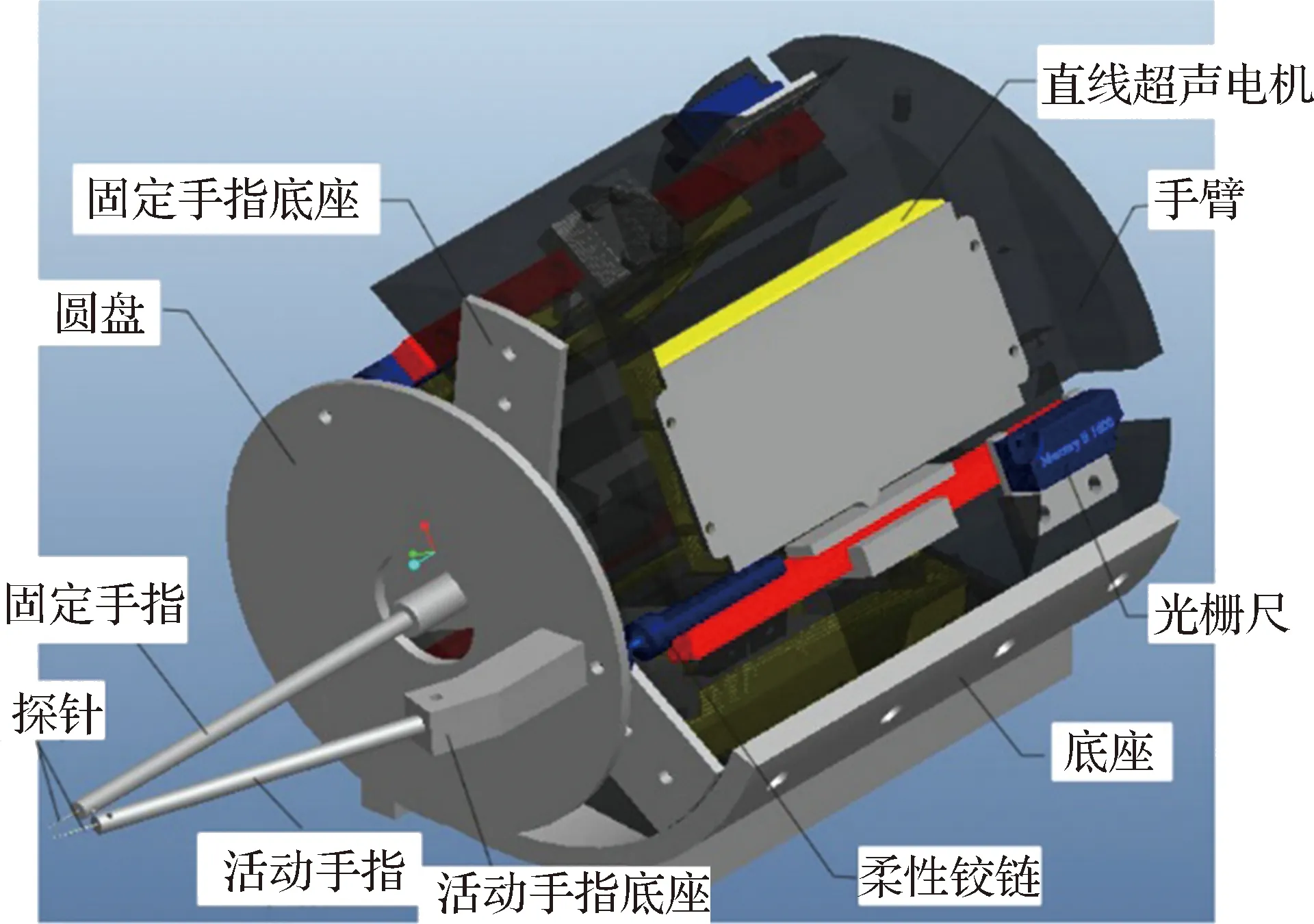
图1 两指并联微操作手结构示意图

2 两指并联微操作手动力学建模

依据两指并联微操作手的结构形式,构建物理模型如图2所示,全局坐标系{O}建立在两指并联微操作手主体圆柱形底面圆心处.3部电机的直线导轨和与其相对应联接的柔性铰链AiBi(i=1,2,3)构成3条相同且平行的运动链,电机输入由滑动副di表示,圆盘的中心为C,半径为R.活动手指B1E与圆盘夹角为60°,点E为两指并联微操作手的操作末端.

图2 两指并联微操作手的物理模型

基于能量等效原理,采用分支结构建模法建立两指并联微操作手的动力学模型,其中,3个柔性铰链为会发生弹性变形的弹性体,其余部件(如电机导轨、圆盘、手指等)为刚性体.

2.1 拉格朗日方程动力学建模

两指并联微操作手系统属于完整约束系统,采用拉格朗日方法对其进行动力学建模,可得到相对简洁的动力学模型.为便于描述系统能量分布,将操作手切分为4个子系统,如图3所示,分别为1个由圆盘及活动手指组成的圆盘手指子系统和3个由直线超声电机驱动的滑移副及柔性铰链组成的运动链子系统.

图3 4个子系统分割示意图

将两指并联微操作手的末端输出坐标xE=[xEyEzE]T作为拉格朗日方程里的广义坐标.该系统中的主动力只有非有势力,引入拉格朗日函数L=T-V,则其动力学普遍方程为：

(1)

式中：T、V分别为系统的动能和势能；F1、F2、F3分别为3条运动链所受的力.

2.2 运动链子系统的动能和势能

在直线超声电机驱动下,柔性铰链发生弯曲变形,由于转动角度很小,转动动能远小于平动动能,因此只考虑柔性铰链的平动动能.每条运动链的动能为导轨的动能与柔性铰链的动能之和,第i条运动支链的动能为：

(2)

式中：md、mr分别为导轨的质量和柔性铰链的质量;di为可由文献[14]中提出的微操作手运动学模型里转换成输出坐标的表达式.

两指并联微操作手能够产生运动的关键在于柔性铰链受到力矩作用后会发生弯曲变形,进而带动圆盘转动,使操作末端产生运动.该系统的势能只有柔性铰链的弹性势能,第i条运动链的势能为：

(3)

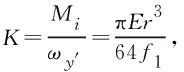
2.3 圆盘手指子系统

圆盘手指子系统各部分皆为刚体,只需考虑动能,其总动能为：

Tm=Tp+Th

(4)

式中，Tp、Th分别为圆盘手指子系统的平动动能与转动动能.

平动动能为：

(5)

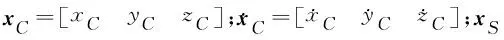
圆盘与手指质心的速度向量与系统输出位移向量xE的关系分别为：

(6)

(7)

圆盘手指子系统的转动动能为：

(8)

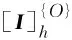
由于圆盘在z轴方向上没有转动,因此ωz=0,则有：

(9)

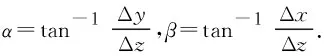
(10)

在活动手指质心S处建立局部坐标{S},如图4所示.

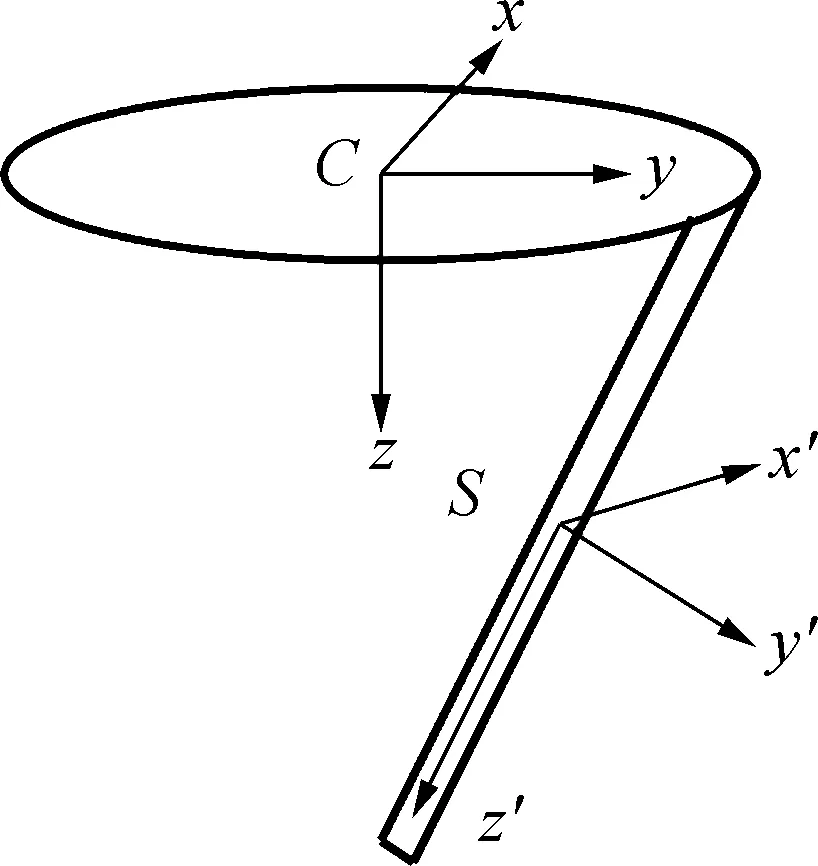
图4 活动平台子系统

根据平行轴定理,活动手指在坐标系{C}中的转动惯量为：

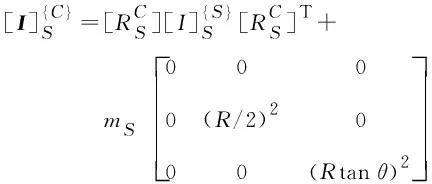
(11)

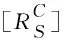
(12)

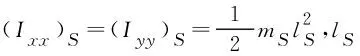
(13)

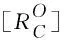
通过计算出的各个子系统动能和势能,将动能和势能之和带入拉格朗日方程式(1),即可获得该两指并联微操作手的动力学模型.

3 两指并联微操作手动力学仿真

在得到两指并联微操作手刚柔耦合动力学模型后,采用ADAMS动力学分析软件对两指并联微操作手的动态响应参数作进一步的仿真计算.在仿真分析过程中需要先将图1所示的两指并联微操作手三维模型中的柔性铰链进行柔性化处理,才能建立两指并联微操作手的刚柔耦合仿真模型.

3.1 反向动力学仿真分析

反向动力学仿真分析即通过设置位移驱动函数,使两指并联微操作手的操作末端由初始位置到达预定位置,仿真计算得到两指并联微操作手输入构件的运行状态.令活动手指末端点用0.1 s的时间从坐标原点平缓运动到(1.0,1.0,1.0)的位置,通过动力学仿真计算得到3个直线超声电机导轨的质心位移、速度变化曲线，如图5所示,图5中导

(a) 导轨1

(b) 导轨2

(c) 导轨3

轨的序号与图2中运动链的序号一致.由于导轨只能沿z轴方向运动,因此得出的位移、速度曲线都是沿z轴方向的.由图5可得,为实现操作末端的定位运动,需驱动运动链1、2、3上的电机沿z轴方向以15 mm/s左右的速度分别移动0.44、0.82、1.82 mm.

3.2 向前动力学仿真分析

向前动力学仿真分析即通过对导轨设置位移驱动函数,仿真计算得到两指并联微操作手操作末端的运行状态.假设运动链2上的导轨用0.1 s的时间沿z轴方向以15 mm/s的最大速度平缓移动1 mm,同时运动链1、3不产生运动.图6为动力学仿真计算得到的操作末端在x、y、z轴的位移变化曲线.由图6可得,操作末端点沿x、y、z轴分别移动了0.57、0.99和0.33 mm.

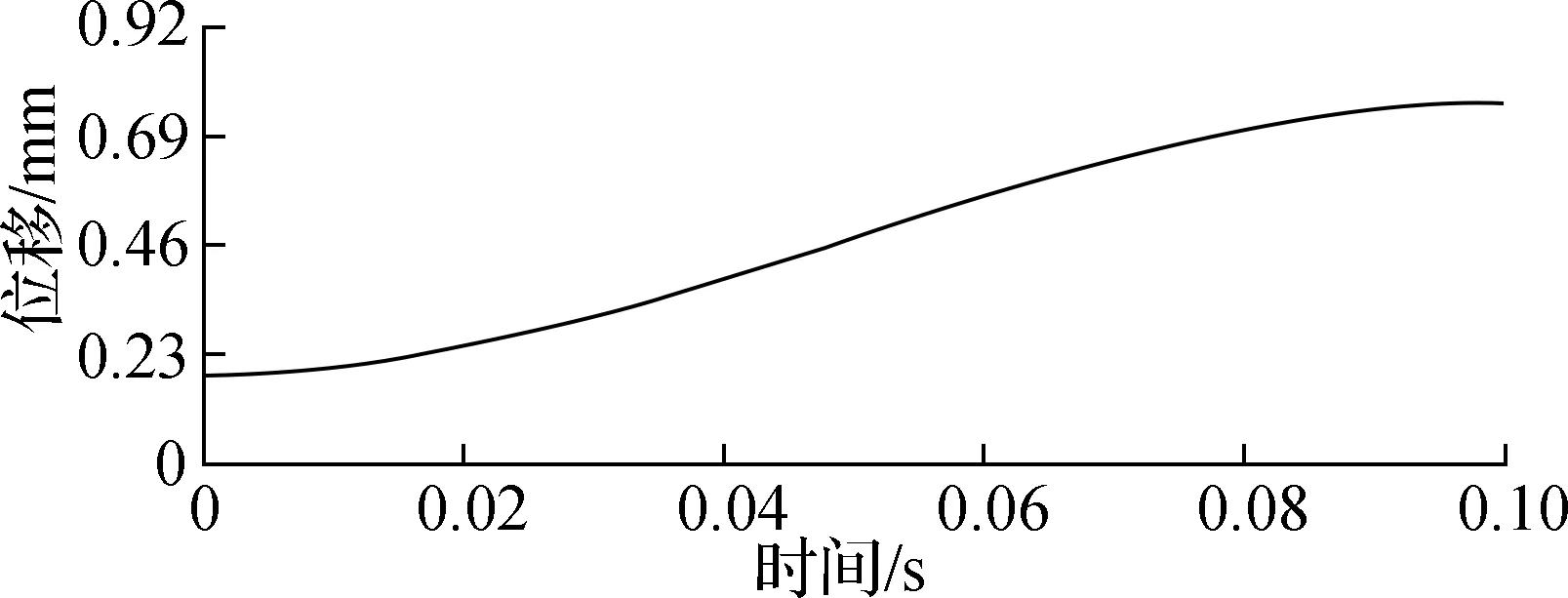
(a) x轴

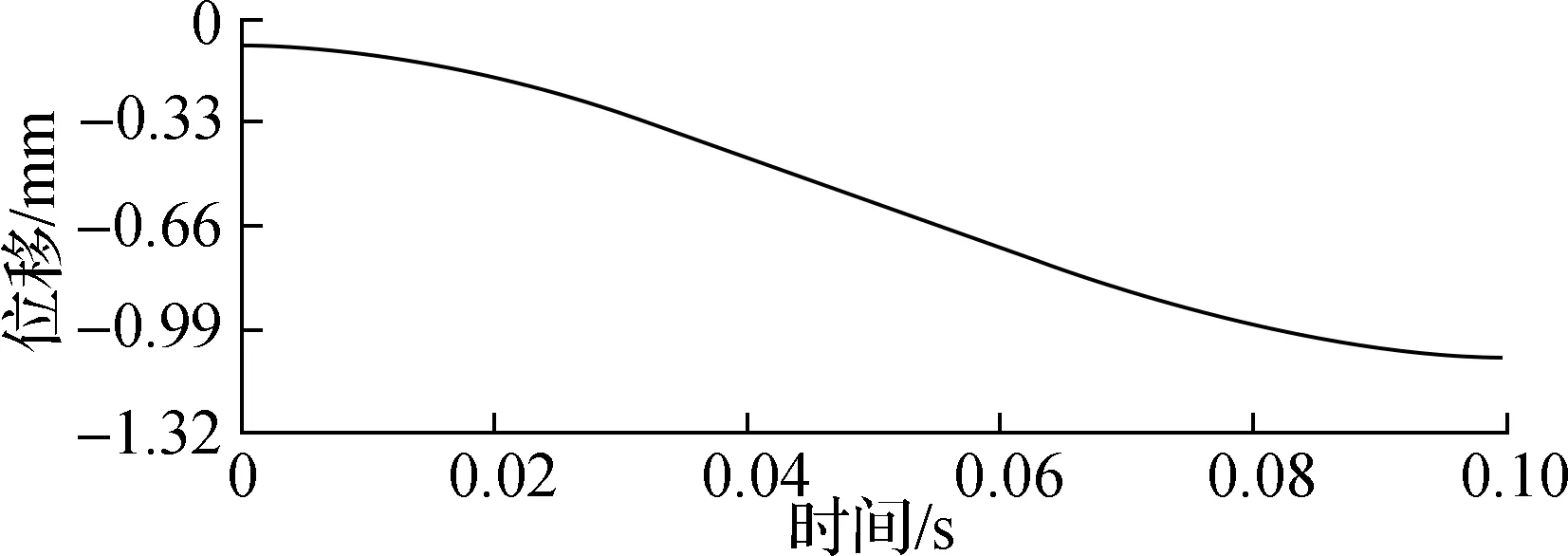
(b) y轴

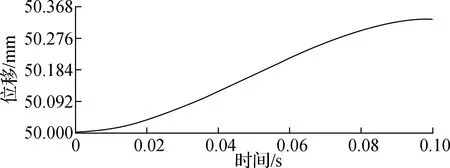
(c) z轴

图7为动力学仿真计算得到的操作末端在x、y、z轴的速度变化曲线.由图7可得,操作末端点沿x、y、z轴的最大移动速度分别为18.75、22.75、5.43 mm/s.

(a) x轴

(b) y轴

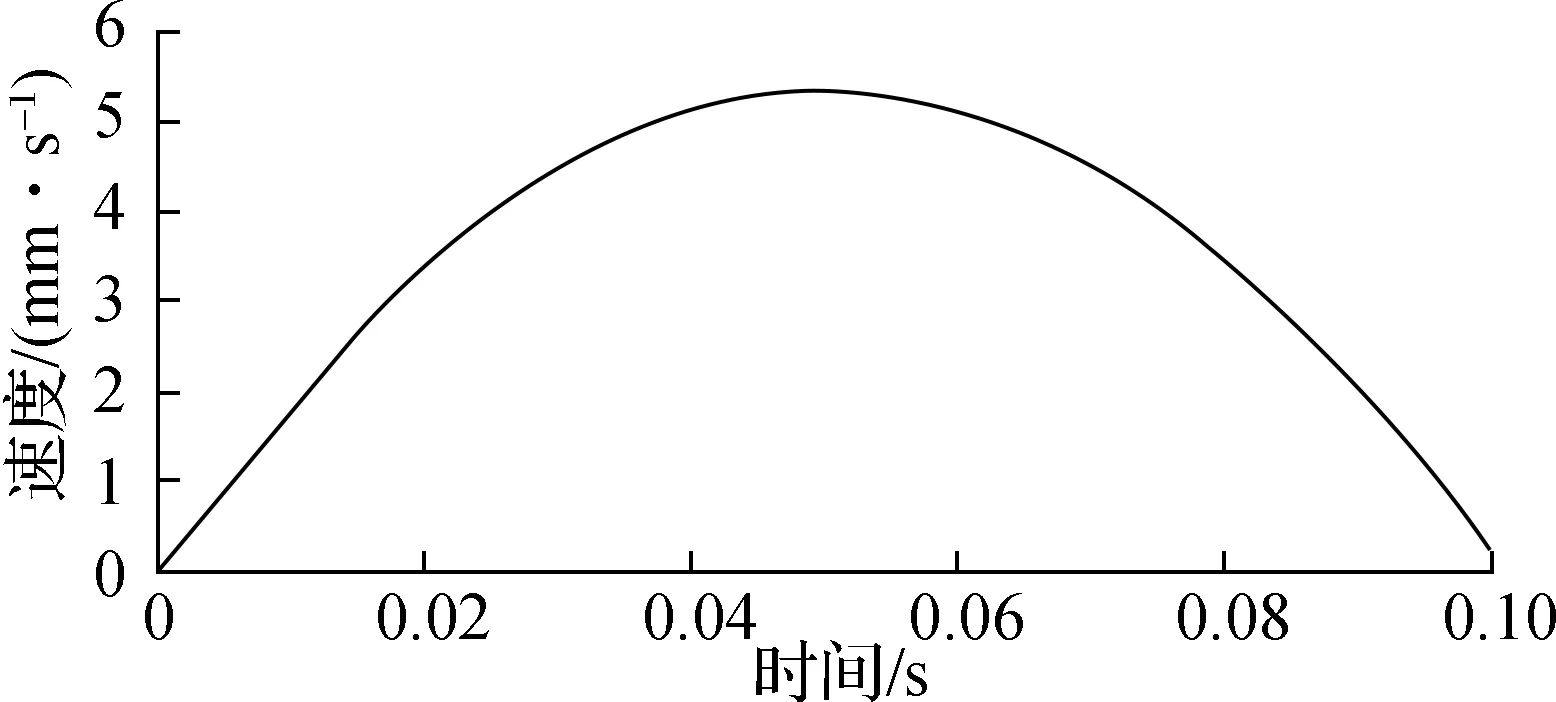
(c) z轴

4 结语

本文提出一种由直线超声电机驱动的两指并联微操作手,根据能量等效原理,利用分支结构建模法将两指并联微操作手系统分割为3个运动链子系统和1个圆盘手指子系统,分别获得其动能和势能.两指并联微操作手的构件都是直接或间接固定在底座上的,可以忽略系统的重力势能,只需考虑柔性铰链的弹性势能作为系统的势能.将系统的动能与势能带入拉格朗日方程即可得到两指并联微操作手的动力学模型.通过对两指并联微操作手设置位移驱动函数,利用ADAMS软件分别对两指并联微操作手进行反向动力学和向前动力学仿真分析,得到电机输入与末端输出之间的动态特性和相关参数,包括位移响应、速度响应等,该计算结果有助于指导两指并联微操作手的可行性分析.