也谈数学作业的有效性

江苏省太仓市明德高级中学 (215400) 顾丽琴

前不久，笔者在网上无意间看到这样一句对数理化评价的话：物理难，化学繁，数学作业做不完.作为一名高中数学教师，自然对“数学做不完”颇有想法——数学作业为什么做不完？没完没了的作业真的有效吗？作为数学教师该如何提高作业的有效性？

一、高中数学作业的现状分析

数学一向被认为高考最重要的科目之一，无论是家长还是学校领导，都认为数学处于“一荣俱荣，一损俱损”的地位， “得数学者得高考”成了人们的信条，于是学生的数学课业负担逐年加重，“数学作业做不完”便是当今数学教学的真实写照.

那么，高中阶段教师为什么要布置这么多的数学作业呢？笔者以为主要有三个原因：

一是学校或教师的攀比心理作怪所致.虽然上级教育部门禁止教育单位给学生成绩排名，给学校的平均分排名，但学校为了所谓的教学成绩，排名依然盛行，班级与班级之间进行竞争，学校与学校之间进行竞争已成为当今教育的常态.地方教育局把升学压力转加给校长，校长把升学压力转加给教师，教师再把升学压力转加给学生，而教师让学生提高分数的唯一法宝就是多练，用行话叫“精讲多练”.于是处于“食物链底端”的学生无奈的被沦落为“作业的奴隶”.

二是教师以为“熟能生巧”所致.熟能生巧，在一定范围内具有一定的积极意义，但它并非教学规律，世间任何事物物极必反.在日常教学中不难发现，教师往往讲了一个数学知识点或一类问题后，就让学生围绕这个知识点或这类问题反复操练，把“举一反三”变成了“举一反十”，肆意夸大练习的效果，置学生的个人感受于不顾.这种作业模式不仅磨灭了学生的学习热情，而且容易使学生形成思维定势，最终很可能产生“熟能生笨”的负面效果.

三是学校的“月考制”所致.在应试教育愈演愈烈的今天，学校似乎不仅仅是学生学习的场所，更是学生没有硝烟的战场.每周一小考，每月一大考如紧箍咒般折磨着教师和学生，教师与学生为了所谓的排名，哪敢懈怠.于是什么数学滚动练，数学小题练，数学保温练，数学中档练，数学提高练等五花八门的“练习品种”应运而生，使学生每天永远处于“写不完作业”的状态中.

既然这种“写不完的作业”模式已经大大降低了学生的学习效率，并伤害了学生的学习数学的积极性，那么作为教师的我们该如何给布置有效的作业的？

二、提高数学作业有效性的几点措施

众所周知，数学作业是数学课堂教学的延续，从学生的认知规律看，可以起到巩固已学知识，发展学生能力的作用，因此数学作业是数学教学的重要组成部分，也是教师备课的重要部分，教师不仅要备好课堂所教内容，也要备好课后作业，要让学生乐于作业，并让作业产生教学效益.我们既要严格控制作业的数量，更要把好作业的质量关，真正让学生练有所获.基于此，笔者谈谈提高数学作业有效性的几个措施.

1.作业的内容要有针对性

作业内容的针对性，主要包含两个方面：一是作业应该针对当堂所学内容，尤其是基础年级，一般应遵循“课上教师讲什么，课后学生练什么”的原则，教师可以针对知识点编排作业，也可以针对基本题型编排作业，切忌“超纲”，不宜搞“滚动练”；二是所布置的作业要针对数学学习的核心素养，应明确每一道作业题是为哪种数学核心素养的编制的.

例如，教师在完成人教A版普通高中数学必修第二册的第38页至第39页的《6.4.1平面几何中的向量方法》的课堂教学后，应围绕着本节课的教学核心，即如何运用平面向量来处理平面几何问题来编制学生作业，或许涉及这一内容的题型在以后的各级各类的考试中很少出现，但秉着提升学生数学核心素养的原则，教师还是要精选针对性较强的题目让学生练习.通过练习来培养学生的转化能力和逻辑推理的核心素养.下面给出两种题型供大家参考.

A.正方形 B.矩形

C.菱形 D.等腰梯形

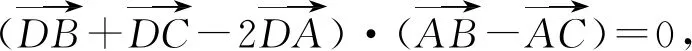
作业题2 已知正方形ABCD,E、F分别是CD、AD的中点,BE、CF交于点P,连接AP.用向量法证明:(1)BE⊥CF; (2)AP=AB.

作业题1是针对于平面向量的基本运算及其几何意义而设置的，主要训练学生的向量的基本运算技能和对向量运算的几何意义的理解；作业2是针对向量的坐标运算设置的，要求学生能用建立坐标系的方法并借助向量的坐标运算解决平面几何的证明问题，这两个作业题都紧紧围绕平面几何中的向量方法这个主题，难度虽然不大，但能起到巩固已学知识的作用，通过练习可以提升学生的逻辑推理和数学运算素养，可见，作业量不在于多，而在于精，在于具有针对性与目的性，这样的作业对学生才有效.

2.作业的难度要有层次性

因材施教是基本的教学原则.某个数学问题，对于有些学生来说，或许教师一点就通，而对于有些学生来说，教师纵然讲解三遍，他们却仍处于似懂非懂的状态，这时教师就要放宽教学要求，因材施教，不可搞一刀切，搞标准化，否则严重影响到学生的最优发展.因此，针对不同的学生群体，教师布置作业应有的放矢，要分层.如何分层，教师可依据所学的内容和教学目的以及题型变化来实施.可以将作业设置成A,B,C三种层次，A层次较为基础，B层次为中等要求，C层次为较高要求，让学生根据自己的实际水平加以选择相应的作业完成.也可以针对考试难度，再题型上设计不同要求，供学生们练习.

例如，在上完了人教A版普通高中数学必修第二册的第42页至第54页的《6.4.3正弦定理、余弦定理》的内容后，教师可以从知识的简单应用，知识的综合应用和知识的创新应用上设置作业题，让学生根据自己的实际水平与需要选择性的加以完成.

图1

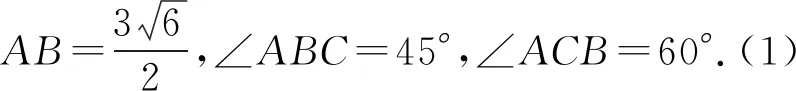
作业题3(B层次) 在△ABC中，角A,B,C的对边分别为a,b,c，且(sinA+sinC)(a-c)=sinB(b-c).(1)求A； (2)如果△ABC是锐角三角形，求sin2B+sin2C的取值范围.

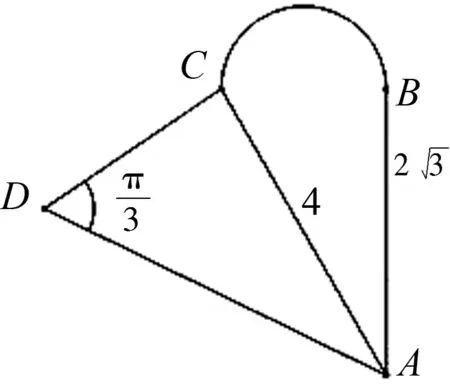
图2

上面四个作业题中，只要求学生根据自己的实际情况选择两个题目完成，这样就有六种搭配供选择，即便是对于基础薄弱的学生选择前两个A层次的题目作为作业题，也能达到巩固正弦定理与余弦定理的综合应用的目的.而作业题4是针对学有余力的学生设置的，借助这道题可以提升这部分学生的综合素养与创新能力，并激发他们对数学的热爱之情与成就感.

3.作业的形式要有多样性

长期以来，数学作业给人的印象就是让学生做数学题，书本上的几道题目，教辅书上的练习题，以及教师翻印的练习卷，是学生作业的主要形式，人们似乎认为，只有多做数学题才能学好数学，把学数学与做题目等价起来，于是学生成了一台“解题机器”，一台“被动做题”的“解题机器”，久而久之，他们会对解题产生厌恶感，更不利于把他们培养成复合型创新型人才.基于此，笔者在想：能否将作业形式从“单一性”向“多样性”转化呢？

当某一个单元的内容学完后，我们不妨给学生更多的作业形式和思维空间，作业可以是一篇学习心得，可以是一篇小论文，可以是强调探究过程的研究性合作性学习，也可以是对课本例题或相关高考题的研究，等等，如《谈谈对本单元的学习感受或收获》、《对一道课本例题进一步探究》，《一道课本习题的一题多解(一题多变)》，《我来编几个练习题》、《寻找生活中的函数模型》等，这种不拘一格的作业形式既能激发学生的学习兴趣，又能培养他们的创新精神，从而达到提升学生数学核心素养的最终目的，我们何乐而不为呢？

例如，当学生完成了《数列》单元的学习后，教师可以提供如下作业题供学生选择：

作业题1 请谈谈等差数列与等比数列的区别与联系(小论文形式).

作业题2 请编拟一份半小时的数列小练习，并附上答案(试题形式).

作业题3 生活中的数列问题(研究性学习形式，可以合作完成).

作业题4 数列求和方法知多少 (专题总结的形式).

作业题5 数列不等式问题专题研究 (小论文形式).

值得一提的是，这些形式多样的作业题的编制，教师必须深思熟虑，必须紧扣教学目标，必须符合学生的实际认知水平，对学生而言要具有可行性，能让不同层次的学生选到适合自己的题目.这些题目是对学生所求知识的检验，更是对他们能力的挑战.

三、结束语

作为战斗在第一线的数学教师，我们应该转变观念，积极相应“减负”号召，从减少学生的作业数量做起，从提高学生的作业质量做起，让数学作业真正发挥其应有的作用，从而实现“师生共赢”.