基于惯性权值非线性递减的改进粒子群算法*

华 勇，王双园，白国振，李炳初

(上海理工大学 机械工程学院，上海 200093)

0 引 言

粒子群优化算法(Particle Swarm Optimization，PSO)是由Eberhart和Kennedy于1995年提出的一种新的全局优化算法[1]，它源自于对鸟类捕食行为的模拟。目前，PSO算法已经发展为一种通用的优化进化算法，并被广泛应用于神经网络训练、模糊系统控制、人工智能等领域[2-3]。但粒子群优化算法始终存在着早熟收敛、收敛速度慢甚至不收敛等一系列问题，针对这些存在的问题，国内外众多学者提出了许多改进策略，主要有以下3种策略：

(1)对粒子的速度和位置采用不同的参数策略来更新，如采用线性惯性权值动态变化策略[4-5]，使算法可以在迭代初期以较快的速度寻找到粒子最优解的大致位置，随着迭代的进行而惯性权重逐渐减小，粒子速度开始减慢，粒子开始进行局部高精度搜索。该策略的主要特点是速度和位置的更新由粒子自身经验和群体经验指导。

(2)引入变异策略。粒子群算法结合生物种群进化里的变异操作能够提高算法的开拓寻优能力，并能够有效地克服收敛早熟。如采用柯西变异的策略[6]，以一定的概率选中粒子进行柯西变异，而未被选中的粒子则采用不同子群进化策略，可以有效地提高算法的收敛性能与效率。但变异策略也存在着诸多问题，何时变异及变异概率的确定等问题在实际求解问题中都难以确定。

(3)混合智能算法。粒子群算法结合其他算法，以达到优势互补的效果，可有效地提高算法的性能。如在粒子群算法中引入了鸡群算法[7]，使得改进后的混合粒子群算法优化在机器人路径规划中得到很好的应用。

在参考粒子群算法的各种改进策略基础上，提出了一种基于自然选择和惯性权值非线性递减的粒子群算法。在算法的迭代过程中，粒子最大速度和惯性权值非线性递减以保证粒子的全局寻优能力与局部能力相互平衡，权重控制因子的调整可以保证最大惯性权值与最小惯性权值在种群进化过程中所占的比例；为了提高算法进化过程中种群的多样性，引入二阶振荡策略，考虑粒子群算法的适用性问题，进一步地将遗传算法中的自然选择机制加入其中，有效地提高算法的寻优精度。基准测试函数的仿真实验结果表明，所提出的算法有效地克服了粒子群算法过早收敛和不收敛的问题，使粒子的寻优能力和搜索精度得到显著提升，相比于文献[8]中所提出的改进粒子群算法，本文所提出的算法优化性能更佳。

1 粒子群算法的基本原理

1.1 基本粒子群算法

粒子群优化算法具有独特的搜索机制，是受鸟群捕食行为的启发而提出来的一种群体智能优化算法。其关键在于每个粒子在解空间内根据自己的记忆和从其他粒子获取的社会信息来更新自己的位置，通过个体之间的竞争与合作，实现在复杂空间中最优解的寻找。该算法中每个问题的潜在解都是搜索空间中的一只鸟，也简称为粒子。该算法的数学理论描述为:设在一个D维搜索空间中，每个粒子是一个点，粒子规模为N，第i个粒子的位置矢量可以描述为xi=(xi1,xi2,…,xiD)，速度矢量可描述为vi=(vi1,vi2,…,viD)，第i个粒子搜索到的最优位置为pi=(pi1,pi2,…,piD)，称为个体极值，表示粒子的个体经验；整个种群搜索到的最优位置为pg=(pg1,pg2,…,pgD)，称为全局极值，表示粒子的群体经验。粒子的速度和位置更新公式如下:

(1)

其中，i=1,2,…,N，N为粒子规模；d=1,2,…,D，D为解空间的维数，即自变量的个数；w为惯性权重；c1为种群粒子的个体学习因子，c2为种群粒子的社会学习因子，分别用于调节粒子向个体极值与全局极值方向的最大步长，体现了粒子间的信息共享与合作；r1与r2为在[0,1]区间上均匀分布的两个随机数。

1.2 权重因子线性变化的粒子群算法LDWPSO

为了平衡全局搜索与局部搜索，在不同的搜索阶段采用不同的惯性权重，即权重w随着迭代次数的增加而线性减小，以使算法在搜索初期时拥有较大的惯性权重，有利于搜索整个解空间，不易陷入局部最优值。而在搜索后期，种群拥有较小的惯性权重，有利于种群对局部进行精细化挖掘，使粒子可以较快地收敛于全局最优值，其数学描述如式(2)所示[5]：

(2)

1.3 带压缩因子的粒子群算法CPSO

将标准粒子群算法中速度更新公式的每一项都与学习因子牵连起来，在一定程度上，粒子的自我学习价值与社会学习价值也能作用在速度惯性的变化上，其数学描述如式(3)所示[9-10]：

(3)

压缩因子按照下式计算:

(4)

其中，φ=c1+c2，通常当c1=c2=2.05，λ=0.729时，算法具有较好的性能。

2 改进的粒子群算法MPSO

2.1 惯性权值非线性变化策略

惯性权重是PSO算法中极其重要的参数，它描述了粒子上一代速度对当前代速度的影响，控制其取值大小可有效地调节平衡PSO算法的全局与局部寻优能力。当惯性权值较大时，全局寻优能力较强，局部寻优能力较弱；当惯性权重较小时，局部寻优能力较强，而全局寻优能力将减弱。考虑切比雪夫滤波器幅频响应曲线模型在线性和非线性行为之间表现出极好的过渡性，提出了一种基于切比雪夫滤波器惯性权重非线性变化策略，并引入权重控制因子，通过调节该控制因子的大小进而来调整最大惯性权值在种群进化过程中所占的比例，能够保证粒子群在初始状态时以较大的惯性权值进行全局开发性搜索，而在迭代后期又以较小的固定权值进行更为精细化的局部寻优，其数学模型如式(5)所示:

(5)

其中，K为权重控制因子，t为种群当前进化代数，T为种群总的进化代数。在算法迭代初始，粒子的权值可以取得最大值0.95，有利于前期的全局搜索，而随着迭代次数的增加，粒子的权值逐渐趋近最小值0.4，此时可以更好地进行局部精细化搜索。

2.2 粒子最大速度非线性递减策略

粒子最大速度的设置非常重要，较大的速度有利于种群进行全局的开发，但粒子速度过大，会导致粒子在搜索的过程中错过全局最优解；与之相反，较小的速度有助于种群进行局部搜索，但速度过小，会导致粒子不能够在解空间内进行充分探索，从而陷入局部最优的可能性提高。为了进一步提高PSO算法的性能，防止因为粒子飞离搜索空间而造成种群多样性减小，进而提出了一种粒子最大速度非线性递减策略。粒子的最大速度在随着种群迭代的进行过程中呈现非线性减小，可使粒子有效地避免因为过大的速度而落入边界区域进行无效地搜索。粒子最大速度非线性递减策略数学模型如式(6)所示：

(6)

其中，vmax与vmin分别为种群粒子最大速度的最大值与最小值，它们的取值由标准测试函数定义域确定。

2.3 自然选择原理

考虑到PSO算法优化性能会受到的随机因素影响较多，为了提高算法的适用性，结合遗传算法中的选择思想，在上述几种改进策略的基础上加入自然选择机制，其基本思想为每次迭代过程中将整个粒子群按照适应值的大小来进行排序，并用群体中适应值最好的一半的粒子的速度与位置来替换群体中适应值最差的一半的粒子的位置和速度，在这一过程中保留原来个体记忆的最优值，来提高粒子接近最优值的几率。

2.4 粒子二阶振荡策略

粒子群算法在迭代过程中是呈现渐进收敛的，整个迭代过程中种群的多样性势必会有减小的趋势，这不利于粒子寻求最优解的几率提高，在标准粒子群算法的基础上，采用文献[11]中所述的方法，对粒子速度更新进行二阶振荡处理，以进一步提高种群的多样性，改善算法的全局与局部收敛平衡性能。其速度更新方程如下：

(7)

3 改进粒子群算法的流程

改进粒子群算法的主要实现步骤如下:

(1)设定各参数，初始化种群中各粒子的位置和速度；

(2)计算种群中每个粒子的适应度值，初始化种群个体最优值和全局最优值，将当前各粒子的位置和适应度值存储在各个粒子的pi，将当前所有pbest中适应度值最优个体的位置和适应度值存储于pg中；

(3)根据式(5)对惯性权值进行更新；

(4)根据式(7)以及式(1)中的位置更新公式进行粒子的速度和位置更新；

(5)根据式(6)对粒子的最大速度进行更新，以保证算法的收敛性能；

(6)比较粒子适应度值与其经历过的最好的位置进行比较，更新粒子当前的个体最优值；

(7)比较粒子适应度值与种群全局极值，更新粒子当前的全局最优值；

(8)将种群适应度值的大小进行排序，用群体中最好的一半的粒子的速度和位置替换最差的一半的粒子的速度和位置，同时把持种群中个体最优值与全局最优值记忆不变；

(9)若满足迭代停止条件，则搜索结束；若不满足迭代停止条件，则返回步骤(3)。

4 仿真实验及结果分析

4.1 权重控制因子K的确定

首先设计了一个实验，讨论了所提算法惯性权值调整策略中权重控制因子K的取值。文献[13]指出当较大的惯性权值在种群进化过程中所占比例超过二分之一迭代数时，将不利于保证解的精度，因为迭代后期主要是以粒子进行精细化搜索为主。针对此，改进算法采用30维Sphere函数对K从3～8的几个不同取值的收敛结果进行比较，参数设计见表3所示。对应于K值的不同取值，文中改进算法都独立运行20次，并计算其平均性能，实验结果如表1所示。

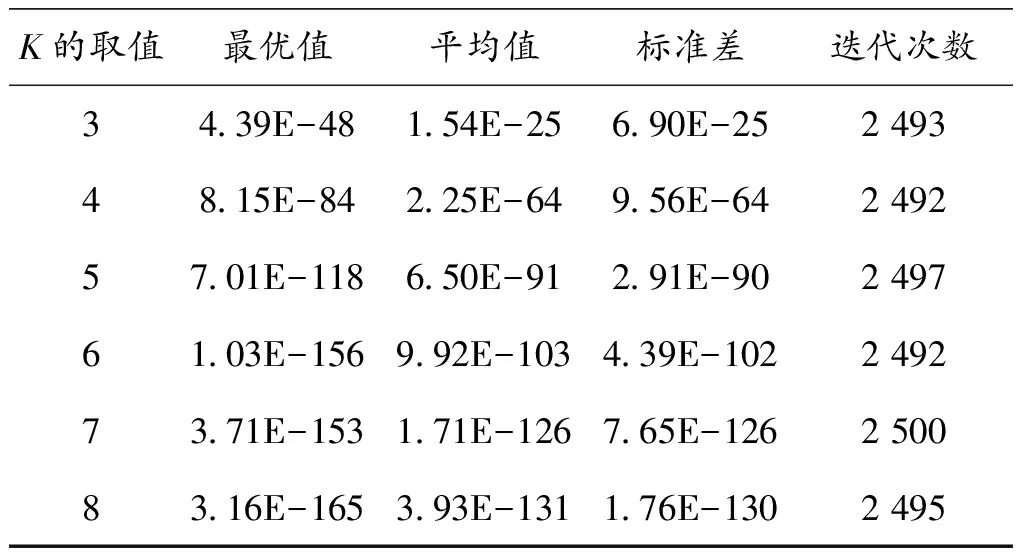
表1 30维时不同K值对Sphere函数的实验结果

从表1可以看出：当K=8的时候，算法的收敛性能最优，其所达到的收敛精度与稳定性也是最高的。这也证明了粒子群算法在迭代后期需要以较小的惯性权值进行局部精细化搜索的重要性。从表1中也可以看出，随着K值的不断增大，即较小的惯性权重值在种群进化过程中所占比重越大，文中改进算法搜索到的最优解精度也随之提高，但迭代次数都未有较大的波动，因此，在后面的仿真实验设计中，文中改进算法的K值均取为8。

4.2 仿真试验设计

为了对所提算法的性能进行分析和验证，选取8个典型Benchmark测试函数来进行分析，将其测试结果与标准粒子群算法(PSO)、惯性权值线性变化的粒子群算法(LDWPSO)和带压缩因子的粒子群算法(CPSO)的测试结果进行比较,每个函数的参数设置如表2所示，每个算法的参数设置如表3所示。考虑到算法每次运行的随机性，对于每个测试函数所采用的不同优化算法都重复独立运行 30次，取所得最优解的均值与方差作为最终的优化结果。

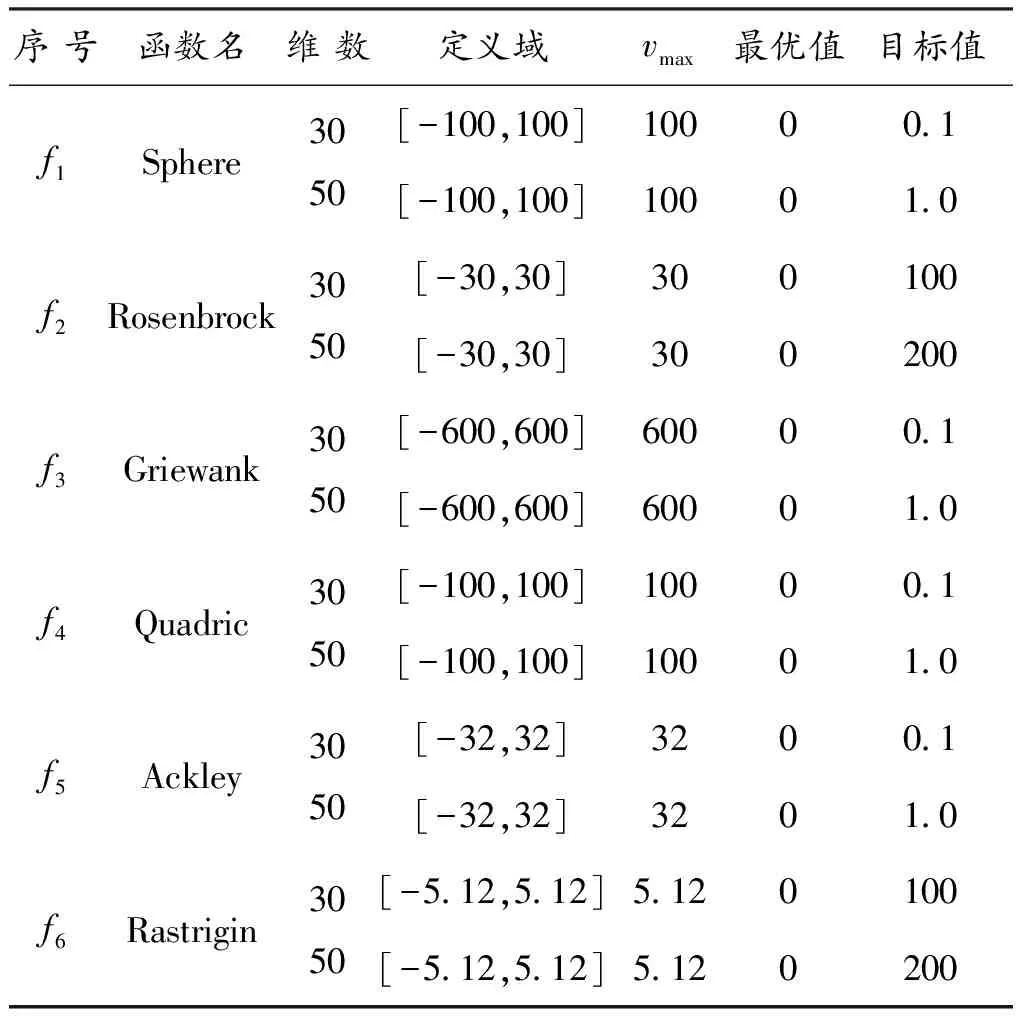
表2 标准Benchmark测试函数参数设置

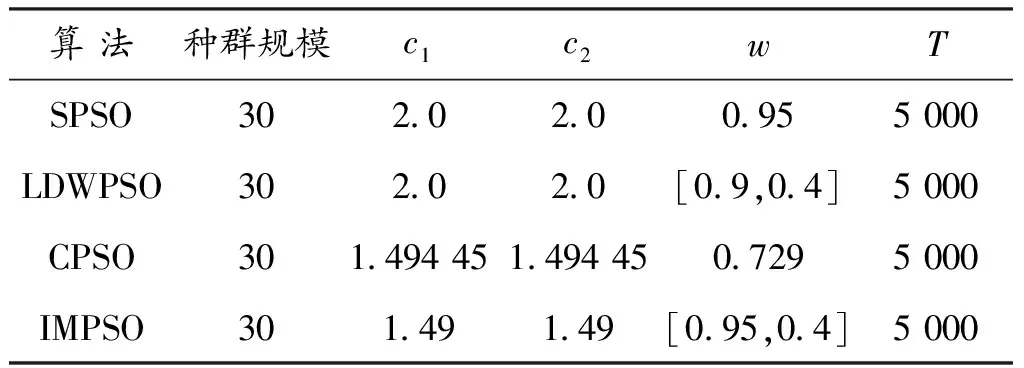
表3 各种算法的参数设置

由于篇幅有限，图1—图6给出了当维数D=30时该6个测试函数的平均最优适应度值随迭代次数的进化曲线。6个测试函数情况如式(8)—式(13)所示。

图1 f1测试函数

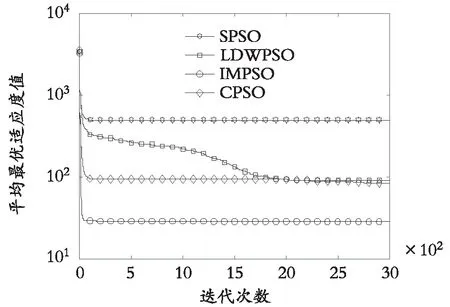
图2 f2测试函数

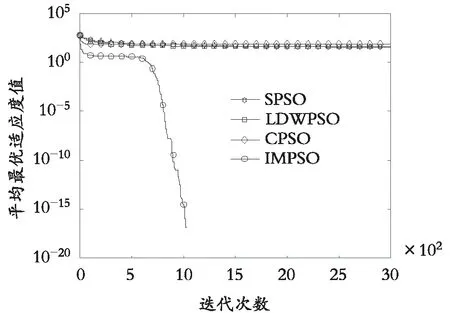
图3 f3测试函数

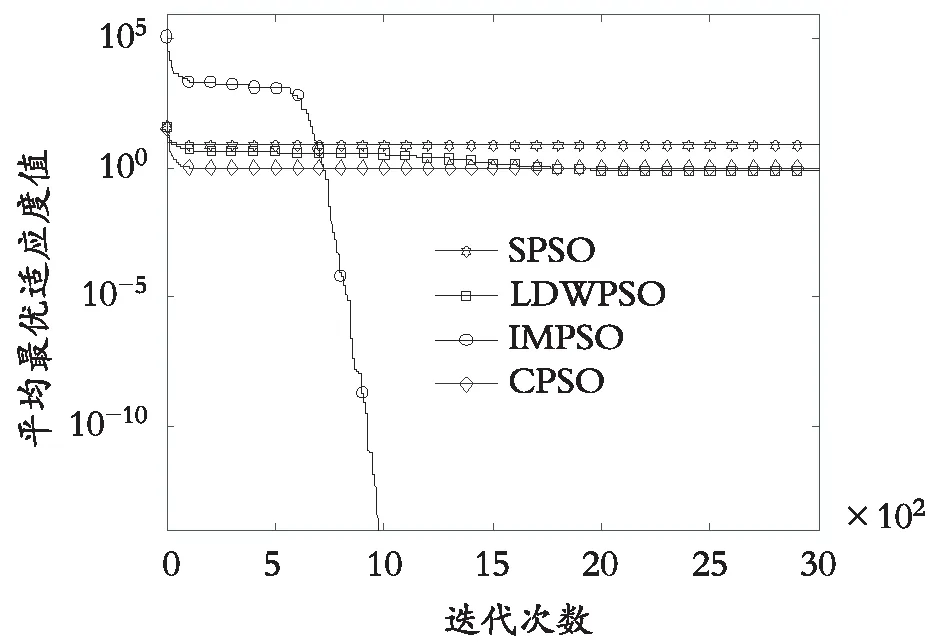
图4 f4测试函数

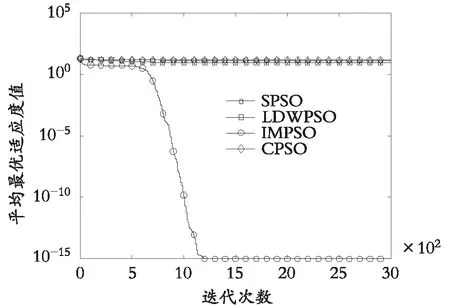
图5 f5测试函数

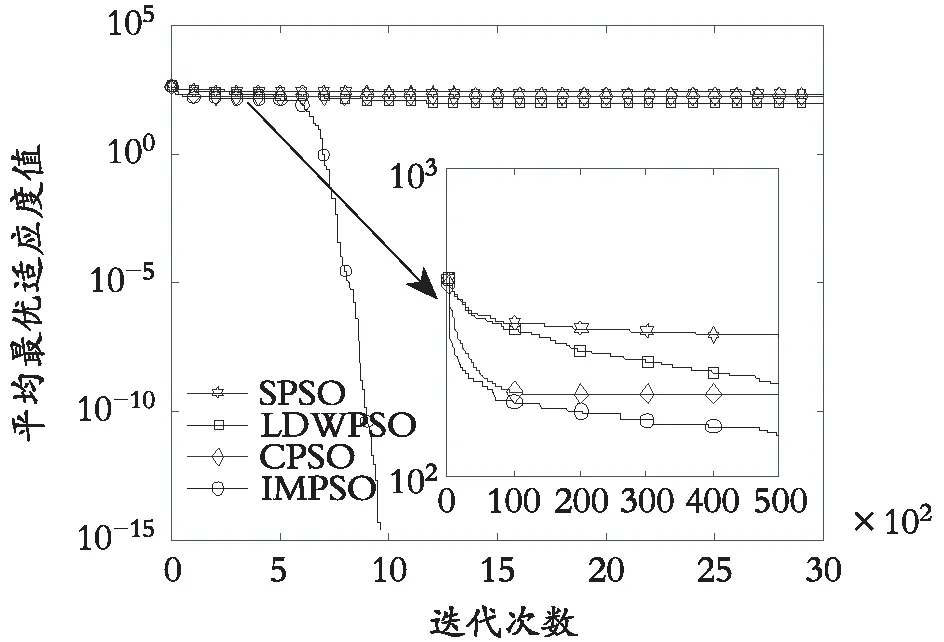
图6 f6测试函数

Sphere函数:

(8)

该函数是一个典型的单峰函数，在解空间上仅有一个极值点，当xi=0(i=1,2…)时取全局极小值0。

Rosenbrock函数:

(9)

该函数是一个非凸的病态多峰函数，虽然在解空间上有一个最小值点，但一般算法很难寻到最优解，其全局极小值位于一个平滑且狭长的抛物线形山谷内。当xi=1(i=1,2…)时取全局极小值0。

Griewank函数:

(10)

该函数是一个多峰函数，存在许多局部极小值点，是一种典型的非线性多模态函数，当xi=0(i=1,2…)时取全局极小值0。

Quadric函数:

(11)

该函数是一个单峰函数，当xi=0(i=1,2…)时取全局极小值0。

Ackley函数:

(12)

该函数是一个多峰函数，当xi=0(i=1,2…)时取全局极小值0。

Rastrigin函数:

(13)

该函数是一个多峰函数，拥有大量局部极值点，也是一种典型的非线性多模态函数，当xi=0(i=1,2…)时取全局极小值0。

算法性能评估指标采用如下方法:固定进化最优目标值，评估算法达到最优目标值的成功率(Success Rate，SR)，评估方式为算法达到最优目标值次数与算法执行总次数的比值；固定进化代数，评估算法收敛时的平均迭代次数(Average Iteration Times，AIT)，以反映算法的收敛性能。本文认为算法所寻得的最优值在连续2 000次迭代过程中没有变化时，即认为算法进入了收敛状态；固定进化代数，评估20次试验所得最优解的平均值(Mean)与最优解的标准方差(Std)，以反映算法的搜索性能与搜索精度。

4.3 实验结果及分析

表4列出了不同算法在6个测试函数中的性能指标，表5与表6分别给出了固定进化代数下求解6个测试函数时上述4种对比算法的最优值、平均最优值与最优值方差结果。其中，“-”表示对应算法在迭代过程中未达到收敛条件，即在固定进化代数内该算法不能收敛。可以看出，所提出的MPSO算法与其他3种算法在收敛性能与搜索精度上有着显著的差异，具体表现在:

(1)当测试函数为30维时，根据表4所列出的数据，对于上述全体测试函数，IMPSO算法的成功率都是100%，而不管对于单峰函数f1、f4还是多峰函数f2、f3、f5、f6，算法SPSO均未能达到理想目标值，成功率都是0。算法LDWPSO与算法CPSO在测试函数f1实验中的成功率分别为0和10%，在测试函数f2实验中的成功率分别为70%和90%，对于测试函数f3、f4、f5而言，这两种算法也均未能达到理想目标值，其成功率均为0。对于具有大量局部极值点的测试函数f6而言，算法LDWPSO的成功率超过了50%，而算法CPSO则表现出成功率为0，但都次于算法IMPSO在每个测试函数实验中所取得的成功率。结合测试函数为50维时的算法性能指标数据，能进一步地说明IMPSO算法不管是在单峰函数求解过程中，还是多峰高维函数求解过程中，其均能表现出自身的稳定性优势。

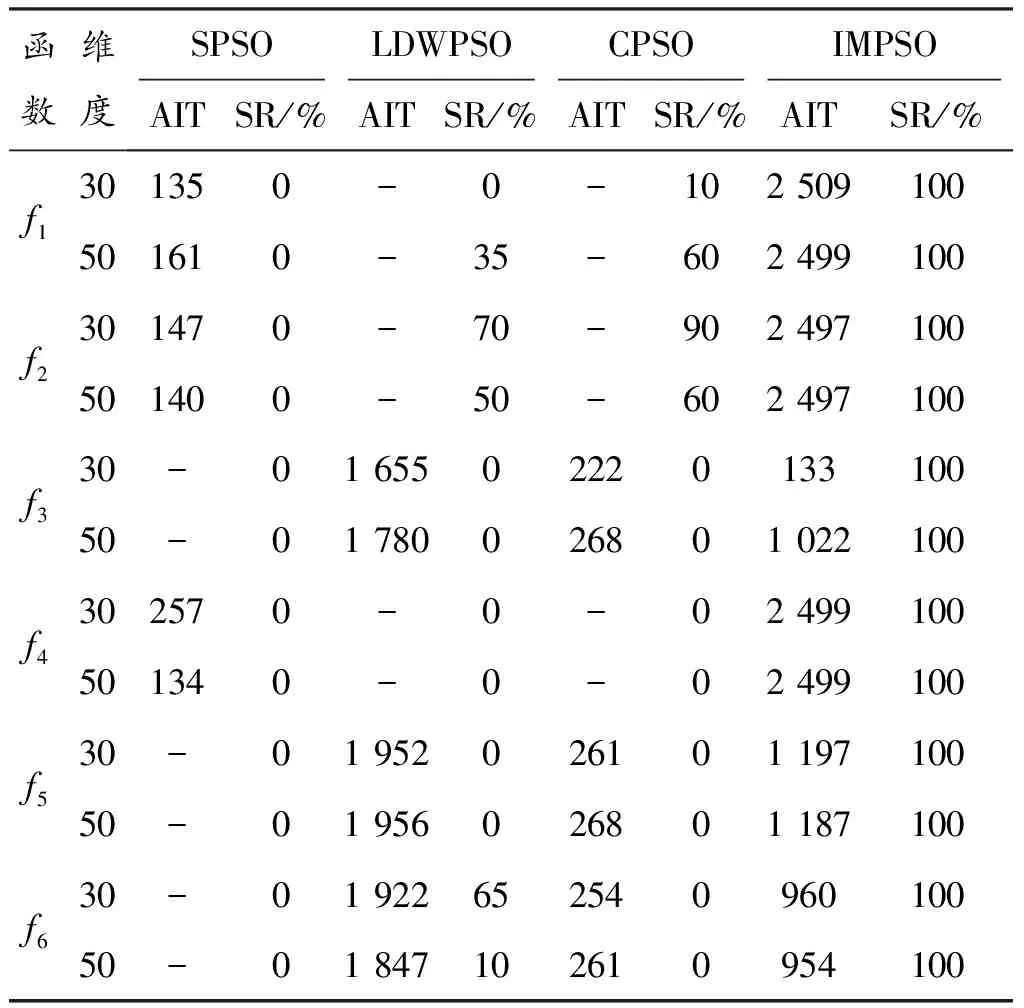
表4 各优化算法对每个测试函数的性能测试指标

(2)根据表5、表6可知：无论测试函数是30维还是50维，对于多峰函数f3、f6而言，算法IMPSO在每次进化过程中均能搜索到全局极小值点，比实验所设定的理想目标值精度更高，而算法SPSO、LDWPSO、CPSO在多峰函数f3测试中，均未能达到理想目标值，对于多峰函数f6，只有算法LDWPSO能在不同维度的解空间中搜索到理想目标值，但其成功率不高，分别为10%、65%。对于单峰函数f1、f4，算法IMPSO在解空间中搜索到的最优值对比于另外3种算法，差异更是明显，且IMPSO算法在不同维度解空间中最优值的标准方差远远小于另外3种算法，这也反映了IMPSO算法在单峰高维函数中的稳定性。对于多峰函数f2和f5，算法IMPSO所搜索到的最优解精度也远远高于其他三种算法。结合上述可看出，IMPSO算法具有更优越的全局寻优能力。

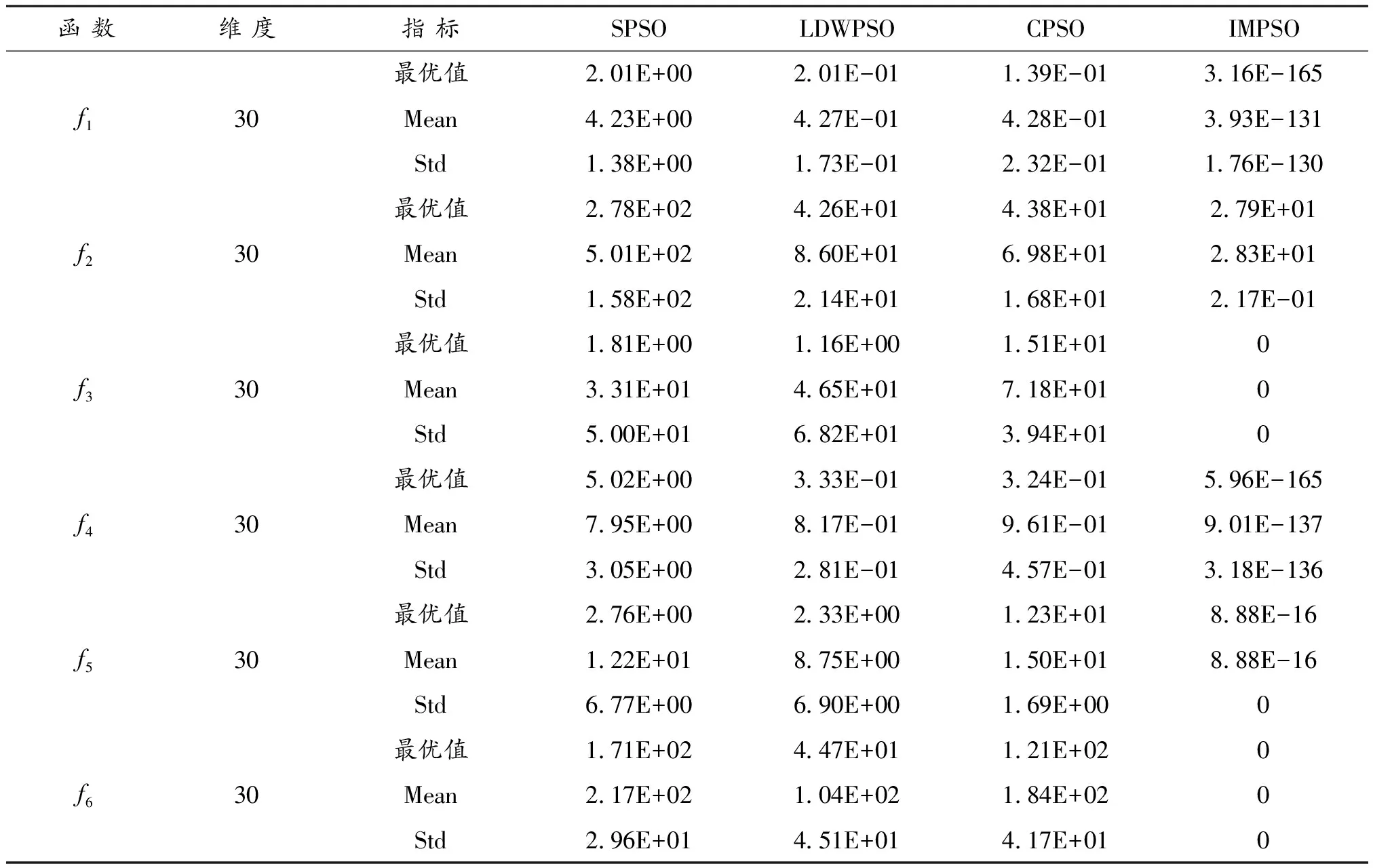
表5 30维时各优化算法对每个测试函数的实验结果

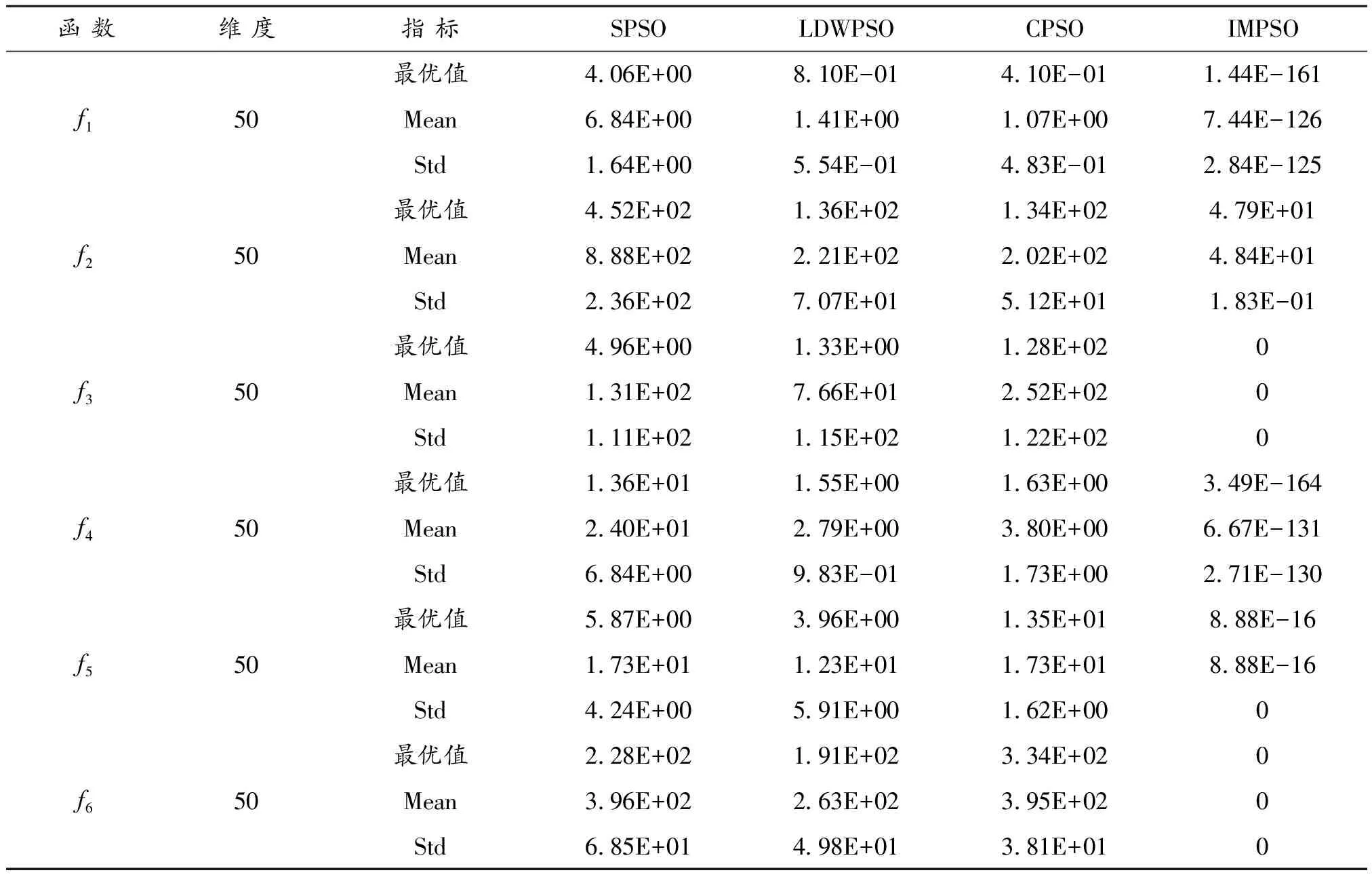
表6 50维时各优化算法对每个测试函数的实验结果

(3)根据表4所列出的AIT数据，结合图1—图6 所给出的不同算法在不同测试函数中平均最优值进化曲线，可明显地看出，除了在单峰函数f1与f4测试中，算法IMPSO在前期收敛速度慢于其他3种算法外，在其他4种测试函数中，算法IMPSO收敛速度均要优于另外3种算法且均能进入收敛状态，而另外3种算法在不同测试函数中都有表现出不收敛或者过早陷入局部最优值而达到收敛的情形。

(4)从图1—图6可以看出：除了多峰函数f2对应的平均最优值进化曲线在前500次迭代范围时收敛速度最快外，其余五组测试函数的收敛速度均在迭代次数超过500次后才开始进入快速收敛状态，这是因为当种群进化代数至500次时，种群粒子的惯性权值开始发生明显的非线性递减变化，对应的粒子将进行精细化搜索状态，从而快速地靠近最优值附近。而不同的测试函数，算法在其解空间内进行搜索时都具有一定的随机性与动态性。

从实验结果表4—表6和图1—图6可以看出：IMPSO算法在多峰、高维的空间中测试时，其优化性能要优于另外3种经典算法，但在单峰、高维的空间中测试时，所提算法也存在前期搜索速度较慢的缺陷。

5 结束语

在参照现有粒子群算法参数时变策略的基础上，针对粒子群算法出现的早熟收敛和不收敛的问题，提出了一种基于自然选择和惯性权值非线性递减变化策略的改进粒子群算法，并提出了粒子最大速度非线性递减策略，使得算法有较好的全局搜索与局部搜索的平衡能力。考虑种群多样性对粒子收敛性能的提高有较大影响，采用二阶振荡策略来保证算法收敛性能的同时，能够在进化过程中有效地提高种群的多样性。为提高粒子群算法局部精细寻优的能力与适用性，在算法中引入自然选择机理，这也符合无免费午餐定理，有效地提高了算法的鲁棒性，使得算法具有更好的全局寻优能力。通过与其他算法在测试函数上的寻优分析对比，实验结果表明，所提出的改进算法能够解决基本粒子群算法在求解高维复杂多峰非线性优化问题时出现的容易陷入局部最优值以及不收敛的问题。

参考文献(References):

[1] KENNEDY J，EBERHART R C.Particle Swarm Optimization[C]//Proc of IEEE Inernational Conference on Neural Networks,Piscataway:IEEE Service Center,1995:1942—1948

[2] AMR M I，NOHA H E.Particle Swarm Optimization Trained Recurrent Neural Network for Voltage Instability Prediction[J].Journal of Electrical Systems and Information Technology,2018(10):216—228

[3] DIEU T B，QUANG T B.A Hybrid Artificial Intelligence Approach Using GIS-based Neural-fuzzy Inference System and Particle Swarm Optimization for Forest Firesusceptibility Modeling at A Tropical Area[J].Agricultural and Forest Meteorology,2017(4):32—44

[4] SHI Y，EBERHART R C.Parameter Selection in Particle Swarm Optimization[C]//Proc of 7th International Conference on Evolutionary Programming Vii,Berlin:Springer-Verlag Press,1998:591—600

[5] SHI Y，EBERHART R C.A Modified Particle Swarm Optimizer[C]//Proc of IEEE International Conference on Evolutionary Computation,Piscataway:IEEE Press,1998:69—73

[6] 王永骥，苏婷婷,刘磊.基于柯西变异的多策略协同进化粒子群算法[J].系统仿真学报，2018,30(8):2875—2883

WANG Y J，SU T T，LIU L.Multi-strategy Cooperative Evolutionary PSO Based on Cauchy Mutation Strategy[J].Journal of System Simulation,2018,30(8):2875—2883(in Chinese)

[7] 贾会群，魏仲慧,何昕,等.基于改进粒子群算法的路劲规划[J].农业机械学报，2018,49(12):372—377

JIA H Q，WEI Z H，HE X，et al.Path Planning Based on Improved Particle Swarm Optimization Algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(12):372—377(in Chinese)

[8] 马国庆，李瑞峰，刘丽.学习因子和时间因子随权重调整的粒子群算法[J].计算机应用研究，2014,31(11):3292—3294

MA G Q，LI R F，LIU L.Particle Swarm Optimization Algorithm of learning Factors and Time Factor Adjusting to Weights[J].Application Research of Computers,2014,31(11):3292—3294(in Chinese)

[9] CLERC M，KENNEDY J.The Particle Swarm:Explosion,Stability and Convergence in A Multidimensional Complex Space[J].IEEE trans on Systems Man and Cybernetics,2002(6):58—73

[10] CLERC M.The Swarm and the Queen:Towards A Deterministic and Adaptation in Particle Swarm Optimization[C]//Proc of the 1999 Congress on Evolutionary Computation,Washington:IEEE Press,1999:1951—1957

[11] 龚纯，王正林.精通Matlab最优化计算[M].北京:电子工业出版社，2009:296—299

GONG C,WANG Z L.Optimal Calculation by Matlab[M].Beijing:Electronic Industry Press,2009(in Chinese)

[12] 胡建秀，曾建潮.二阶振荡微粒群算法[J].系统仿真学报,2007,19(5):997—999

HU J X，ZENG J C.Two-order Oscillating Particle Swarm Optimization[J].Journal of System Simulation,2007,19(5):997—999(in Chinese)

[13] 方群，徐青.基于改进粒子群算法的无人机三维航迹规划[J].西北工业大学学报，2017,35(1):67—68

FANG Q，XU Q.3D Route Planning for UAV Based on Improved PSO Algorithm[J].Journal of Northwestern Polytechnical University,2017,35(1):67—68(in Chinese)