具有ReLU函数的动力神经场方程稳定解的存在性
秦子雁,陈芃合,金德泉
(广西大学 数学与信息科学学院, 广西 南宁 530004)
0 引言
“动力神经场是皮层神经元群活动动态的平均描述” 这一观点在20世纪70年代被提出[1]。基于这一思想,涌现了很多关于动力神经场的方法和模型,并在优化、数据估计等方面得到了越来越广泛的应用[2-3]。在这些模型中,Amari的动力神经场方程是一个重要模型,因为它在不需要过多数学技巧的情况下就可以对其动态特性进行分析处理。因此,该模型被广泛应用于机器学习、关联记忆等诸多领域[4-5]。
由于动力神经场的相关研究主要依赖于其稳定性,因此研究稳态解的存在条件和动力学性质具有十分重要的意义。在一般研究的动力神经场研究中,阈值函数θ应该是单调且有界的,因此,Amari动力神经场的阈值函数多为传统的阶跃函数或Sigmoid型函数[6-7]。然而,当多个神经场相互耦合时,阶跃函数和sigmoid型函数的梯度可能会消失,这意味着当输入达到一定强度时,无论输入如何变化,都会出现相同的激活区域。由于ReLU激活函数具有较高的收敛速度和良好的逼近性[8],可以很容易地解决深度学习中高层结构的梯度消失问题,因此,ReLU函数在神经网络研究中越来越受欢迎[9-10]。而在动力神经场中,经常用DoG(differential of Gaussian)函数作为相互作用核,但是DoG函数的参数较多,使得相应的动力学性质难以解释,而高斯函数在参数相对少的情况下具有相似的性质。
笔者主要讨论在一维空间中,以ReLU函数作为阈值函数,高斯函数作为相互作用核的Amari动力神经场方程中的稳定解的存在条件和相关结论。
1 预备知识
一维的Amari动力神经场方程[11]为
(1)
τ为大于0的时间常数,v(x,t)表示在感知场中,当时间为t时,位于x的神经元活性,Ω为感知区域,s(x,t)是输入信息的分布函数,h为动力神经场的静息水平,也称静息电位。θ(v)是单调递增阈值函数,用来描述神经元在神经场内的兴奋情况。令{x∈Ω:v(x,t)>0}为兴奋域,假设动力神经场无外部输入,即s(x,t)=0,且有初始状态v(x,0)=v0(x),则一维的Amari动力神经场方程可以改写为
(2)
阈值函数θ(v)取ReLU函数。
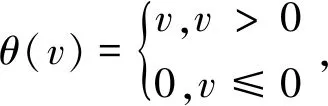
(3)
与传统的阶跃函数或Sigmoid型函数不同,ReLU函数是单调递增但是无上界的。它打破了当θ(v)是一个阶跃函数,只有激活神经元才产生相互反馈的力量,且相互作用力度是完全由相互作用核定义的这一规律,使得在静息状态下被激活的神经元也可能对其他神经元产生反馈,且反馈力度与阈下刺激程度相关。
w(x,x′)为动力神经场的相互作用核,由于相互作用核通常是各项同性的,所以也可以写成w(x-x′)。相互作用核通常具有“墨西哥帽”形[12]。取w(x)为高斯函数,即
(4)
其中相互作用尺度σ>0,且满足
(5)
定义若v*(x)为神经场方程的稳定解[1,13],即
(6)
则有
(7)
① 若∀x∈R,v*(x)≤0,则称v*(x)为Amari动力神经场的φ解;
② 若∀x∈R,v*(x)>0,则称v*(x)为Amari动力神经场的∞解;
③ 若有a1,a2∈R,当x∈(a1,a2)时,v*(x)>0;当x∉(a1,a2)时,v*(x)≤0,则v*(x)为Amari动力神经场的a解。
若动力神经场只存在φ解,表示动力神经场不存在兴奋域,若只存在∞解则表示动力神经场在感知区域Ω内全局兴奋,若只存在a解则表示存在感知区域Ω内存在局部兴奋域。
2 主要结果
令相互作用核w(x,x′)满足式(5),则有:
命题1①若h<0,则有v*(x)=h为动力神经场式(2)的唯一φ解。
② 若动力神经场存在一个φ解,则h≤0。
证明∀x∈R,有v*(x)=h,且h<0,则有θ(v)=0。故式(2)右边项可以写成
(8)
故v*(x)=h为式(2)的φ解。
下证稳定解唯一,若∀x∈R,假设有另一φ解v*(x)=h1≠h,则h1<0,θ(v)=0。故式(2)右边项可以写成
(9)
即h1=h,与假设矛盾,φ解唯一得证。
若动力神经场存在一个φ解v*(x),则有v*(x)≤0,θ(v*)=0。故有
(10)
由v*(x)≤0,v*(x)=h,故h≤0,证毕。
由上可得,h<0 是φ解存在的充分条件及必要条件,同时,动力神经场内有且只有一个φ解。这表明在给定动力神经场方程为式(2),无外部输入时,只有当静息水平为负,动力神经场的稳态解中才不会使得感知区域中出现兴奋域。此时感知区域内的所有神经元均不能被激活。全局抑制性质对动力神经场应用在机器学习及工程上具有重要意义,它从理论上保证了动力神经场不存在全局兴奋区域。这意味着,只要保持h<0,便可以适当地调整参数,使得动力神经场感知区域从无兴奋域变成局部兴奋但不会出现全局兴奋,可以更自由地应用在机器学习和工程中。
命题2①当h>0时,动力神经场方程(2)的所有稳定解均为∞解。
② 若动力神经场存在一个∞解v*(x)∈[0,1],则有W∞+h>0。
证明当h>0时,有稳定解v*(x), 由阈值函数公式,θ(v*(x))≥0,则
(11)
由v*(x)≥h,h>0得v*(x)>0。 故动力神经场所有稳态解均为∞解得证。
有稳定解v*(x)∈[0,1], 由阈值函数公式,θ(v*(x))∈[0,1], 则有
(12)
由v*(x)>0,v*(x)≤W∞+h得W∞+h>0,证毕。
命题2得出了∞解存在的相关条件。通常来说,在机器学习、数据挖掘和工程应用中应该规避∞解,因为∞解代表感知区域内全局兴奋。在给定动力神经场方程为式(2)的情况下,当h>0时,动力神经场所有的稳定解均有感知区域全局兴奋,这可以推断出,在有外部输入的情况下,当h>0时,任何正向的外部刺激对于动力神经场均无差别。此时,动力神经场无法从外部输入刺激中学习和提取刺激相关的特征和信息。
若有∞解v*(x)上界为b(b>0),则有θ(v*(x))≤b。
(13)
因此,命题2给出了在无外部输入的情况下,规避动力神经场∞解的静息水平指标,即在动力神经场的方程为(2)式的情况下,静息水平应有h≤0;在无外部输入且有上界为b(b>0)的情况下, 规避动力神经场(2)式∞解的静息水平指标应为bW∞+h≤0。
命题3若存在一个a解,当x∈(a1,a2)有 0≤v*(x)
证明若∀x∉(a1,a2),v*(x)≤0 则有阈值函数θ(v)=0,由式(7),则
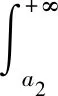
(14)
所以,由v*(x)≤0,v*(x)≥h, 得h≤0。
若∀x∈(a1,a2),0≤v*(x) (15) 所以,由v*(x)>0,v*(x) 由上可知,bW∞+h>0及h≤0是上界为b的动力神经场a解存在的充分条件,这是表明在符合以上条件且没有外界刺激的情况下,动态神经场可以保持(a1,a2)为兴奋域作为短期记忆。当阈下刺激增大时,局部兴奋的区域也增大,当不同神经场相互耦合时,兴奋域可以相互叠加,可以用来模拟同一区域对于不同刺激的兴奋反应。WANG等[14]利用局部兴奋和全局抑制,即全局无兴奋域,在震荡神经网络中模拟人的感知突现,随后与深度学习结合用来解决“鸡尾酒会问题”,进行语音的分离和降噪。陈薇薇等[15]在利用全局抑制核局部兴奋机制的神经元震荡网络的基础上结合最小叉熵原理提出了参数自适应的新型图像分割方法,并运用在医学图像分割中。 本文讨论了一维Amari动力神经场方程稳定解的一些性质。与经典的Amari动力神经场不同的是,利用单调递增但是无界的ReLU函数作为阈值函数,高斯函数作为相互作用核,得到了Amari动力神经场的三种典型稳定解存在的相关条件与结论。当不考虑外部输入时,阈值函数无界时,稳定解的存在性与稳定解的界和静息水平的取值高度相关。本文对三种稳定解在认知、感知科学及机器学习中的应用的现实意义也进行了阐述。首先,可以实现全局抑制的φ解与局部兴奋相结合,有重大的现实意义,可以更加自由地运用在机器学习中;其次,提出了在无负向外部输入情况下规避∞解的静息水平指标;最后对a解和全局抑制在机器学习方面的应用进行了简要的说明。以上研究成果较为新颖,具有较高的理论价值,可以为动力神经场的理论研究和动力神经场在认知科学及机器学习的应用方面提供相应理论依据。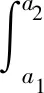
3 结论

