破解中考几何压轴题技巧探究

何军健

摘 要：几何压轴题常见于全国各地数学中考试卷。几何压轴题注重考查学生思维能力，难度比较高，对考生的几何知识基础掌握程度要求很高，同时需要学生具备一定的综合应用能力，学生要在有限时间内完成有一定难度，所以学生要快速找到解决压轴题的突破口还是需要一定技巧。因此文章主要对破解中考几何压轴题技巧进行探究，总结了“以问为导，寻找线索”“化繁为简，各个击破”“前后联动，融会贯通”三个破解技巧。

关键词：中考;几何压轴题;解题技巧

一、问题的提出

压轴——指一场折子戏演出的倒数第二个剧目。在考试中所说的压轴题是从这里引申过来的。很多数学考试通常把最有分量的试题放在最后三道题，也是我们所说的压轴题，这也是学生成绩拉开距离的题目，可见放在这些位置的题目无论是分值还是难度都不一般。每年的数学中考试后，说起中考压轴题，特别是几何压轴题，很多学生都说无从下手，或者有些会说：“题目我都没有看过……为什么会出现这种情况呢？难道压轴题真的是高不可攀的山峰吗？”

笔者任教毕业班多年，发现出现这种情况有客观原因也有主观原因。客观原因是我们都知道压轴题就是一张试卷里面比较难的题目，出题目的就是要区分出优等生和一般生，达到为高一级学校选拔人才的目的，所以压轴题难度比较高，主要考查学生的综合应用能力，学生要在有限时间内完成有一定难度;而主观原因是很多教师一开始就灌输：“压轴题很难的，考试时间不多，把多点时间放在检查前面已经完成的题目，保证正确率。”人为地给学生营造恐惧心理，让很多学生谈题色变，以至在考试过程中很多学生都放弃压轴题。如何让学生突破压轴题这个瓶颈呢？笔者认为在平常的教学中要教会学生破解压轴题的技巧。

二、技巧的概念界定

技巧，指表现在文学、工艺、体育等方面的巧妙的技能。如“谈话技巧”;或者指技巧性的运动。如“技巧比赛”。技巧也可以说是属于“方法”的一个范畴，主要指对一种生活或工作方法的熟练和灵活运用，也可比喻解决问题的好办法。而数学解题技巧是指根据有关数学问题的不同特性，总结归纳出的巧妙的解题好方法与技能，帮助学生准确快速地找到解题思路，化难为简，提升驾驭数学的能力，最终达到解题目的。

美国数学家哈尔莫斯指出：“问题是数学的心脏，数学家存在的理由就是解问题。因此，数学的真正的组成部分是问题和解。”数学家G·波利亚曾说过，“掌握数学就意味着善于解题”。他长期致力于“怎样解题”的研究，他指出：“掌握数学就是意味着善于解题，不仅善于解一些标准的题，而且要善于解一些要求独立思考、思路合理、见解独到和有发明创造的题。”法国著名数学家阿达玛在其名著《数学领域中的发明心理学》把学生的解题过程与数学家的发明创造相提并论：“一个学生解决某一代数或几何问题的过程与数学家做出发现或创造的过程具有相同的性质，至多只有程度上的差异。”因此中学数学教育首要任务就是加强解题训练，教会学生思考，引导学生发现总结题目的解法和技巧，提高解题能力。

三、破解中考几何压轴题技巧的探究

对于中考几何压轴题的研究，每年都有不少文章针对当年全国各地最新的中考几何压轴题进行破解，国内不少学者也对破解中考几何压轴题的常用方法进行研究，取得不同程度的效果。但是众所周知，中考压轴大题都是出题老师的心血结晶，不会重复出现题目，思路也是做过多少套模拟题都没有遇到过的新型题目，或者是之前碰到过一个类似的题型。可见中考压轴题设计的可变性，每一道题的设计都不是一成不变的，那么是否可以找到一些方法或技巧去解决变化的中考幾何压轴题？笔者认为不管题目如何变化，总能找到一些破解中考几何压轴题的通用技巧。笔者经过多年的毕业班教学实践，对破解中考几何压轴题技巧进行研究，总结了如下三个破解技巧。

（一）以问为导，寻找线索

对于中考压轴题，很多学生听到“压轴”二字就害怕，以为一点都不会做，其实压轴题并不是竞赛题，只是综合性及创新性更强。一般地，中考数学压轴题通常有三个小问，其中第一问比较简单，中等水平的学生能够比较轻易地解出来;第二问通常有些难度，通常要利用第一问的条件和结论。所以解决这一问可以用“以问为导，寻找线索”的方法解决。

我们知道所有题目设计的条件中有明显和隐含的，而所有的条件都是为问题而设计的，所以我们要快速判断出所给条件为谁服务，则要明白服务对象是谁。因此笔者认为破解压轴题也一样，特别是解决压轴题第一问，可以先了解问题，后带着问题看题目，寻找解题的线索，这样可以达到事半功倍的效果。

如：（2015·陕西中考）如图，在每一个四边形ABCD中，均有AD∥BC，CD⊥BC，∠ABC=60°，AD=8，BC=12.

（1）如图①，点M是四边形ABCD边AD上的一点，则△BMC的面积为____________________;

（2）如图②，点N是四边形ABCD边AD上的任意一点，请你求出△BNC周长的最小值;

（3）如图③，在四边形ABCD的边AD上，是否存在一点P，使得cos∠BPC的值最小？若存在，求出此时cos∠BPC的值;若不存在，请说明理由。

分析：此题属于四边形综合题，涉及的知识有：勾股定理，矩形的判定与性质，对称的性质，圆的切线的判定与性质，以及锐角三角函数定义，考查的知识点比较多。如何快速解答这道题呢？若直接读题目，虽然题目文字不多，有好几个明显条件，但是所给条件与什么问题匹配？一下子是判断不出来的，但若我们先看问题再回头看题目，就基本可以判断条件的作用。例如第一问，问题是求△BMC的面积，那么按照求三角形面积公式：[12]底边×高，要解决这个问题，就要找到对应的底边和高。所以回头看题目就知道底边BC是已知，没有给出高，需要求高。又比如第二问，要求△BNC周长的最小值，要解决这个问题则需要知道各边长，所以看题目就会留意要看是否给出与此三角形有关的线段长度。通过这样操作，明确解题的方向。

从以上例子我们可以看出，用“以问为导，寻找线索”的方法解决几何压轴题，既节省了时间，避免重复花时间阅读题目，又可以帮助学生快速找到问题所需要的条件和突破口，大大增加了得分概率。笔者认为教会学生这种解题思路，可以提高学生解决几何综合题的能力，特别是对于很多学习程度中下的学生来说是提高解决综合题第一问的能力的一个好方法。

（二）化繁为简，各个击破

几何综合题大多是平行线、三角形、四边形、相似三角形、锐角三角函数、圆等知识的综合运用，考查知识点多、图形复杂且条件隐晦，难度较高，要求学生有较强的理解能力、分析能力、解决问题的能力，数学基础知识、数学基本方法有较强的驾驭能力，并有较强的解题创新意识和能力。但是所有复杂的图形都是由基本图形构成的，所以，遇到图形复杂的几何综合题时可以尝试用“化繁为简，各个击破”的方法，通过重画图形，把复杂图形拆解回基本图形，逐步递进，识破命题意图，这样就能很清晰找到解题方法。

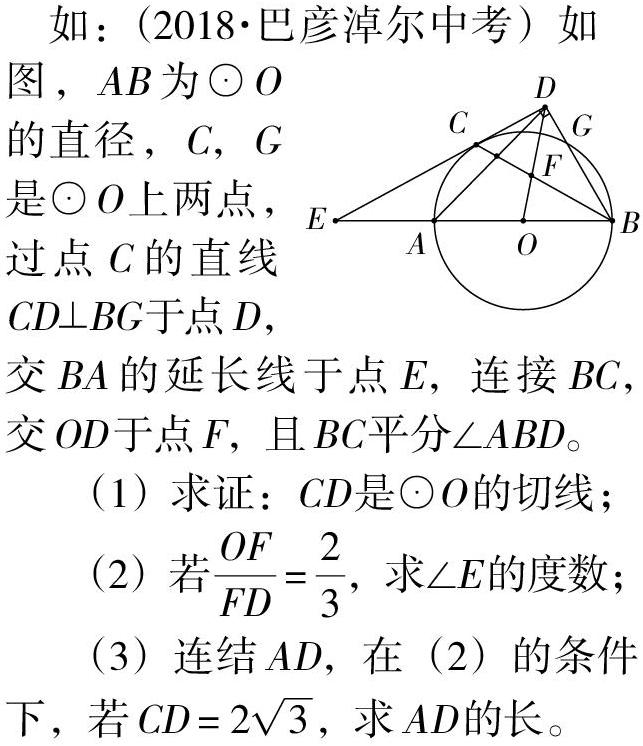
分析：本道题是一道圆综合题，重点考查切线的判定与性质、相似三角形的判定与性质、数形结合的思想等。题目文字不多，但是图形给学生的感觉比较复杂，线段错综复杂，容易给学生造成视觉混乱，给学生造成恐惧感。笔者认为压轴几何题的图形复杂是必然的，因为一道综合题要考察的知识点较多，知识点的构成靠众多具备某些特征的基本图形构成，所以它的图形必然复杂。那么如何破解呢？笔者经过多年毕业班教学实践及研究多年的中考几何压轴题，发现可以根据问题的逐步递进把图形拆解，我们可以重新画图，把一些不需要或没有用到的线先省去，简化图形，从而达到化繁为简，各个击破。

比如我们看第一问，它是求证CD是⊙O的切线，这一问实际上主要是与圆和线段CD有关，而线段OF、FD、AD及点G、A都没有涉及，我们可以重新画图，把这些线段及没有涉及的点省去，简化图形，如右图为简化后的图形。此图相对原图就简单明了，学生在平常都接触过，学生只要连接OC证OC⊥ED即可。证明过程如下：

至此，已经完成第一、第二问的解题，第三问才真正用到原图。一般第三问都是比较难的，况且分值也不多，这时在时间不多的情况下我们可以考虑放弃。

由以上例子可以发现，在遇到图形复杂的几何综合题时可以尝试化繁为简，各个击破，可以把原题图形做化繁为简处理，把还没有用到的点或线不画上去，简化图形，避免复杂的图形影响学生的思考，让学生快速、清晰地找到解题方法。

（三）前后联动，融会贯通

一般地，中考数学压轴题通常有三小问，压轴题三小问之间命制的模式有并列、递进或并列与递进混合的逻辑关系，也就是有些压轴题各小问是并列关系（即各问之间是独立关系），有些是递进关系（即第一问为第二问服务，第二问又为第三问服务，有些第一、第二问都为第三问服务），有些是并列与递进混合关系。压轴题第一问比较简单，中等水平的学生能够比较轻易地解出来。所以，看到压轴题，学生不要过于恐惧，拿下第一问还能得两三分。第二问通常有些难度，通常要利用第一问的条件和结论，所以，如果第一问做不出来，后面就更难。第三问难度最大，考验的是学生的综合能力。所以解答压轴题还有一个技巧就是注意三小问之间的逻辑关系，判断出它们的逻辑关系，捕捉命题者思路，然后前后联动，融会贯通，快速找到解题方法。

如：（2017·南充中考）如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF=[14]AB。

（1）求证：EF⊥AG;

（2）若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？

（3）正方形ABCD的边长为4，P是正方形ABCD内一点，当S△PAB=S△OAB，求△PAB周长的最小值.

分析：本题是四边形综合题目，综合性强，主要考查正方形的性质、相似三角形的判定与性质、勾股定理、三角形内角和定理、直角三角形的性质等知识。本题文字不多，图形也不算复杂，我们如何快速找到思路去解决呢？笔者认为可以用“前后联动，融会贯通”的方法去找到突破口。

首先看问题，发现第一、第二问的问题都是证明EF⊥AG，而第三问由面积去求周长，可以猜想本道题整个逻辑关系基本上是递进关系或部分是递进关系，所以关键是要解决第一问，解决不了第一问，估计第二、第三问有一定的难度，所以突破口在第一问。解答过程如下：

由于第一问是证明特殊位置的结论，第二问是探索运动情况下第一问的结论是否成立，根据递进关系，猜想第二问的判定证明思路和方法可以模仿第一问去做，实际第一问的解决方法对第二问有提示作用，这样就很容易解决了第二问，看具体证明过程：

（2）解：成立;理由如下：

以上例子说明，我们在做几何压轴题时可以由命题者设计的三个问题的逻辑关系，通过前后联动，融会贯通，快速找到相应解决问题的突破口。

四、结束语

几何压轴题作为考查考生思维能力的一个重要方面，在中考中仍占有相当的比例。以几何重点知识为载体，要求考生根据题意设计有一定层次、一定长度的推理过程，以检测考生的逻辑思维能力、基本图形分析能力和数学语言的表达能力，仍是中考命题的重点之一，几何压轴题对考生的知识基础掌握程度要求很高，学生需要一定的思维能力，但是要能快速找到解决压轴题的突破口还是需要一定技巧的。根据多年任教毕业班和教学实踐经验，笔者总结出破解中考几何压轴题的三个通用技巧，目的在于遇到几何压轴题时，为学生快速找到解题思路，化难为简，提升驾驭数学的能力，最终达到解题目的。

（广东省茂名市崇文学校，茂名525000）